аналитическая (от греч. analytikos - расчлененный) форма. Составная форма, образуемая сочетанием служебного и знаменательного слов (ср.: синтетическая форма). Аналитическая форма сравнительной степени прилагательных. Более красивый. Аналитическая форма превосходной степени прилагательных. Самый красивый. Аналитическая форма будущего времени. Буду делать.

Составить слова из слова аналитическая

Аналити́ческая геоме́трия - раздел геометрии, в котором свойства геометрических образов (точек, линий, поверхностей) устанавливаются средствами алгебры при помощи метода координат, то есть путём изучения свойств уравнений, графиками которых эти образы являются. В аналитической геометрии исследуются линии (поверхности) 1-го и 2-го порядков. Линии (поверхности) 1-го порядка - прямые (плоскости); среди линий (поверхностей) 2-го порядка - эллипсы, гиперболы, параболы (эллипсоиды, гиперболоиды, параболоиды). Аналитическую геометрию впервые изложил в 1-й половине XVII в. Р. Декарт.

* * *

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ - АНАЛИТИ́ЧЕСКАЯ ГЕОМЕ́ТРИЯ, раздел геометрии, в котором свойства геометрических образов (точек, линий, поверхностей) устанавливаются средствами алгебры при помощи метода координат, т. е. путем изучения свойств уравнений, графиками которых эти образы являются. В аналитической геометрии исследуются линии (поверхности) 1-го и 2-го порядков. Линии (поверхности) 1-го порядка - прямые (плоскости); среди линий (поверхностей) 2-го порядка - эллипсы, гиперболы, параболы (эллипсоиды, гиперболоиды, параболоиды). Аналитическую геометрию впервые изложил в 1-й пол. 17 в. Р. Декарт.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ - раздел геометрии, в котором свойства геометрических образов (точек, линий, поверхностей) устанавливаются средствами алгебры при помощи метода координат, т. е. путем изучения свойств уравнений, графиками которых эти образы являются. В аналитической геометрии исследуются линии (поверхности) 1-го и 2-го порядков. Линии (поверхности) 1-го порядка - прямые (плоскости); среди линий (поверхностей) 2-го порядка - эллипсы, гиперболы, параболы (эллипсоиды, гиперболоиды, параболоиды). Аналитическую геометрию впервые изложил в 1-й пол. 17 в. Р. Декарт.

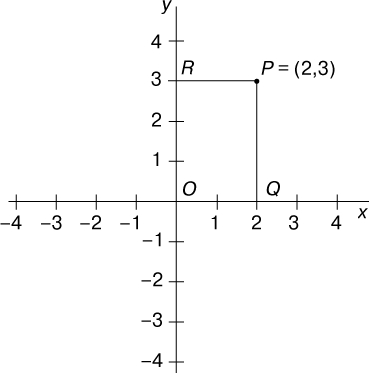
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ - раздел геометрии, который исследует простейшие геометрические объекты средствами элементарной алгебры на основе метода координат. Создание аналитической геометрии обычно приписывают Р.Декарту, изложившему ее основы в последней главе своего трактата Рассуждение о методе, озаглавленной Геометрия (1637). Однако сам метод был известен П.Ферма еще в 1629, о чем свидетельствует его переписка. Аналитическая геометрия стала неоценимым подспорьем для математического анализа, изобретенного вскоре Ньютоном (1665-1666) и Лейбницем (1675-1676). Методы аналитической геометрии применимы к фигурам на плоскости и к поверхностям в трехмерном пространстве, а также допускают естественное обобщение и на пространства более высоких размерностей. Мы начнем с аналитической геометрии на плоскости. Сущность метода координат состоит в следующем. На плоскости задаются две взаимно перпендикулярные прямые (координатные оси), пересекающиеся в точке О, называемой началом координат. Одна из них - ось x, или ось абсцисс, обычно выбирается горизонтальной, другая - ось y, или ось ординат, - вертикальной. Справа от O выбирается точка, у которой ставится отметка 1. Если принять отрезок от O до 1 за единицу длины, то откладывая последовательно этот отрезок вдоль прямой, мы получаем числовую ось. Считается, что эта ось продолжается вправо до бесконечности. Точки на оси x слева от O помечаются отрицательными числами, как на шкале термометра. Например, точка -2 расположена от точки O слева на таком же расстоянии, как точка 2 справа. Аналогичным образом с той же единицей длины размечается и ось y. Положительные числа располагаются выше точки O, отрицательные - ниже. Пусть P - любая точка на плоскости с заданной системой координат, Q - основание перпендикуляра, опущенного из P на ось x, а R - основание перпендикуляра, опущенного из P на ось y. Положение точки P полностью определяется двумя числами, называемыми координатами x и y. Первая координата указывает положение точки Q на оси x, вторая - положение точки R на оси y. На рис. 1 положение точки P полностью определяется ее координатами (2,3).

1. ДВЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ, называемые осью x и осью y, составляют основу для большинства операций в аналитической геометрии на плоскости. Именно они позволяют использовать алгебраические средства в геометрии и геометрические - в алгебре. Будучи снабженными шкалами, они представляют координаты точки. Например, точка P имеет координату x, равную 2, и координату y, равную 3.">

Рис. 1. ДВЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ, называемые осью x и осью y, составляют основу для большинства операций в аналитической геометрии на плоскости. Именно они позволяют использовать алгебраические средства в геометрии и геометрические - в алгебре. Будучи снабженными шкалами, они представляют координаты точки. Например, точка P имеет координату x, равную 2, и координату y, равную 3.

Основная задача аналитической геометрии заключается в изучении геометрических фигур с помощью соотношений между координатами точек, из которых эти фигуры образованы. Любую фигуру можно рассматривать как множество точек, удовлетворяющих некоторому геометрическому условию. Это условие можно записать в виде алгебраического уравнения, связывающего координаты x и y каждой точки фигуры. Суть метода аналитической геометрии состоит в изучении свойств фигуры с помощью соответствующего уравнения, исследуемого средствами алгебры. Этот метод позволяет устанавливать геометрические факты систематичным образом, в отличие от традиционной "синтетической" геометрии, где приходилось изобретать методы доказательства для каждого отдельного случая. Основным инструментом аналитической геометрии служит формула для вычисления расстояния между двумя точками P1 = (x1,y1) и P2 = (x2,y2). Числа x1, y1, x2 и y2 могут быть любыми действительными числами, положительными, отрицательными или 0. На рис. 2 все числа выбраны положительными. Проведем через точку P1 горизонтальную прямую, а через точку P2 - вертикальную. Пусть R - точка их пересечения. Тогда по теореме Пифагора

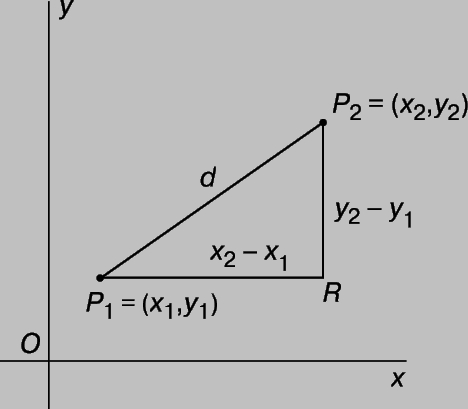
Рис. 2. РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ можно найти, если построить прямоугольный треугольник с катетами, параллельными осям координат. Расстояние между точками P1 и P2 устанавливается по теореме Пифагора.

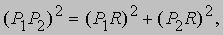
откуда d 2 = (x2 - x1)2 + (y2 - y1)2. Это и есть формула для вычисления расстояния между двумя точками. Важно иметь в виду, что эта формула остается в силе независимо от того, как расположены точки P1 и P2. Например, если точка P2 расположена ниже точки P1 и справа от нее, как на рис. 3, то отрезок RP2 можно считать равным y1 - y2, а не y2 - y1. Расстояние между точками, вычисляемое по формуле, от этого не изменится, так как (y1 - y2)2 = (y2 - y1)2. Заметим, что так как величина y2 в этом случае отрицательна, разность y1 - y2 больше, чем y1, как и должно быть.

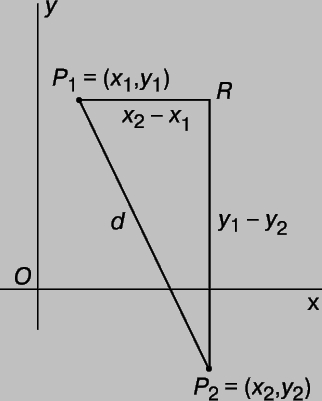
Рис. 3. ФОРМУЛА ДЛЯ ВЫЧИСЛЕНИЯ РАССТОЯНИЯ не изменяется, если одна из точек имеет отрицательные координаты, так как величина (y1 - y2)2 положительна, даже если величина (y1 - y2) отрицательна.

Прямые. Прямая - одна из простейших геометрических фигур. Алгебраическое уравнение прямой также имеет простой вид. Пусть B = (0,b)- точка пересечения прямой L с осью y, а P = (x,y) - любая другая точка на этой прямой. Проведем через точку B прямую, параллельную оси x, а через точку P - прямую, параллельную оси y; проведем также прямую x = 1. Пусть m - угловой коэффициент прямой L (см. рис. 4). Так как треугольники BSQ и BRP подобны, то

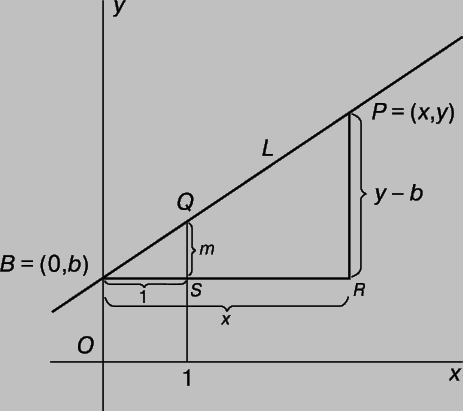
Рис. 4. ЛЮБАЯ НЕВЕРТИКАЛЬНАЯ ПРЯМАЯ, например L, определяется заданием точки, в которой она пересекает ось y (точка b) и угловым коэффициентом m, определяемым отношением (y - b)/x, или расстоянием QS по вертикали при x = 1.

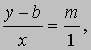
или, после упрощения,

Следовательно, если точка P лежит на прямой L, то ее координаты удовлетворяют уравнению (1). Обратно, нетрудно показать, что если x и y связаны между собой уравнением (1), то точка P непременно лежит на прямой L, проходящей через точку (0,b) и имеющей угловой коэффициент m. Таким образом, уравнение любой прямой можно записать в виде

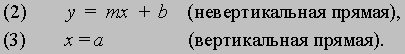
В обоих случаях мы получаем уравнение первой степени. Кроме того, каждое уравнение первой степени по x и y можно привести к виду (2) либо (3). Рассмотрим произвольное уравнение первой степени

Если B № 0, мы можем записать уравнение (4) в виде

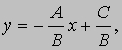
т.е. в виде (2). При B = 0 уравнение (4) сводится к уравнению Ax = C, или

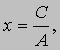
т.е. к уравнению вида (3). Таким образом, любая прямая описывается уравнением первой степени по x и y, и обратно, каждое уравнение первой степени по x и y соответствует некоторой прямой.

Парабола. Методы аналитической геометрии позволяют без особых трудностей исследовать свойства кривых, которые обычно не рассматриваются в стандартных учебниках планиметрии. Пусть заданы точка F с координатами (0,1) и прямая y = -1 (рис. 5). Множество точек P = (x,y), для которых расстояние PF равно расстоянию PD, называется параболой. Прямая y = -1 называется директрисой параболы, а точка F - фокусом параболы. Чтобы выяснить, как располагаются точки P, удовлетворяющие условию PF = PD, запишем его с помощью координат:

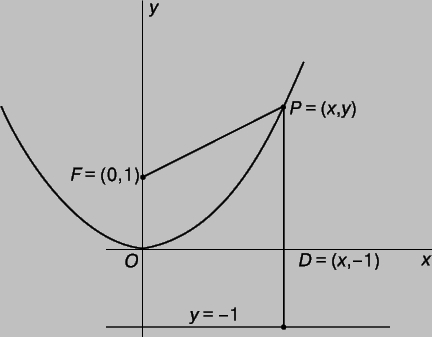
Рис. 5. ПОСТРОЕНИЕ ПАРАБОЛЫ - траектории точки P, равноудаленной от заданной точки, например F, и прямой, например y = -1.

x2 + (y - 1)2 = (y + 1)2 + (x - x)2, или после упрощения x2 = 4y. Это уравнение геометрического места точек, образующих параболу. Рассмотрим теперь точки пересечения произвольной невертикальной прямой y = mx + b с параболой x2 = 4y. Точки пересечения должны иметь координаты, удовлетворяющие одновременно обоим уравнениям, поэтому x2 = 4mx + 4b, или x2 - 4mx - 4b = 0. В общем случае существуют два решения x1 и x2 квадратного уравнения. Известно, что сумма этих решений x1 + x2 равна коэффициенту при x, взятому со знаком минус. Следовательно, x1 + x2 = 4m. Абсцисса средней точки M хорды P1P2 равна

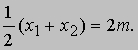
Результат зависит только от m и не зависит от b. Если теперь мы рассмотрим множество параллельных прямых с одним и тем же угловым коэффициентом m, но с различными значениями b, то середины всех хорд, высекаемых на этих прямых параболой, лежат на вертикальной прямой x = 2m (см. рис. 6).

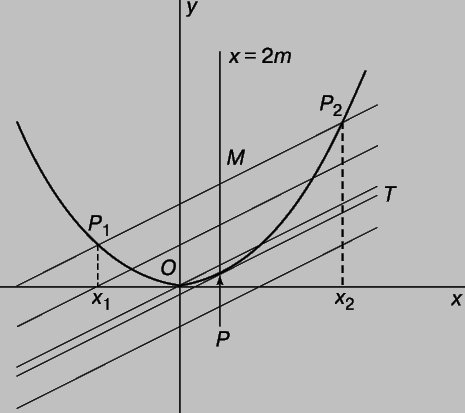
Рис. 6. ПАРАБОЛА, симметричная относительно оси y, пересечена семейством параллельных прямых с угловым коэффициентом m. Середины всех хорд, отсекаемых от этих прямых параболой, лежат на вертикальной прямой x = 2m. Касательная T к параболе пересекает ее в единственной точке P с координатами (2m,m2).

Среди этих параллельных прямых есть одна особенная прямая T, пересекающая параболу только в одной точке. Эта прямая называется касательной. Точка касания P имеет координаты (2m,m2).

Преобразование уравнений. Уравнение кривой зависит от положения координатных осей и от выбранных масштабов. Например, уравнение окружности с радиусом r единиц и с центром в начале координат имеет вид x2 + y2 = r2. Но если окружность расположена так, как показано на рис. 7, с центром в точке с координатами (h,k), то ее уравнение принимает более сложный вид:

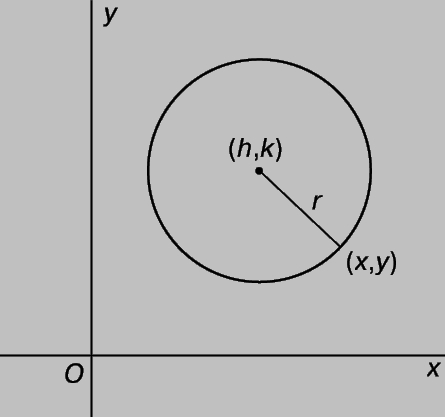
Рис. 7. ПРЕОБРАЗОВАНИЕ уравнений, связанное с различным расположением системы координат. Окружность с центром в точке (h,k) имеет иное уравнение, чем окружность с центром в начале координат O.

(x - h)2 + (y - k)2 = r2, в чем нетрудно убедиться, воспользовавшись формулой расстояния. Для исследования свойств кривой удобно расположить оси так, чтобы уравнение приняло по возможности более простой вид, как мы поступили в случае параболы. До сих пор мы исследовали кривую, заданную некоторым геометрическим условием, которому должны удовлетворять все принадлежащие ей точки, и вывели уравнение относительно заданной пары координатных осей. Обратная задача состоит в том, чтобы построить кривую, соответствующую данному уравнению, и исследовать геометрические свойства этой кривой или ее графика. Предположим, что мы хотим исследовать график кривой

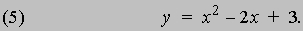
Перепишем это соотношение в виде y = x2 - 2x + 1 + 2 = (x - 1)2 + 2. Сделав затем замену переменных xў = x - 1 и yў = y - 2, сведем (5) к следующему уравнению:

которое, конечно, гораздо проще. Теперь заданную кривую можно записать в новой системе, оси которой параллельны старым с началом координат в точке x = 1, y = 2. Помимо такого приема (называемого параллельным переносом) - сдвига осей координат по горизонтали и по вертикали на соответствующие величины, уравнения часто упрощаются после поворота системы координат на некоторый угол вокруг неподвижного начала координат O. Оказывается, что этих двух приемов - параллельного переноса и поворота координатных осей, выполняемых по отдельности или вместе, - вполне достаточно, чтобы привести уравнение второй степени или к уравнениям двух прямых (пересекающихся, параллельных или совпадающих) или к одному из стандартных видов:

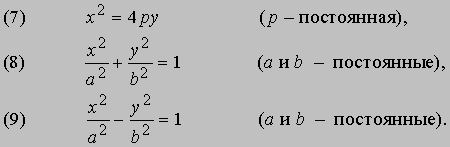
Уравнение (7) описывает параболу с фокусом в точке (0,p) и директрисой y = - p. Уравнение (8) соответствует эллипсу. Уравнение (9) описывает гиперболу (см. также КОНИЧЕСКИЕ СЕЧЕНИЯ). Помимо исследования графиков алгебраических уравнений, аналитическая геометрия изучает также неалгебраические, или трансцендентные, кривые, например графики экспоненциальных, логарифмических и тригонометрических функций. В качестве примера трансцендентной кривой приведем циклоиду - кривую, описываемую точкой окружности, катящейся без скольжения по прямой (рис. 8). Если в качестве прямой выбрать ось абсцисс, а радиус окружности принять равным 1, то координаты точки P будут иметь вид

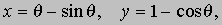
где q - угол в радианах.

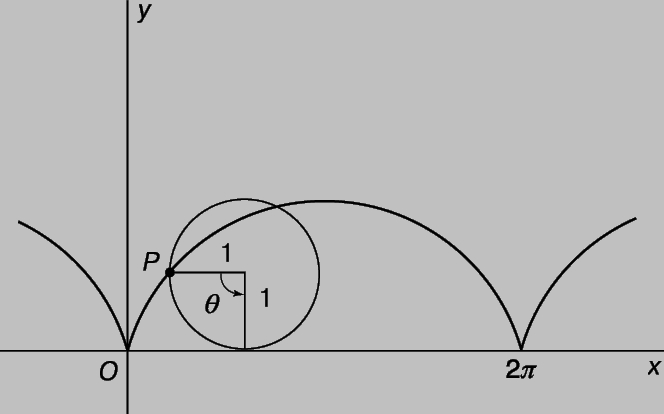
Рис. 8. ЦИКЛОИДА, кривая, определяемая как траектория точки окружности, катящейся по прямой без скольжения.

Циклоида обладает многими замечательными свойствами. Длина дуги циклоиды в 8 раз больше, чем длина катящейся окружности, а площадь под дугой в 3 раза больше площади катящегося круга. Если циклоиду перевернуть, то мы получим форму нити, по которой бусина соскальзывала бы до данной точки за кратчайшее время. Эти результаты доказываются методами математического анализа, а последний из них - методами вариационного исчисления. Циклоиды и аналогичные кривые, возникающие при движении одной окружности по другой, играют важную роль при проектировании зубчатых передач, действующих бесшумно и эффективно. На рис. 9 вы видите несколько других кривых и их уравнения.

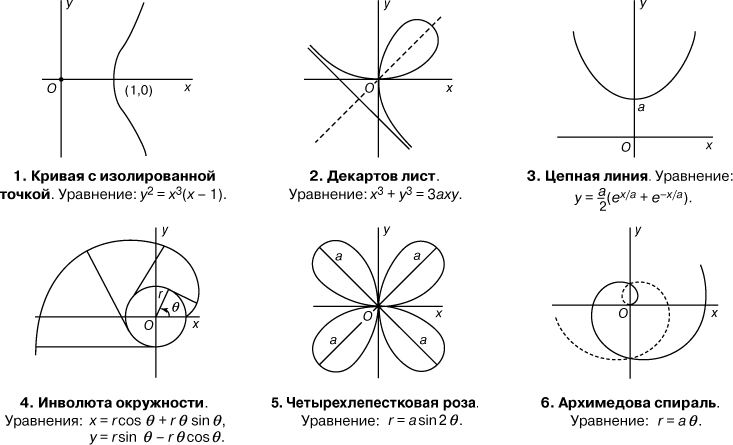
Рис. 9. РАЗЛИЧНЫЕ КРИВЫЕ и их уравнения.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

Методами аналитической геометрии исследуются также и пространственные фигуры. Нужно лишь воспользоваться тремя взаимно перпендикулярными осями, проходящими через начало координат О. Снабдив каждую ось шкалой, можно задать тремя числами (координатами) положение точки в пространстве. Например (рис. 10), P = (1,2,3).

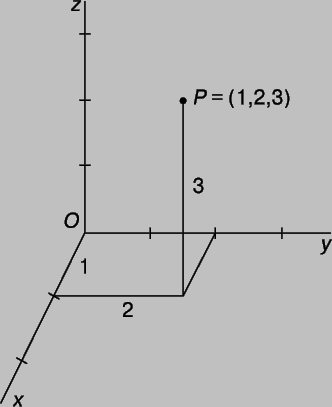
Рис. 10. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ требует трех взаимно перпендикулярных координатных осей и трех координат для задания положения точки. Точка P имеет координаты (1,2,3).

Множеству точек, удовлетворяющих некоторому геометрическому условию, соответствует определенное алгебраическое соотношение между их координатами x, y, z. Для задания этого соответствия необходима фундаментальная формула, определяющая расстояние d между точками P1 = (x1, y1, z1) и P2 = (x2, y2, z2), а именно: d2 = (x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2. Эта формула представляет собой обобщение теоремы Пифагора с двумерного случая на трехмерный. Из нее следует, что сфера радиуса r с центром в начале координат описывается уравнением x2 + y2 + z2 = r2. Любая плоскость задается уравнением первой степени относительно x, y и z, т.е. уравнением вида Ax + By + Cz = D, где A, B, C и D - постоянные и, по крайней мере, один из коэффициентов A, B или C не равен нулю. Помимо сферы есть и другие поверхности, также описываемые уравнением второй степени относительно x, y и z. Одна из задач аналитической геометрии в трехмерном пространстве состоит в том, чтобы дать классификацию таких квадратичных поверхностей и, исходя из соответствующих им уравнений, исследовать их свойства. Эти поверхности называются эллипсоидами, параболоидами, гиперболоидами или коническими и цилиндрическими поверхностями различных типов. Особенно простой подкласс этих фигур состоит из поверхностей, получаемых при вращении конических сечений вокруг различных осей симметрии. Существуют многочисленные поверхности, задаваемые уравнениями более высокого порядка. Как правило, они довольно сложны. Их изучением, как и плоских кривых высокого порядка, занимается алгебраическая геометрия. Как и в случае фигур на плоскости, исследование трехмерных геометрических тел часто облегчается подходящим выбором координатных осей. Соответствующее уравнение обычно удается упростить с помощью параллельного переноса и (или) поворота осей. Иногда бывает удобно воспользоваться непрямоугольной системой координат. Например, если в уравнение, записанное в прямоугольных координатах x, y и z, подставить x = r cos q, y = r sin q и z = z, то получится эквивалентное и нередко более простое уравнение в цилиндрических координатах r, q и z (рис. 11). Так, уравнение z = x2 + y2 сводится к уравнению z = r2.

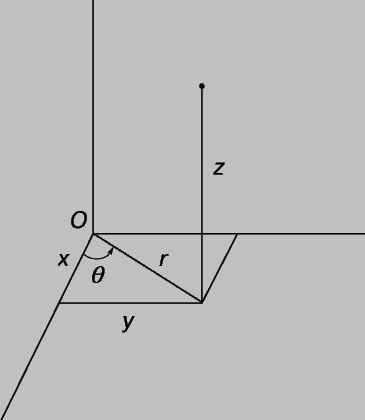
Рис. 11. ЦИЛИНДРИЧЕСКИЕ КООРДИНАТЫ иногда используются в геометрии трехмерного пространства для упрощения уравнений. Прямоугольные координаты x и y в этом примере заменены полярными r и q, а координата z оставлена без изменений.

Подстановка x = r cos q sin f, y = r sin q sin f, z = r cos f преобразует уравнение, заданное в прямоугольных координатах, в уравнение в сферических координатах r, q и f (рис. 12).

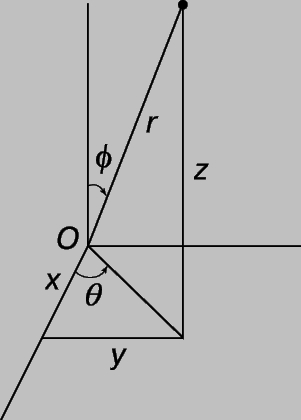
Рис. 12. СФЕРИЧЕСКИЕ КООРДИНАТЫ - трехмерный аналог полярных координат на плоскости. Положение точки однозначно определяется заданием расстояния r и двух углов - q, отсчитываемого от оси x, и f, отсчитываемого от оси z.

Аналитическая геометрия занимается также изучением прямых и кривых в трехмерном пространстве. Прямую можно рассматривать как линию пересечения подходящей пары плоскостей. Соответственно, пространственную прямую можно задать с помощью двух уравнений первого порядка. Однако часто бывает проще задать прямую L с помощью параметра t следующим образом: x = x0 + a1t, y = y0 + a2t, z = z0 + a3t. Когда t принимает все возможные действительные значения, мы получаем все возможные значения x, y и z для точек на L. При t = 0 мы получаем координаты x0, y0 и z0 некоторой точки P0; при t = 1 - координаты (x0 + a1, y0 + a2, z0 + a3) некоторой другой точки P1. Прямая L определяется двумя своими точками P0 и P1. Пространственную кривую можно также записать в виде x = f1(t), y = f2(t), z = f3(t), где f1, f2 и f3 - заданные функции. (Прямая соответствует случаю, когда все три функции имеют первую степень по t.) Например, x = cos t, y = sin t, z = t - уравнения винтовой линии, получающейся при наматывании нити на цилиндрическую поверхность радиуса 1 с постоянным шагом (рис. 13).

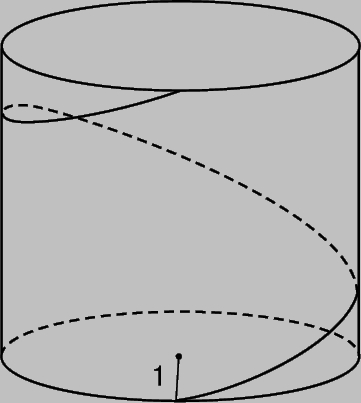
Рис. 13. ВИНТОВАЯ ЛИНИЯ, пространственная кривая, задаваемая радиусом и расстоянием между точками пересечения кривой с любой вертикальной прямой на поверхности цилиндра того же радиуса.

Более высокие размерности. Вполне естественно обобщить методы аналитической геометрии на случаи, когда число координат больше трех. Разумеется, невозможно представить себе наглядно гиперсферу x2 + y2 + z2 + w2 = r2 или гиперплоскость Ax + By + Cz + Dw = E. И все же мы можем воспользоваться теми же алгебраическими методами, как и в случаях двух или трех измерений, используя соответствующий им наглядный геометрический язык как подсказку, когда такая наглядность отсутствует. Более того, весьма плодотворным оказалось обобщение методов аналитической геометрии на бесконечномерные пространства. Многие важные разделы аналитической геометрии пространства трех и более измерений можно существенно упростить с помощью векторных методов (см. также ВЕКТОР).

ЛИТЕРАТУРА

Погорелов А.В. Аналитическая геометрия. М., 1978 Ильин В.А., Позняк Э.Г. Аналитическая геометрия. М., 1981

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ, раздел геометрии, в котором геометрические образы изучаются средствами алгебры. Существенным при этом является применение координат и исследование геометрических свойств по свойствам уравнений. Основы аналитической геометрии были заложены Р. Декартом (1637).

сущ., кол-во синонимов: 1

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ - 1) наука о кривых линиях 2-й степени. 2) приложение алгебры к геометрии.

Составить слова из слова аналитическая геометрия

Изложение правил механики при помощи одного математического анализа.

Составить слова из слова аналитическая механика

"АНАЛИТИЧЕСКАЯ ПСИХОЛОГИЯ" (комплексная психология) - направление глубинной психологии, основанной К. Г. Юнгом в 1913. Исходит из понимания психики как автономной саморегулирующей системы, основанной на взаимной компенсации сознания и бессознательного, интеграция которых - путь к достижению целостности личности, ее индивидуации. Оказала влияние на психопатологию и психотерапию, а также философскую антропологию, историю культуры, этнологию, мифологию и др. Международное общество аналитической психологии (с 1958) и ежегодник "Эранос" (с 1933 - в Цюрихе), "Журнал аналитической психологии" (с 1955 - в Лондоне).

Составить слова из слова аналитическая психология

Аналити́ческая филосо́фия - направление западной, главным образом англо-американской философии XX в.; сводит философию к анализу преимущественно языковых средств познания; разновидность неопозитивизма. Основные течения: 1) философия логического анализа, использующая аппарат современной математической логики, - логический эмпиризм (Р. Карнап, К. Гемпель, Ф. Франк) и логический прагматизм (У. Куайн, Н. Гудмен); 2) лингвистическая философия.

* * *

АНАЛИТИЧЕСКАЯ ФИЛОСОФИЯ - АНАЛИТИ́ЧЕСКАЯ ФИЛОСО́ФИЯ, направление западной, главным образом англо-американской, философии 20 в.; сводит философию к анализу преимущественно языковых средств познания; разновидность неопозитивизма (см. НЕОПОЗИТИВИЗМ). Основные течения:

1) философия логического анализа, использующая аппарат современной математической логики, - логический эмпиризм (Р. Карнап, К. Гемпель, Ф. Франк) и логический прагматизм (У. Куайн, Н. Гудмен);

2) лингвистическая философия (см. ЛИНГВИСТИЧЕСКАЯ ФИЛОСОФИЯ).

АНАЛИТИЧЕСКАЯ философия - направление западной, главным образом англо-американской, философии 20 в.; сводит философию к анализу преимущественно языковых средств познания; разновидность неопозитивизма. Основные течения: 1) философия логического анализа, использующая аппарат современной математической логики, - логический эмпиризм (Р. Карнап, К. Гемпель, Ф. Франк) и логический прагматизм (У. Куайн, Н. Гудмен);

2) лингвистическая философия.

АНАЛИТИЧЕСКАЯ ФИЛОСОФИЯ - преобладающее течение мысли в англоязычных странах 20 в.; способ философствования, ориентирующийся на идеалы ясности, точности и логической строгости. Последние были выражены, например, австрийским философом Людвигом Витгенштейном (1889-1951) в работе Tractatus Logico-Philosophicus (1921) следующим образом: "Цель философии - логическое прояснение мыслей". Примеры логического анализа можно найти в работах Платона и Аристотеля, средневековых теологов, рационалистов и эмпириков 17 и 18 вв., британских утилитаристов и в бесчисленном множестве сочинений других мыслителей. Вплоть до 20 в. философы обычно полагали, что главные философские вопросы - природа реальности, возможности и границы человеческого познания, природа добра и справедливости, смысл жизни - достаточно ясны, и задача философии заключается в том, чтобы дать на них ответы, причем неважно - ясные или не вполне понятные. Если идеал ясности должен быть отброшен ради того, чтобы найти истину, эту жертву следует принести не колеблясь. По мере развития философии возникали различные соперничавшие друг с другом "школы", каждая из них имела своих лидеров и последователей, свою методологию, свое мировоззрение (например, существовали школы томистов, картезианцев, кантианцев, немецких идеалистов, марксистов, прагматистов и др.). Некоторые из этих школ, отпраздновав краткий триумф, исчезали, другие продолжали жить, третьи со временем обретали новое дыхание. Однако сколько-нибудь заметного прогресса в поиске общезначимых решений главных философских проблем не наблюдалось. После двух тысячелетий развития философской мысли однозначные решения казались столь же недостижимыми, как и в древности. Возникновение аналитической философии означало надежду на прогресс. В конце 19 в. был разработан новый инструмент мышления - формальная логика. В том виде, который ей придали Г.Фреге, Б.Рассел и А.Н.Уайтхед, формальная логика позволила с большой точностью описать формы суждений и отношения между ними. На целый ряд философских вопросов, в частности касавшихся природы математики, были сразу даны новые и четкие ответы, и стало казаться, что с помощью формальной логики можно будет найти окончательное решение философских проблем. Б.Рассел назвал одну из своих лекций "Логика как сущность философии". Американский философ Ч.С.Пирс сформулировал суть нового подхода в своем знаменитом эссе Как сделать наши идеи ясными (1878). Хорошим примером использования логики в решении философских проблем является "теория дескрипций" Рассела в ее применении к проблемам истины и существования. Рассел задался вопросом: истинно или ложно утверждение "Нынешний король Франции лыс"? По-видимому, здесь мы имеем дело со следующей дилеммой. Утверждение явно не истинно, но, поскольку "нынешнего короля Франции" не существует, нельзя также сказать, что оно ложно, ибо тогда мы вынуждены будем сделать вывод о том, что нынешний король Франции не лыс. Анализ приведенного утверждения показывает, что оно представляет собой конъюнкцию трех более простых утверждений: "существует нынешний король Франции"; "существует не более чем один нынешний король Франции" и "если кто-то является нынешним королем Франции, то он лыс". Явно ложным является только первое из этих утверждений, и с ним уже не связано никаких проблем. Таким образом, анализируя логическую форму утверждения, мы можем прийти к более ясному пониманию его смысла и истинности, избегая неверных импликаций и псевдопроблем. Подобным же образом аналитический философ подходит к разрешению вечного вопроса: "В чем смысл жизни?" Сам вопрос кажется простым, хотя и не имеющим простого ответа. Но при более внимательном рассмотрении оказывается, что он тоже нуждается в прояснении. Понимаем ли мы, что такое "смысл" и что такое "жизнь"? Верно ли, что существует только один "смысл" и что вся "жизнь" имеет этот смысл? Допущения, которые мы принимаем, крайне сомнительны, следовательно, сомнительна и сама формулировка вопроса. Вопрос о смысле жизни должен быть задан как-то иначе, чтобы не были безнадежными все попытки его решения. Руководящий принцип аналитической философии в этом и других случаях, как его формулирует Витгенштейн в предисловии к Логико-философскому трактату, гласит: "То, что вообще может быть сказано, может быть сказано ясно; о том же, что сказать невозможно, следует молчать". В период примерно с 1920 по 1950 в рамках аналитической философии существовало мощное движение, известное под названием логического позитивизма. Возникло оно в Вене (отсюда наименование первого периода развития логического позитивизма - "Венский кружок"). Философы этого направления, М.Шлик, Р.Карнап, А.Дж.Айер и др., полагали, что все осмысленные утверждения являются либо научно верифицируемыми утверждениями о мире, либо чисто логическими тавтологиями. Суждения традиционной философии, как и многие суждения, принадлежащие сфере обыденной жизни, были объявлены бессмысленными. Для пропаганды своих идей "Венский кружок" созывал международные конференции, издавал собственный журнал и серию книг, поддерживал связи с близкими по взглядам философами в других странах. Концом логического позитивизма можно считать публикацию в 1950-х годах серии статей одного из бывших членов Венского кружка К.Гемпеля, в которых были отмечены принципиальные трудности и даже неясности, связанные с самим ключевым понятием осмысленности. Серьезная критика неопозитивистских принципов была проведена американским логиком У.В.О.Куайном. Руководствуясь идеалом ясности, аналитики занимались изучением не только логической структуры языка, но и его употребления в обыденных, повседневных контекстах. Подчеркивалось, что при анализе языковых выражений следует принимать во внимание эти контексты. Отрываясь от них, философы используют термины в специфических несобственных смыслах и поэтому сталкиваются с затруднениями, которые не могут быть устранены в принципе. Видными представителями этого течения (т.н. "анализа обыденного языка"), кроме "позднего Витгенштейна", были Г. Райл, Дж. Остин, Г. Э. М.Энском и Н. Малколм. Приблизительно с 1960 акценты сместились, и под влиянием Куайна язык и логика стали рассматриваться, подобно эмпирическим наукам, не просто как набор инструментов для анализа, а как некое знание о реальности. В результате в лоно философского анализа возвратились традиционные проблемы: истины, фактического соответствия, синтеза знания. Но поскольку требования ясности и логической строгости все еще считаются абсолютно необходимыми, термин "аналитическая философия" остается в своих правах, а обозначаемый им образ мышления продолжает господствовать в мире англоязычной философии.

См. также

КАРНАП Рудольф;

ВИТГЕНШТЕЙН Людвиг;

РАССЕЛ Бертран;

МУР Джордж Эдуард;

ФРЕГЕ Готлоб;

УАЙТХЕД Алфред Норт;

АЙЕР Алфред Джулс;

РАЙЛ Гилберт;

КУАЙН Уиллард ван Орман;

ОСТИН Джон;

ПИРС Чарлз Сандерс.

ЛИТЕРАТУРА

Геллнер Э. Слова и вещи. М., 1962 Хилл Т. Современные теории познания. М., 1965 Аналитическая философия. Избранные тексты. М., 1993

АНАЛИТИЧЕСКАЯ ФИЛОСОФИЯ, направление западной, главным образом англо-американской, философии 20 в.; сводит философию к анализу преимущественно языковых средств познания; разновидность неопозитивизма. Основные течения:

1) философия логического анализа, использующая аппарат современной математической логики, - логический эмпиризм (Р. Карнап, К. Гемпель, Ф. Франк - США) и логический прагматизм (У. Куайн, Н. Гудмен - США);

2) лингвистическая философия - философия обыденного языка (Г. Райл, Дж. Остин, Дж. Уисдом, П. Строусон - Великобритания).

Аналитическая философия

(analytic philosophy), направление в философии 20 в., получившее распространение в Австрии, Великобритании и США. А.ф. рассматривает осн. филос. проблемы с т. зр. выяснения или анализа таких понятий, как значение, истина, необходимость. Хотя А.ф. представляет собой свободную (как бы естественным образом сложившуюся) традицию, а не узкоспецифическую доктрину, в ней тем не менее существует общее согласие относительно ряда конкретных вещей. Философия считается особым ср-вом познания, к-рый использует методы, отличающиеся от методов естественных или обществ, наук; кроме того, в отличие, напр., от биологии или экономики, она не связана ни с какими конкретными фактами. Задача философии - не построение теорий, к-рые приумножают наше знание о мире, но прояснение самого знания и тех представлений, к-рыми мы уже обладаем. Это прояснение достигается при помощи анализа языка, к-рый применяется при формулировании филос. понятий. Общая схема оставляет, однако, простор для внутр. разногласий. В частности, существует разногласие между Расселом, с т.зр. к-рого подобный анализ дает ответы на традиц. вопросы метафизики и эпистемологии, и Витгенштейном, утверждающим, что подобные вопросы - рез-т недоразумения, к-рого можно избежать с помощью построения идеального (искусств.) языка. В связи с этим обсуждается вопрос, может ли филос. анализ проводиться в систематической форме на основе ср-в и методов мат. логики, как считают логические позитивисты (логический позитивизм), или решение филос. проблем требует детального анализа отд. сфер естественного, обыденного языка (лингвистическая философия). Представителей этого направления обвиняют в увлечении построением разных систем с якобы строгой аргументацией и ясностью выражения. Критики утверждают, что это течение бесплодно, ограничено частными моментами и игнорирует осн. филос. проблемы.

Составить слова из слова аналитическая философия

Составная словоформа. Например, в русском языке словоформы "буду писать", "буду говорить" - аналитические формы будущего времени глагола, "более хороший", "лучше всех" - аналитические формы разных степеней прилагательных.

Составить слова из слова аналитическая форма

В общем языкознании: грамматическая форма, у которой показатель грамматического значения находится за пределами слова.

Составить слова из слова аналитическая форма слова

Аналити́ческая фу́нкция - функция, которая может быть представлена в некоторой области степенным рядом. Большинство функций, встречающихся в математике и её приложениях, - аналитические функции. Теория аналитических функций - важнейшая часть теории функций комплексного переменного.

* * *

АНАЛИТИЧЕСКАЯ ФУНКЦИЯ - АНАЛИТИ́ЧЕСКАЯ ФУ́НКЦИЯ, функция, которая может быть представлена в некоторой области степенным рядом. Большинство функций, встречающихся в математике и ее приложениях, - аналитические функции. Теория аналитических функций - важнейшая часть теории функций комплексного переменного.

АНАЛИТИЧЕСКАЯ функция - функция, которая может быть представлена в некоторой области степенным рядом. Большинство функций, встречающихся в математике и ее приложениях, - аналитические функции. Теория аналитических функций - важнейшая часть теории функций комплексного переменного.

▲ функция (математическая)

аналитическая функция, голоморфная функция - функция, которая может быть представлена

степенным рядом.

Составить слова из слова аналитическая функция

Аналити́ческая хи́мия - рассматривает принципы и методы определения химического состава вещества. Включает качественный анализ и количественный анализ. Аналитическая химия возникла наряду с неорганической химией раньше других химических наук (до конца XVIII в. химия определялась как наука, изучающая химический состав веществ). Во 2-й половине XVII в. Р. Бойль ввёл понятие анализа состава тел, заложил основы аналитической химии как науки. Для аналитической химии характерно применение не только традиционных химических (гравиметрический анализ, титриметрический анализ), но и физико-химических (например, электрохимические методы анализа, фотометрический анализ) и физических (спектральный анализ, активационный анализ и др.) методов, а также биологических методов, основанных на изучении реакции микроорганизмов на изменения среды их обитания.

* * *

АНАЛИТИЧЕСКАЯ ХИМИЯ - АНАЛИТИ́ЧЕСКАЯ ХИ́МИЯ, рассматривает принципы и методы определения химического состава вещества. Включает качественный анализ (см. КАЧЕСТВЕННЫЙ АНАЛИЗ) и количественный анализ (см. КОЛИЧЕСТВЕННЫЙ АНАЛИЗ). Аналитическая химия возникла наряду с неорганической химией раньше других химических наук (до кон. 18 в. химия определялась как наука, изучающая химический состав веществ). Во 2-й пол. 17 в. Р. Бойль ввел понятие анализа состава тел, заложил основы аналитической химии как науки. Для аналитической химии характерно применение не только традиционных химических (гравиметрический анализ, титриметрический анализ), но и физико-химических (напр., электрохимические методы анализа, фотометрический анализ) и физических (спектральный анализ, акревационный анализ и др.) методов, а также биологических методов, основанных на изучении реакции микроорганизмов на изменения среды их обитания.

АНАЛИТИЧЕСКАЯ химия - рассматривает принципы и методы определения химического состава вещества. Включает качественный анализ и количественный анализ. Аналитическая химия возникла наряду с неорганической химией раньше других химических наук (до кон. 18 в. химия определялась как наука, изучающая химический состав веществ). Во 2-й пол. 17 в. Р. Бойль ввел понятие анализа состава тел, заложил основы аналитической химии как науки. Для аналитической химии характерно применение не только традиционных химических (гравиметрический анализ, титриметрический анализ), но и физико-химических (напр., электрохимические методы анализа, фотометрический анализ) и физических (спектральный анализ, акревационный анализ и др.) методов, а также биологических методов, основанных на изучении реакции микроорганизмов на изменения среды их обитания.

АНАЛИТИЧЕСКАЯ ХИМИЯ, изучает принципы и методы идентификации веществ и их компонентов (качественный анализ), а также определения количественного соотношения компонентов (атомы, молекулы, фазы и т.п.) в образце (количественный анализ). До 1-й половины 19 в. - основной раздел химии. Существенный вклад в развитие аналитической химии внесли Р. Бойль, Т. Бергман (Швеция), К. Фрезениус (Германия), Ж. Гей-Люссак, Ю. Либих, Ф. Прегль и др.

Составить слова из слова аналитическая химия