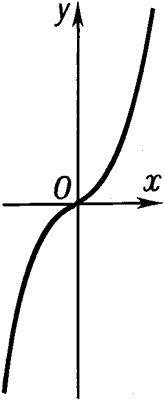
Куби́ческая пара́бола - алгебраическая кривая 3-го порядка: у = х³.

* * *

КУБИЧЕСКАЯ ПАРАБОЛА - КУБИ́ЧЕСКАЯ ПАРА́БОЛА, алгебраическая кривая 3-го порядка: y = x³ .

КУБИЧЕСКАЯ ПАРАБОЛА - алгебраическая кривая 3-го порядка: y = x3 .

Составить слова из слова кубическая парабола

Куби́ческая сингони́я - кристаллографическая сингония, для которой характерно соотношение между углами и рёбрами элементарной ячейки кристалла: а = b = с, α = β = γ = 90º. Подразделяется на 5 классов (точечных групп симметрии).

* * *

КУБИЧЕСКАЯ СИНГОНИЯ - КУБИ́ЧЕСКАЯ СИНГОНИ́Я, кристаллографическая сингония (см. СИНГОНИЯ), для которой характерно соотношение между углами и ребрами элементарной ячейки кристалла (см. ЭЛЕМЕНТАРНАЯ ЯЧЕЙКА КРИСТАЛЛА): a=b=c, a=b=g=90 °. Подразделяется на 5 классов (точечных групп симметрии (см. ТОЧЕЧНАЯ ГРУППА СИММЕТРИИ)). Это единственная сингония, симметрии которой отвечает обычная декартова система координат, элементарная ячейка - куб. У кристаллов кубической сингонии обязательно есть четыре оси 3 (третьего порядка), расположенные как пространственные диагонали куба.

КУБИЧЕСКАЯ сингония - кристаллографическая сингония, для которой характерно соотношение между углами и ребрами элементарной ячейки кристалла: a=b=c, ??????90 .. Подразделяется на 5 классов (точечных групп симметрии).

Составить слова из слова кубическая сингония