МЕХАНИКА - раздел физики, в котором изучается движение тел под действием сил. Механика охватывает очень широкий круг вопросов - в ней рассматриваются объекты от галактик и систем галактик до мельчайших, элементарных частиц вещества. В этих предельных случаях выводы механики представляют, конечно, чисто научный интерес. Но предметом механики является также проектирование строений, мостов и механизмов; этот раздел, обычно называемый прикладной механикой, сам по себе достаточно обширен. Фундаментальное значение для всей этой тематики имеет механика материальной точки, разделяющаяся на кинематику, предметом которой является математическое описание возможных движений материальной точки, и динамику, которая рассматривает движение материальных точек под действием заданных сил. Основные принципы динамики сведены в законы движения, которые в случае материальных точек имеют самый простой вид. Эти законы были впервые сформулированы в 1687 И.Ньютоном. Если материальные точки движутся с очень большими скоростями, то ньютоновские законы движения следует модифицировать в соответствии с теорией относительности; если же это частицы атомных масштабов, то необходима иная формулировка законов движения - так называемая квантовая механика. Ниже будет изложена ньютоновская механика; ее модификациям посвящены статьи ОТНОСИТЕЛЬНОСТЬ;
КВАНТОВАЯ МЕХАНИКА. Протяженное тело можно формально рассматривать как совокупность идеализированных материальных точек, совершенно не имея в виду атомное строение вещества. Выводы о движении таких тел можно делать, исходя из совокупности движений материальных точек. Здесь тоже проводится различие между кинематикой и динамикой и, кроме того, существует статика, изучающая условия равновесия твердых тел, на которые действуют внешние силы. Эти вопросы обсуждаются ниже. Механические свойства газов и жидкостей в какой-то мере сходны, и законы, которым подчиняется их движение, тоже можно вывести, рассматривая их как системы материальных точек. Этот раздел, обычно называемый "механикой жидкостей и газов", подразделяется на гидростатику и гидродинамику. Им посвящена статья ГИДРОАЭРОМЕХАНИКА. Специальные вопросы течения газов рассматриваются в статье АЭРОДИНАМИКА, а вопросы движения электропроводящих жидкостей и газов - в статье МАГНИТНАЯ ГИДРОДИНАМИКА. Остаются еще три специальных раздела - аналитическая динамика, небесная механика и статистическая механика. Аналитическая динамика - это математическая дисциплина, в центре внимания которой находятся общие методы составления уравнений движения и их решения, а не анализ конкретных механических систем. В небесной механике методы аналитической динамики применяются при изучении чрезвычайно сложного движения планетных систем. Статистическая механика опирается на теорию газов и рассматривает в общем виде поведение системы, содержащей огромное число молекул или атомов, исходя из свойств таких отдельных частиц и законов, управляющих их поведением. По этим вопросам имеются отдельные статьи
НЕБЕСНАЯ МЕХАНИКА;
СТАТИСТИЧЕСКАЯ МЕХАНИКА. Подобное деление механики отражает историческое развитие физики и, кроме того, соответствует использованию различных математических методов. В конечном итоге механика и физика как наука составляют единое целое, ибо чем больше мы узнаем, например, о таких явлениях, как свет и электричество, которые обычно не рассматриваются в механике, тем яснее становится их фундаментальная связь с атомными явлениями, тесно связанными с механикой. Исторически развитие статики началось с Архимеда в 3 в. до н.э. До этого периода и много столетий спустя проблемы динамики обсуждались лишь с качественной стороны и соотносились с принципами, которые мы полагаем сегодня ошибочными либо не имеющими отношения к делу. Начало динамике было положено Ньютоном, который сформулировал законы движения и закон всемирного тяготения, опубликованные в первом издании Математических начал натуральной философии (Philosophiae naturalis principia mathematica, 1687). Ньютону удалось в своей книге заложить основы, а в ряде случаев и далеко продвинуться в изучении динамики, небесной механики, механики твердого тела, гидродинамики и баллистики. Хотя принципы статики к тому времени были хорошо известны, Ньютон впервые рационально обосновал их, показав, как их можно вывести из законов динамики. На протяжении примерно двух столетий после этого механика развивалась путем построения более совершенных математических методов без необходимости внесения каких-либо изменений в основные принципы, и лишь после 1900 развитие теории электромагнетизма и атомной физики потребовало модификации механики для распространения ее принципов на явления, которые она не могла удовлетворительно описывать. Но теория относительности и квантовая механика не отменили ньютоновской теории - она по-прежнему точна, как и раньше, и можно показать, что она строго вытекает из обеих новых теорий в том случае, когда рассматриваемые тела имеют макроскопические размеры и движутся с умеренными скоростями. В остальной части этой статьи мы будем иметь дело только с такими ситуациями.
Механика материальной точки. Чтобы можно было описывать движение материальной точки, нужно определить ее положение в данный момент. На рис. 1 показана прямоугольная система координат, которая позволяет характеризовать положение материальной точки, находящейся в точке Р, координатами (x, y, z). Поскольку материальная точка не имеет размеров и, следовательно, не может быть ориентирована в том или ином направлении, эти три числа полностью характеризуют ее положение в любой момент. Если раcсматривать их как функции времени t, то функция [[x (t), y(t), z (t)]] прочерчивает в пространстве траекторию, полностью определяющую движение материальной точки. Основная задача динамики материальной точки - найти зависимость x, y и z от t, если заданы силы, действующие на материальную точку. (Возможна, конечно, задача о нескольких материальных точках, оказывающих силовое воздействие друг на друга; подобные задачи решаются труднее.)
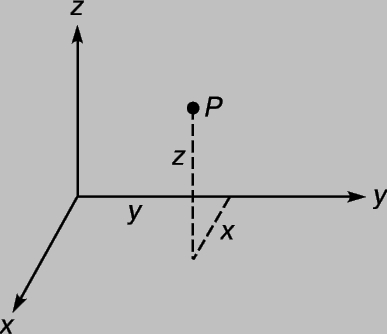
РИС. 1
Рассмотрим сначала материальную точку, движущуюся прямолинейно, скажем, вдоль оси x, в отсутствие каких-либо сил. В средневековой механике вслед за Аристотелем утверждалось, что тело движется, пока на него действует сила. Однако Галилей, а за ним и Ньютон установили, что единственное действие силы состоит в изменении движения тела и что в отсутствие силы тело либо остается в покое, либо продолжает двигаться равномерно и прямолинейно. В этом заключается первый закон механики Ньютона. Под равномерным движением подразумевается движение с постоянной скоростью v, при котором путь x, проходимый за время t, равен: x = vt. Точнее было бы формулировать это определение, рассматривая короткие интервалы пути и времени: если частица начинает двигаться из точки x0 в момент времени t0 и достигает точки х в момент t, то средняя скорость за это время определяется как
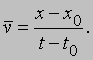
Конечно, если материальная точка движется с постоянной скоростью, то нет необходимости говорить о среднем значении. Но если на материальную точку действует сила, то ее движение не является равномерным. В этом случае скорость меняется во времени, и можно говорить о мгновенной скорости v (t) в момент времени t как пределе представленного выше выражения при очень малых интервалах времени и пути. Это записывается следующим образом:
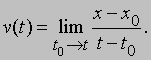
Точно так же можно говорить об изменении скорости во времени, т.е. об ускорении. Если мгновенная скорость изменяется от v0 в момент t0 до v в момент t, то среднее ускорение за этот промежуток определяется как
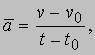
а мгновенное ускорение в момент времени t
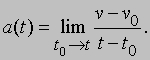
Таким образом, скорость характеризует быстроту изменения положения, а ускорение - быстроту изменения скорости. Рассматривать скорость изменения ускорения и т.д. не имеет особого смысла, поскольку, как это первым понял Ньютон, сила создает лишь ускорение. Действительно, если к небольшому телу приложена сила F, то, как показывает опыт, его ускорение остается постоянным, если сила постоянна, и в любой момент времени ускорение пропорционально этой силе. Данное положение можно записать в виде a МЕХАНИКА F или F МЕХАНИКА a. В этом соотношении коэффициент пропорциональности m есть величина, постоянная для рассматриваемой частицы независимо от того, где и как она движется. Эта величина m называется массой (инертной массой) частицы, и, следовательно, равенство F = ma
есть установленное опытным путем соотношение между мгновенными значениями величин F и a. В этом суть второго закона Ньютона. Третий закон, который мы приведем в дальнейшем, относится к случаю, когда имеется более одного тела. Единицы измерения механических величин вводятся следующим образом. На основе эталонов единиц длины и времени - метра и секунды - определяются единицы скорости - метр в секунду (м/с) и ускорения - метр в секунду в квадрате (м/с2). Единица массы килограмм (кг) определяется как масса международного прототипа килограмма, изготовленного из сплава иридия с платиной и хранящегося в Международном бюро мер и весов в Севре под Парижем. Единица силы в системе СИ называется ньютоном (Н) и определяется как сила, сообщающая телу массой 1 кг ускорение 1 м/с2. Таким образом, согласно второму закону Ньютона, 1 H = 1 кг*м/с2. Направление вектора ускорения совпадает с направлением вектора силы.
Тяготение. Представленное выше определение единицы силы, основанное на незыблемых физических принципах, тем не менее, не удобно для практических измерений. Удобнее исходить из понятия веса, т.е. силы притяжения Земли. Согласно закону всемирного тяготения, сформулированному тоже Ньютоном, между любыми двумя телами во Вселенной действует сила притяжения, пропорциональная произведению масс этих тел и обратно пропорциональная квадрату расстояния между ними. Это положение математически выражается соотношением
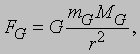
где G - универсальная гравитационная постоянная, а mG и MG - гравитационные массы тел. Если тела протяженные, то все материальные точки этих тел попарно взаимодействуют друг с другом в соответствии с этой формулой и, чтобы найти полную силу, нужно суммировать все отдельные взаимодействия. В чрезвычайно важном случае тел сферической формы оказывается, что притяжение будет в точности таким, как если бы масса каждого из них находилась в центре сферы. Предположим теперь, что телу с гравитационной массой mG и инертной массой m, удерживаемому не очень высоко над поверхностью Земли, предоставляется возможность свободно падать. Сила тяжести ускоряет тело вниз, и мы имеем
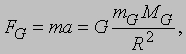
где MG - гравитационная масса Земли, а R - ее радиус. Ускорение падающего тела можно записать в виде
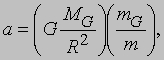
где первый множитель не зависит от свойств тела. Экспериментально установлено, что ускорение несколько изменяется в разных точках на поверхности Земли, поскольку Земля не является идеальной сферой и к тому же вращается. Однако в данном месте оно в точности одно и то же для всех тел. Это означает, что величины m и mG всегда и всюду пропорциональны, а при надлежащем выборе единиц измерения одинаковы. В таком случае нет необходимости различать гравитационную и инертную массы, и выражение для FG приобретает вид
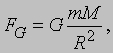
где
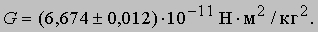
Аналогично выражению для ускорения a, ускорение силы тяжести g в любой точке дается формулой
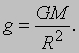
Величина g составляет примерно 9,81 м/с2 и позволяет определить массу Земли (5,97*10 24 кг) и ее среднюю плотность, в 5,5 раз превышающую плотность воды. Предположим, теперь, что вес тела равен W. Так как сила веса создает ускорение g, соотношение между массой, весом и ускорением приобретает вид W = mg.
Между экватором и полюсами на поверхности земли величина g изменяется от 9,78 до 9,83 м/с2. Соответственно этому изменяется и вес, но в одной точке вес двух тел с одинаковой массой всегда одинаков, и на этом опытном факте основан гораздо более удобный способ измерения массы и силы, нежели основанный на втором законе Ньютона. Массы двух тел равны, если в одном и том же месте равны их веса.
Импульс и энергия. Импульс тела р определяется как произведение его массы на скорость: p = mv.
Эта величина имеет важное значение. В самом деле, предположим, что два тела с массами m и M действуют друг на друга с силой, стремящейся ускорить оба тела. На рис. 2 такую силу создает пружина (происхождение силы может быть любым). Согласно третьему закону Ньютона, в любой момент времени сила, с которой масса m действует на массу M, равна по величине и противоположна по направлению силе, с которой масса M действует на m (действие равно противодействию). Предположим, что в момент времени t0 скорости масс равны v0 и V0. Комбинируя выражение для ускорений со вторым законом Ньютона, мы найдем, что скорости изменяются в соответствии с выражениями
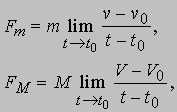
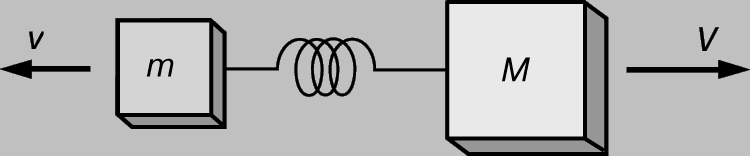
РИС. 2
где Fm и FM - силы, действующие на m и M. Поскольку эти силы равны и противоположно направлены, имеем
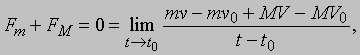
откуда, умножая на (t - t0) получаем
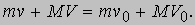
Из этого равенства следует, что хотя отдельные импульсы изменяются, их сумма в момент времени t0 равна их же сумме в момент t, т.е. в процессе всего движения остается постоянной. Это - так называемый закон сохранения импульса. Он универсален в том смысле, что справедлив независимо от природы сил и длительности их действия между телами. Работа U, совершаемая силой, приложенной к движущемуся телу, определяется как произведение силы на расстояние: U = F(x - x0),
где (как и далее) точки x и x0 должны выбираться достаточно близко друг к другу, чтобы силу F можно было считать постоянной. Воспользуемся тем, что, как легко доказать, точка, движущаяся с постоянным ускорением, проходит за время (t - t0) такое же расстояние, как если бы все это время она двигалась со средней скоростью 1/2(v + v0). Таким образом, из выражения для второго закона Ньютона вытекает:
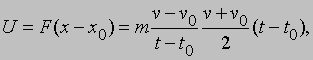
или
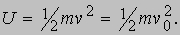
Величина 1/2mv2 называется кинетической энергией. Если обозначить ее через Т, то выражение U = T - T0
означает, что работа, совершаемая за любой малый промежуток времени, а следовательно (если просуммировать), и за любой произвольный промежуток времени, равна разности конечной и начальной кинетических энергий. Это положение справедливо независимо от того, какова сила и как она изменяется со временем, а также от того, каково расстояние, на котором она действует. Путем точно таких же рассуждений можно показать, что тело, обладающее кинетической энергией Т, может совершить работу, равную T - T0, если его Т уменьшится до величины T0, или равную Т, если тело в конце останавливается. Таким образом, всю работу, совершенную над телом при его ускорении, можно снова получить, остановив тело. Поэтому движущееся тело можно рассматривать как "носителя" работы. Под энергией понимается способность совершать работу, а запасенная телом кинетическая энергия зависит только от его скорости (и массы) и не зависит от того, как эта скорость была приобретена. Предположим, что тело массой m поднято на высоту h над поверхностью земли, а затем свободно падает. Если оно падает в течение времени t с постоянным ускорением g, то соотношение между g, h и t можно получить из правила для средних скоростей
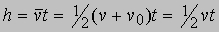
где v - скорость, с которой тело ударяется о землю, причем мы положили v0 = 0, поскольку до начала падения тело покоится. Вновь, поскольку v = gt, можно написать h = v2/2g, а умножив обе части равенства на mg, получим mgh = 1/2mv2.
Поскольку mg - вес тела, величина mgh есть работа по подъему тела на высоту h, а 1/2mv2 - кинетическая энергия тела в момент достижения им земли, равная работе, которую тело может совершить при ударе. Анализируя весь процесс, мы видим, что работа по подъему тела, равная mgh, запасается телом в виде его потенциальной энергии перед тем, как оно начинает падать. По мере падения потенциальная энергия переходит в кинетическую, которая может снова перейти в работу, равную mgh, при ударе тела о землю. Когда тело окончательно приходит в состояние покоя, то на первый взгляд энергия исчезает. Но более тщательный анализ показывает, что она сохранилась в форме усилившегося молекулярного движения в месте падения, т.е. в форме звука и теплоты. В отличие от импульса, энергия принимает разные формы, но при переходе из одной формы в другую полное количество энергии не меняется. Это - так называемый закон сохранения энергии. В качестве примера применения двух законов сохранения рассмотрим соударение двух шаровых маятников (рис. 3,а). Предположим, что шары маятников имеют одинаковую массу и изготовлены из абсолютно упругого материала. Это означает, что кинетическая энергия при ударе не рассеивается. Пусть V1 - скорость первого маятника в момент, предшествующий соударению, и нам надо найти v1 и v2 - скорости сразу после удара.
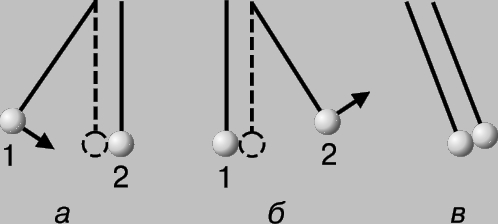
РИС. 3
При соударении энергия и импульс сохраняются, и мы имеем
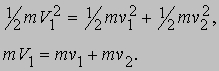
Производя сокращения и возводя обе части второго равенства в квадрат, получаем
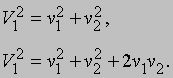
Эти соотношения могут выполняться одновременно только при v1v2 = 0. Таким образом, либо v1 = 0, либо v2 = 0, но не то и другое. Поскольку второй шар служит препятствием для первого, в нуль обратится v1, и в силу закона сохранения импульса системы имеем v2 = V1. Первый шар останавливается, а второй движется со скоростью V1, как показано на рис. 3,б. Предположим теперь, что на второй шар нанесена мастика, так что при соударении шары прилипают друг к другу и дальше движутся вместе (рис. 3,в). В этом случае v2 = v1 и импульс по-прежнему сохраняется, так что mV1 = 2mv1,
откуда v1 = 1/2V1, т.е. шары будут двигаться со скоростью, которая в два раза меньше начальной скорости первого шара. Начальное значение кинетической энергии равнялось T1 = 1/2mV12, а конечное значение 2*1/2m(1/2V1)2 = 1/2T1. Таким образом, кинетическая энергия, равная 1/2T1, рассеивается, причем основная часть этой потери идет на деформацию и нагрев мастики и шаров. Динамика и статика в трех измерениях. Чтобы обобщить предыдущие результаты на случай трех измерений, потребуется ввести лишь еще один принцип, который заключается в том, что законы Ньютона справедливы для движения вдоль каждой оси координат независимо от движения по другим осям. Так, если пренебречь сопротивлением воздуха, снаряд вдоль оси z движется с замедлением (рис. 4), а вдоль горизонтальной оси - без внешних сил и без ускорения. Обозначим через t время полета. Половину этого времени снаряд поднимается, а остальное время опускается. Таким образом, его скорость по вертикали изменяется на v0z за время 1/2t, так что
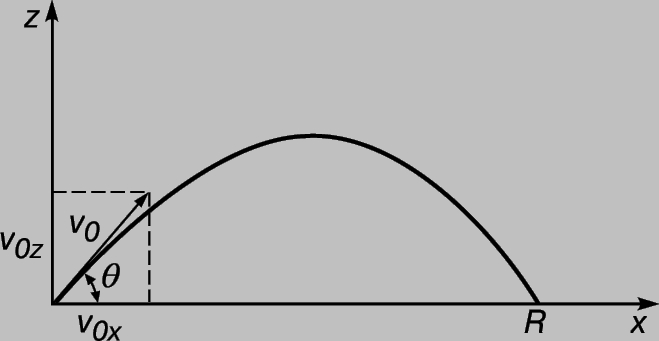
РИС. 4
v0z = 1/2gt, t = 2v0z/g, и все это время горизонтальное движение происходит со скоростью v0x и без ускорения. Таким образом, дальность полета равна: R = v0xt = 2v0xv0z/g. Если v0 - начальная скорость, а q - угол возвышения, то легко понять, что v0x = v0cosq и v0x = v0sinq , так что
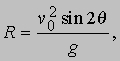
и максимальное значение этой величины, равное v02/g, достигается при q = 45°. В приведенном примере начальная скорость v0 характеризовалась и величиной, и направлением. Такие величины называются векторами, а величины v0x и v0z - соcтавляющими или компонентами вектора. (Обычно векторы обозначают полужирными буквами.) Предположим теперь, что в трехмерном пространстве к покоящейся материальной точке приложено несколько сил, под действием которых она остается в покое. О подобной системе сил говорят, что они уравновешены, и законы динамики позволяют определить, каким должно быть соотношение между ними. Если материальная точка покоится и сохраняет это состояние, ее ускорения вдоль осей x, y или z равны нулю, а поскольку ускорения вдоль этих осей не зависят друг от друга, полные силы в каждом из этих трех направлений тоже должны быть равны нулю. (Полная сила, действующая на материальную точку вдоль оси х и стремящаяся привести ее в движение вдоль этой оси, равна сумме x-компонент всех действующих сил; то же самое справедливо и для двух других осей.) Предположим, что имеются только две силы с компонентами F1x, F1y, F2x и F2y (для упрощения рисунка ограничимся двумя измерениями). В случае равновесия имеем F1x + F2x = 0 и F1y + F2y = 0, или F1x = -F2x и F1y = -F2y . Так как F1x и F1y - компоненты вектора силы F1, и аналогично F2x и F2y - компоненты вектора F2, то возникает ситуация, показанная на рис. 5, где векторы двух уравновешивающих друг друга сил изображены равными по величине и направленными в противоположные стороны.
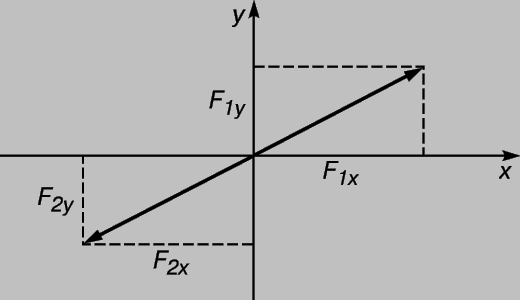
РИС. 5
Предположим, теперь, что имеются три вектора, причем F3 уравновешивает F1 и F2. В этом случае F1x + F2x + F3x = 0, F1y + F2y + F3y = 0. Эти соотношения можно переписать в виде F1x + F2x = -F3x, F1y + F2y = -F3y. Сравнение с аналогичными соотношениями в случае двух сил показывает, что если мы введем новый вектор R с компонентами Rx = F1x + F2x, Ry = F1y + F2y, который называется равнодействующей сил F1 и F2, то R будет в точности уравновешивать F3. Таким образом, сила R воспроизводит суммарное действие сил F1 и F2 в том смысле, что если удалить силы F1 и F2, заменив их силой R, то материальная точка по-прежнему останется бы в равновесии. Все сказанное представлено графически на рис. 6,а, где показано сложение компонент. На рис. 6,б вспомогательные линии убраны и оставлены только векторы. Последний рисунок называется параллелограммом сил. Он иллюстрирует один из фундаментальных принципов статики, который, как мы видели, является следствием динамической теории. Этот принцип был установлен С.Стевином (1548-1620), который показал, что если бы это было не так, то имелась бы возможность создать машину, которая производила бы работу, даже если бы к ней не подводилась энергия. Сегодня мы рассматривали бы такую машину как пример нарушения закона сохранения энергии; для Стевина это просто противоречило здравому смыслу, но при этом положения статики тоже обосновывались динамическими соображениями.
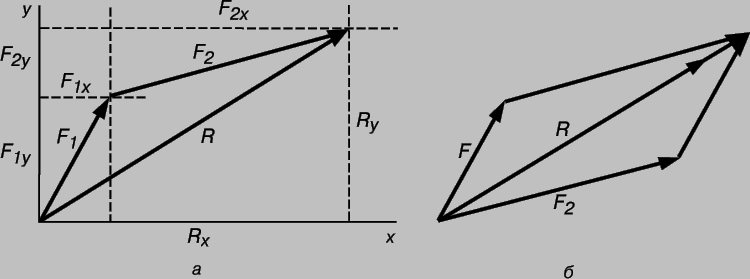
РИС. 6
Механика твердого тела. Твердое тело, которое может принимать различные ориентации в пространстве, можно считать состоящим из материальных точек. (Это просто математический прием, позволяющий расширить применимость законов движения материальных точек, но не имеющий ничего общего с гипотезой атомного строения вещества.) Поскольку материальные точки такого тела будут двигаться в разных направлениях с разными скоростями, приходится прибегать к процедуре суммирования. Рассмотрим систему, изображенную на рис. 7. Сила F, приложенная к тросу, заставляет массу, имеющую форму цилиндра, изменять свою скорость вращения. Будем характеризовать ориентацию цилиндра углом q между радиусом, проведенным из центра цилиндра в некоторую точку на нем, и произвольно выбранным направлением отсчета. Угол q измеряется в радианах; один радиан (примерно 57°) есть центральный угол, стягивающий дугу длиной r на окружности радиуса r. Таким образом, произвольный угол q стягивает дугу s, равную rq, а вся окружность сoответствует углу 2p радиан. Скорость любой точки на окружности равна
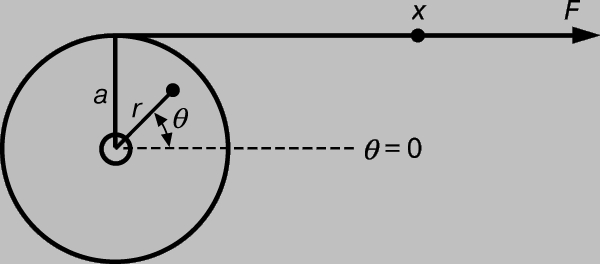
РИС. 7
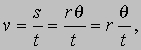
где под q /t понимается скорость, с которой изменяется угол q при вращении. Обозначив эту угловую скорость через w, мы наряду с равенством s = rq
получим v = rw. Нетрудно вычислить кинетическую энергию цилиндра, вращающегося вокруг неподвижной оси с угловой скоростью w. Обозначим через m одну из материальных точек цилиндра, расположенную на расстоянии rm от оси. Ее кинетическая энергия равна 1/2m(rmw)2, а полная кинетическая энергия всех материальных точек может быть представлена в виде суммы
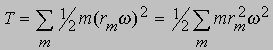
или T = 1/2Iw2, где
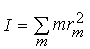
. Величина I, называемая моментом инерции, зависит от распределения массы в цилиндре и является его характеристикой. Момент инерции можно вычислить путем интегрирования, и для однородного цилиндра он равен 1/2Ma2, где M - масса цилиндра, а a - его радиус. Если цилиндр вращается свободно и нет сил, которые совершали бы над ним работу, то из закона сохранения энергии следует, что его кинетическая энергия остается постоянной. В таком случае постоянна и величина w, и мы имеем вращательный аналог первого закона Ньютона. Предположим теперь, что к тросу, намотанному на цилиндр, на короткое время от t0 до t прилагается сила F и за это время точка, отмеченная на тросе, проходит расстояние от x0 до х, а цилиндр поворачивается на угол от q0 до q, причем x - x0 = a(q -q0).
Работа, совершенная при этом силой, равна:
U = F(x - x0) = Fa(q - q0),
и точно так же, как при выводе выражения U = 1/2mv2 - 1/2mv02, мы можем выразить угловое перемещение через среднюю угловую скорость на этом интервале:
q - q0 = 1/2(w +w0)(t - t0),
так что U = 1/2Fa(w +w0)(t - t0).
За счет этой работы кинетическая энергия цилиндра изменяется от T0 до T, так что U = 1/2 I(w2 - w02).
Приравнивая два последних выражения и производя упрощения, получаем выражение
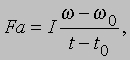
напоминающее формулу для ускорения частицы. Поэтому мы можем ввести угловое ускорение
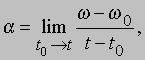
и тогда для малого интервала от t0 до t получим L = Ia, т.е. вращательный аналог второго закона Ньютона, в котором величина Fa, вызывающая вращение, обозначена через L. Она называется вращающим моментом. Изложенное можно обобщить на случай, когда отсутствуют неподвижные оси и тело свободно вращается в пространстве. В этом случае имеются три момента инерции, относящиеся к "главным осям". Мы не будем углубляться в рассмотрение этих вопросов. Однако можно вывести второй основной принцип статики для случая твердых тел. Пусть силы F1 и F2, приложенные к пластине, которая может вращаться, таковы, что вращения нет (рис. 8). Равновесие означает отсутствие углового ускорения, и поэтому полный вращающий момент равен нулю. Моменты сил F1 и F2 компенсируют друг друга при условии:
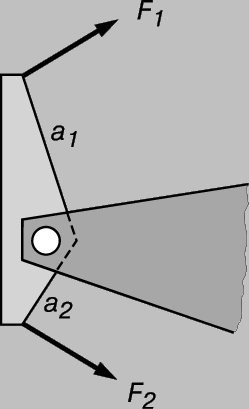
РИС. 8
F1a1 = F2a2,
т.е. получается закон рычага, известный со времен Архимеда. Удалим ось и заменим ее действие третьей силой, как показано на рис. 9, предполагая, что весом пластины можно пренебречь. Для равновесия всех этих сил нужно, во-первых, чтобы пластина не перемещалась и, следовательно, компоненты сил удовлетворяли условию векторного равновесия и, во-вторых, чтобы не было вращения, т.е. выполнялось выведенное только что соотношение. Оба эти принципа составляют основу теории строительной механики и важны при проектировании мостов и зданий.
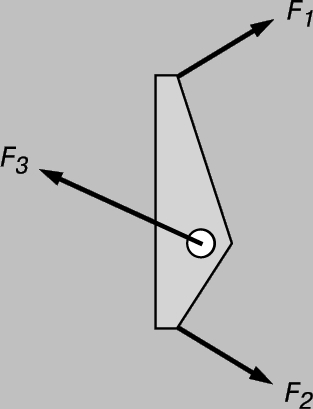
РИС. 9
Проводившиеся выше рассуждения упрощаются, если пользоваться обозначениями математического анализа, в которых подразумевается предельный переход (t (r) t0), так что нет необходимости все время говорить о нем. Ньютон первым применил методы дифференциального и интегрального исчисления при решении физических задач, а последующее развитие механики как науки было делом таких математиков, как Л. Эйлер, Ж. Лагранж, П. Лаплас и К. Якоби, каждый из которых находил в ньютоновской механике источник вдохновения для своих математических изысканий.
ЛИТЕРАТУРА
Фейнман Р., Лейтон Р. Фейнмановские лекции по физике, т. 1. Современная наука о природе. Законы механики. М., 1965 Бухгольц Н.Н. Основной курс теоретической механики. М., 1972 Веселовский И.Н. Очерки по истории теоретической механики. М., 1974 Григорьев В.И., Мякишев Г.Я. Силы в природе. М., 1988