Скорость любой химической реакции зависит от условий, в которых она протекает: от концентрации реагентов (или их давления, если это газы), температуры, наличия катализатора или излучения и т.д. Одни реакции протекают практически мгновенно (например, нейтрализация кислоты основанием), другие при обычных условиях идут настолько медленно, что заметные изменения концентраций реагентов наблюдаются лишь через несколько лет (например, взаимодействие водорода с кислородом с образованием воды в отсутствие катализатора). При этом существует множество реакций, протекающих с вполне измеримыми скоростями в обычных условиях. Химическая кинетика занимается определением скоростей химических реакций и изучением их механизма. Это относительно молодая наука, и в ней имеется много нерешенных проблем. Во всех кинетических исследованиях фигурируют время и промежуточные продукты (вещества, образующиеся на промежуточных стадиях реакции). Этим они отличаются от исследований систем в условиях химического равновесия, когда рассматриваются только начальное и конечное состояния реагентов.
См. также ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА.
ХИМИЧЕСКАЯ КИНЕТИКА
В одном кинетическом эксперименте нередко участвуют одновременно две или несколько реакций, при этом их скорости могут зависеть от наличия загрязнений и следов катализаторов. В результате получаемые данные бывают плохо воспроизводимыми, что затрудняет их интерпретацию. Если с термодинамической точки зрения из одних и тех же исходных веществ возможно образование разных продуктов, следует подбором концентрации реагентов, температуры и специфического катализатора добиться, чтобы протекала именно та реакция, которая интересует исследователя. Скорость реакций обычно определяют при постоянной температуре, лучше при двух и более ее значениях, используя один или несколько высокоточных термостатов.
Измерение скоростей реакций. Скорости реакций измеряют разными способами. Можно отбирать пробы из термостатируемого реактора через строго определенные интервалы времени либо замедлять или полностью останавливать реакцию (быстрым охлаждением реактора или каким-либо иным способом) и анализировать пробы титрованием или другими аналитическими методами. Иногда одновременно запускают несколько идентичных реакций, а затем последовательно останавливают их быстрым охлаждением и анализируют продукты. Если один из реагентов или продуктов реакции обладает оптической активностью, то следят за его концентрацией с помощью поляриметра. Аналогично, если изменение концентрации реагента или продукта реакции либо их обоих сопровождается изменением электропроводности, для кинетических измерений используют электрические методы. Иногда концентрацию одного из реагирующих веществ определяют, измеряя оптическую плотность раствора при определенной длине волны и используя закон Ламберта - Бера.
См. также ХИМИЯ АНАЛИТИЧЕСКАЯ. Скорость реакции можно рассчитать исходя из данных об изменении давления или объема в газофазной системе либо объема газа, выделяющегося в ходе реакции. В случае газофазных реакций, протекающих в потоке, в реактор иногда вводят катализатор или повышают температуру, чтобы ускорить процесс. Входные и выходные трубки в таких системах делают достаточно малыми, чтобы газы поступали в реактор и выходили из него как можно быстрее и в области с неконтролируемым градиентом температуры находились непродолжительное время. Время нахождения газов в реакторе (время протекания реакции) определяют исходя из объема газов, проходящих через реактор в 1 с, отнесенного к объему реактора. Если общее число молекул в ходе реакции изменяется, то оценить время становится довольно трудно. В проточных системах используются большие количества реагентов и получаются большие количества продуктов, что облегчает моделирование соответствующих химических процессов в промышленных масштабах. Скорость реакции можно определить по уменьшению концентрации исходных веществ или по увеличению концентрации продуктов. Скорость уменьшения концентрации исходного вещества равна -dC/dt, а скорость увеличения концентрации продукта равна dC/dt, где С - концентрация, t - время. Концентрацию обычно измеряют в единицах молярности (моль/л), время - в секундах.
Порядок реакции. Порядок реакции - это эмпирическая величина, равная сумме показателей степеней, с которыми концентрации реагентов входят в выражение для скорости реакции. Так, для реакции aA + bB -> mM + nN скорость уменьшения концентрации С реагента А можно представить в виде
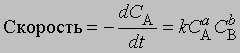
где СА и СВ - концентрации исходных веществ А и В соответственно. Порядок реакции в этом случае равен а + b. Коэффициент пропорциональности k, входящий в уравнение, называется константой скорости. Он равен скорости реакции при единичной концентрации реагентов.
Реакции первого порядка. Если скорость реакции зависит от концентрации только одного реагента в первой степени, то выражение для скорости принимает вид

О такой реакции говорят, что она является реакцией первого порядка. Чтобы найти зависимость концентрации от времени, нужно проинтегрировать уравнение (1). Разделив переменные и проинтегрировав, получим -ln C = kt + const
где ln - натуральный логарифм. Или, перейдя к десятичным логарифмам:
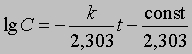
График зависимости lg C от t является прямой с тангенсом угла наклона -s, равным -k/2,303. Отсюда k = 2,303*s
Зная k и концентрацию С при данном t, можно найти константу интегрирования (const) и рассчитать концентрацию для любого момента времени. Константу интегрирования можно также определить из координат точки пересечения прямой с осью lg C при t = 0 (рис. 1).
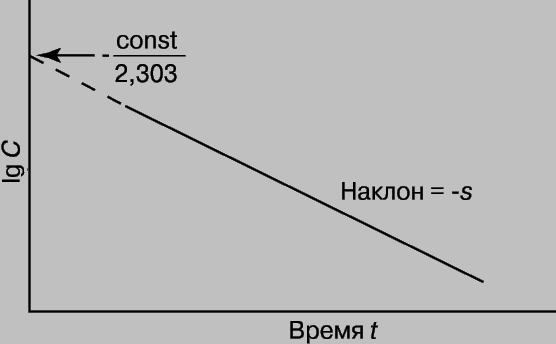
Рис. 1. ГРАФИК ЗАВИСИМОСТИ логарифма концентрации от времени.
Уравнение (1) можно проинтегрировать в пределах от С1 до С2, равных концентрациям реагента в моменты времени t1 и t2:

Отсюда
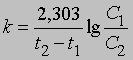
Размерность k равна размерности t -1. Если в начальный момент времени (t1 = 0) C1 = C0, то концентрация C в любой момент времени t в соответствии с уравнением (2) будет равна
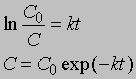
Уравнение (1) можно записать в другом виде, приняв, что а - это начальное количество реагента, x - его количество, прореагировавшее за время t. Тогда (а - x) равно количеству реагента, оставшемуся через время t, и уравнение реакции примет вид
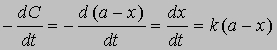
Разделив переменные и проинтегрировав, получим -ln(a - x) = kt + const
отсюда при t = 0, x = 0 и const = -ln a
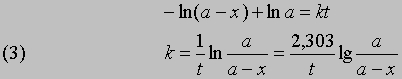
Часто представляет интерес характеристическая величина t1/2 - время полупревращения реакции, т.е. время, за которое концентрация исходного вещества уменьшается вдвое. При x = (1/2)a и t = t1/2 из уравнения (3) получим
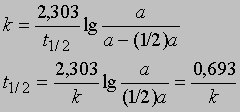
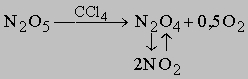
Это соотношение иллюстрирует важную особенность реакций первого порядка: время, за которое количество вещества уменьшается вдвое, не зависит от его количества в момент начала реакции и в любой данный момент реакции. Если известна константа скорости k, можно рассчитать количество вещества, прореагировавшего к данному моменту времени, или определить, за какое время прореагирует данное количество вещества. Уравнению первого порядка следуют многие химические реакции. Например, пентаоксид азота, растворенный в тетрахлориде углерода, разлагается при температуре 45° С в строгом соответствии с уравнением реакции первого порядка:
Реакции второго порядка. Когда скорость реакции пропорциональна квадрату концентрации отдельного реагента или концентрациям каждого из двух реагирующих веществ в первой степени, мы имеем дело с реакцией второго порядка. В дифференциальной форме выражения для скорости такой реакции имеют вид
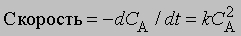
и
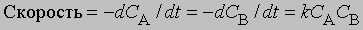
Пусть a - начальная молярная концентрация реагента А, x - число его молей в 1 л, прореагировавшее за время t; тогда скорость реакции будет равна dx/dt = k(a - x)2
или dx/(a - x)2 = kdt
Проинтегрировав, получим 1/(a - x) = kt + C
Поскольку x = 0 при t = 0, константа С = 1/а. Отсюда
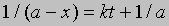
и
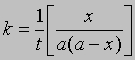
Если а и b - начальные молярные концентрации реагентов А и В соответственно и если за время t прореагировало x молей этих реагентов в 1 л, то, проинтегрировав соответствующее уравнение для скорости реакции, можно найти выражение для константы скорости:
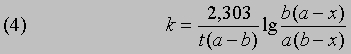
Размерность k - л/(моль*с). Численное значение k можно найти, подставив концентрации и время в уравнение (4) либо построив графики зависимости
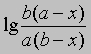
или
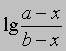
от времени. Умножение наклона полученной таким образом прямой на 2,303/(a - b) дает k.
Реакции третьего порядка. Скорость реакции третьего порядка может зависеть от концентрации одного реагента в третьей степени, либо концентрации одного реагента во второй степени и второго реагента в первой степени, либо от концентрации каждого из трех реагентов в первой степени. Так,
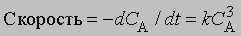
или dx/dt = k(a - x)3
Разделение переменных и интегрирование дают
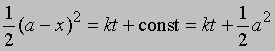
или
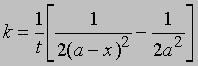
Здесь размерность k - л2/(моль2*с). Реакции нулевого порядка. Скорость реакций нулевого порядка не зависит от концентраций реагентов и определяется другими лимитирующими факторами, например площадью поверхности катализатора (в реакциях гетерогенного катализа) или поглощением света (в фотохимических реакциях). Уравнение для скорости такой реакции в дифференциальной форме имеет вид -dC/dt = k
или, выраженное через концентрацию x продукта, dx/dt = k
Проинтегрировав, получим x = kt + C
Значению x = 0 соответствует t = 0, откуда константа С = 0 и x = kt
В величину k могут входить различные константы, например интенсивность света, концентрация насыщенного раствора или пара. Размерность k - моль/(лЧс).
Реакции п-го порядка. В общем случае для реакции порядка п при п > 1 связь между концентрацией и временем для конечного времени наблюдения описывается уравнением
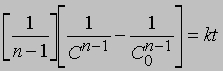
где С - концентрация реагента в момент времени t, C0 - начальная концентрация. График зависимости 1/(Сn - 1) от t представляет собой прямую с наклоном (n-1) k. Размерность k - (моль/л)1 - n/c. Реакции не всегда имеют целочисленный порядок. Показатели степени при концентрациях в выражении для скорости часто являются дробными. Однако и в этом случае порядок реакции равен сумме показателей степеней. Например, для реакции, скорость которой равна
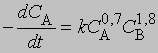
порядок п = 0,7 + 1,8 = 2,5. Часто порядок реакции, определяемый экспериментально, не соответствует порядку, который следует из стехиометрического уравнения. Большинство химических реакций включает две или несколько стадий, протекающих одновременно, что приводит к более сложным выражениям для скорости.
Определение порядка реакции. Подстановка в формулы. Если k остается постоянной при подстановке значений концентрации и времени в уравнение скорости реакции, значит, порядок реакции, задаваемый уравнением, верен. Если же расчеты не согласуются с экспериментальными данными, то реакция сложнее, чем предполагалось, и, вероятно, протекает в две или несколько стадий.
Графический метод. Для определения порядка реакции можно прибегнуть к графическому представлению функций, описывающих зависимость концентрации от времени. Если при построении зависимости С от t получается прямая, это означает, что реакция - нулевого порядка. Если линейна зависимость lg C от t, имеет место реакция первого порядка. При условии что начальная концентрация всех реагентов одинакова, реакция имеет второй порядок, если линейным является график зависимости 1/С от t, и третий - в случае линейности зависимости 1/С 2 от t.
Определение времени полупревращения. Для реакции первого порядка время, за которое прореагирует определенная часть реагента (например, половина), не зависит от начальной концентрации (см. выше),
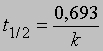
Для реакции второго порядка при равенстве начальных концентраций обоих реагентов, а = b, время, за которое прореагирует половина вещества, обратно пропорционально начальной концентрации. Из приведенного выше выражения для константы скорости реакции второго порядка получаем
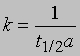
или
t1/2 = 1/ka
Изменение соотношения между реагентами. Если выражение для скорости представить как
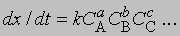
где СА, СВ, СС ... - концентрации участвующих в реакции веществ А, В и С ..., а а, b, с ... - соответствующие показатели степени в уравнении для скорости, то порядок реакции п можно определить, увеличив вдвое значение СА без изменения СВ и СС и экспериментально определив величину Dx/Dt для СА и 2СА. Так, если
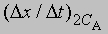
скорость при концентрации 2СА, а
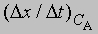
- скорость при концентрации СА, то, взяв отношение этих двух величин, получим
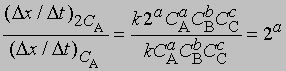
Предположим, что наблюдаемое отношение
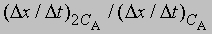
равно 4; тогда а = 2 и реакция является реакцией второго порядка относительно реагента А. Если это отношение равно 2, то а = 1 и имеет место реакция первого порядка относительно того же реагента. Аналогичным образом определяют b, с и т.д.
Добавление избытка реагентов. Добавив в реакционную смесь в большом избытке все реагирующие вещества, кроме одного, можно определить порядок реакции по этому реагенту, т.е. показатель степени, с которым концентрация данного реагента входит в уравнение скорости. Таким же образом определяют порядок реакции по каждому реагенту. Показатель степени для концентрации реагента А, не находящегося в избытке, устанавливают по графику зависимости dCA/dt от ln CA согласно уравнению
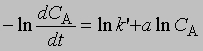
Наклон полученной прямой равен а. Константа kў является произведением константы скорости на концентрации реагентов, находящихся в избытке, взятые в соответствующих степенях. Молекулярность реакции определяется числом молекул, участвующих в самой медленной, лимитирующей стадии. Реакции бывают моно-, би-, три- и т.д. молекулярными. Порядок реакции и ее молекулярность не всегда можно предсказать исходя из стехиометрии реакции; для этого нужно провести кинетические измерения. В некоторых случаях порядок и молекулярность реакции, определенные исходя из ее стехиометрии, совпадают. Мономолекулярной называется такая реакция, в которой лимитирующей стадией является превращение одной молекулы, например распад ее на составляющие (диссоциация молекул иода I2 -> 2I) или превращение в другую молекулу в результате внутримолекулярной перестройки:
Бимолекулярная реакция - это взаимодействие двух молекул (например, молекулярного водорода с молекулярным иодом, H2 + I2 (r) 2HI). Реакция, протекающая одновременно с участием трех молекул, называется тримолекулярной. Поскольку вероятность столкновения сразу трех молекул, да еще в правильной взаимной ориентации, очень мала, такие реакции происходят редко.
Механизм химических реакций. При изучении механизма любой химической реакции рассматривают столкновение между отдельными реагирующими частицами (классическая теория столкновений) и другие элементарные акты с участием этих частиц. Учитывается также взаимная пространственная ориентация (стереохимия) реагирующих молекул. Считается, что реакция проходит через образование промежуточного комплекса, и для установления ее механизма необходимо знать состав и геометрию этого комплекса - межатомные расстояния и валентные углы. Реакции, называемые цепными, протекают через последовательность стадий. Продолжение цепи инициируют высокоэнергетические атомы или свободные радикалы. Рассмотрим фотохимическую реакцию образования хлороводорода. Под действием света молекула хлора распадается с образованием атомарного хлора. Атомы хлора реагируют с молекулой водорода с образованием HCl и атомарного водорода. Последний реагирует с молекулой хлора, вновь образуя HCl и высвобождая атом хлора:
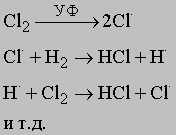
(точкой в верхнем индексе обозначается неспаренный электрон в валентной оболочке атомов; этим подчеркивается, что атомы и являются высокоактивными свободными радикалами). Иногда эта цепь взаимодействий продолжается до тех пор, пока не прореагируют более миллиона молекул на каждый образовавшийся при фотодиссоциации атом хлора. Если два атома, ответственные за рост цепи (и ),прореагируют друг с другом с образованием НCl или если один из них потеряет энергию в результате столкновений со стенками реактора либо с посторонними частицами, цепь прервется. Важным параметром, определяющим скорость газофазных реакций, является число столкновений между молекулами в единицу времени, которые имеют подходящую ориентацию и обладают достаточной для вступления в реакцию энергией. Частота и энергия соударений зависят от размера частиц и их средней скорости. В качестве иллюстрации того, как с помощью кинетических данных можно получить информацию о механизме химических реакций, рассмотрим образование HI и HBr: H2 + I2 = 2HI и H2 + Br2 = 2HBr
Стехиометрические уравнения этих реакций идентичны. Однако кинетические измерения скоростей реакций показывают, что их механизмы совершенно различны. Для первой реакции, в которой происходит столкновение молекул водорода и иода, увеличение концентрации HI во времени определяется уравнением d[[HI]]/dt = k[[H2]][[I2]] где [[H2]] и [[I2]] - молярные концентрации водорода и иода, k - константа скорости реакции. В то же время, как показывают кинетические измерения, увеличение во времени концентрации HBr следует уравнению
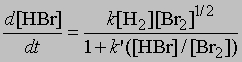
где [[H2]], [[Br2]] и [[HBr]] - молярные концентрации водорода, брома и бромоводорода, k и k' - константы. Реакция идет по цепному механизму, аналогичному тому, в соответствии с которым реагируют между собой хлор и водород с образованием хлороводорода: Br2 = 2Br, Br + H2 = HBr + H, H + Br2 = HBr + Br и т.д.
Выражение для скорости полной реакции можно получить, используя уравнения скоростей каждой из ее стадий. Температурные коэффициенты скоростей реакций. В диапазоне температур, близких к комнатной, скорость многих реакций удваивается или утраивается при повышении температуры на каждые 10°. С.Аррениус предложил следующее уравнение, описывающее зависимость константы скорости реакции от температуры: k = s exp(-DHa/RT)
Предэкспоненциальный множитель s называется аррениусовским частотным фактором и в бимолекулярной реакции определяется частотой столкновений молекул, которые имеют подходящую ориентацию для того, чтобы вступить в химическое взаимодействие, DНа - теплота (или энтальпия) активации, R - универсальная газовая постоянная [[1,987 кал/(град*моль), если DНа выражается в кал/моль]]. DНа равна кинетической энергии, которой должны обладать сталкивающиеся частицы, чтобы преодолеть их взаимное отталкивание и образовать продукты. Уравнение Аррениуса можно записать в дифференциальной форме:
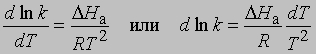
Интегрирование в предположении, что DНа не зависит от Т, дает
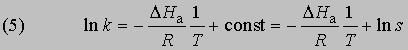
откуда
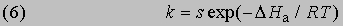
Интегрирование в предположении независимости DНа от Т дает
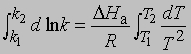
или
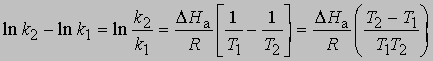
Из уравнения (5) следует, что график зависимости ln k от 1/Т является прямой с наклоном -DНа/R, откуда DНа можно определить как -RЧs (где s - тангенс наклона прямой). Используя данное значение DНа и значение k при одной температуре, можно найти частотный фактор и затем рассчитать k при любой другой температуре из температурного диапазона, в котором сохраняется постоянной величина DНа. Член ln s в уравнении Аррениуса можно также определить графически, экстраполяцией графика зависимости ln k от 1/T к 1/Т = 0. В этой точке ln k = ln s (рис. 2).
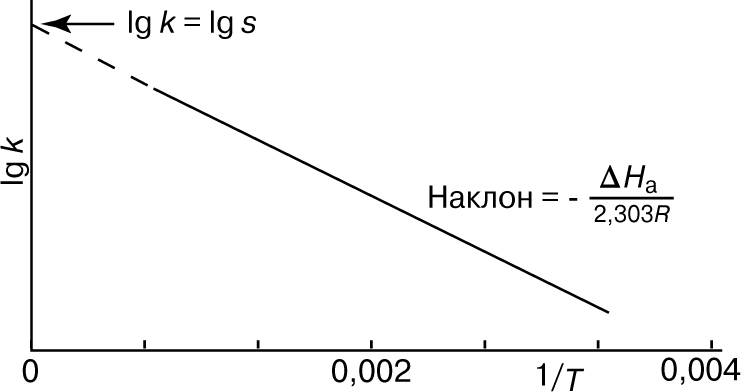
Рис. 2. ГРАФИК ЗАВИСИМОСТИ логарифма k от 1/Т.
Экспоненциальный член exp(-DНа/RT) в уравнении (6) равен доле молекул с энтальпией , т.е. молекул, обладающих достаточной энергией, чтобы вступить в реакцию. Для бимолекулярных реакций аррениусовский частотный фактор можно представить как число столкновений в единицу времени в единице объема между молекулами, имеющими нужную ориентацию. Таким образом, k определяется числом столкновений химически активных и ориентированных нужным образом молекул. В рамках теории абсолютных скоростей реакций (или термодинамической теории) частотный фактор можно представить как
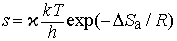
где x - трансмиссионный коэффициент, представляющий собой долю молекул, энергия которых превышает энергетический барьер на пути перехода от реагентов к продуктам, k - константа Больцмана, h - постоянная Планка, DSа - энтропия активации на моль реагента. DSа является мерой относительного числа степеней свободы молекул в активированном и исходном состояниях (т.е. числа независимых типов колебаний и вращений). Для некоторых мономолекулярных газофазных реакций распада активированный комплекс настолько близок по своей структуре к исходным реагентам, что изменение энтропии очень мало, т.е. DSа можно принять равным нулю. В этих случаях
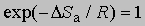
,
и если x = 1, то константа скорости реакции определяется выражением
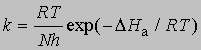
При 27° С (300 К)
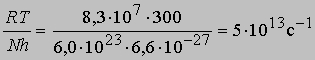
(N - число Авогадро). Отсюда получаем приближенное уравнение для мономолекулярных реакций:
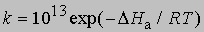
и менее точное уравнение для бимолекулярных реакций:
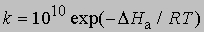
где 10 10 в первом приближении равно числу столкновений молекул при комнатной температуре, если концентрации выражены в моль/л.
ХИМИЧЕСКОЕ РАВНОВЕСИЕ
Обратимость и равновесие. Обратимая химическая реакция - это реакция, в ходе которой происходят превращения как в прямом, так и в обратном направлениях. Первым, кто четко сформулировал представление об обратимости химических реакций, был К.Бертолле (1799). Участвуя в Египетской экспедиции Бонапарта, он обратил внимание на образование карбоната натрия в соляных озерах и пришел к заключению, что карбонат натрия образуется в результате взаимодействия между насыщенным раствором хлорида натрия и растворенным карбонатом кальция. Этот процесс обратен проводимой в лаборатории реакции между карбонатом натрия и растворенным хлоридом кальция с образованием карбоната кальция. В 1864 К.Гульдберг и П.Вааге открыли закон действующих масс, согласно которому скорость химической реакции прямо пропорциональна концентрации реагирующих веществ. Положение равновесия можно определить, зная скорости прямой и обратной реакций. Уравнение обратимой реакции имеет вид
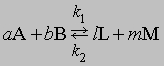
Если СА, СВ, СL и СМ - молярные концентрации веществ А, В, L и М; а, b, l и m - соответствующие стехиометрические коэффициенты, k1 и k2 - константы скорости прямой и обратной реакций, то
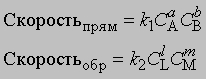
В равновесии скорости прямой и обратной реакций равны:
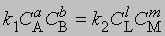
и
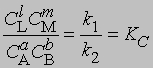
где С - равновесная концентрация соответствующего вещества, KС - константа химического равновесия, выраженная через концентрации. Более строгий подход к выводу выражения для константы равновесия основан на принципах термодинамики. Можно показать, что в условиях равновесия (при равновесных концентрациях реагентов и продуктов) стандартное изменение свободной энергии системы определяется уравнением
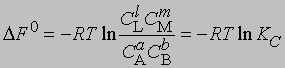
Поскольку DF0 при постоянной температуре является константой, то и KС тоже константа, равная
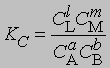
Для газофазных реакций константу равновесия можно выразить через парциальные давления реагентов:
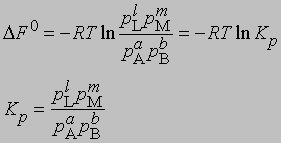
Представленная таким образом константа равновесия отличается от KС, выраженной через молярные концентрации, соответственно различаются и DF0 для этих двух случаев. Поясним, что такое изменение свободной энергии DF0 в ходе химической реакции. При постоянных температуре и давлении уменьшение свободной энергии является максимальной работой, которую можно совершить в ходе процесса, причем эта работа не связана с изменением объема или давления в системе. Стандартное изменение свободной энергии DF0 равно разности свободных энергий реагентов и продуктов в стандартных состояниях. Такое состояние для идеального газа - давление 1 атм, а для твердых веществ или жидкостей - их наиболее стабильная форма при давлении 1 атм и определенной температуре. Для идеального растворенного вещества стандартным является состояние при концентрации 1 моль на 1000 г растворителя (моляльная концентрация). Для газофазных реакций KС можно связать с Kр, используя уравнение состояния идеального газа: C = 1/V = p/RT
где V - объем, занимаемый одним молем газа, R - газовая постоянная, Т - абсолютная температура,
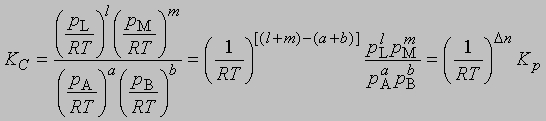
где Dn = (l + m) - (a + b) разность между суммой молей продуктов реакции и суммой молей исходных реагентов; эта разность определяется коэффициентами стехиометрического уравнения реакции. Следует иметь в виду, что DF0 - это разность свободных энергий реагентов и продуктов в их стандартных состояниях, а именно при концентрации растворенных веществ 1 М и давлении газов 1 атм, а рассчитывается эта разность свободных энергий по данным для равновесных концентрации и давления.
Равновесие в газофазных системах. Рассмотрим диссоциацию N2O4 (тетраоксид диазота) на две молекулы диоксида азота (NО2). Мол. масса N2O4 равна 92; это бурый газ с т. кип. 21,3° С. При нагревании цвет газа меняется до черного. При температуре 140° С происходит полная диссоциация N2O4 на NO2 с мол. массой 46 в соответствии с уравнением

Пусть a - мольная доля газа, подвергшегося диссоциации, а из каждого моля получается n молей газообразных продуктов; тогда общее число молей газа будет равно 1 - a + na = 1 + (n - 1)a
Плотность данной массы газа при постоянном давлении обратно пропорциональна числу молей. Обозначим через d1 плотность недиссоциированного газа, а через d2 - плотность смеси исходного и диссоциированного газа при том же давлении. Тогда
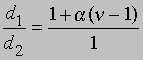
и
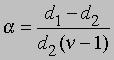
Заменив плотности на мол. массы, получим
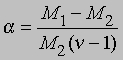
где М1 - мол. масса недиссоциированного газа, М2 - средняя мол. масса смеси исходного и диссоциированного газа. Поскольку для данной реакции n = 2 и общее число молей газа в смеси равно 1 - a + 2a = 1 + a, парциальные давления N2O4 и NO2 равны соответственно
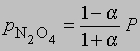
и
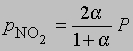
где Р - суммарное давление. Теперь
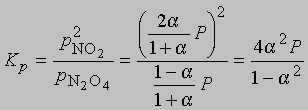
Если доля диссоциированного газа при 75° С равна 0,741 и суммарное давление 1 атм, то
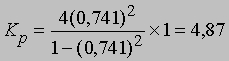
Отметим, что при повышении суммарного давления степень диссоциации будет уменьшаться в соответствии с уравнением (7) и принципом Ле Шателье, согласно которому система стремится сохранить состояние, в котором она находится, в противовес любым внешним воздействиям. Приведем в качестве примера несколько изученных газофазных реакций: N2 + 3H2 2NH3 H2 + I2 2HI N2 + O2 2NO CO2 + H2 CO + H2O В последних трех случаях изменение давления в системе не повлияет на ход реакции, поскольку число молекул исходных соединений и продуктов одинаково. Однако в первом случае при повышении давления будет наблюдаться ускорение процесса - образование большего количества продукта.
Равновесие в гомогенной жидкой системе. Одним из типичных примеров обратимой реакции в гомогенной жидкой системе является реакция между уксусной кислотой и этиловым спиртом с образованием этилацетата и воды:
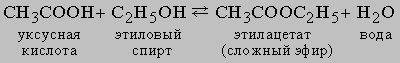
Константа равновесия KС этой реакции равна
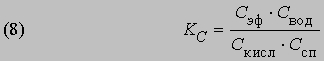
Если а молей кислоты и b молей спирта в смеси с l молями этилацетата и m молями воды образуют раствор объемом v и если x молей кислоты и x молей спирта дают x молей этилацетата и x молей воды, то можно записать уравнение (8) в следующем виде:
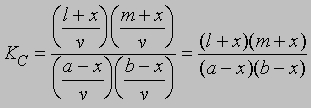
Разные электролиты диссоциируют в полярных растворителях в разной степени (см. ЭЛЕКТРОЛИТЫ). Для определения степени диссоциации электролитов чаще всего применяют достаточно простой и точный метод, основанный на измерении их электропроводности. Согласно Аррениусу, степень диссоциации электролита равна
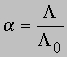
где A - эквивалентная электропроводность (т.е. проводимость, соответствующая одному "молю" заряда) электролита, концентрацию которого хотят определить, L0 - эквивалентная электропроводность электролита при бесконечном разбавлении, когда он полностью диссоциирован. Зная концентрацию и степень диссоциации, можно определить константу ионизации (для кислот - константу протолиза) слабого электролита. Обычно ионизация или диссоциация подавляется при добавлении в среду избытка продукта диссоциации. Кислота, образующаяся при захвате протона данным основанием, называется кислотой, сопряженной с этим основанием; соответственно основание, образующееся при отдаче протона данной кислотой, называется основанием, сопряженным с этой кислотой. Представим протолиз (или ионизацию кислоты в воде) как взаимные превращения сопряженных кислот и оснований: HA + H2O H3O+ + A-где НА и А- сопряженные кисло