гидроаэро́бика, -и
гидроаэродром
Толковый словарь
м.
Акватория с прилегающей прибрежной территорией и комплексом необходимых сооружений, предназначенная для взлета, посадки, размещения гидросамолетов.
Энциклопедический словарь
ГИДРОАЭРОДРО́М -а; м. Акватория с прилегающей прибрежной территорией и комплексом необходимых сооружений для взлёта, посадки и размещения гидросамолётов.
Академический словарь
Слитно. Раздельно. Через дефис
Орфографический словарь
Синонимы к слову гидроаэродром
Морфемно-орфографический словарь
Новый словарь иностранных слов
гидроаэродро́м
(см. гидро... + аэродром) участок водной поверхности (акватория) с прилегающей к нему территорией на берегу и комплексом технических сооружений, предназначенный для взлета, посадки, якорной стоянки и технического обслуживания гидросамолетов.
Сканворды для слова гидроаэродром
- Акватория с прилегающей прибрежной территорией и комплексом необходимых сооружений, предназначенная для взлёта, посадки, размещения гидросамолётов.
Полезные сервисы
гидроаэроионизатор
Синонимы к слову гидроаэроионизатор
Сканворды для слова гидроаэроионизатор
Полезные сервисы
гидроаэроионизация
гидроаэроионотерапия
гидроаэромеханика
Толковый словарь
ж.
Раздел механики, изучающий равновесие и движение жидких и газообразных сред и их взаимодействие между собою и с твёрдыми телами.
Энциклопедический словарь
ГИДРОАЭРОМЕХА́НИКА -и; ж. Раздел механики, изучающий равновесие и движение жидких или газообразных сред и их взаимодействие между собой и с твёрдыми телами.
Академический словарь
-и, ж.
Раздел механики, посвященный изучению равновесия и движения жидких и газообразных сред и их взаимодействия между собой и с твердыми телами.
Энциклопедия Кольера
ГИДРОАЭРОМЕХАНИКА - раздел механики, изучающий движение жидкостей и газов в условиях, при которых не имеют практического значения различия в сжимаемости. Такой единый подход возможен, поскольку благодаря своей текучести жидкие и газообразные среды ведут себя одинаково до тех пор, пока силы, характерные для газообразного состояния вещества, не приводят к заметным изменениям его объема. Поэтому одни и те же законы применимы в столь различных областях науки и техники, как вентиляционная техника и гидравлика, метеорология и океанография, авиация и кораблестроение. Гидроаэромеханика отличается как от эмпирической гидравлики, так и от математической гидродинамики, поскольку она не только основывается на твердо установленных законах физики, но и опирается на опытные данные, проверяя и дополняя ими теоретический анализ. Измерение движения жидкостей и газов. Единицы. Движение жидкостей и газов, как и все другие виды движения, рассматриваемые в механике, можно полностью охарактеризовать, оперируя единицами измерения длины, времени и силы. Так, диаметр парашюта можно измерять в метрах, время снижения, скажем, на 100 метров - в секундах, а вес груза - в ньютонах. Точно так же входное сечение насоса можно измерять в квадратных метрах, объемный расход среды - в кубических метрах в секунду, а мощность - в ньютон-метрах (джоулях) в секунду. Существует много способов измерения таких характеристик течения с использованием различных - механических и электрических - эквивалентов линейки, часов и пружинных весов. Например, скорость жидкостей и газов можно оценивать по числу оборотов в единицу времени проградуированной крыльчатки (гидрометрическая вертушка и анемометр) или по изменению электросопротивления нагреваемой проходящим током проволоки (проволочный термоанемометр); давление можно определять по вызываемому им отклонению изогнутой трубки или мембраны (манометр Бурдона и барометр-анероид) либо по току, генерируемому пьезокристаллом.
Прогнозирование характеристик течения. Если бы такие измерения движения жидкостей и газов были единственным занятием гидроаэромеханики, это была бы дисциплина довольно узкого профиля. Гораздо более важное значение, чем измерение, имеет точное прогнозирование характеристик течения при заранее известных или предполагаемых условиях. Очевидно, что недостаточно уметь просто измерить пропускную способность построенного водослива, - нужно сначала надежно спроектировать водослив, рассчитанный на максимально возможный поток; точно так же измерить лагом скорость судна в плавании проще, чем заранее указать мощность двигателей, которые потребуются новому судну для поддержания заданной крейсерской скорости; напечатать в газете скорость ветра и атмосферное давление, измеренные вчера, гораздо легче, чем предсказать погодные условия на завтрашний день. Короче говоря, истинный предмет гидроаэромеханики - установление соотношений между различными характеристиками течения, позволяющих определить любую из них, коль скоро заданы другие характеристики, от которых она зависит.
АНАЛИЗ ТЕЧЕНИЯ ЖИДКОСТЕЙ И ГАЗОВ
Картина течения. Первый шаг в решении любой задачи о движении жидкости или газа - наглядное представление картины течения. Можно представить себе ряд тонких струек (линий) движущейся среды так, что в каждой своей точке они совпадают с направлением течения. Такие линии называются линиями тока. Если течение установившееся, т.е. картина течения со временем не меняется, то линии тока совпадают с траекториями частиц текущей среды. Течение называется равномерным, если все линии тока прямолинейны и параллельны (рис. 1). Течение через водослив является установившимся - все линии тока в нем совпадают с траекториями частиц, взвешенных в воде. Но такое течение нельзя считать равномерным, поскольку линии тока искривлены и сгущаются при переходе через гребень водослива. Течение, вызываемое движущимся телом, например кораблем, тоже неравномерно, так как корабль все время меняет свое положение и траектории частиц воды лишь кратковременно совпадают с линиями тока (рис. 2). Движение такого вида, неустановившееся и неравномерное, представляется очень сложным для наблюдателя. Но оно выглядело бы гораздо проще, если бы наблюдатель мог двигаться с той же скоростью, что и корабль, так как тогда он видел бы движение, по крайней мере перед кораблем, в установившихся условиях и линии тока совпадали бы с траекторией движения. Такое упрощение задачи основано на представлении об относительном движении, которое часто оказывается полезным в механике. Если бы к тому же течение зависело только от формы границы, в данном случае от формы передней части корабля, то линии тока можно было бы построить у контура этой границы с использованием графических, механических или электрических процессов, описываемых математическим соотношением между этим контуром и картиной потока.
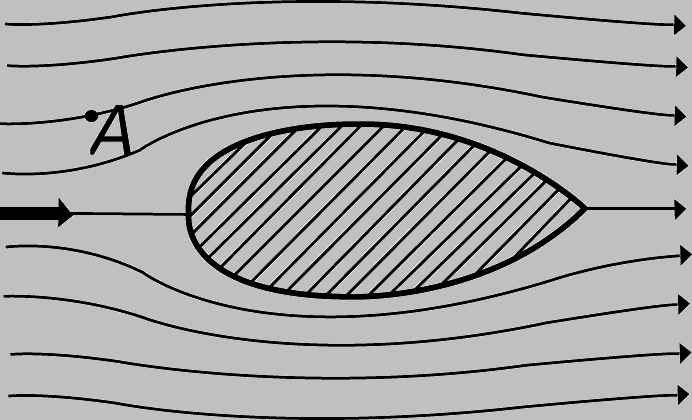
Рис. 1. КАРТИНА УСТАНОВИВШЕГОСЯ ТЕЧЕНИЯ вокруг неподвижного тела обтекаемой формы.
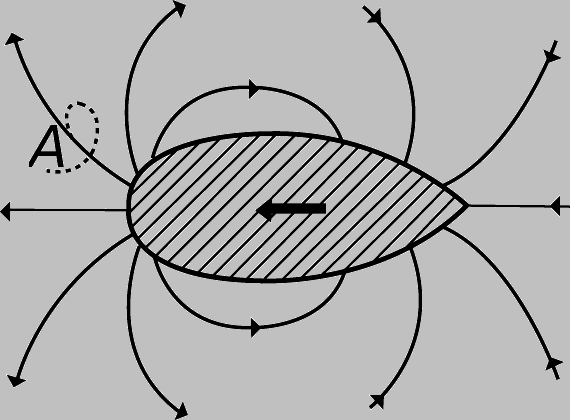
Рис. 2. КАРТИНА НЕУСТАНОВИВШЕГОСЯ ТЕЧЕНИЯ вокруг движущегося тела обтекаемой формы.
Уравнение неразрывности. Соотношение между скоростью течения, объемным расходом среды и расстоянием между линиями тока называется уравнением неразрывности. Это уравнение выражает один из основных законов гидроаэромеханики, согласно которому объемный расход во всякой трубке тока, ограниченной соседними линиями тока, должен быть в любой момент времени одинаков во всех ее поперечных сечениях. Поскольку объемный расход Q равен произведению скорости текущей среды V на площадь A поперечного сечения трубки тока, уравнение неразрывности имеет следующий вид:
Q = V1A1 = V2A2.
Поэтому там, где сечение велико и линии тока разрежены, скорость должна быть мала, и наоборот. (Все три части этого двойного равенства должны выражаться в одной и той же системе единиц. Так, если величина Q выражена в м3/с, то скорость V должна выражаться в м/с, а площадь A - в м2.)
Закон сохранения энергии. Если текущая среда движется с ускорением, то, согласно законам Ньютона, это означает, что на среду действует некая сила в направлении ускорения. Сила, действующая на единицу объема, должна быть равна произведению ускорения на массу этой единицы объема. Таким образом, динамика течения определяется по крайней мере одной характеристикой среды - плотностью r и по крайней мере одним видом сил, действующих в среде, - обусловленных разностью давлений в двух соседних точках линии тока. Если плотность - единственная характеристика, которую нужно учитывать, а изменения давления от точки к точке в среде - единственный вид действующих сил, то можно написать уравнение второго закона Ньютона, которое связывает плотность с изменением давления, в довольно сложной дифференциальной форме т.н. уравнения Эйлера. Будучи проинтегрировано вдоль трубки тока, оно дает очень простую и полезную формулу:
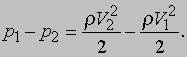
Это уравнение выражает тот факт, что изменение скорости в промежутке между двумя поперечными сечениями трубки тока в условиях неравномерного течения сопровождается соответствующим изменением давления, причем давление понижается с увеличением скорости, и наоборот. Поскольку левая часть уравнения выражает работу, совершаемую над единичным объемом среды при перемещении на единичное расстояние, а правая - соответствующее изменение его кинетической энергии, это уравнение представляет собой закон сохранения энергии. Оно применимо только в случае установившегося течения.
Закон сохранения количества движения. Несколько иной путь решения того же самого дифференциального уравнения приводит к столь же простой и полезной формуле Fx = Qr (V2 - V1)x, которая показывает, что внешняя сила, действующая на участок трубки тока в заданном направлении (скажем, в направлении x), пропорциональна изменению скорости в этом направлении. Поскольку в правой части стоит скорость изменения количества движения среды под действием этой силы, данное уравнение выражает закон сохранения количества движения (импульса). Оно позволяет объяснить принцип реактивного движения. Если некое тело выбрасывает высокоскоростную струю газа (или жидкости), то эта струя действует на тело с силой F, равной изменению ее количества движения, что и заставляет его двигаться.
ФАКТОРЫ, ВЫЗЫВАЮЩИЕ ИЗМЕНЕНИЕ ТЕЧЕНИЯ
Уравнение неразрывности, законы сохранения энергии и количества движения в представленном выше простом виде позволяют приближенно решать многие практические задачи, связанные с течением. К ним относятся задачи о силах воздействия струи на обтекаемое тело (крыло, руль, лопасть), о скорости истечения из сопел и диафрагм на концах напорных линий, о соотношении между давлением и скоростью для таких измерительных устройств, как расходометр Вентури и трубка Пито, и о реакции текущей среды на изгибы трубопровода и на изменения площади его поперечного сечения. В каждой такой задаче предполагается, что картина течения полностью определяется формой его границ; причиной изменения картины течения может быть влияние таких факторов, как вес, вязкость текущей среды, завихрения и сжимаемость.
Вес. Уравнение Бернулли. Самая простая после плотности характеристика текущей среды - это, пожалуй, удельный вес g, т.е. вес единицы объема среды. (Отношение g к r равно ускорению силы тяжести g.) Если ввести эту величину в основные уравнения движения, то уравнения непрерывности и закона сохранения количества движения не изменятся, а уравнение закона сохранения энергии примет следующий вид:
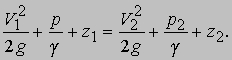
Это т.н. уравнение Бернулли. Все его слагаемые имеют размерность длины; первое слагаемое в обеих частях равенства называется скоростным напором, а второе - гидростатическим напором; z - высота расположения трубки тока в данной точке, измеренная относительно некоего уровня отсчета (рис. 3). Согласно уравнению Бернулли, в случае установившегося течения, для которого не имеют существенного значения все другие характеристики текущей среды, кроме плотности (удельного веса), полный напор одинаков во всех поперечных сечениях трубки тока. Если к отверстию в стенке трубы присоединить манометрическую трубку, то жидкость в такой трубке поднимется на высоту, равную гидростатическому напору. Если манометрическую трубку выставить навстречу потоку, то жидкость в манометре поднимется на дополнительную высоту, равную скоростному напору. Трубка, имеющая одновременно торцевое и боковые манометрические отверстия, называется трубкой Пито (рис. 4) и используется для определения скорости течения по измеренному скоростному напору. Трубки Пито входят в комплект измерительного оборудования всех самолетов, а также широко применяются для измерений скорости течения в трубопроводах, вентиляционных воздуховодах, в аэро- и гидродинамических трубах.
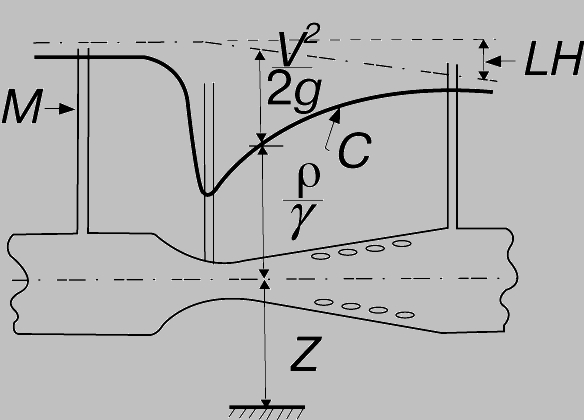
Рис. 3. ИЗМЕНЕНИЕ НАПОРА вдоль оси расходомера Вентури. М - манометр, показывающий гидростатический напор: С - кривая изменения гидростатического напора; LH - потеря напора, обусловленная трением.

Рис. 4. ТРУБКА ПИТО. DF - патрубок для присоединения дифференциального манометра, измеряющего скоростной напор.
Если скорость течения равна нулю (т.е. среда не движется), то уравнение Бернулли сводится к простому уравнению гидростатики
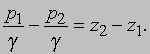
Согласно этому уравнению, увеличению высоты в неподвижной среде жидкости или газа соответствует равное уменьшение гидростатического напора. Поэтому давление в любой точке неподвижной жидкости равно глубине этой точки под свободной поверхностью, умноженной на удельный вес жидкости. На основе этого соотношения вычисляется давление жидкости на стенки резервуаров, а также проводится анализ плавучести и остойчивости морских и речных судов. В тех случаях, когда скорость течения отлична от нуля, уравнение Бернулли совместно с уравнениями неразрывности и закона сохранения количества движения позволяет решать практически важные задачи - о расходе среды, текущей через измерительные диафрагмы, поверх измерительных и водосбросных водосливов и под затворы шлюзовых галерей; о траектории струи жидкости; о форме, скорости и силе волн, действующих на суда и волноломы. Хотя в таких задачах обычно рассматривается течение воды под атмосферным слоем воздуха, аналогичные процессы гравитационного характера имеют место в случае течения более холодной (и, следовательно, более плотной) воды под более теплой, как и других жидкостей и газов разной плотности. Таким образом, водным потокам в реках аналогичны океанские течения и ветры, поскольку все гравитационные явления подчиняются одним и тем же законам гидроаэромеханики.
Гравитационное моделирование. Число Фруда. Хотя многие задачи такого рода решаются с приемлемой точностью, существует много других сложных задач, аналитическое решение которых пока невозможно. Тем не менее удовлетворительное решение ряда таких задач можно находить путем моделирования с использованием теории подобия. Влияние силы тяжести на картину потока характеризуется безразмерной величиной (критерием подобия), составленной из некой характерной скорости V, характерной длины L, разности Dg удельных весов верхней и нижней текущих сред и плотности r одной из них:
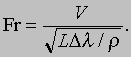
Эта величина называется числом Фруда. Очевидно, что в случае течения воды под атмосферным воздухом мы имеем просто . Подобие будет обеспечено только в том случае, если число Фруда для модели равно числу Фруда для реального объекта (т.е., например, скорость модели судна должна быть уменьшена пропорционально квадратному корню из уменьшения размера). Такого рода экспериментальные исследования уменьшенных моделей - обычная практика при проектировании судов и речных гидротехнических сооружений; более того, в настоящее время методы моделирования распространяются на аналогичные гравитационные задачи метеорологии и океанографии.
Вязкость. Формулы Пуазейля и Стокса. Задачи, в которых существенна только динамическая вязкость m, в ряде частных случаев могут быть полностью решены аналитически, если исходить из того, что скорость вязкой текучей среды в точке соприкосновения с твердой границей такая же, как и скорость границы, т.е. равна нулю, если та неподвижна. Типичные примеры такого решения - формула Пуазейля для перепада давления, необходимого для поддержания вязкого течения в малой трубке постоянного диаметра D длиной L:
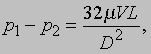
и формула Стокса для силы сопротивления вязкой среды медленному движению очень малого шарика диаметром D: F = 3pmVD.
(Величина m для воздуха равна приблизительно 0,018*10-3, для воды ГИДРОАЭРОМЕХАНИКА10-3 и для глицерина ГИДРОАЭРОМЕХАНИКА1500 * 10-3 Па*с.)
Число Рейнольдса. Во всех рассмотренных выше случаях плотность текучей среды, очевидно, не играет роли, поскольку силы, вызывающие ускорение среды, либо отсутствуют, либо пренебрежимо малы по сравнению с силами вязкого сдвига. Но если бы труба была большой длины и переменного диаметра, а шарик двигался с большой скоростью, то эффекты, связанные с ускорением, были бы значительны и плотность в уравнениях движения нельзя было бы опускать. Однако тогда эти уравнения были бы слишком сложны, а потому снова приходится прибегать к критерию подобия, характеризующему влияние вязкости на картину течения. Этот критерий имеет вид
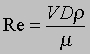
и называется числом Рейнольдса. Оно играет такую же роль в моделировании влияния вязкости, что и число Фруда при моделировании гравитационных эффектов, а потому служит основой опытов, проводимых в аэродинамических трубах с моделями самолетов, и градуировок расходомеров для жидкостей разной вязкости - в общем, при исследовании всех видов течений по трубам и с обтеканием тел во всех случаях, когда доминирует влияние вязкости. Если равенство чисел Фруда для модели и натурного объекта, как мы видели, требовало уменьшения скорости модели в связи с ее уменьшенными размерами, то равенство чисел Рейнольдса, наоборот, требует, чтобы скорость модели увеличивалась с уменьшением ее размеров. Поэтому, чтобы не нужно было чрезмерно повышать скорость в экспериментах с уменьшенными моделями, часто применяют текучие среды с меньшей вязкостью или большей плотностью; так, в аэродинамических трубах нередко повышают давление до нескольких атмосфер, что позволяет снизить скорость за счет повышения плотности.
Турбулентное течение в трубах. Течение вязкой жидкости вдоль границы может оказаться неустойчивым по отношению к малым возмущениям, если число Рейнольдса превысит некоторое значение. Так, например, течение в трубе постоянного диаметра устойчиво ко всем возмущениям, если число Рейнольдса VDr/m меньше приблизительно 2000, и тогда формула Пуазейля дает соотношение между перепадом давления и скоростью независимо от плотности. Но когда число Рейнольдса превышает указанное критическое значение, любое локальное возмущение вызывает колебания скорости или образование завихрений, которые быстро распространяются по всему потоку, создавая беспорядочное вторичное движение, называемое турбулентным течением. Из-за бесчисленных вихрей турбулентное течение характеризуется значительно большей затратой энергии (более высокими потерями давления), чем устойчивое, или ламинарное, течение, и формула Пуазейля в этом случае заменяется формулой
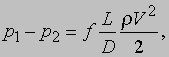
где коэффициент f зависит от числа Рейнольдса и относительной шероховатости поверхности трубы. В случае гладкой трубы, например, f = 0,316/Re1/4, тогда как при аналогичных условиях формула Пуазейля дает f = 64/Re. Чем больше шероховатость поверхности, тем, очевидно, больше величина f ; если шероховатость трубы достаточно велика, то при больших числах Рейнольдса коэффициент f перестает зависеть от вязкого сдвига и полностью определяется неровностями стенок, вызывающих завихрения.
Явления в пограничном слое. В случае течения указанного вида по длинной трубе влияние стенок на характер течения распространяется и на центральную часть трубы. В случае же обтекания тела средой замедляющее действие вязкого сдвига вдоль поверхности тела (на которой скорость равна нулю) обычно распространяется в окружающую среду лишь на сравнительно небольшое расстояние. Относительная толщина этого т.н. пограничного слоя зависит от числа Рейнольдса, составленного из относительной скорости, плотности и вязкости текучей среды и расстояния от рассматриваемой точки до передней кромки тела. При малых значениях Re пограничный слой будет ламинарным, но течение становится неустойчивым по отношению к малым возмущениям, когда Re приближается к 4Ч106, а после этого развивается турбулентность. Вязкий сдвиг вдоль граничной поверхности теперь аналогичен перепаду давления вдоль трубы и точно так же зависит от числа Рейнольдса. Полная сила сопротивления течению FD, создаваемая участком поверхности длиной L и шириной B, дается выражением
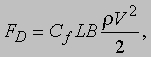
где Cf - коэффициент сопротивления, зависящий от Re = VLr/m и от шероховатости поверхности. Для гладкой поверхности Cf = 1,33/Re1/2, если пограничный слой ламинарный, и Cf = 0,074/Re1/5, если пограничный слой полностью турбулентный. Это соотношение играет очень важную роль в расчетах сопротивления крыла и фюзеляжа самолета, а также корпуса речного или морского судна. Теория пограничного слоя разработана Л.Прандтлем (1875-1953). Наряду с поверхностным сопротивлением, возникающим в пограничном слое, в этом слое наблюдается еще одно важное явление - отрыв течения от стенки при резком изменении ее геометрии. Вязкая текучая среда при больших числах Рейнольдса не следует точно за изломом стенки и не смыкается без возмущений даже позади хорошо закругленного тела, например сферического. Для предотвращения отрыва потока задней части тела придают обтекаемую форму и точно так же сглаживают (профилируют) трубу переменного диаметра (сопло Лаваля). Явление отрыва связано с высокими градиентами давления и скорости течения в пограничном слое, и такая тенденция заметно ослабевает, если отводить текучую среду из пограничного слоя. Поэтому, в частности, предусматривают прорези на крыльях и фюзеляже самолета для слива пограничного слоя. Отрыв потока, вообще говоря, нежелателен, поскольку он обычно возникает в точках максимальной скорости и, следовательно, минимального давления, после чего это низкое давление доминирует во всей зоне отрыва ниже по течению. В результате течение воздействует на поверхность тела (стенку) с некоторой силой, добавляющейся к поверхностному сопротивлению (создавая "сопротивление формы", обусловленное повышенным давлением спереди обтекаемого тела и пониженным - сзади), а энергия течения "непроизводительно" расходуется на интенсивную турбулентность, возникающую в неустойчивой зоне отрыва. Для погруженных в поток тел сочетание поверхностного сопротивления и сопротивления формы дает полную силу сопротивления движению, зависящую, таким образом, от формы тела и от числа Рейнольдса, а именно, если обозначить площадь поперечного сечения тела через A:
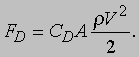
Для сферы при малых числах Рейнольдса (менее 1) формула Стокса принимает вид CD = 24/Re; при Re Ј 105 пограничный слой является ламинарным и CD = 0,5; при Re Ј 106 пограничный слой становится турбулентным и CD = 0,2. Для парашюта сопротивление должно быть максимальным и CD = 1,3, тогда как для высокоскоростного самолета коэффициент CD может составлять лишь 0,05.
Вихревые колебания. В случае удлиненных тел, скажем цилиндрических, закономерности сопротивления среды оказываются примерно такими же, как и для сфер, но, кроме того, происходят поперечные колебания зоны отрыва течения (рис. 5). Поскольку при этом зона пониженного давления оказывается то с одной, то с другой стороны от направления движения (вихревая дорожка фон Кармана), на тело действует не только продольная сила лобового сопротивления, но и переменная поперечная сила. Этим объясняются вибрация перископов высокоскоростных подлодок и гудение проводов при сильном ветре. Частота такой вибрации тоже зависит от числа Рейнольдса; например, для цилиндра при Re = 105 и ламинарном пограничном слое период колебаний t определяется равенством Vt/D = 5; когда же пограничный слой становится турбулентным, этот численный множитель уменьшается в два раза.
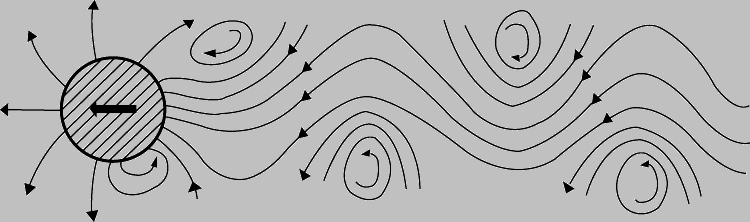
Рис. 5. ЗАВИХРЕНИЯ течения позади движущегося цилиндра.
Плоская поверхность. Сходную поперечную силу отрыв потока вызывает в случае плоской поверхности, наклоненной, подобно воздушному змею, относительно направления течения, но в этом случае боковая сила не меняет периодически своего направления. На тонкую пластину, находящуюся в потоке под углом атаки к нему, также действует заметная сила сопротивления, обусловленная понижением давления в зоне отрыва, но эту силу можно существенно уменьшить (при одновременном увеличении поперечной силы), если придать пластине утолщенный профиль, закругленный спереди и слегка искривленный ("вогнуто-выпуклый"). Такое тело, называемое аэродинамической поверхностью или попросту крылом, создает подъемную силу, за счет которой летают самолеты (теория крыла разработана русскими учеными Н.Е.Жуковским (1847-1921) и С.А.Чаплыгиным (1869-1942)), а в виде подводного крыла используется на скоростных речных и морских судах. Искусство проектирования таких профилей достигло столь высокого уровня, что легко обеспечиваются подъемные силы, в 30 и более раз превышающие лобовое сопротивление (рис. 6).
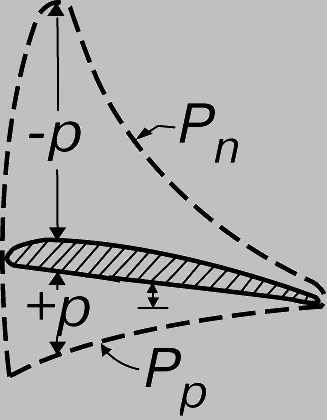
Рис. 6. РАСПРЕДЕЛЕНИЕ ДАВЛЕНИЯ вокруг аэродинамического профиля, движущегося справа налево: Pin - отрицательное давление на верхней поверхности; Pip - положительное давление на нижней поверхности; a - угол атаки.
Сила, действующая на крыло (или руль) в потоке, дается выражением
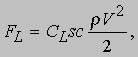
где s - размах (длина), а c - хорда (ширина) крыла. При больших числах Рейнольдса величина CL зависит практически только от формы и угла наклона профиля; приемлемой величиной для крыла можно считать CL = 0,5 .
Поверхности другой формы. Поверхности, создающие подъемную силу, используются в конструкциях крыла самолетов и других скоростных судов; на основе тех же принципов проектируются лопасти воздушных и гребных винтов, лопатки и лопасти рабочих колес турбин, насосов, компрессоров, гидродинамических передач. В испытаниях устройств и машин такого рода определяют коэффициенты тяги, всасывания, мощности (гребного винта), напора и подачи, аналогичные коэффициентам подъемной силы и лобового сопротивления для аэродинамической поверхности. Всякий такой коэффициент зависит от формы поверхности и от числа Рейнольдса, при котором она должна работать, и оценка этих коэффициентов по данным модельных экспериментов производится на основе тех же самых законов подобия. Важное значение имеет то обстоятельство, что рабочие характеристики любой модели можно, исходя из соображений удобства, изучать как в воде, так и в воздухе независимо от назначения проектируемого устройства при условии, что воспроизводится число Рейнольдса и другие определяющие критерии.
Сжимаемость. Хотя сжимаемость (или ее обратная величина - упругость) является свойством, которое, строго говоря, выводит нас за рамки гидроаэромеханики, ее, по крайней мере при упрощенной постановке задачи, приходится учитывать по соображениям двоякого рода. Во-первых, реальные жидкости и газы представляют собой упругие среды, и звуковые волны распространяются в них со скоростью, которая вычисляется по одной и той же формуле. Если скорость звука обозначить через с, а модуль упругости - через E, то формула запишется в виде
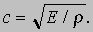
(Скорость звука с в воздухе составляет 335, а в воде - около 1430 м/с.) Если течение в трубопроводе резко перекрыть краном или задвижкой, то возмущение от остановки течения будет распространяться вверх по трубопроводу со скоростью звука, причем уменьшение скорости среды позади такой волны возмущения будет сопровождаться заметным повышением давления. В случае жидкости повышение давления при внезапном перекрытии трубопровода может быть очень большим, и пики давления при взаимодействии прямой и обратной волн представляют собой опасный эффект, называемый гидравлическим ударом. Явление распространения звука в воде, как и в воздухе, имеет и свои полезные стороны - на этом основаны гидролокация и аппаратура для обнаружения подлодок. Во-вторых, сжимаемость приходится учитывать и по той причине, что именно этим свойством определяется возможность анализа жидкости и газа на основе одних и тех же принципов. Критерием при этом служит отношение скорости течения к скорости упругой волны, т.е. к скорости звука в данной среде:
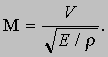
Этот критерий называется числом Маха. (Отметим, что число Маха аналогично числу Фруда, так как последнее есть отношение скорости течения к скорости гравитационной волны.) До тех пор пока величина М мала (Ј 0,5), влияние сжимаемости незначительно. Когда же число Маха приближается к единице, картина течения существенно изменяется в связи со звуковыми эффектами. Например, коэффициент лобового сопротивления снаряда со сферической головной частью зависит только от числа Рейнольдса, пока число Маха не превысит 0,5; после этого он постепенно возрастает и приблизительно удваивается, когда число Маха становится больше единицы, вследствие образования звуковых волн (скачков уплотнения) в зоне сжатия непосредственно перед снарядом (рис. 7). Подобно тому как носовой части быстроходных судов придают заостренную и тщательно спрофилированную форму для уменьшения носовой волны и, следовательно, волнового сопротивления, заостряют высокоскоростные снаряды и носовые части и передние кромки крыльев самолетов, чтобы уменьшить потери в скачках уплотнения, а тем самым уменьшить сопротивление, связанное со звуковыми эффектами. О больших энергетических потерях, обусловленных образованием звуковых волн, можно судить по тому шуму, который создают воздушные винты самолетов, и по пронзительному звуку, которым сопровождается полет снарядов и ракет.
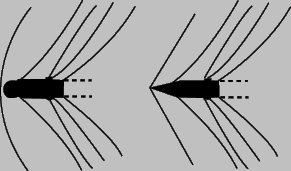
Рис. 7. КАРТИНА ЗВУКОВЫХ ВОЛН, создаваемых снарядами с тупой и заостренной головными частями.
Аналогии между течением жидкости и газа. Тесная аналогия между процессами образования волн "маховского" и "фрудовского" типов дает возможность исследователям, работающим в обоих этих направлениях, собирать ценные плоды, выращенные на общей почве гидроаэромеханики. Так, анализ картины звуковых волн, примененный к картине гравитационных волн в сбросных противопаводковых каналах, позволил существенно усовершенствовать планировку таких каналов. И наоборот, исследования высокоскоростных моделей в сверхзвуковых аэродинамических трубах обычно дополняются исследованиями в буксировочных опытных бассейнах и гидродинамических лотках, где картину волн, создаваемых такими телами, можно изучать визуально. Наряду с такой аналогией между течением жидкостей и газов имеется и различие, которое, однако, тоже служит полезной цели как основа для сравнения. Когда скорость газа в какой-либо точке достигает скорости звука, в этой точке, как уже говорилось, может возникнуть звуковая волна. Скорость жидкости из-за практических ограничений вряд ли когда-либо сможет приблизиться к скорости звука, но в жидкости существует предел, налагаемый давлением насыщенного пара самой жидкости, для понижения давления, связанного с увеличением скорости. Когда скорость жидкости сильно возрастает в какой-либо ее точке, вследствие соответствующего снижения давления жидкость в этой точке вскипает. Это явление называется кавитацией. Быстрое образование тотчас же при повышении давления схлопывающихся пузырьков пара приводит не только к снижению коэффициента полезного действия насосов и гребных винтов, но и к их механическому повреждению и разрушению, если такой процесс продолжается достаточно долго. Аналогия же с течением газа кроется здесь в том, что зоны, опасные для обтекаемого тела, одинаковы как при образовании звуковых волн в воздухе, так и при возникновении кавитации в воде. Но кавитацию легко наблюдать по помутнению прозрачной воды (появлению в ней пузырьков), тогда как для наблюдения звуковых волн необходимо специальное оптическое оборудование. Поэтому модели, для которых существенны звуковые эффекты в воздухе, часто испытывают на кавитацию в гидродинамических трубах, что позволяет усовершенствовать конструкцию и устранить многие опасные зоны.
См. также
ЛИТЕРАТУРА
Седов Л.И. Механика сплошной среды. М., 1976 Страхович К.И. Гидро- и газодинамика. М., 1980 Аэрогидромеханика. М., 1984 Лойцянский Л.Г. Механика жидкости и газа. М., 1987
Орфографический словарь
Морфемно-орфографический словарь
Сканворды для слова гидроаэромеханика
Полезные сервисы
гидроаэроплан
Слитно. Раздельно. Через дефис
Синонимы к слову гидроаэроплан
Большой словарь иностранных слов
гидроаэроплан
- гидросамолёт [см. гидро…] - самолёт, снабжённый приспособлением для посадки на воду и взлёта с воды
Словарь галлицизмов русского языка
ГИДРОАЭРОПЛАН а, м. hydroaéroplane m. Гидросамолет. Вейгелин 1925 Сл. авиа. Здесь, между прочим, имел место чрезвычайно интересный, почти первый в истории военного искусства, бой отряда русских гидроаэропланов с гигантом. Втор. отеч. война 128. Летал гидроаэроплан, разбрасывал прокламации Деникина. 1919. Бунин Лишь слову 124. Гидроаэропланы летали нерегулярно, и только если не ожидалось встречи с англичанами. Иванова Восп. 263. Вчера здесь была большая встреча гидроплана. Весь город устремился вниз по Смоленскому спуску к шести часам. День выдался идеальный. хотя с маленьким ветром. Гидроплан опоздал на 45 минут, летел из Казани. О. А. Толстая-Воейкова (1887-1936 ) Письма 1927 года. // Континент 2003 116 305.