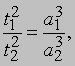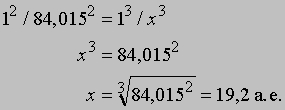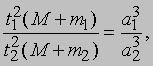Ке́плера зако́ны - три закона движения планет относительно Солнца, установлены как обобщение наблюдательных данных И. Кеплером в начале XVII в. 1-й : каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце. 2-й закон Кеплера: каждая планета движется в плоскости, проходящей через центр Солнца, причём площадь сектора орбиты, описанная радиусом-вектором планеты, изменяется пропорционально времени. 3-й закон Кеплера: квадраты времён обращения планеты вокруг Солнца относятся как кубы их средний расстояний от Солнца. Законы Кеплера были объяснены и уточнены на основе закона тяготения Ньютона.
* * *
КЕПЛЕРА ЗАКОНЫ - КЕ́ПЛЕРА ЗАКО́НЫ, три закона движения планет относительно Солнца, установлены как обобщение наблюдательных данных И. Кеплером (см. КЕПЛЕР Иоганн) в начале 17 в. 1-й Кеплера закон: каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце. 2-й Кеплера закон: каждая планета движется в плоскости, проходящей через центр Солнца, причем площадь сектора орбиты, описанная радиусом-вектором планеты, изменяется пропорционально времени. 3-й Кеплера закон: квадраты времен обращения планеты вокруг Солнца относятся как кубы их средних расстояний от Солнца. Кеплера законы были объяснены и уточнены на основе закона тяготения Ньютона.
КЕПЛЕРА ЗАКОНЫ - принципы движения планет, сформулированные в начале 17 в. И. Кеплером (1571-1630) на основе многолетних наблюдений Т. Браге (1546-1601). Они используются в небесной механике и формулируются так: 1. Орбита любой планеты есть эллипс, в одном из фокусов которого находится Солнце. 2. Планета движется так, что ее радиус-вектор за равные интервалы времени заметает равные площади. (Закон площадей.) 3. Квадраты периодов любых двух планет соотносятся как кубы их средних расстояний от Солнца. (Гармонический закон.) Замечательно, что законы Кеплера, составляющие базис небесной механики, выведены из наблюдений Тихо, выполненных без телескопа.
Закон 1. Тихо поставил перед Кеплером задачу создания научной теории движения Марса. Следуя методике тех лет, Кеплер перепробовал множество комбинаций эпициклов и эксцентриков, но не смог найти подходящую для точного предвычисления наблюдаемого положения планеты. Наконец, он предположил, что орбита Марса эллиптическая, и увидел, что эта кривая хорошо описывает наблюдения, если Солнце поместить в один из фокусов эллипса. Затем Кеплер предположил (хотя и не мог точно доказать этого), что все планеты движутся по эллипсам, в фокусе которых находится Солнце. А орбиту Луны он описал эллипсом, в фокусе которого расположена Земля. Действительно, орбиты всех больших планет - эллипсы, причем у Венеры орбита наиболее округлая (эксцентриситет е = 0,0068), а у Плутона наиболее вытянута (е = 0,2485). Орбиты малых планет - астероидов - тоже эллипсы; наиболее круглая орбита у астероида 1177 Гоннезия (е = 0,0063), а наиболее эксцентричная у 944 Идальго (е = 0,656).
Закон 2. Законы Кеплера полностью эмпирические, они выведены из наблюдений. Чтобы получить закон площадей, Кеплер трудился около восьми лет, проделав громадный объем вычислений. Чем ближе планета к Солнцу, тем быстрее она движется по орбите. Каждый год в начале января Земля, проходя через перигелий, движется быстрее; поэтому видимое перемещение Солнца по эклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленно, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу.
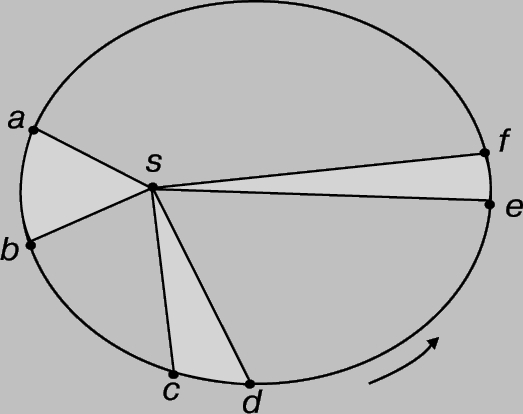
КЕПЛЕРОВСКИЙ ЗАКОН ПЛОЩАДЕЙ. Согласно этому закону, если заштрихованные площади равны друг другу, то планета в своем орбитальном движении вокруг Солнца (S) проходит отрезки ab, cd и ef за одинаковое время.
Закон 3. Третий, или гармонический, закон Кеплера связывает среднее расстояние планеты от Солнца (a) с ее орбитальным периодом (t):
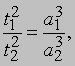
где индексы 1 и 2 соответствуют любым двум планетам. Пример: найти среднее расстояние от Солнца планеты Уран, имеющей период 84,015 лет. Из приведенной выше формулы, взяв период Земли за 1 год и ее расстояние от Солнца за 1 а.е.,
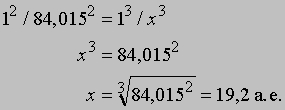
Ньютон (1643-1727) установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до нее, а не от других свойств, таких, как состав или температура. Он показал также, что закон Кеплера не совсем точен; что в действительности в него входит и масса планеты:
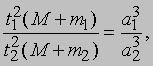
где M - масса Солнца, а m1 и m2 - массы планет. Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их расстояния и орбитальные периоды.