Геометрия - раздел математики, тесно связанный с понятием пространства; в зависимости от форм описания этого понятия возникают различные виды геометрии. Предполагается, что читатель, приступая к чтению этой статьи, обладает некоторыми представлениями об элементарной геометрии, а также о законах арифметики и алгебры.
См. также
Первый важный вопрос: как описать наше понятие пространства? В поисках ответа перед нами открывается несколько возможностей, но проще, а возможно, естественнее и полезнее воспользоваться для этого понятиями "точка" и "прямая". Оба они коренятся в процессе визуального восприятия. Точку можно мысленно представлять как "точку зрения", из которой ведется наблюдение, а прямую, определяемую двумя объектами, считать состоящей из множества точек зрения, при наблюдении из которых один объект заслоняет другой. При таком подходе вводится понятие "прямизны", которое воплощается в термине "прямая линия" (или просто "прямая"). Можно считать, что мы абстрагировали понятия "точка" и "прямая" из окружающего мира. В нашем повседневном опыте коренится еще одно представление - о расстоянии АВ между точками А и В. (Мы говорим также о "длине" отрезка АВ.) О расстоянии мы судим, сравнивая его с некоторым эталоном. Одна из возможных единиц длины - метр; изготовив копии с эталона метра, мы сравниваем расстояния и говорим, что расстояние АВ больше (>), равно (=) или меньше (
(эллиптический параболоид)
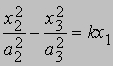
(гиперболический параболоид). Некоторые из этих поверхностей являются "линейчатыми". Это означает, что через каждую точку такой поверхности можно провести по крайней мере две прямые, целиком лежащие на этой поверхности; в результате получим два семейства прямых, любое из которых образует всю поверхность. Эти прямые называют образующими. Если мы ограничимся рассмотрением какой-нибудь одной плоскости, например, положив для этого в уравнении квадратичной поверхности x3 = 0, то получим уравнения конических сечений - кривых, по которым эти поверхности пересекают плоскость x3 = 0. Это - эллипс (частным случаем которого является окружность), гипербола и парабола
(см. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ; КОНИЧЕСКИЕ СЕЧЕНИЯ). Исследование геометрических мест точек, заданных уравнениями, порядок которых больше двух, значительно сложнее. В 1704 И.Ньютон (1643-1727) классифицировал кубические кривые, и с тех пор кривые и поверхности третьего и четвертого порядков стали предметом интенсивного изучения. Хотя методы Декарта существенно упростили идеи греческой геометрии, они же породили много новых трудностей. Некоторые из этих трудностей были преодолены с помощью средств, которыми располагал математический анализ 19 в. Справиться с другими удалось лишь позднее, когда была создана т. н. алгебраическая геометрия (см. АЛГЕБРАИЧЕСКАЯ ГЕОМЕТРИЯ). Интересно отметить, что аналитическая геометрия Ферма и Декарта появилась как раз в то время, когда И. Кеплер (1571-1630), исходя из многочисленных астрономических наблюдений, сделал вывод о том, что планеты движутся по эллипсам, в одном из фокусов которых расположено Солнце. Это подготовило почву для открытия Ньютоном закона всемирного тяготения. Природа даже тогда, когда речь шла о местоположениях далеких планет, соответствовала описанию человеком его представлений о пространстве! Нужно ли удивляться, что для Ньютона "абсолютное пространство по самой своей сущности, безотносительно к чему бы то ни было внешнему, остается всегда одинаковым и неподвижным". Для великого современника Ньютона Г. фон Лейбница (1646-1716) пространство было совокупностью всех возможных отношений расстояния. В следующем разделе мы будем понимать слово "пространство" в более ограниченном смысле.
Проективная геометрия. Наступление 17 в. ознаменовалось настоящим взрывом научной активности. В развитии математики началась новая эра; наряду с Декартом Ж. Дезарг (1593-1662) и Б. Паскаль (1623-1662) попытались по-новому и критически взглянуть на старую евклидову геометрию, чтобы понять, все ли ее результаты представимы в терминах одних лишь точек и прямых. К возникшей в результате такого критического пересмотра проективной геометрии можно подойти, вводя новую систему аксиом, но гораздо поучительнее рассмотреть наши предыдущие исходные допущения и попытаться понять, как их надлежит изменить. Если следовать зрительным восприятиям, то первое, что сразу подпадает под подозрение, - это постулат о параллельных прямых. Нам кажется, что такие прямые все-таки пересекаются в бесконечности. Предположим, что это действительно так, и дополним евклидову плоскость одной "идеальной точкой" или "бесконечно удаленной точкой", общей для любого множества параллельных прямых. Тогда утверждение о том, что прямые l и m параллельны, перейдет в утверждение о том, что прямые l и m пересекаются в бесконечности. Необходимо доказать, что все такие идеальные точки ведут себя так, как если бы они принадлежали "идеальной прямой", которая обладает всеми свойствами, которыми по предположению обладают обычные прямые. Доказательство этого утверждения основывается на знаменитой теореме Дезарга: если соответствующие вершины двух треугольников можно соединить тремя прямыми, пересекающимися в одной точке, то соответствующие стороны пересекаются в точках, лежащих на одной прямой, и обратно. Обосновав присоединение идеальных элементов к евклидовой плоскости, мы можем теперь сказать, что любые две прямые имеют точку пересечения, и в этом заключается основное отличие проективной геометрии. Аналогичным образом мы можем присоединить к трехмерному евклидову пространству "бесконечно удаленную плоскость" и построить проективное пространство любой размерности. Заметим, что теперь мы можем полностью отказаться от понятия "расстояние". Нужно подчеркнуть, что проективная геометрия не есть что-то абстрактное, практически не связанное с внешним миром. Рассмотрим произвольную точку Р и любую плоскость p, не проходящую через точку Р, в обычной евклидовой геометрии. Любая плоскость p1, проходящая через Р, пересекается с плоскостью p по некоторой прямой l1; в частности, плоскость pҐ , проходящая через точку Р и параллельная плоскости p, пересекается с p по прямой lҐ , бесконечно удаленной прямой, лежащей в плоскости p. Таким образом, существует взаимно однозначное соответствие между плоскостями, проходящими через точку Р, и прямыми, лежащими в плоскости p. Если воспользоваться интерпретацией точка = прямая, проходящая через Р, прямая = плоскость, проходящая через Р, то можно проверить, что все аксиомы проективной геометрии выполняются, а потому "пучок" прямых и плоскостей, проходящих через точку Р, образует проективную геометрию плоскости. Вклад Паскаля в геометрию заключается в том, что он показал проективную природу известных со времен Аполлония свойств конических сечений, которые позднее были переведены Декартом на алгебраический язык. Эта работа была завершена Ф. де Лаиром (1640-1718), и, хотя дальнейшее развитие проективной геометрии прервалось и затем продолжилось лишь в 19 в., начало критическому анализу понятия длины было положено.
Непрерывность. Понятие касательной к кривой восходит по крайней мере к Архимеду, но только после того, как Ферма и Ньютон осознали его значение для дифференциального исчисления, это понятие обрело удобную для приложений явную форму. Однако прошло немало лет, прежде чем О.Коши (1789-1857) придал строгость огромному числу теорем, разложениям в степенные ряды, решениям дифференциальных уравнений и т.п., что позволило математическому анализу занять в математике место, сравнимое с геометрией. Понятие числа точек на прямой ничему не соответствует в нашем опыте визуального восприятия пространства, и именно это привело Зенона Элейского к упомянутым выше комментариям. Есть два способа интерпретации понятия непрерывности в терминах интуитивных представлений об окружающем нас мире: 1) через скрупулезный анализ отношений между точками и прямыми и 2) в терминах движения, т.е. средствами математического анализа (см. МАТЕМАТИЧЕСКИЙ АНАЛИЗ).
Конечная геометрия. Хотя целые числа возникают не обязательно в связи с точками прямой, тем не менее естественно рассматривать их как числа, представляющие кратные некоторого единичного отрезка. Это позволяет придать рациональным числам геометрическую интерпретацию, известную еще древним грекам. Однако такой подход к числу недостаточно тонок и сталкивается с трудностями, на которые и указал Зенон; наша концепция пространства включает в себя понятие числа, но для определения чисел понятие пространства не подходит. Возвращаясь к аксиомам проективной геометрии
(см. ПРОЕКТИВНАЯ ГЕОМЕТРИЯ),
заметим, что они не содержат понятия длины и не имеют следствием бесконечность числа точек на прямой. То, что число точек на прямой может быть конечным, подтверждается следующим примером. Предположим, что под точками мы понимаем 15 символов (ab), (ac), (ad), (ae), (af), (bc), (bd), (be), (bf), (cd), (ce), (cf), (de), (df), (ef), где (ij) = (ji). Существуют 35 прямых, каждая из которых содержит три и только три из этих точек. Такие прямые можно разбить на два типа: 1) прямая типа I содержит три точки вида (аb), (bc), (ca); таких прямых 20; 2) прямая типа II содержит три точки вида (ab), (cd), (ef); таких прямых 15. Любая тройка точек, не принадлежащих ни к одному из этих двух типов, определяет некоторую плоскость; существуют 15 плоскостей, каждая из которых содержит семь точек и семь прямых. На прилагаемом рис. 5 показаны расположения точек и прямых на одной из этих плоскостей. (Заметим, что окружность представляет в конечной геометрии прямую.) Нетрудно проверить, что все аксиомы проективной геометрии выполняются, из чего мы заключаем, что они непротиворечивы, но такая геометрия не очень соответствует нашему представлению о пространстве. Чтобы перебросить мост между привычным понятием пространства и построенной нами геометрией, необходимо исследовать возможную связь между точками на прямой и числами арифметики.
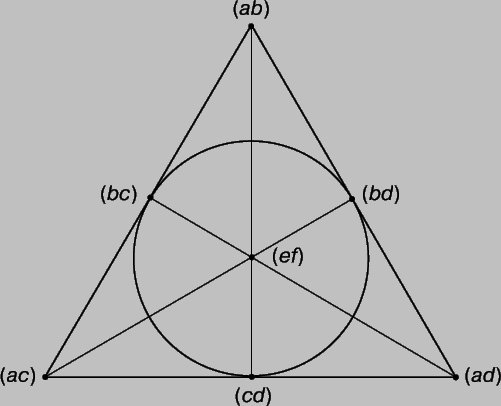
Рис. 5. ПЛОСКОСТЬ ОПРЕДЕЛЯЕТСЯ любыми тремя точками, не лежащими на одной прямой. Например, (ab), (ef), (bc) определяют одну плоскость.
Первым, кто предложил средства, позволяющие геометрически определять операции сложения и умножения, был немецкий математик К.Штаудт (1798-1867), но именно Д. Гильберт (1862-1943) продемонстрировал, что законы арифметики в их геометрической интерпретации зависят от двух теорем - Дезарга и Паппа. В случае конечной геометрии из теоремы Дезарга следует теорема Паппа, а потому если она верна, то верна и теорема Паппа. В этом случае и сложение, и умножение ассоциативны, коммутативны и дистрибутивны, и координаты, которые можно поставить в соответствие точкам на прямой, могут образовать конечное "поле". Если число точек на прямой бесконечно (например, если точки на прямой, за исключением бесконечно удаленной точки, могут быть поставлены во взаимно однозначное соответствие с рациональными числами), то "сложение" точек на прямой ассоциативно и коммутативно при условии, что выполняется теорема Дезарга. Если размерность n > 2, то это заведомо так. Однако из семи аксиом проективной геометрии теорема Паппа не следует; это означает, что умножение, будучи ассоциативным, необязательно коммутативно. При n = 2 теорема Дезарга может не выполняться, и "алгебра" точек на прямой еще более усложняется. Возможные недезарговы плоскости исследуются с 1902, но многое еще остается неизвестным. Если потребовать, чтобы для каждого действительного числа нашлась соответствующая ему точка на прямой, то мы получим т.н. "непрерывную" геометрию. Это требование выполняется введением дополнительного предположения, которое в свою очередь можно использовать для доказательства теоремы Паппа. Такая аксиома непрерывности описывает тот аспект нашего понятия пространства, который был Лейбницем охарактеризован как "лабиринт континуума". Тем не менее роль алгебры в геометрии стала очевидна, и в дальнейшем обе эти ветви математики стали нерасторжимы.
Дифференциальная геометрия. Определив касательную к плоской кривой в точке (y1, y2) с помощью "углового коэффициента" m = dy2/dy1, мы можем записать ее уравнение в виде
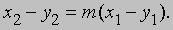
Записанное с помощью дифференциалов, это уравнение принимает вид
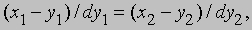
и его непосредственное обобщение приводит к уравнениям касательной к неплоской кривой в точке (y1, y2, y3):
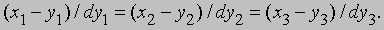
В то время как понятие углового коэффициента не допускает обобщения, понятие направляющего числа легко обобщается, и в качестве направляющих чисел рассматриваемой прямой можно принять дифференциалы. Уравнение соприкасающейся плоскости (плоскости касательных) к неплоской кривой задается определителем
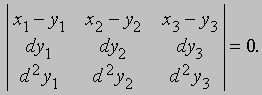
Все эти уравнения имеют явный вид, если рассматриваемое геометрическое место точек задано аналитически, например, параметрически формулами y1 = y1 (t), y2 = y2 (t), y3 = y3 (t). Дифференциальная геометрия стала самостоятельным разделом математики после того, как Б.Риман (1826-1866) заметил, что теорема Пифагора допускает дальнейшее обобщение, и предложил определять меру длины как
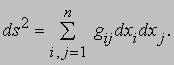
При n = 3 и gij = 1 (если i = j) и gij = 0 (если i № j) мы получаем евклидову геометрию в декартовых (прямоугольных) координатах; другие возможные выборы величин gij приводят к множеству новых геометрических систем, в частности, к геометрии специальной и общей теорий относительности. В конце 19 в. для разработки этих идей был изобретен тензорный анализ, который оказался одним из наиболее подходящих языков для современной физики. Таким образом, методы математического анализа привели нас к идеям, весьма отличным от тех, которые были известны древним грекам. В частности, огромное значение получило понятие "геодезической" - линии, целиком лежащей на поверхности и являющейся кратчайшим путем между двумя точками. Если уравнение некоторой поверхности записать в параметрическом виде: x1 = x1 (u,v), x2 = x2 (u,v), x3 = x3 (u,v), то геометрические места точек u = const, v = const называются "параметрическими кривыми" этой поверхности, а параметры (u,v) задают на этой поверхности "криволинейные координаты". На поверхности Земли мы определяем свое местонахождение, указывая "широту" и "долготу"; из этих двух систем параметрических кривых линии долготы являются большими кругами и, следовательно, геодезическими. В случае декартовой геометрии параметрическими кривыми служат прямые, параллельные осям координат, и все такие прямые - геодезические.
См. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ. Неевклидова геометрия. Смелое допущение Евклида о параллельных прямых, содержавшееся в его знаменитом пятом постулате, почти две тысячи лет было для математиков источником смутного беспокойства, но серьезные попытки доказать его на основе иных допущений были предприняты только в 18 в. И хотя они оказались безуспешными, математикам все же удалось показать, что постулат о параллельных Евклида эквивалентен требованию равенства суммы углов треугольника двум прямым углам, или, что то же, p радианам. Поэтому скорее психологическим, чем математическим прорывом стало осознание существования двух других возможных вариантов: 1) сумма углов треугольника всегда больше p; в этом случае параллельных прямых не существует, и любые две прямые пересекаются; 2) сумма углов треугольника всегда меньше p; в этом случае для любой точки Р, не лежащей на данной прямой l, существуют две прямые l' и l ", проходящие через Р и параллельные данной прямой l, и любая прямая, лежащая внутри угла, заключенного между l' и l ", не пересекается с l. Непротиворечивость второго варианта была осознана К. Гауссом (1777-1855), но впервые опубликована независимо друг от друга Я. Бойяи (1802-1860) и Н.И.Лобачевским (1792-1856) в 30-х годах 19 в. Риман был первым, кто понял, что первый вариант реализуется в сферической геометрии, развитой для нужд астрономии и мореплавания. Было бы ошибкой думать, будто математика на протяжении столетий не претерпела никаких изменений. Постижение тонких идей происходит медленно, и когда мы оглядываемся назад, в прошлое, наши величайшие достижения нередко представляются очень простыми. А. Кэли (1821-1895) и Ф. Клейн (1849-1925) прояснили связь между двумя упомянутыми вариантами, разработав в аналитической форме то, что ими было названо "эллиптической" и "гиперболической" геометриями. Евклидова геометрия является предельным случаем каждой из них, и это верно в отношении любой из аналитических формул таких геометрий. Большие круги (геодезические) на сфере, являющейся поверхностью постоянной положительной кривизны, играют роль прямых и порождают эллиптическую геометрию; аналогичным образом, на поверхности постоянной отрицательной кривизны геодезические порождают гиперболическую геометрию. Можно построить и другие наглядные и поучительные модели эллиптической и гиперболической геометрий, но важно сознавать, что все эти модели содержатся в более общем подходе Римана. Трудно переоценить философское значение этих идей. Человек словно снял темные очки и увидел свое представление о пространстве "при дневном свете", что открыло новые, более интересные и захватывающие возможности, чем он мог себе вообразить. То, что Гаусс предпринял попытку измерить сумму углов треугольника, образованного тремя горными вершинами в Германии, было естественным следствием его понимания того, что постулат Евклида о параллельных явился результатом выбора из ряда возможностей, хотя выбора, несомненно, наилучшего для наших повседневных нужд. И хотя Гауссу не удалось обнаружить никаких отклонений от p, выходящих за пределы допустимой экспериментальной ошибки, это отнюдь не положило конец попыткам предпринять аналогичные крупномасштабные измерения с помощью гигантских телескопов и электронных устройств (см. НЕЕВКЛИДОВА ГЕОМЕТРИЯ). В последние десятилетия наши представления о пространстве сильно изменились под воздействием повсеместного принятия в физике концепции "пространства-времени". Связывание воедино двух фундаментальных понятий вынуждает нас перенести все внимание с "положения" на "событие". Выбирая из многообразия римановых метрик некоторую, в чем-то более предпочтительную, мы может более удовлетворительным образом скоординировать результаты современной физики. См. ОТНОСИТЕЛЬНОСТЬ.
Понятие группы. Расцвет геометрических идей в 19 в. убедительно свидетельствовал о необычайной жизненности математических исследований в целом. Но, возможно, самым важным событием в развитии математического мышления в 19 в. стала постепенная кристаллизация понятия "группы" в алгебре и осознание его значения для геометрии. Древние греки вполне могли бы натолкнуться на эту идею, будь они более настойчивы в поиске внутреннего смысла симметрии. К проблеме симметрии можно подходить двояко. Если геометрическая фигура остается инвариантной относительно вращения или, более общо, относительно какого-нибудь "преобразования", то можно выписать некоторую систему уравнений, выражающих эти преобразования аналитически. Но возможен и другой подход: мы можем представить себе, что геометрическая фигура остается неизменной, а меняется избранный нами способ ее описания относительно системы координат. По существу речь идет о двух возможных способах интерпретации одного и того же преобразования, но иногда одна интерпретация бывает предпочтительнее другой. Если мы имеем в виду все возможные линейные преобразования, которые оставляют фигуру инвариантной, то говорим, что эти преобразования образуют "группу", которую абстрактно можно определить следующим образом. Если обозначить эти преобразования Т1, Т2 и т.д., а совокупность всех таких преобразований - G, то для любых двух преобразований Ti и Tj из G должны выполняться следующие условия: I. TiTj = Tk также принадлежит G; II. Ti (TjTk) = (TiTj)Tk (свойство ассоциативности); III. В G существует некоторое преобразование Т0, называемое тождественным преобразованием или единицей, такое, что TiT0 = T0Ti = Ti; IV. Для каждого Ti из G существует "обратное преобразование" Ti-1, такое, что TiTi-1 = Ti-1Ti = T0. Число g преобразований Т, содержащихся в G, называется "порядком" группы G. Существует 6 симметрий треугольника, они представлены на рис. 6. Нетрудно проверить, что если ограничиться только вращениями, то для тетраэдра g = 12, для куба и октаэдра g = 24, а для икосаэдра и додекаэдра g = 60. Если же кроме вращений допустить отражения и отражения с вращениями, то число g возрастет вдвое. То, что у куба и октаэдра должна быть одна и та же группа вращений, неудивительно, т.к. вершины одного многогранника служат центрами граней другого. Аналогичное утверждение справедливо относительно икосаэдра и додекаэдра. Эти фигура "двойственны" друг другу, тогда как тетраэдр "самодвойствен".
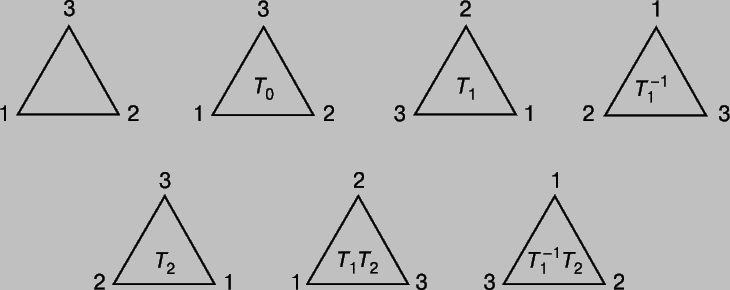
Рис. 6. ШЕСТЬ СИММЕТРИЙ ТРЕУГОЛЬНИКА. Любой из изображенных здесь треугольников может быть получен из первого соответствующим поворотом.
Все преобразования, о которых шла речь, линейны; они переводят точку в точку, прямую - в прямую и плоскость - в плоскость. Такие "коллинеации" имеют особое значение для описания нашего представления о пространстве, основанного на точках и прямых. Клейн первым понял, что множество всех линейных преобразований, оставляющих метрику инвариантной, позволяет адекватно описывать рассматриваемую геометрию, и это привело Клейна к классификации геометрий по их группам коллинеаций. В проективной геометрии метрика отсутствует, поэтому соответствующая ей группа называется "полной линейной группой". В евклидовой геометрии любое вращение оставляет инвариантной сумму квадратов координат, и соответствующая коллинеация называется "ортогональной"; т.к. комбинация двух ортогональных преобразований есть снова ортогональное преобразование, все ортогональные преобразования образуют "ортогональную группу". Параллельные переносы также оставляют метрику инвариантной, поэтому группа "перемещений фигуры как твердого тела" содержит ортогональную группу в качестве своей нормальной подгруппы. Такой подход к изучению геометрии был предложен Клейном в его Эрлангенской программе (1872), которая явилась большим шагом вперед, поскольку предлагала единую точку зрения на ранее существовавшие различные геометрии. Понятие группы получило дальнейшее развитие. До сих пор мы предполагали, что каждое преобразование линейно, но это ограничение несущественно, коль скоро каждое преобразование имеет обратное, которое однозначно определено. Исследование таких "бирациональных" преобразований в общем виде началось с работ Л. Кремоны (1830-1903). В 1870 было доказано, что любое бирациональное преобразование может быть порождено составными квадратичными преобразованиями. Важно подчеркнуть существование некоторых особых точек или геометрических мест, для которых взаимно однозначное соответствие нарушается; именно это обстоятельство порождает специфические проблемы алгебраической геометрии, над решением которых билось немало математиков.
См. также АЛГЕБРА АБСТРАКТНАЯ.
Топология. Общая теория групп преобразований была построена С. Ли (1842-1899), который почти в одиночку возделал огромную территорию математики, оказавшую впоследствии воздействие почти на все ее разделы. Что же касается влияния Ли на геометрию, то оно сказалось прежде всего на расширении самого смысла термина "геометрия", в результате чего граница между геометрией и анализом оказалась размытой. Та часть "ничейной земли", в которой алгебраический характер преобразования предается забвению, получила название "топологии". Топология имеет дело с взаимно однозначными и непрерывными преобразованиями, называемыми "гомеоморфизмами". Изучение топологических пространств позволило открыть множество красивейших теорем. С 1895, когда А.Пуанкаре впервые в явном виде рассмотрел гомеоморфные преобразования топологических пространств, и по сей день топология находится в состоянии интенсивного беспрецедентного развития. Поясним суть ее проблем на одном примере. Возьмем некоторую поверхность и будем ее рассматривать как резиновую пленку, которую можно сжимать и растягивать, но не рвать. Тогда никакие из разрешенных операций не могут преобразовать сферу в тор (бублик); число дыр в поверхности называется ее "родом" и является "топологическим инвариантом". Аналогичный инвариант существует и для односторонних поверхностей, таких как лист Мебиуса (см. также ТОПОЛОГИЯ). Существует масса примеров, когда к топологии обращаются в поисках новых, стимулирующих идей и подходов, чувствуя, что иначе "не пробиться", как, например, в теории контурного интегрирования Коши. Наше представление о пространстве - это наиболее изученная модель, позволяющая лучше всего понять те абстракции, которые и составляют суть математики в целом. Именно такая интерпретация слова "геометрия" позволила уяснить истинное значение этой науки и причину, по которой люди занимаются ее изучением на протяжении вот уже 2500 лет.