ж.
1. Раздел математики, изучающий свойства переменных числовых величин и общих методов решения задач при помощи уравнений.
2. Учебный предмет, содержащий основы данного раздела математики.
3. разг.
Учебник, излагающий содержание данного учебного предмета.
А́ЛГЕБРА, алгебры, мн. нет, жен. (от араб.). Отдел математики, часть математического анализа (см. анализ).
А́ЛГЕБРА, -ы, жен. Раздел математики, изучающий такие качества величин, к-рые вытекают из отношений между величинами и не зависят от их природы.
| прил. алгебраический, -ая, -ое.
АЛГЕБРА - жен. наука счисления буквами и другими условными знаками, взамен цифр, которые вставляются только при окончательном выводе; буквосчисление, общая арифметика. Алгебраический, алгебрический, к сему способу относящийся. Алгебраист, алгебрист муж. сведущий в науке этой.
А́ЛГЕБРА, -ы, ж
Раздел математики, изучающий общие приемы действий над величинами, выраженными буквами, независимо от их числовых значений.
В колледже алгебра изучалась особенно глубоко.
А́ЛГЕБРА -ы; ж. [лат. algebra из араб.].
1. Раздел математики, изучающий общие приёмы действий над величинами (выраженными буквами), независимо от их числовых значений.
2. Учебная дисциплина и урок по изучению этого раздела математики в средней школе. Получить пятёрку по алгебре. Опоздать на алгебру. Прогулять алгебру. Не в ладах с алгеброй кто-л. (о том, кто плохо понимает, не разбирается в этой дисциплине). На алгебре занимались повторением (разг.). // Учебник по этой дисциплине. Листать алгебру.
* * *
а́лгебра (араб.), часть математики, развившаяся в связи с задачей о решении алгебраических уравнений. Решение уравнений 1-й и 2-й степеней известно ещё с древности. В XVI в. итальянскими математиками найдены решения уравнений 3-й и 4-й степеней. К. Гауссом установлено (1799), что всякое алгебраическое уравнение n-й степени имеет n корней (решений), действительных или комплексных. В начале XIX в. Н. Абель и Э. Галуа доказали, что решения уравнений степени выше 4-й, вообще говоря, нельзя выразить через коэффициент уравнения при помощи алгебраических действий. В современной алгебре изучается общая теория совокупностей, в которых определены алгебраические операции, аналогичные по своим свойствам действиям над числами. Такие операции могут выполняться, например, над многочленами, векторами, матрицами и т. д.
* * *
АЛГЕБРА - А́ЛГЕБРА (араб.), часть математики (см. МАТЕМАТИКА), развивающаяся в связи с задачей о решении алгебраических уравнений (см. АЛГЕБРАИЧЕСКОЕ УРАВНЕНИЕ). Решение уравнений 1-й и 2-й степеней известно еще с древности. В 16 в. итальянскими математиками найдены решения уравнений 3-й и 4-й степеней. К. Гауссом (см. ГАУСС Карл Фридрих) установлено (1799), что всякое алгебраическое уравнение n-й степени имеет n корней (решений), действительных или мнимых. В нач. 19 в. Н. Абель (см. АБЕЛЬ Нильс Хенрик) и Э. Галуа (см. ГАЛУА Эварист) доказали, что решения уравнений степени выше 4-й, вообще говоря, нельзя выразить через коэффициент уравнения при помощи алгебраических действий. В современной алгебре изучается общая теория совокупностей, в которых определены алгебраические операции, аналогичные по своим свойствам действиям над числами. Такие операции могут выполняться, напр., над многочленами (см. МНОГОЧЛЕН), векторами (см. ВЕКТОР (в математике)), матрицами (см. МАТРИЦА (в математике)) и т. д.
АЛГЕБРА (араб.) - часть математики, развивающаяся в связи с задачей о решении алгебраических уравнений. Решение уравнений 1-й и 2-й степеней известно еще с древности. В 16 в. итальянскими математиками найдены решения уравнений 3-й и 4-й степеней. К. Гауссом установлено (1799), что всякое алгебраическое уравнение n-й степени имеет n корней (решений), действительных или мнимых. В нач. 19 в. Н. Абель и Э. Галуа доказали, что решения уравнений степени выше 4-й, вообще говоря, нельзя выразить через коэффициент уравнения при помощи алгебраических действий. В современной алгебре изучается общая теория совокупностей, в которых определены алгебраические операции, аналогичные по своим свойствам действиям над числами. Такие операции могут выполняться, напр., над многочленами, векторами, матрицами и т. д.
-ы, ж.
Раздел математики, изучающий общие приемы действий над величинами, независимо от их числовых значений.
[лат. algebra из араб.]
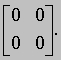
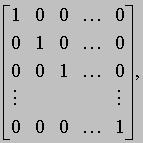
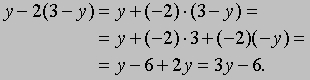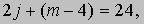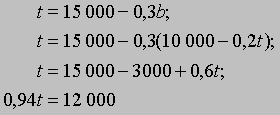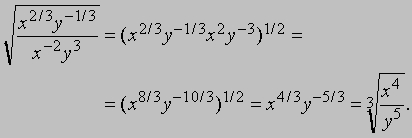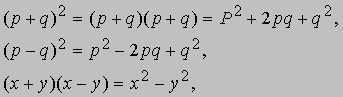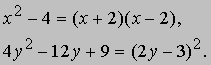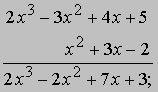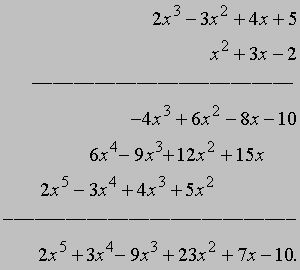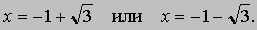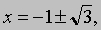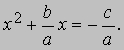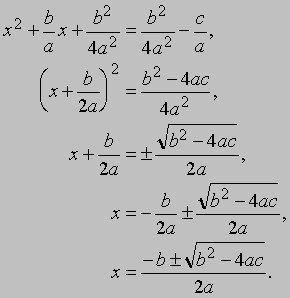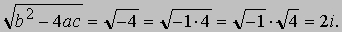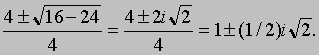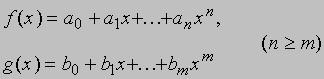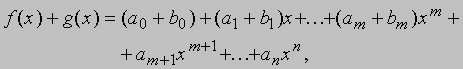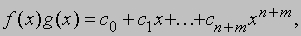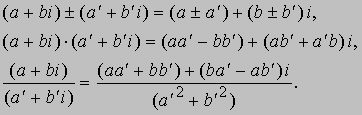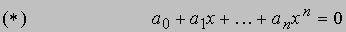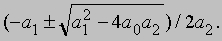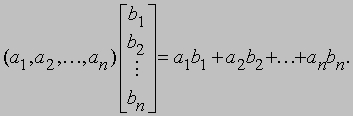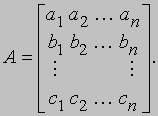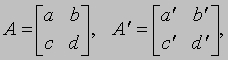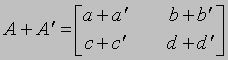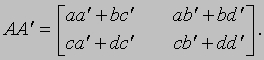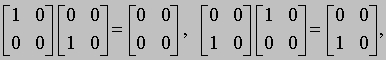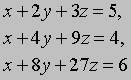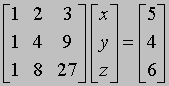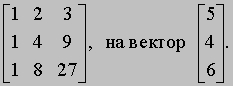АЛГЕБРА - раздел элементарной математики, в котором арифметические операции производятся над числами, значения которых заранее не заданы. Преимущества алгебраических методов обусловлены использованием достаточно компактных символических систем, что внешне выглядит как самая характерная их черта. Термин "алгебра" применяется также для обозначения более абстрактных областей математики, в которых символы используются сходным образом, но необязательно при этом представляют числа
(см. также АЛГЕБРА АБСТРАКТНАЯ; МНОЖЕСТВ ТЕОРИЯ). Для представления чисел можно использовать любые символы, но обычно для этого берут буквы латинского алфавита. Если x и y - два числа, то их сумма обозначается x + y, а разность x - y, т.е. как в арифметике. Так как знак умножения * легко спутать с буквой x, в алгебре знак * используется редко; обычно произведение чисел x и y обозначается xЧy или просто xy. (Знакомые всем позиционные обозначения, используемые при записи целых чисел и означающие, например, что 23 - это не два умножить на три, а два десятка плюс три единицы, в алгебре не применяются.) Аналогично, если одно из встречающихся в задаче чисел указано явно или заранее известно, например число 2, то сумма двойки и любого не указанного заранее числа x алгебраически записывается в виде 2 + x или x + 2, а произведение - как 2x. Множитель 2 в произведении 2x обычно называют коэффициентом. Частные, как правило, записывают в виде дробей; допустима запись x е y, но или (из соображений удобства набора) x/y встречается гораздо чаще. Символ = означает "равно", символ № - "не равно". Например, пусть x - число (если оно существует), такое, что если его удвоить, то оно совпадет с самим собой, увеличенным на три. Чтобы найти x ("неизвестное"), мы можем рассуждать на словах, как это и делали первые алгебраисты до изобретения символических систем, но гораздо эффективнее воспользоваться алгебраическими обозначениями. По условиям задачи, требуется, чтобы 2x = x + 3.
Такое представление равенства двух чисел называется уравнением. Пользуясь известными из арифметики правилами операций над числами, уравнение можно упростить. Если число x удовлетворяет уравнению, то числа 2x и x + 3 равны. Вычитая по x из каждого числа, мы снова получим равные числа, следовательно, можно записать x = 3, и задача решена (см. также АРИФМЕТИКА; ЧИСЛО). Заметим, что вычитание x из обеих частей уравнения приводит к такому же результату, как если бы мы взяли x из правой части уравнения и перенесли его в левую часть с другим знаком, т.е. как -x, в результате чего мы получим уравнение 2x - x = 3,
откуда x = 3. Аналогично, если два числа равны, будут равны также их удвоенные величины и их половины, а в более общем случае будут равны результаты их умножения на одно и то же число. Отсюда следует правило, согласно которому обе части уравнения можно умножать или делить на одно и то же число (кроме нуля). Например, из уравнения 3x = 6 мы заключаем, что x = 2. С другой стороны, если x = 1 и, следовательно, x - 1 = 0, мы не можем делить на x - 1 обе части уравнения x - 1 = 0; если же мы все-таки разделим, то скорее всего получим неверный результат, который можно записать в виде "равенства" 1 = 0.
Символы группировки. Огромные возможности алгебраических символов в полной мере раскрываются лишь когда необходимо записать уравнения более сложные, чем те, которые встречались нам до сих пор. В тех случаях, когда требуется изменить порядок выполнения операций, используются символы группировки членов, главным образом круглые скобки (), квадратные скобки [[]] и фигурные скобки {}. В некоторых случаях порядок выполнения операций несуществен, например, как в выражении 2 + 3 + 4; не важно, прибавим ли мы сначала 2 к 3, а затем прибавим результат, равный 5, к 4, или сначала прибавим 3 к 4, а затем полученную сумму, равную 7, прибавим к 2. Объясняется это тем, что сложение действительных чисел подчиняется закону ассоциативности. С другой стороны, смысл выражения 12 е 2 е 3 совершенно неясен: оно могло бы означать, что 12 следует разделить на 2 (и получить частное, равное 6), а затем полученный результат разделить на 3 и получить 2; или же что 2 следует разделить на 3 и получить частное, равное 2/3, а затем 12 разделить на 2/3 и получить 18. Чтобы исключить столь различные толкования, мы можем записать исходное выражение в виде (12 е 2) е 3 в первом случае и как 12 е (2 е 3) - во втором. Согласно принятому соглашению, операции, указанные в круглых скобках, выполняются первыми. В некоторых случаях смысл выражения определяет принятое соглашение о порядке выполнения операций, без которого выражение допускало бы различные толкования. Например, принято считать, что 2Ч3 + 4 означает 6 + 4, т.е. 10, а не 2*7, т.е. 14. Таким образом, если нет операций, заключенных в скобки, то сначала выполняются последовательно умножение и деление, а затем - сложение и вычитание. Если же мы хотим, чтобы сначала была выполнена операция сложения, то необходимо записать 2*(3 + 4) или просто 2(3 + 4). Используя закон дистрибутивности, это выражение можно упростить: 2(3 + 4) = (2*3) + (2*4). Если встречаются несколько скобок, круглых, прямоугольных и фигурных, то выполнять действия нужно, начиная с внутренних скобок; например, 2{3 + 4[[6 - (2 + 3)]]}
раскрывается последовательно следующим образом: 2{3 + 4[[6 - 5]]} = 2{3 + 4} = 2*7 = 14. К числам, представленным символами, следует применять те же правила, которые определяются свойствами чисел. Например, x + 2(3 - x) = x + 2*3 - 2x = 6 - x;
здесь мы воспользовались законом дистрибутивности, а затем законами ассоциативности и коммутативности сложения. Аналогично,
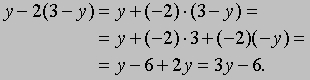
В этом примере мы помимо законов дистрибутивности, коммутативности и ассоциативности, воспользовались правилом, согласно которому произведение положительного и отрицательного чисел отрицательно, а произведение двух отрицательных чисел положительно.
Системы уравнений. В некоторых задачах требуется найти одновременно несколько чисел, для чего необходимо решить несколько уравнений. Предположим, например, что возраст Джона и удвоенный возраст Мэри вместе составляют 32 года, а если бы Джон был вдвое старше, а Мэри на четыре года младше, то им вместе было бы 24 года. Сколько лет Джону и Мэри? Обозначим возрасты Джона и Мэри любыми буквами, например, соответственно j и m. Тогда первое утверждение относительно возрастов можно записать в виде
а второе - в виде
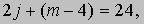
или после упрощения как
Когда два (или больше) числа удовлетворяют двум, как в данном случае, или большему числу уравнений, говорят, что эти числа удовлетворяют системе уравнений. Существуют несколько методов решения систем уравнений. В нашей задаче уравнение (1) (его правую и левую части) можно умножить на 2:
Уравнение (2) утверждает, что 2j + m и 28 - одно и то же число; уравнение (3), если оно верно, останется в силе, если мы вычтем это число из его правой и левой частей, а именно: из левой части мы вычтем 2j + m, а из правой - число 28. В результате мы получим 3m = 36,
откуда m = 12 (т.е. Мэри 12 лет). Используя информацию, содержащуюся в уравнении (1), мы получаем j + 24 = 32 и, следовательно, j = 8 (т.е. Джону 8 лет). Другие методы решения систем уравнений мы продемонстрируем на следующих примерах (каждый из методов пригоден для решения любой из приведенных задач). Предположим, что руководителю предприятия выплачивается 20%-я премия от чистой прибыли, вычисляемой вычитанием из прибыли налогов, но не его премии, и что налоги взимаются в размере 30% от общей прибыли за вычетом причитающейся руководителю премии, но не самих налогов. Предположим, что общая прибыль до вычитания премии и налогов составляет 50 000 долларов. Какова премия и каковы налоги? Задача может показаться неразрешимой, если подходить к ней с позиций арифметики, так как ни премия, ни налоги не могут быть представлены в численном виде, пока мы не узнаем хотя бы одну из этих величин. Однако с помощью алгебраических методов справиться с решением такой задачи не составляет труда. Если обозначить величину премии через b, а размер взимаемых налогов через t, то b = 0,2(50 000 - t), t = 0,3(50 000 - b).
Здесь первое из уравнений утверждает, что b = 10 000 - 0,2t; используя это обстоятельство во втором уравнении, последовательно находим:
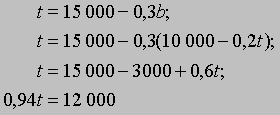
или после округления до ближайших целых чисел (долларов) t = 12 766$, b = 7447$.
Системы линейных уравнений вроде этих можно решать с помощью определителей. В более сложных случаях мы можем воспользоваться различными численными методами их решения. См. также ОПРЕДЕЛИТЕЛЬ. Степени и радикалы. Обозначение x2 (читается "икс в квадрате") используется для сокращенной записи произведения xx (т.е. "икс раз по икс"); например, 32 = 9 и (-1/2)2 = 1/4. Число 2 в этой записи называется показателем степени. Аналогичный смысл имеют более высокие показатели степени: x3 (читается "икс в кубе") означает xxx, а xn (читается "икс в степени n") означает произведение n сомножителей x. Например, 25 = 2*2*2*2*2 = 32. Само число x можно записать как x1 (икс в первой степени), но показатель 1 обычно опускается. Так как 22Ч23 = 25 и вообще xmЧxn = xm+n (в этом нетрудно убедиться, если воспользоваться определением степеней), мы приходим к определениям отрицательных и нулевого показателей степеней: x- n = 1/xn и x0 = 1. Например, 2- 3 = (1/2)3 = 1/8; 20 = 1. (Для нуля отрицательные и нулевая степени не определены.) Равенство xm*xn = xm+n - одно из трех фундаментальных правил действий над степенями, два других правила имеют вид xm*ym = (xy)m и (xm)n = xmn. Например, 23*33 = 63 и (23)4 = 212 = 4096. Повторные показатели следует интерпретировать следующим образом: означает . Таким образом, означает . Это число часто приводят как наибольшее число, которое можно записать с помощью трех цифр. Корнем n-й степени из числа x называется число, n-я степень которого совпадает с x. При n = 2 или n = 3 корни называются соответственно квадратным и кубическим. Например, 3 и -3 - квадратные корни из 9, так как 32 = 9 и (-3)2 = 9; 2 - кубический корень из 8, т.к. 23 = 8; -2 - кубический корень из -8; 1/2 - кубический корень из 1/8. У любого положительного числа существуют два квадратных корня, один положительный и один отрицательный. Положительный квадратный корень из x обозначается , поэтому . (Символ - стилизованная буква латинского алфавита r, первая буква латинского слова "radix" - корень.) Произвольное положительное число имеет n корней n-й степени; если n четно, то оба корня - действительные; если n нечетно, то действительным является один корень. Если x - положительное число, то символ означает положительный корень n-й степени при четном n; если x - положительное или отрицательное число, то означает один из действительных корней n-й степени при нечетном n. Например, , , , , , называются радикалами. Простые радикалы, выражающие иррациональные числа, например , , , и поныне называются несколько устаревшим термином "иррациональности". Следует подчеркнуть, что всегда означает положительный квадратный корень, так что, например, только в том случае, если y - положительное число; если же y отрицательно, то означает положительное число-y . Альтернативные обозначения корней основаны на использовании дробных степеней и предпочтительны с точки зрения удобства типографского набора. Если считать, что дробные показатели степеней должны подчиняться тем же законам, что и целые, то x1/2x1/2 должно означать (x1/2)2 = x1/2Ч2 = x; по определению мы полагаем . Аналогично, x1/n означает корень n-й степени из x, поэтому, например, 81/3 = 2. Естественно, xp/q означает p-ю степень корня q-й степени из числа x или имеет альтернативный (при положительных x - эквивалентный) смысл корня q-й степени из p-й степени числа x. Например, 82/3 = 22 = 4 или 82/3 = 641/3 = 4; 8-2/3 = 1/4 . Определения дробных и отрицательных степеней положительных чисел выбраны так, чтобы при работе с ними сохранялись правила действий с целыми положительными степенями. Например,
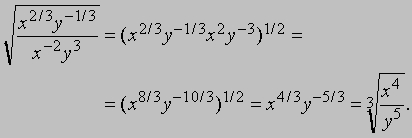
Определить степени отрицательных или комплексных чисел так, чтобы и для них выполнялись все без исключения правила действий над степенями, не представляется возможным. См. также ЛОГАРИФМ.
Тождества. Важную часть алгебры составляют формулы, которые можно использовать для упрощения сложных выражений. Например, справедливо следующее соотношение: (a + b)(c + d) = ac + bc + ad + bd.
Такое равенство называется тождеством; под этим понимается, что независимо от того, какие числа были обозначены символами a, b, c, d, результат выполнения операций, указанных в левой части равенства, совпадает с результатом операций, указанных в правой части равенства. Кстати сказать, приведенное выше тождество используется в арифметике при решении, например, таких задач: 25*36 = (20 + 5)(30 + 6) = 600 + 150 + 120 + 30;
обычная форма записи, принятая при выполнении вычислений, является сокращенной формой этого тождества. Другие тождества, такие как
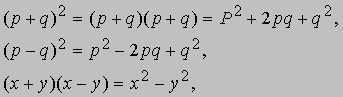
могут использоваться как для упрощения решений в арифметике, так и для строго алгебраических целей. Например, 101*99 = (100 + 1)(100 - 1) = 1002 - 12 = 9999. Первые две из приведенных формул являются частными случаями (с показателем 2) бинома Ньютона (см. также НЬЮТОНА БИНОМ). Эти тождества можно читать и в обратную сторону, т.е. справа налево, для записи алгебраических выражений в виде произведения множителей, например,
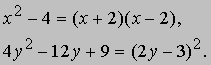
Такая факторизация (разложение на множители) полезна при решении уравнений. Раскрыв произведение (ax + b)(cx + d), мы получим тождество (ax + b)(cx + d) = acx2 + (bc + ad)x + bd.
Довольно часто приходится сталкиваться с задачей представления в виде произведения двух множителей выражений типа x2 - x - 6. Если такое представление с целочисленными коэффициентами возможно, то его можно попытаться найти путем подбора коэффициентов (в рассматриваемом случае x2 - x - 6 = (x - 3)(x +2)).
Многочлены и уравнения. Многочленом называется выражение 2x3 - 5x2 + 6x - 1, в общем виде представляющее собой сумму целочисленных степеней одного и того же числа, взятых с заданными коэффициентами. С помощью десятичной записи целые числа можно представлять в виде многочленов по степеням числа 10, например, 365 = 3*(102) + 6(10) + 5. Если число x в выражении 2x3 - 5x2 + 6x - 1 не задано и может принимать значения из некоторого множества чисел, то оно называется переменной, и формула 2x3 - 5x2 + 6x - 1 определяет некоторую функцию, область определения которой совпадает с тем множеством значений, которые может принимать x. Такая функция называется полиномиальной или для краткости просто полиномом (многочленом); обычно областью определения многочлена принято считать область всех вещественных чисел или множество всех комплексных чисел
(см. ФУНКЦИЯ). Степенью многочлена называют высшую степень входящей в него переменной, например, 2x3 - 5x2 + 6x - 1 - многочлен третьей степени. Любое число, отличное от нуля, рассматриваемое как функция (постоянная, или константа), представляет собой многочлен нулевой степени. Многочлены степеней 1, 2, 3, 4 называются соответственно линейными, квадратными, кубическими и биквадратными. Многочлены можно складывать и умножать так же, как числа, за исключением операции переноса единицы в старший разряд. Последнее вполне естественно, т.к. обычный способ записи чисел по существу является их представлением в виде многочлена по степеням числа 10. Например, чтобы найти сумму многочленов 2x3 - 3x2 + 4x + 5 и x2 + 3x - 2, мы записываем
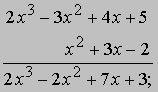
чтобы найти произведение тех же многочленов, мы записываем
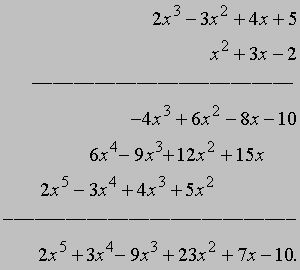
Алгебраическое уравнение (в стандартной форме) - это записанное в алгебраических обозначениях утверждение о том, что некоторая полиномиальная функция обращается в нуль при некотором значении или некоторых значениях переменной (которые требуется найти; например, x2 - 5x + 6 = 0 - алгебраическое уравнение). Уравнение типа 5 - 2x = 6x2 - 3x, приводимое к стандартному алгебраическому уравнению, также называется алгебраическим уравнением. В тех разделах математики, где неалгебраические уравнения (например, ex + 2sin x = 3) не встречаются, вместо слов "алгебраическое уравнение" обычно говорят просто "уравнение". Значения переменной, при которых многочлен обращается в нуль, называются корнями многочлена; они также являются корнями уравнения, получающегося, если многочлен приравнять нулю. Например, многочлен x2 - 5x + 6 имеет корни 2 и 3, т.к. 22 - 5Ч2 + 6 = 0 и 32 - 5Ч3 + 6 = 0; уравнение x2 - 5x + 6 = 0 также имеет корни 2 и 3. Заметим, однако, что в многочлене x2 - 5x + 6 переменная x означает любое число из области определения функции; в уравнении же x2 - 5x + 6 = 0 неизвестная величина x означает одно из чисел, удовлетворяющих уравнению, т.е. превращающих его в тождество, а именно 2 или 3. Линейное уравнение общего вида можно записать как ax + b = 0, где a(№ 0) и b - два заданных числа. Оно имеет решение x = -b/a; таким образом, линейное (степени 1) уравнение имеет ровно один корень. Квадратное уравнение имеет вид ax2 + bx + c = 0. Некоторые простые квадратные уравнения удается решить методом факторизации: если уравнение имеет вид x2 - 5x + 6 = 0,
то его можно также записать в эквивалентной форме (x - 3)(x - 2) = 0,
а последнее выполняется только в том случае, когда x = 3 или x = 2 (т.к. произведение двух чисел равно нулю лишь когда один из сомножителей равен нулю). Следовательно, у интересующего нас уравнения два корня: 2 и 3. Было установлено, что квадратное уравнение обычно имеет два корня, хотя, например, у уравнения x2 - 4x + 4 = 0
только один корень. Считается, что в этом случае оба корня уравнения совпадают, так как многочлен, стоящий в левой части уравнения, можно представить в виде двух линейных сомножителей x2 - 4x + 4 = (x - 2)(x - 2).
Квадратное уравнение типа x2 + 2x + 4 = 0
не имеет действительных корней, т.к. x2 + 2x + 4 = x2 + 2x + 1 + 3 = (x + 1)2 + 3, т.е. значение многочлена x2 + 2x + 4 положительно при любом действительном x; однако у этого уравнения есть, как будет показано ниже, два комплексных корня. Так называемая основная теорема алгебры утверждает, что любой многочлен положительной степени n можно разложить в произведение n линейных сомножителей (возможно, с использованием комплексных чисел), поэтому в общем случае можно сказать, что алгебраическое уравнение степени n имеет n корней (хотя значения некоторых корней могут совпадать). Общий метод решения квадратного уравнения (называемый дополнением до полного квадрата) основан на идее, с помощью которой мы показали, что у уравнения x2 + 2x + 4 = 0 нет действительных корней. В качестве примера мы выберем уравнение, имеющее действительные корни: x2 + 2x - 2 = 0.
Запишем это уравнение в виде x2 + 2x = 2
и прибавим к правой и левой части по 1: x2 + 2x + 1 = 3.
В левой части теперь стоит полный квадрат, поэтому (x + 1)2 = 3.
Это означает, что число x + 1 - один из квадратных корней из 3, т.е.
откуда
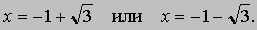
Обычно для краткости это записывают так:
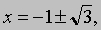
что следует понимать как альтернативу (x принимает либо одно, либо другое значение), но отнюдь не как утверждение о том, будто x принимает два значения одновременно. Следуя той же самой процедуре, мы можем решить квадратное уравнение в общем виде и получить формулу для его корней. Запишем уравнение в виде ax2 + bx + c = 0, где a № 0,
перенесем свободный член в правую часть с противоположным знаком и разделим каждый член уравнения на a:
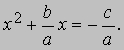
Тогда
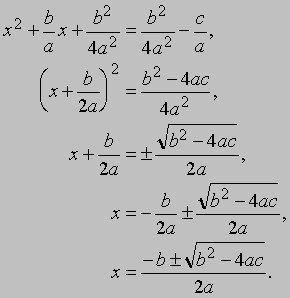
Если величина b2 - 4ac отлична от нуля, то радикал следует понимать как любой из двух квадратных корней из b2 - 4ac, один из которых - положительный, а другой - отрицательный, поэтому полученная формула дает ровно два корня; если величина b2 - 4ac равна нулю, то x = -b/(2a), и мы говорим, что уравнение имеет два равных корня. Если величина b2 - 4ac положительна, то никаких трудностей с извлечением квадратного корня не возникает. Если же величина b2 - 4ac отрицательна, то нам приходится вводить мнимую единицу i, определяемую как квадратный корень из -1, и корни уравнения становятся комплексными. Так, если, например, b2 - 4ac = -4, то
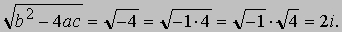
См. также ЧИСЛО. Чтобы продемонстрировать, как действует формула для корней квадратного уравнения в случае, когда b2 - 4ac < 0, рассмотрим уравнение 2x2 - 4x + 3 = 0.
Здесь a = 2, b = -4, c = 3, и корни равны
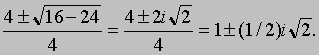
Формула для корней квадратного уравнения остается в силе и в том случае, когда коэффициенты уравнения - комплексные числа, но приводит к необходимости извлекать квадратный корень из комплексного числа, а поэтому менее удобна, чем в случае действительных коэффициентов. Формулы для корней уравнений третьей и четвертой степеней (кубических и биквадратных уравнений) выглядят гораздо сложнее, а для уравнений пятой и более высоких степеней они существуют лишь в отдельных случаях. Когда же коэффициенты уравнения достаточно сложны, например, выражаются числами со многими значащими цифрами, такие формулы не имеют практического значения, и гораздо эффективнее воспользоваться приближенными методами.
См. также УРАВНЕНИЯ. Неравенства. Символы > и < означают соответственно "больше, чем" и "меньше, чем"; например, 2 < 4 и -3 > -5. Неравенства, содержащие неизвестное число, можно решать, пользуясь методами, похожими на те, которыми решают уравнения. Применимы три правила: (i) из обеих частей неравенства можно вычитать одно и то же число, к обеим частям неравенства можно прибавлять одно и то же число; (ii) обе части неравенства можно умножать на одно и то же положительное число (но не на нуль); (iii) при умножении обеих частей неравенства на одно и то же отрицательное число смысл неравенства изменяется на противоположный (т.е. вместо "больше, чем" неравенство переходит в "меньше, чем" и наоборот). В качестве примера решим неравенство -2x - 7 > 2 - 5x.
Пользуясь правилом (i), заменим это неравенство новым: -7 > 2 - 3x,
или -9 > -3x.
По правилу (iii) последнее неравенство эквивалентно неравенству 9 < 3x,
а по правилу (ii) это неравенство, в свою очередь, эквивалентно неравенству 3 < x.
Таким образом, числа x, удовлетворяющие неравенству -2x - 7 > 2 - 5x, это в точности те самые числа, которые больше 3. При умножении на множитель, содержащий неизвестную величину, следует иметь в виду, что этот множитель может быть как отрицательным, так и положительным.
См. также РЯДЫ; ПРОГРЕССИЯ.
ЛИТЕРАТУРА
Курош А.Г. Курс высшей алгебры. М., 1975 Скорняков Л.А. Элементы алгебры. М., 1980
АЛГЕБРА, часть математики, развившаяся в связи с задачей о решении алгебраических уравнений. Слово "алгебра" - арабское (аль-джебр), означает один из приемов преобразования алгебраических уравнений. Решение уравнений 1-й и 2-й степеней известно еще с древности (2-е тысячелетие до нашей эры). В 16 в. итальянскими математиками найдены решения уравнений 3-й и 4-й степеней. К. Гауссом установлено (1799), что всякое алгебраическое уравнение n-й степени имеет n корней (решений), действительных или мнимых. В начале 19 в. Н. Абель и Э. Галуа доказали, что решения уравнений степени выше 4-й, вообще говоря, нельзя выразить через коэффициент уравнения при помощи алгебраических действий. В современной алгебре изучается общая теория совокупностей, в которых определены алгебраические операции, аналогичные по своим свойствам действиям над числами. Такие операции могут выполняться, например, над многочленами, векторами, матрицами и т.д.
Алгебра, ы, ж.
** Алгебра революции.
// Перифрастическое определение философии Гегеля, данное А.И.Герценом в "Былом и думах", чА, гл.25/. Книжн. Высок.
О революционном диалектическом учении.
• Если марксизм в самом деле может быть назван алгеброй революции, то программа, верная духу марксизма, должна быть от начала до конца революционной программой. Плеханов, т. 12, 407. Учение Маркса - современная "алгебра революции". Плеханов, т. 12, 329. + Шанский, Зимин, Филиппов, 14.
Алгебра революции. Книжн., Публ. Революционное диалектическое учение. Перифрастическое определение философии Гегеля. БМС 1998, 22; ШЗФ 2001, 14.
Поверять/ поверить алгеброй гармонию. Книжн. Проверять разумом, точным расчётом то, что выражено чувством. Выражение из трагедии А. С. Пушкина "Моцарт и Сальери". БМС 1998, 22.
а́лгебра, а́лгебры, а́лгебр, а́лгебре, а́лгебрам, а́лгебру, а́лгеброй, а́лгеброю, а́лгебрами, а́лгебрах
↑ относительно, математическая операция
алгебра - наука о математических операциях.
алгебраический.
подстановка. подставить.
дискриминант.
кватернион.
теория матриц: минор. определитель. детерминант. якобиан. транспонирование.
транспозиция.
автоморфизм. эндоморфизм. эпиморфизм.
Это такое привычное и знакомое для нас слово пришло в наш язык издалека - из арабского мира, где в Средние века процветали точные науки. Недаром и те цифры, которыми мы пользуемся, называются арабскими. Al-gabr по-арабски означает "восстановление разрозненных частей" (al - это арабский артикль, наподобие английского "the", немецкого "der" или французского "lа/lе").
Арабское - al-gabr.
Позднелатинское - algebra.
Слово «алгебра» широко известно в русском языке уже с начала XVIII в.
Изначально использовалось в формах: «алгебраика», «алгебрум». Эти формы указывают на прямое заимствование из латинского. В европейских языках слово также восходит к позднелатинскому algebra - «алгебра».
Первоисточник - арабское al-gabr, где al - определительный член, gabr (от глагола gabara) - «вправление», «восстановление», «стеснение».
Обшее значение международного слова «алгебра» - «старейший раздел математики, изучающий свойства и отклонения величин, независимо от их конкретного числового значения».
Производное: алгебраический.
Из польск. яз. в XVIII в. в виде алгебра. Польск. algiebra восходит к нем. Algebra, которое было заимств. из ср.-лат.
Заимств. в XVIII в. из польск. яз., в котором algiebra < нем. Algebra, восходящего к ср.-лат. algebra, переоформлению араб. al gabr «восстановление (разрозненных) частей». Ударение на первом слоге - с конца XVIII в.
Мохаммед бен Муса аль-Хорезми, знаменитый среднеазиатский математик и астроном родом из Хивы, жил в первой половине IX века. Он написал прославленную книгу «Китаб аль-джебр валь-мукабала», посвященную составлению математических уравнений. Через три века, когда она попала в Европу, описанное в книге математическое действие, состоящее в перенесении членов из одной части уравнения в другую с переменой знака, и называвшееся по-арабски аль-джебр, дало название целому разделу математики: аль-джебр - алгебра. (См. также алгоритм).
АЛГЕБРА -ы ж. algèbre f., нем. Algebra <ср.-лат. algebra. 1380. Лексис. мат. Алгебра же назвася от изобретателя гебер нарицаемаго. Арифм. Магн. 226. Имя самое алгебры есть арапское, которые ее назыают Алжабр Валмукабала, то есть наверстать или соравнять. Кантемир Соч. 1867 28. Философии, алжебре, и другим неведомым и бесконечным наукам учиться. ФЭ. Классу была дана задача из алгебры, я, зная, что мой сосед очень плох в алгебре и станет списывать у меня, нарочно написал на доске бессмысленное решение. Быстро списав, он поспешили показать учителю раньше других. Когда же П. И. Исаков взглянул на доску, то конечно, при слове "болван" дал ему славную кокосу, после чего он <сосед> возвратился на свое место, грозя мне мщением. Кокосой назывался удар по голове сложенными крепко тремя пальцами, из коих первенствовал средний. А. П. Беляев Восп. декабриста 46. - Удар. АТ: алге/бра; Нордстет 1780: алге/бра; САР-1 и САР-2: а/лгебра.
АЛГЕБРА (араб. al djebr - восстановление разрозненных частей). Часть математики, рассматривающая общие величины, обозначая их буквами и знаками.
- «Математика уравнений».
- Наука о жизни и удивительных превращениях иксов и игреков.
- Арифметика после «вторжения» в неё латинского алфавита.
- Наука, в которой «с иксами задачи».
- Арифметика, выучившая латинский алфавит.
- Именно ею пушкинский Сальери «проверил гармонию».
- Какой раздел математики изучает кольца и поля? .
- Математика для старшеклассников.
- Напарница начала анализа по учебнику.
- Раздел математики, изучающий уравнения.
- Раздел математики, изучающий свойства величин независимо от их цифрового значения.
- Арабское слово «аль-джебр» - «восстановление» - дало название этому разделу математики.
- Какая наука произошла от сокращения дроби?
- Раздел элементарной математики, в котором арифметические операции производятся над числами, значения которых заранее не заданы.
- Наука о количественных соотношениях и уравнениях.
АЛГЕБРА АБСТРАКТНАЯ (общая алгебра), раздел современной математики, выросший из исследования уравнений и теории чисел. Свою теперешнюю форму абстрактная алгебра начала приобретать лишь в двадцатом веке. Занимается главным образом изучением систем, элементы которых можно сочетать по различным правилам, получая в результате новые элементы, вне зависимости от конкретной природы самих элементов. В последние десятилетия абстрактная алгебра все глубже проникает в различные разделы математики, становясь неоценимым средством исследования в столь различных ее областях, как геометрия, топология, математический анализ и дифференциальные уравнения. Даже у социологов и аналитиков, работающих в сфере бизнеса, возникает необходимость в хотя бы поверхностном знакомстве с теорией матриц, являющейся частью абстрактной алгебры. Фактически в настоящее время сложилась такая ситуация, что наиболее важными являются не те достижения абстрактной алгебры, которые способствуют углублению наших знаний в самой этой области, а те, что предлагают новые средства исследования для других ветвей математики. Абстрактная алгебра оказалась полезной не только в математике. Ее средства и методы используются всюду, где возникает потребность в организации больших объемов данных. Абстрактная алгебра нашла применение при решении широкого круга проблем - от проектирования электронных схем до составления суточных графиков работы нефтеперегонных заводов, позволяющих максимизировать прибыль. Кратко остановимся на некоторых основных алгебраических системах.
Группы. Группой G называется множество, или набор, элементов a, b, ... (относительно их природы не делается никаких предположений), в котором задана операция, ставящая в соответствие каждой паре элементов a, b из G третий элемент, ab, называемый их произведением, причем (i) (ab) c = a (bc), т.е. произведение элемента ab и еще одного элемента c из G равно произведению элементов a и bc; (ii) для любой пары элементов a, b из G существуют элементы x и y из G, такие, что xa = b, ay = b. (Такая операция обычно называется умножением.) Следует заметить, что условие (ii) означает возможность деления в группе. Действительно, в силу условий (i) и (ii) в G всегда существует такой элемент 1 (называемый единицей или единичным элементом), что 1a = a1 = a для всех элементов a группы G, и для каждого элемента a из G в G существует элемент 1/a, называемый его обратным, такой, что a (1/a) = (1/a) a = 1. Тогда мы можем записать x = b (1/a), y = (1/a) b. Различать элементы x и y необходимо, поскольку не предполагалось, что ab = ba. Следует ясно сознавать, что слова "умножение" и "деление" используются в теории групп просто для операции, ставящей в соответствие двум элементам a и b исходного множества третий элемент той же группы, для которого с тем же успехом можно было бы использовать символы a * b, a + b или a Щ b. Таким образом, для того чтобы задать конкретную группу, нужно указать множество ее элементов, определить на нем операцию умножения и, наконец, проверить, что введенное умножение удовлетворяет условиям (i) и (ii). Приведем несколько примеров групп. (A) Множество всех положительных и отрицательных целых чисел, включая нуль, ..., -3, -2, -1, 0, 1, 2, 3, ..., где в качестве произведения двух чисел берется их обычная сумма. Условие (i) - просто закон ассоциативности сложения a + (b + c) = (a + b) + c; что касается условия (ii), то можно положить x = y = b - a.
(B) Множество всех отличных от нуля рациональных чисел (дробей p/q, где p и q - положительные или отрицательные целые числа) с произведением, определенным, как обычно: (p/q)(p'/q') = pp'/qq'. Условие (i), как и в предыдущем примере, - это одно из основных свойств чисел, а условие (ii) удовлетворяется, если для a = p/q, b = p'/q' положить x = y = b : a = p'q/q'p. (C) Более абстрактным примером может служить так называемая циклическая группа порядка n: множество ее элементов составляют n символов a0, a1, a2, ..., an - 1, а произведение определяется соотношением akal = ar, где r = k + l, если k + l < n; если же k + l і n, то r - остаток от деления числа k + l на n. Условия (i) и (ii) проверяются без труда, a0 играет роль единичного элемента, а 1/ak = an - k. В этих трех примерах умножение коммутативно, т.е. ab = ba. Группы с таким умножением называются коммутативными или абелевыми в честь Н. Абеля (1802-1829). (D) Пусть H - множество всех вращений плоскости вокруг некоторой неподвижной точки P, а также ее отражений относительно заданной прямой l, проходящей через P. Если a и b - два элемента из H, то под ab условимся понимать преобразование плоскости, получаемое при выполнении сначала преобразования b, а затем преобразования a. Взяв все возможные произведения элементов из H, мы получим группу G, называемую двумерной ортогональной группой. Слово "ортогональная" в названии группы указывает на то, что преобразования из G сохраняют прямые углы. Нетрудно видеть, что условие (i) выполняется; что же касается условия (ii), то если определить 1/a для любого элемента a из G как преобразование, которое уничтожает действие преобразования a, то x = (1/a) b, y = b (1/a) будут удовлетворять условию (ii). Эта группа неабелева. Действительно, пусть a - поворот на 45° вокруг точки P, а b - отражение относительно заданной прямой. Рассматривая, что произойдет с произвольно выбранной точкой, не лежащей на этой прямой, нетрудно убедиться, что ab № ba. (E) Наш последний пример - так называемая симметрическая группа, Sn, n-й степени. Это множество всех подстановок на n символах 1, 2, 3, ..., n. В данном случае подстановка - это замена каждого целого числа i от 1 до n другим числом, f(i), также заключенным между 1 и n, причем так, что f(i) № f(j), если i № j. Под fЧg здесь понимается подстановка, которая получается при выполнении сначала подстановки g, а затем подстановки f. Условия (i) и (ii) проверяются так же, как мы проверяли их в примере (D). При n > 2 группа Sn неабелева. Например, в S3, если f и g заданы соотношениями f (1) = 2, f (2) = 3, f(3) = 1, g(1) = 3, g(2) = 2, g(3) = 1, то (fg)(1) = f(g(1)) = f(3) = 1, но (gf) (1) = g(2) = 2; поэтому fg № gf. Одна из основных задач теории групп - более явное описание структуры некоторых классов групп. Как показывают приведенные примеры, существует огромное количество самых разных типов групп: группы бывают конечные ((C) и (E)) и бесконечные ((A), (B) и (D)), абелевы и неабелевы, и можно указать еще множество других типов, отличающихся во многих важных отношениях. Таким образом, нужно доказывать утверждения типа: "если группа G удовлетворяет некоторым предположениям, она должна выглядеть таким-то и таким-то образом". Примером таких утверждений является следующая теорема: любая абелева группа, состоящая из конечного числа n элементов, где n - простое число, является циклической группой порядка n. Теория групп находит применение почти во всех разделах математики, играя роль связующего звена между многими, на первый взгляд совсем разными, ее областями. Пример групп (D) показывает, что эта теория очень полезна при рассмотрении геометрических задач, но она оказывает неоценимую помощь и в чисто аналитических разделах математики. Все шире используют теорию групп в своей работе и физики-теоретики. Чтобы еще раз продемонстрировать, как используется теория групп в геометрии, отметим, что различные геометрии (евклидова, гиперболическая, эллиптическая и т.д.) на плоскости можно охарактеризовать их группами движений. Иначе говоря, эти группы различаются своей структурой, и все геометрические факты допускают переформулировку в виде чисто теоретико-групповых теорем. Группы имеют также очень важное значение в топологии - разделе геометрии, изучающем общие соотношения формы и пространства, не обращая внимания на метрические характеристики размера. Например, топологическая задача о том, сколькими способами одна резиновая сфера может быть обернута вокруг другой, сводится к вычислению некоторых групп - так называемых гомотопических групп.
Кольца. Множество R элементов a, b, c, ... называется кольцом, если каждой паре элементов a, b из R поставлен в соответствие некоторый элемент из R, называемый их суммой и обозначаемый a + b, и еще один элемент из R, называемый их произведением и обозначаемый ab. Кроме того, должны выполняться следующие условия: (1) a + (b + c) = (a + b) + c;
(2) a + b = b + a;
(3) для любых двух элементов a, b из R существует элемент x из R, такой, что a + x = b; (4) (ab) c = a (bc); (5) a (b + c) = ab + ac, (b + c) a = ba + ca. Внимательный читатель заметит, что выполнение условий (1), (2) и (3) означает, что R - абелева группа по сложению. Единственный элемент x, такой, что a + x = a (существование которого может быть доказано), называется нулевым элементом кольца R и обозначается 0. Исходя из свойств (1)-(5), нетрудно доказать, что для каждого элемента a из кольца R справедливо равенство aЧ0 = 0Чa = 0. Однако есть кольца, в которых нулем может оказаться произведение ненулевых элементов, т.е. в таких кольцах существуют элементы a, b, ни один из которых не равен 0, но для которых ab = 0. Такие кольца называются кольцами с делителями нуля. (Мы встретимся с ними в разделах, посвященных полям и матрицам.) Многие тождества, известные из обычной алгебры, выполняются и в произвольных кольцах: все обычные тождества, содержащие только сложение и вычитание, а также тождества, не использующие коммутативность умножения или возможность деления, сохраняют силу и в произвольном кольце R. Например, тождество a [[(b + c) + (e + f)]] = (ae + ac) + (ab + af) остается верным в любом кольце R. Примерами колец могут служить уже упоминавшееся множество всех целых чисел с обычными операциями сложения и умножения и множество всех многочленов f (x) = a0 + a1x + ... + anxn, где ai - действительные числа, а x - переменная. Два многочлена являются одним и тем же элементом кольца в том и только в том случае, когда коэффициенты при одинаковых степенях переменной x равны. Сумма многочленов
определяется так:
а их произведение - так:
где cj = a0bj + a1bj - 1 + ... + aj - 1b1 + ajb0. Проверка пяти условий из определения кольца - занятие утомительное, но не сопряженное с какими-либо реальными трудностями. Она опирается на тот факт, что эти условия выполняются для действительных чисел. В обоих примерах умножение коммутативно (т.е. ab = ba), и оба эти кольца не содержат делителей нуля. Пример некоммутативного кольца с делителями нуля мы приведем в заключительном разделе. Как и в случае групп, хотелось бы описать кольца более полно. Эта проблема частично решена, и мы вернемся к ней чуть позже. Коммутативные кольца без делителей нуля типа приведенных выше встречаются в различных теоретико-числовых проблемах, и существует хорошо разработанная теория колец этого класса.
Самой знаменитой теоретико-числовой проблемой, немало способствовавшей развитию теории колец, по праву следует считать так называемую великую теорему Ферма: "Если n - натуральное число, большее двух, то не существует таких отличных от нуля целых чисел x, y, z, что xn + yn = zn". (На полях своего экземпляра Арифметики Диофанта П.Ферма сформулировал эту теорему, отметив, что нашел ее "поистине чудесное доказательство", но не привел его.) К настоящему времени эта теорема доказана, но не элементарными методами, которые могли быть доступны Ферма, а с помощью теории эллиптических кривых. Однако значительная часть теории колец возникла в результате попыток доказать теорему Ферма. В частности, эти попытки привели к введению понятия идеала. Подкольцо S кольца R (т.е. некоторое подмножество элементов кольца R, такое, что разность и произведение любых двух элементов из S суть снова элементы из S) называется идеалом кольца R, если для каждого элемента s из S и каждого элемента r из R оба произведения rs и sr принадлежат S. Поскольку подробное изложение теории идеалов увело бы нас далеко в сторону от цели статьи, упомянем лишь, что в коммутативных кольцах некоторые типы идеалов играют такую же роль, как простые числа в кольце целых чисел, и что такие геометрические объекты, как алгебраические кривые на плоскости, могут быть полностью описаны идеалами в кольце многочленов от двух переменных. При проектировании электронных схем очень полезными оказываются кольца R, каждый элемент r которых удовлетворяет соотношению r2 = r. Вычисления в рамках таких "булевых колец" в точности соответствуют некоторым правилам проектирования схем, так что задача построения схемы, удовлетворяющей заданным условиям, сводится к более простой задаче упрощения соответствующего выражения в булевом кольце.
Поля. Полем F называется коммутативное кольцо, в котором ненулевые элементы образуют абелеву группу по умножению. Это означает, что над элементами поля все четыре рациональные операции (сложение, вычитание, умножение и деление на ненулевые элементы) могут проводиться так же, как над обычными числами, и что для полей остаются в силе все правила элементарной алгебры. Приведем несколько примеров полей. Множество всех действительных чисел с обычными операциями сложения, вычитания, умножения и деления. Множество всех комплексных чисел (всех чисел вида a + bi, где a и b - действительные числа и i2 = -1) также дает пример поля. Четыре рациональные операции в этом случае определяются следующим образом:
Нетрудно проверить, что все условия из определения поля при таком задании операций на указанном множестве выполняются. Еще один пример поля - множество всех чисел вида, где a, b - рациональные числа, с операциями сложения, вычитания, умножения и деления, очень похожими на операции, введенные на множестве комплексных чисел в предыдущем примере, с той разницей, что i заменяется на, а равенство i2 = -1 - на равенство . Более удивительный пример поля получается следующим образом. Любое целое число при делении на 3 дает один из остатков 0, 1, 2. Разделим множество всех целых чисел на три класса так, чтобы все числа, принадлежащие к одному классу, давали при делении на 3 один и тот же остаток. Обозначим эти классы через {0}, {1} и {2}. Тогда число 9 попадает в класс {0}, число 185 - в класс {2}, а число 73 - в класс {1}. Определим сложение и умножение двух классов следующим образом: из каждого класса выберем по одному представителю, произведем сложение или умножение представителей и в качестве результата возьмем класс, которому принадлежит соответственно сумма или произведение представителей (можно проверить, что полученный класс не зависит от выбора представителей и что класс {0} играет роль нулевого элемента). Например, {2} + {2} = {1}, {0} + {1} = {1}, {2}Ч{2} = {1} и {1}Ч{2} = {2}. Те же соображения остаются в силе, если вместо числа 3 мы выберем любое целое число m. Однако поле мы получим только в том случае, когда число m простое (т.е. делится только на себя и на 1). Причина этого очевидна: в поле всегда отсутствуют делители нуля, ибо если ab = 0, но при этом a № 0, то 0 = (1/a)(ab) = b, так как в поле всегда существует элемент 1/a, хотя его, разумеется, может не быть в кольце. Таким образом, в любом поле произведение ab может быть равно нулю только в том случае, когда a или b равно нулю. Если m = m1m2, где m1 № m, m2 № m, то {m1} № 0, {m2} № 0, но {m1m2} = 0 (так как m1m2 дает при делении на m остаток 0). Таким образом, мы можем ожидать, что получится поле - и всегда в действительности получаем поле - только в том случае, когда m - простое число
(см. также ЧИСЕЛ ТЕОРИЯ). Последний пример - поле всех рациональных функций одной переменной, т.е. множество всех отношений многочленов (a0 + a1x + ... + anxn) е (b0 + b1x + ... + bmxm) при обычном определении операций сложения и умножения. Это поле имеет очевидную связь с упоминавшимся выше кольцом многочленов и получается из него взятием всех формальных отношений. Разумеется, аналогичным образом из кольца целых чисел получается поле всех рациональных чисел. Для всех коммутативных колец R без делителей нуля ситуация здесь общая. Мы всегда можем построить поле F формальных отношений элементов кольца R, в котором само R будет содержаться как множество всех элементов вида a е 1. В отличие от ситуации с группами и кольцами мы располагаем довольно полным описанием всех возможных полей. Этим описанием мы обязаны, главным образом, Э. Штейницу (1871-1928). Приведенные выше примеры иллюстрируют все возможные типы полей. Разумеется, и в теории полей осталось еще много нерешенных проблем, однако они значительно тоньше, чем простое описание. Поля важную роль играют при исследовании алгебраических уравнений. Пусть
- уравнение относительно x с коэффициентами из некоторого поля F. Может случиться так, что ни один элемент из F при подстановке вместо x не обращает левую часть формулы (*) в нуль. Однако можно доказать, что всегда существует более широкое поле Fў, содержащее F, такое, что один из его элементов обращает левую часть (*) в нуль. Этот элемент называется корнем уравнения (*). Например, пусть F - поле рациональных чисел и x2 - 2 = 0 - уравнение, которое требуется решить. Тогда в F не существует корня этого уравнения, но поле из третьего примера содержит такой корень, а именно число, и содержит поле F как множество всех элементов вида . Возвращаясь к общему случаю, заметим, что всегда можно найти еще более широкое поле FІ, которое содержит все корни уравнения (*) и является наименьшим из полей, обладающих этим свойством. Изучением взаимосвязи между F и FІ занимается теория Галуа, названная так в честь Э.Галуа (1811-1832). Лучше всего эта взаимосвязь выражается в терминах некоторых групп, что может служить ярким примером взаимопроникновения двух разделов алгебры. Галуа построил свою теорию в связи с исследованием следующей задачи. Давно было известно, что корни уравнения (*) первой, второй, третьей и четвертой степеней (т.е. корни уравнений a0 + a1x = 0, a0 + a1x + a2x2 = 0, a0 + a1x + a2x2 + a3x3 = 0, a0 + a1x + a2x2 + a3x3 + a4x4 = 0) могут быть явно выражены через коэффициенты ai; например, для уравнений второй степени корни имеют вид
Естественно, что делались попытки вывести аналогичные формулы для корней уравнений пятой и более высоких степеней. Н.Абелю в 1824 удалось показать, что для общего (т.е. с буквенными коэффициентами) уравнения пятой и более высоких степеней такой формулы не существует, т.е. что общее уравнение степени n і 5 неразрешимо в радикалах. После этого встал вопрос об условиях, которым должны удовлетворять коэффициенты уравнения, чтобы оно было разрешимо в радикалах. Ответ на этот вопрос был найден Галуа. В частности, согласно теории Галуа, неразрешимость в радикалах общего уравнения степени n, n і 5, связана со строением группы Sn (определенной нами ранее). Теория полей сыграла выдающуюся роль в доказательстве неразрешимости трех знаменитых проблем древности: удвоения куба, квадратуры круга и трисекции угла. Наконец, упомянем о том, что для любого поля F всегда существует поле F0, которое содержит все корни всех уравнений вида (*) с коэффициентами из F при всех возможных n. Если F - поле действительных или комплексных чисел, то F0 - поле комплексных чисел (наш второй пример). Эту теорему часто называют основной теоремой алгебры. Она имеет иную, эквивалентную, формулировку: любой многочлен с комплексными коэффициентами имеет корень в поле комплексных чисел. Доказательства этой теоремы давали многие известные математики (включая Эйлера и Лапласа), но К. Гаусс (1777-1855) первым доказал ее совершенно строго, без предварительного предположения о существовании корней многочлена.
Векторы и матрицы. Знакомые всем физические векторы, используемые для представления объектов, характеризуемых величиной и направлением (наглядно их изображают символами со стрелкой), можно рассматривать и на более абстрактном уровне. Такой подход позволяет понять более сложные операции над векторами, распространить векторную алгебру на случай n-мерного пространства и расширить область применения понятия "вектор". Пусть F - поле. Строка (a1, a2, ..., an) или столбец
из n элементов называется n-мерным вектором-строкой или n-мерным вектором-столбцом v. Два n-мерных вектора-строки v, vў равны в том и только в том случае, если равны все их соответствующие элементы. Векторы можно складывать и вычитать по правилу (a1, ..., an) ± (b1, ..., bn) = (a1 ± b1, ..., an ± bn). Нетрудно проверить, что при таких определениях векторы образуют абелеву группу. Важное значение имеет еще одна операция над векторами: если v = (a1, ..., an) - вектор, а a - элемент из F, то по определению av = (aa1, aa2, ..., aan). Векторы допускают и более абстрактное определение, которое, как можно показать, эквивалентно приведенному выше и существенно увеличивает применимость векторов в различных областях науки. Можно определить произведение двух векторов-строк, но гораздо полезнее следующее определение произведения n-мерного вектора-строки на n-мерный вектор-столбец:
Следует заметить, что такое произведение будет уже не вектором, а просто элементом из F. Матрицей A размера nґn называется множество n-мерных векторов-строк, записанных один под другим (или n-мерных векторов-столбцов, записанных рядом). Например,
Две матрицы A и A' равны в том и только в том случае, когда у них равны все элементы, стоящие на одинаковых местах. Сумма двух матриц размера nґn по определению получается сложением соответствующих векторов-строк, а произведение AAў определяется по следующему правилу: в качестве j-го элемента i-й строки берется произведение i-й строки матрицы A на j-й столбец матрицы Aў. Например, при n = 2 и
имеем
и
Нетрудно проверить, что при таких определениях множество матриц размера nґn образует кольцо. Это кольцо некоммутативно и имеет делители нуля, как показывает следующий пример:
так как нулевым элементом кольца матриц 2*2 служит матрица
Кольцо матриц размера n*n с элементами из некоммутативного поля (системы, обладающей всеми свойствами поля за исключением коммутативности умножения и называемой телом) допускает более абстрактное представление. Точнее говоря, справедлива теорема, которая утверждает, что любое кольцо, удовлетворяющее некоторым двум условиям, обязательно должно быть множеством матриц размера nґn над некоторым телом. Эту теорему можно даже несколько усилить и тем самым получить описание более широкого класса колец. Для некоторых матриц A существуют обратные матрицы; это означает, что для матрицы A существует матрица A', такая, что AA' = A'A = I, где I - единичная матрица
которая обладает тем свойством, что для любой матрицы B справедливо соотношение IB = BI = B. Множество всех таких матриц размера nґn образует группу, и это обстоятельство имеет важное значение для изучения более абстрактных групп, поскольку большой их класс допускает матричное представление. Векторы и матрицы находят все более широкое применение и вне математики. Они были изобретены в середине 19 в. в связи с изучением n-мерной геометрии. С тех пор их стали использовать везде, где приходится иметь дело с обработкой больших массивов данных. С использованием матриц решаются многие технические задачи, связанные с расчетом напряжений, деформаций, колебаний. Решение системы линейных уравнений с несколькими переменными по существу является задачей матричного исчисления. Например, систему уравнений
можно записать в виде
и затем, чтобы найти x, y, z, нужно умножить матрицу, обратную матрице
Матрицы используются и при решении систем дифференциальных уравнений, которые возникают в большинстве наук: такую систему можно заменить одним матричным дифференциальным уравнением. Одно из главных применений матриц в общественных науках связано с построением моделей различных ситуаций. Например, экономическую ситуацию в стране часто моделируют с помощью матрицы с примерно 100 строками и столбцами. На основании операций над такой матрицей экономисты создают свои прогнозы. Пример использования матриц в деловом мире - линейное программирование, которое можно использовать при составлении производственных планов, схем распределения сырья и готовой продукции и в других сложных операциях. Не вдаваясь в подробности, можно сказать, что линейная программа состоит из очень большого числа утверждений о взаимосвязях между различными факторами, которые необходимо учесть перед тем, как принять окончательное решение. Эти утверждения сводятся в некоторую матрицу, операции над которой позволяют программисту решить, какая из нескольких имеющихся процедур оптимальна для решения рассматриваемой проблемы. Это позволяет найти процедуру, обеспечивающую максимальную прибыль или максимальную экономию времени.
ЛИТЕРАТУРА
Калужник Л.А. Введение в общую алгебру. М., 1973 Фрид Э. Элементарное введение в абстрактную алгебру. М., 1979 Общая алгебра (под ред. Л.А.Скорнякова), тт. 1-2. М., 1990
А́лгебра ло́гики - система алгебраических методов решения логических задач и совокупность таких задач.
* * *
АЛГЕБРА ЛОГИКИ - А́ЛГЕБРА ЛО́ГИКИ, система алгебраических методов решения логических задач и совокупность таких задач; в узком смысле - табличное, матричное построение логики высказываний, определяющее логические операции над ними.
АЛГЕБРА ЛОГИКИ - система алгебраических методов решения логических задач и совокупность таких задач; в узком смысле - табличное, матричное построение логики высказываний, определяющее логические операции над ними.
Из мемуаров «Былое и думы» (1855) русского мыслителя, издателя и писателя Александра Ивановича Герцена (1812-1870), который говорит так о философии Гегеля (ч. 4, гл. 25): «Философия Гегеля - алгебра революции, она необыкновенно освобождает человека и не оставляет камня на камне от мира христианского, от мира преданий, переживших себя».
Выражение послужило основой для образования определений, построенных по вышеприведенному образцу.
Книжн., Публ. Революционное диалектическое учение. Перифрастическое определение философии Гегеля. БМС 1998, 22; ШЗФ 2001, 14.
алгебраи́ст, алгебраи́сты, алгебраи́ста, алгебраи́стов, алгебраи́сту, алгебраи́стам, алгебраи́стом, алгебраи́стами, алгебраи́сте, алгебраи́стах
АЛГЕБРИСТ и АЛГЕБРАИСТ -а м. algébriste m., нем. Algebraist, англ. algebraist.1580. Лексис. Знающий алгебру; специалист по алгебре. Не требуется однако ж, чтоб Артиллерийские и Инженерные офицеры были великие Алгебраисты; ибо сия наука весьма трудна, и надлежит употреблять многие годы, чтобы получить в знание. ПСЗ 16 98. Есть и здесь ученые, и между ими, может быть, и алгебрист случится. Воронцов Письма-1 100. Давая в разные стороны сей земли комисии разным ученым людям о приискании мне искуснаго алгебриста и калкулатора, не мог доселева иметь еще удачи. 1786. АВ 9 408. - Лекс. Нордстет: алгебраи/ст.
- Специалист в области раздела элементарной математики, в котором арифметические операции производятся над числами, значения которых заранее не заданы.
Алгебраи́ческая геоме́трия - раздел математики, изучающий алгебраические кривые (поверхности) и их многомерные обобщения - алгебраические многообразия.
* * *
АЛГЕБРАИЧЕСКАЯ ГЕОМЕТРИЯ - АЛГЕБРАИ́ЧЕСКАЯ ГЕОМЕ́ТРИЯ, раздел математики, изучающий алгебраические кривые (поверхности) и их многомерные обобщения - алгебраические многообразия.
АЛГЕБРАИЧЕСКАЯ ГЕОМЕТРИЯ - раздел математики, изучающий алгебраические кривые (поверхности) и их многомерные обобщения - алгебраические многообразия.
АЛГЕБРАИЧЕСКАЯ ГЕОМЕТРИЯ - раздел математики, занимающийся изучением геометрических объектов, связанных с алгебраическими уравнениями, и их обобщениями. Простейший из таких объектов - плоская алгебраическая кривая, заданная уравнением f(x, y) = 0, где f(x, y) - многочлен от координат x и y. Например, окружность x2 + y2 - 1 = 0 и кривая x3 + x2 - y2 = 0 - алгебраические кривые, а y - sin x = 0 - трансцендентная кривая (т.е. алгебраической кривой не является). Алгебраическое уравнение с тремя неизвестными определяет алгебраическую поверхность в пространстве. Две алгебраические поверхности пересекаются по алгебраической пространственной кривой. Понятия "алгебраическая кривая" и "алгебраическая поверхность" допускают обобщения в пространствах размерности более трех, где их аналогами служат алгебраические многообразия. Одна из наиболее важных задач алгебраической геометрии - исследование пересечения двух или более алгебраических многообразий. Основной результат в этой области состоит в том, что у двух алгебраических плоских кривых, заданных уравнениями степеней m и n, не может быть более mn общих точек, если только нет общей кривой (принадлежащей им обеим). Например, прямая (уравнение первой степени) и окружность (уравнение второй степени) могут иметь самое большее две общие точки, но могут иметь и только одну общую точку (если прямая касается окружности) или ни одной. Особая точка алгебраической плоской кривой характеризуется тем, что в ней может существовать более одной касательной. Число касательных называется кратностью точки. Например, (0,0) - особая точка кривой x3 + x2 - y2 = 0. Для любой кривой заданной степени существует предел числа и кратности особых точек, и многие свойства кривой определяются характером ее особых точек. Гораздо сложнее обстоит дело в случае поверхностей и других многообразий. Например, на алгебраической поверхности помимо конечного числа изолированных особых точек могут быть несколько особых кривых, т.е. кривых, каждая точка которых - особая. Переход от кривой f (x, y) = 0 к кривой f (x, xy) = 0 характерен для процесса, известного как квадратичное преобразование. Например, уравнение x3 + x2 -y2 = 0 преобразуется в x3 + x2 - x2y2 = 0 или в x + 1 - y2 = 0 после деления всех членов уравнения на x2. В этом случае у преобразованной кривой нет особых точек, и можно показать, что с помощью последовательности квадратичных преобразований особые точки любой алгебраической кривой можно превратить в неособые. Квадратичное преобразование - простейшее в общем классе бирациональных преобразований. Алгебраическая геометрия в значительной мере занимается изучением действия таких преобразований на кривые и другие алгебраические многообразия, в частности, определением свойств, не изменяющихся при таких преобразованиях. В своем современном виде методы алгебраической геометрии применяются во многих областях математики: теории чисел, теории групп, топологии, теории дифференциальных уравнений и функциональном анализе.
ЛИТЕРАТУРА
Шафаревич И.Р. Основы алгебраической геометрии. М., 1972 Хартскорн Р. Алгебраическая геометрия. М., 1981
АЛГЕБРАИЧЕСКАЯ кривая (поверхность) - кривая (поверхность), выражаемая в декартовых координатах алгебраическим уравнением.
Алгебраи́ческая крива́я (пове́рхность) - кривая (поверхность), выражаемая в декартовых координатах алгебраическим уравнением.
* * *
АЛГЕБРАИЧЕСКАЯ КРИВАЯ (ПОВЕРХНОСТЬ) - АЛГЕБРАИ́ЧЕСКАЯ КРИВА́Я (ПОВЕ́РХНОСТЬ), кривая (поверхность), выражаемая в декартовых координатах алгебраическим уравнением.
Алгебраи́ческая фу́нкция - функция, связанная с независимым переменным алгебраическим уравнением.
* * *
АЛГЕБРАИЧЕСКАЯ ФУНКЦИЯ - АЛГЕБРАИ́ЧЕСКАЯ ФУ́НКЦИЯ, функция, связанная с независимым переменным алгебраическим уравнением.
алгебраическая функция - аналитическая функция, удовлетворяющая алгебр. уравнению (матем).
алгебраическое уравнение. | алгебраические кривые.
порядок, класс кривой - максимальное число касательных, которые можно провести
к данной кривой из произвольной точки плоскости, не лежащей на этой кривой.
алгебраическая геометрия.
▼ линейность, коническое сечение
см. аналитическая функция, в соответствии с
Выражение, в котором постоянные и переменные величины соединяются между собой посредством ограниченного числа алгебраических действий.
АЛГЕБРАИ́ЧЕСКИЙ, алгебраическая, алгебраическое. прил. к алгебра. Алгебраическая задача. Алгебраическое решение.
А́ЛГЕБРА, -ы, ж. Раздел математики, изучающий такие качества величин, к-рые вытекают из отношений между величинами и не зависят от их природы.
АЛГЕБРАИ́ЧЕСКИЙ -ая, -ое. Выраженный или записанный посредством знаков, характерных для алгебры (букв, сочетаний букв и цифр и т.п.). А-ое число. А-ие уравнения. А-ое выражение. А-ая функция.
◁ Алгебраи́чески, нареч. Решить задачу а.
алгебраи́ческий, алгебраи́ческая, алгебраи́ческое, алгебраи́ческие, алгебраи́ческого, алгебраи́ческой, алгебраи́ческих, алгебраи́ческому, алгебраи́ческим, алгебраи́ческую, алгебраи́ческою, алгебраи́ческими, алгебраи́ческом, алгебраи́ческ, алгебраи́ческа, алгебраи́ческо, алгебраи́чески
алгебра́ический
- относящийся к алгебре; а-кая геометрия - раздел математики, изучающий алгебраические кривые и поверхности на плоскости и в пространстве; а-кая функция - функция, связанная с независимой переменной величиной алгебраическим уравнением; а-кие кривые и поверхности - кривые и поверхности, определяемые алгебраическими уравнениями; а-кие числа - числа, являющиеся решениями алгебраических уравнений с целочисленными коэффициентами; а-кое выражение - выражение, составленное из букв и цифр, соединенных знаками действий: сложения, вычитания, умножения, деления, возведения в степень и извлечения корня степени ит. п.; а-кое уравнение - уравнение, каждая часть которого является одночленом или многочленом по отношению к неизвестный величинам.
АЛГЕБРИЧЕСКИЙ и АЛГЕБРАИЧЕСКИЙ ая, ое. algébrique adj., англ. algebraic.1585. Лексис. Отн. к алгебре. Легких опытов, затрудненных в учоных книгах без нужды доказательствами и алгебраическими выкладками. Коз. Расс. 217. Означа .. политическую <науку> буквою П, а Алгебрическую буквою А. Николев Тв. 3 293. Здесь речь не об азбуках вымышленных школьными учителями, и сочиненных по алгебраическим или арифметическим правилам. 1757. Кальер 2001 199. - Лекс. Нордстет 1780: алгебраи/ческий; Сл. 18: алгебраи/ческий 1752.
Алгебраи́ческое выраже́ние - выражение, составленное из букв и чисел, соединённых знаками алгебраических действий: сложения, вычитания, умножения, деления, возведения в степень, извлечения корня.
* * *
АЛГЕБРАИЧЕСКОЕ ВЫРАЖЕНИЕ - АЛГЕБРАИ́ЧЕСКОЕ ВЫРАЖЕ́НИЕ, выражение, составленное из букв и чисел, соединенных знаками алгебраических действий: сложения, вычитания, умножения, деления, возведения в степень, извлечения корня.
АЛГЕБРАИЧЕСКОЕ ВЫРАЖЕНИЕ - выражение, составленное из букв и чисел, соединенных знаками алгебраических действий: сложения, вычитания, умножения, деления, возведения в степень, извлечения корня.
Алгебраи́ческое уравне́ние - уравнение, получающееся при приравнивании двух алгебраических выражений. Например, х2 + ху + у2 = х + 1. Алгебраическое уравнение с одним неизвестным x может быть преобразовано к виду
a0 + a1x + … + anxn = 0.
* * *
АЛГЕБРАИЧЕСКОЕ УРАВНЕНИЕ - АЛГЕБРАИ́ЧЕСКОЕ УРАВНЕ́НИЕ, уравнение, получающееся при приравнивании двух алгебраических выражений. Напр., x2 + xy + y2 = x +1. Алгебраическое уравнение с одним неизвестным может быть преобразовано к виду aо + a1x + ... + anxn = 0.
АЛГЕБРАИЧЕСКОЕ уравнение - уравнение, получающееся при приравнивании двух алгебраических выражений. Напр., x2+xy+y2 =x+1. Алгебраическое уравнение с одним неизвестным может быть преобразовано к виду aо + a1x + ... + anxn=0.
АЛГЕБРАИЧЕСКОЕ УРАВНЕНИЕ, уравнение, которое можно преобразовать так, что в левой части будет многочлен от неизвестных, а в правой - нуль. Степень многочлена называется степенью уравнения. Простейшие алгебраические уравнения: линейное уравнение - уравнение 1-й степени с одним неизвестным ax+b=0, имеющее один действительный корень; квадратное уравнение - уравнение 2-й степени ax2+bx+c=0, которое в зависимости от значения коэффициентов может иметь либо два различных, либо два совпадающих действительных корня, либо не иметь действительных корней. Вообще, алгебраическое уравнение степени n не может иметь более n корней.