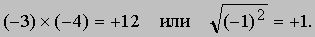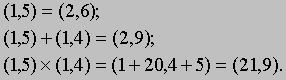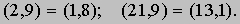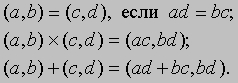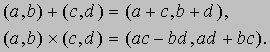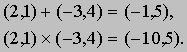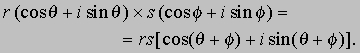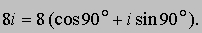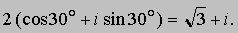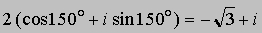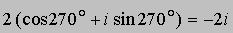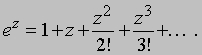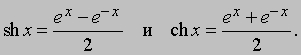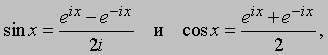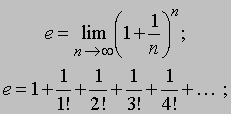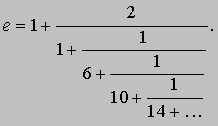Толковый словарь
I ср.
1. Понятие количества.
отт. Величина, при помощи которой ведется счёт; единица счёта.
отт. разг. Цифра, номер.
2. День месяца в порядковом ряду других дней.
отт. разг. Дата.
3. Количество кого-либо или чего-либо, считаемое единицами.
отт. разг. Количество лиц, составляющих какую-либо массу.
4. Совокупность кого-либо или чего-либо.
II ср.
Грамматическая категория имени и глагола, выражающая системами форм - парадигмами - единичность или раздельную множественность предметов, явлений и лиц (в лингвистике).
ЧИСЛО́ - сущ., с., употр. очень часто
Морфология: (нет) чего? числа́, чему? числу́, (вижу) что? число́, чем? число́м, о чём? о числе́; мн. что? чи́сла, (нет) чего? чи́сел, чему? чи́слам, (вижу) что? чи́сла, чем? чи́слами, о чём? о чи́слах
математика
1. Числом называется единичный элемент математических данных.
Дробное, целое, простое число. | Положительные, отрицательные числа. | Число делится на два. | Сумма чисел. | Комбинация чисел. | В десятичной системе это число записывается как 7, в троичной - 21, а в двоичной - 111.
2. Чётное число - это число, которое кратно 2 (делится на 2).
3. Круглые числа - это такие числа, как 10, 20 и т. п., которые в записи оканчиваются цифрой 0.
4. Натуральное число - это число, которое возникает в процессе простого счёта, целое положительное число.
Возьмём произвольное натуральное число: например, 10.
количество
5. Числом называется количество людей, предметов и т. д.
Большое число чего-либо. | Получить равное число голосов. | Семья числом в пять человек. | Число иностранных студентов.
6. Числом называют состав, ряд, группу кого-либо, чего-либо.
Быть в числе первых. | Исключить из числа претендентов. | Принадлежать к числу воздержавшихся. | Попасть в число победителей конкурса. | Войти в число лучших спортсменов.
7. Фраза в том числе (и) означает, что вы включаете кого-то или что-то в какую-то группу лиц или предметов, которая была обозначена ранее.
Пошли все, в том числе и мы.
8. Числом в языкознании называется грамматическая категория, которая выражает единичность или множественность предметов или лиц.
Единственное, множественное число. | Двойственное число в старославянском языке.
9. Если кому-то, обычно ребёнку, попало по первое число, то это означает, что его строго наказали за какую-то провинность, плохой поступок.
За прогуливание уроков в этот день ему попало по первое число.
дата
10. Числом называется день месяца в порядковом ряду других дней.
В первых числах августа. | Какое сегодня число?
11. Если кто-то датирует какой-то документ задним числом, то это означает, что этот человек ставит на нём прошедшую дату, которая не соответствует реальной.
Выписать справку задним числом.
12. Если кто-то что-то делает задним числом, то это означает, что этот человек делает это слишком поздно, несвоевременно.
Толковый словарь Ушакова
ЧИСЛО́, числа, мн. числа, чисел, числам, ср.
1. Понятие, служащее выражением количества, то, при помощи чего производится счет предметов и явлений (мат.). Целое число. Дробное число. Именованное число. Простое число. (см. простой1 в 1 знач.). Теория чисел (отдел математики, изучающий общие свойства чисел).
2. То же, что цифра в 1 знач. (старин.).
3. Тот или иной день месяца в его порядковом ряду, месте (при названии месяца слово "число" в речи обычно опускается, напр. "первое мая" вместо "первое число мая"). Первого числа (т.е. в первый день месяца) он возвращается из отпуска. Какое сегодня число? Какого числа твой день рождения? Пометить письмо задним числом (см. задний), завтрашним, вчерашним числом. «Июня третьего числа коляска легкая в дорогу его по почте понесла.» Пушкин. «В последних числах сентября… в деревне скучно, грязь, ненастье.» Пушкин.
4. только ед., кого-чего. Количество (кого-чего-нибудь, считаемого отдельными особями, единицами, штуками). Собралось большое число гостей. Число книг в библиотеке сильно возросло. Круглым числом (см. круглый в 3 знач.). «Хлопочут набирать учителей полки, числом поболее, ценою подешевле.» Грибоедов.
5. только ед. Совокупность, ряд известного количества кого-чего-нибудь. «А смешивать два эти ремесла есть тьма искусников, я не из их числа.» Грибоедов. В числе присутствующих не оказалось ни одного математика. Все дружно принялись за работу, и новички в том числе.
6. Грамматическая категория, показывающая, об одном или о большем числе предметов идет речь (грам.). Единственное число. Двойственное число (указывает на два предмета). Множественное число (указывает на число предметов больше одного или, в языках, имеющих формы двойственного числа, - на число предметов больше двух). Изменяться в роде, числе и падеже.
• Без числа - в очень большом количестве, в бесчисленном множестве. «У нас же дорога большая была: рабочего звания люди сновали по ней без числа.» Некрасов.
Толковый словарь Ожегова
ЧИСЛО́, -а, мн. числа, -сел, -слам, ср.
1. Основное понятие математики величина, при помощи к-рой производится счёт. Целое ч. Дробное ч. Действительное ч. Комплексное ч. Натуральное ч. (целое положительное число). Простое ч. (натуральное число, не имеющее других делителей, кроме самого себя и единицы). Рациональное ч. Иррациональное ч.
2. День календарного месяца по порядку счёта от начала к концу. В первых числах мая. Какое сегодня ч.? Задним числом пометить или датировать (уже прошедшим, более ранним числом, чем следует). Задним числом сообщить или узнать (позже чем следовало бы; разг.).
3. кого (чего). Количество считаемого, поддающегося счёту. Ч. собравшихся. Значительное ч. ошибок. Отряд числом в двадцать человек (в числе двадцати человек). Большое ч. людей.
4. Состав, ряд, совокупность кого-чего-н. Пополнить ч. участников.
5. В грамматике: категория имени и глагола, специальными системами форм (парадигмами) выражающая единичность или множественность. Единственное ч. Множественное ч.
В числе кого (чего), предл. с род. в составе какого-н. множества, среди кого-чего-н. Быть в числе лучших.
В число кого (чего), предл. с род. в состав какого-н. множества. Попал в число отстающих.
К числу кого (чего), предл. с род. обозначает включённость в состав кого-чего-н. Принадлежать к числу учеников. Проблема относится к числу наиболее сложных.
Из числа кого (чего), предл. с род. из состава какого-н. множества. Назначить бригадира из числа рабочих.
В том числе (-и), союз со знач. присоединения, включения считая, включая. Пошли все, в том числе и мы.
Без числа о неисчислимом множестве. Звёзд на небе без числа.
Числа нет кому (чему) очень много. Поздравлениям нет числа.
По первое число (попадёт, достанется) кому (прост.). о строгом выговоре, наказании. Влетит тебе от отца по первое число.
| прил. числовой, -ая, -ое (к 1 знач.) и численный, -ая, -ое (к 1 знач.; спец.). Числовое программное управление (ЧПУ) (управление механизмами с помощью заранее составленных алгоритмов). Численное решение уравнений.
Толковый словарь Даля
ЧИСЛО - ср. количество, счетом, на вопрос: сколько? и самый знак, выражающий количество, цифра. Без числа; нет числа, без счету, многое множество. Поставь приборы, по числу гостей. Числа римские, арабские или церковные. Целое число, ·противоп. дробь. Четное число, что делится на два без дроби. Круглым числом, средним. Число месяца, день, по счету, счетом, начиная с первого до 31-го. Татарове реша: дайте нам число, ·стар. счет населенью, перепись народа. Не с числа говоришь, вят., пермяц. неверно, ошибочно, неправду. Число в число на тот месяц. Книга Чисел, четвертая из пяти книг Моисеевых: счисленье еврейского народа, станов и колен его, в пустыне. Занятия расписаны по числам (месяца). Все числом да счетом. В том числе, в сем счету, в общем количестве. Числовой вывод, в числах, в цифрах, количественный. Числить что, исчислять, считать, рассчитывать,
| считать в числе чего, полагать в счет. Его числят, он числится в полку. Вычислить путь планеты. Дочислиться до вывода. Зачислить кого на службу. Исчислить нужды свои. Начислить на кого долг. Отчислять часть доходов в запас. Почислить дело решенным. Перечислить кого в другое ведомство. Он причислен к министерству. Прочислил одну статью, пропустил. Расчислить, почем придется на брата. Арифметики счисляют мудреные задачи. Численье, действие по гл. Численные величины, алг. означенные не буквами, а числами. - люди, ·стар. податные, окладные. Численник ·стар. счетчик, переписчик народа русского, от татар. Говори численно, вят. порядком, правильно, законно, верно. Численность, число, счет чего, количество. Численность населенья все растет. Числитель муж. числящий, исчисляющий что.
| Числитель, верхня цифра дроби, означающая, сколько частей взято от целого, разделенного на столько частей, сколько единиц в знаменателе. Числительный, к числителю относящийся; указывающий число чего либо. - имя, грам. слово, означающее счет. Численка жен., тамб., тул. чисменка ниж., пермяц., олон. чисменница костр. в мотке ниток, и в основе ткацкой, зубок; три нитки; десять численок одна пасма; ниж., костр. чисменка четыре нитки или два гнезда; вологод. 20 чисменок, по 3 оборота, одна пасма; местами 40 чисменок пасма, в 120 ниток. Числовед или числослов, арифметик, счетчик. Числословная, числоведная наука, числоведенье, числословие, арифметика, математика, счетная наука.
Популярный словарь
Число
-а́, мн. чи́сла, чи́сел, с.
1) В математике: наименование количества или величины, при помощи которой производится счет.
Целое число.
Дробное число.
Однозначное число.
Двузначное число.
Умножение чисел.
Сложить два числа.
2) День по порядку счета от начала месяца.
Какое сегодня число? Сегодня уже седьмое число.
Газета за вчерашнее число.
В последних числах сентября... в деревне скучно: грязь, ненастье... (Пушкин).
3) Дата.
Поставить число на документе.
Пометить отчет задним числом.
4) (обычно чего) Количество кого-л. или чего-л.
Число пассажиров.
Большое число гостей.
Бессмертья нет. Материя конечна. Число миров исчерпано давно (Волошин).
5) Состав, ряд, совокупность кого-л. или чего-л.
Быть в числе приглашенных.
Войти в число избранных.
6) В грамматике: категория единственности, двойственности, множественности.
Единственное число.
Двойственное число.
Изменение слов по числам.
Родственные слова:
чи́сленник прост., числово́й (числовой масштаб карты), чи́сленный (численный масштаб карты), бесчи́сленный, чи́слить
Этимология:
Восходит к общеславянскому * čislo (← * čit-slo). Корень * čit- тот же, что в считать, читать. В древнерусском и старославянском языках число имело знач. ‘количество’, ‘счисление’, ‘счет’, ‘определение года’, ‘дата’.
Энциклопедический комментарий:
Наряду с математическим издавна существовали и другие обобщения понятия числа. На протяжении веков человеческое сознание стремилось разгадать символику числовых соотношений. Число один свидетельствовало ему о единстве Бога, два - напоминало о двуединой природе Христа, три - о триединстве Бога, четыре - было символом материального мира. Поэтому мир имеет четыре стороны света, он составлен из четырех элементов. Семь воплощало в себе соединение божественного начала с материальным, представленного человеком. Поэтому все, что касается человека, семерично по своей природе: семь смертных грехов и семь противопоставленных им таинств, семь возрастов, семь планет, управляющих его жизнью, семь дней недели, в которые был сотворен мир, семь тысячелетий мировой истории и т. д.
Астрономи́ческие чи́сла - очень большие в числовом отношении величины.
В том числе́ - среди других, в ряду других.
Нет числа́ (кому/чему) - о бесчисленном множестве кого-л. или чего-л.
Словарь существительных
ЧИСЛО́, -а́, мн чи́сла, род. -сел, дат.-слам, ср
Единица счета, выражающая то или иное количество.
Число 13 считается несчастливым числом.
Энциклопедический словарь
ЧИСЛО́ -а́; мн. чи́сла, -сел, -слам; ср.
1. Единица счёта, выражающая то или иное количество. Дробное, целое, простое ч. Чётное, нечётное ч. Считать круглыми числами (приблизительно, считая целыми единицами или десятками). Натуральное ч. (целое положительное количество). Рациональное, иррациональное ч. Положительные числа. Теория чисел (наука о целых числах). Астрономическое ч. (очень большое).
2. День месяца в порядковом ряду других дней. В первых числах августа. Какое сегодня ч.?
3. Количество кого-, чего-л. В небольшом числе городов. Получить равное ч. голосов. Семья числом в пять человек. Большое ч. чего-л.; несть числа чему-л.; без числа что-л. (об очень большом количестве, о бесчисленном множестве чего-л.).
4. Ряд, совокупность, состав кого-, чего-л. Быть в числе первых. Попасть в ч. победителей конкурса. Назначить бригадира из числа рабочих. Включить в ч. лучших спортсменов.
5. Лингв. Грамматическая категория, выражающая морфологическими средствами языка единичность или множественность предметов или лиц. Единственное, множественное ч. Двойственное ч.
◊ По первое число́ задать, получить и т.п. Разг. О строгом наказании. Задним число́м. 1. Более ранним сроком, чем следует. Датировать справку задним числом. -2. Разг. Слишком поздно. Спохватиться задним числом.
◁ В том числе́ (и), в зн. союза. Включая, присоединяя. Пошли все, в том числе и мы. Числово́й, -а́я, -о́е. Ч-ая величина. Ч-ая последовательность. Ч. масштаб карт. Ч-ые данные. Чи́сленный (см.).
* * *
число - I
число́
одно из основных понятий математики; зародилось в глубокой древности и постепенно расширялось и обобщалось. В связи со счётом отдельных предметов возникло понятие о целых положительных (натуральных) числах, а затем идея о безграничности натурального ряда чисел: 1, 2, 3, 4... Задачи измерения длин, площадей и т. п., а также выделение долей именованных величин привели к понятию рационального (дробного) числа. Понятие об отрицательных числах возникло у индейцев в VI-XI вв. Потребность в точном выражении отношений величин (например, отношение диагонали квадрата к его стороне) привела к введению иррациональных чисел, которые выражаются через рациональные числа лишь приближённо; рациональные и иррациональные числа составляют совокупность действительных чисел. Окончательное развитие теория действительных чисел получила лишь во второй половине XIX в. в связи с потребностями математического анализа. В связи с решением квадратных и кубических уравнений в XVI в. были введены комплексные числа.
II
число́
грамматическая категория, указывающая на количество предметов, обозначаемых данным словом или словом, находящимся с данным в отношениях синтаксического согласования. Число единственное, множественное; в некоторых языках - двойственное, тройственное. Выражается обычно формами словоизменения или словообразования.
III
«число́»
система налогообложения в XIII-XV вв. на подвластных монгольскому государству и Золотой Орде территориях (Китай, Средняя Азия, Иран, Северо-Восточная Русь и др.). Основана на переписи (исчислении, «числе») населения. Налоги взимались поголовно, пропорционально имуществу плательщиков.
IV
число́
«е», то же, что неперово число.
Большой энциклопедический словарь
ЧИСЛО - одно из основных понятий математики; зародилось в глубокой древности и постепенно расширялось и обобщалось. В связи со счетом отдельных предметов возникло Понятие о целых положительных (натуральных) числах, а затем идея о безграничности натурального ряда чисел: 1, 2, 3, 4.... Задачи измерения длин, площадей и т. п., а также выделение долей именованных величин привели к понятию рационального (дробного) числа. Понятие об отрицательных числах возникло у индийцев в 6-11 вв. Потребность в точном выражении отношений величин (напр., отношение диагонали квадрата к его стороне) привела к введению иррациональных чисел, которые выражаются через рациональные числа лишь приближенно; рациональные и иррациональные числа составляют совокупность действительных чисел. Окончательное развитие теория действительных чисел получила лишь во 2-й пол. 19 в. в связи с потребностями математического анализа. В связи с решением квадратных и кубических уравнений в 16 в. были введены комплексные числа.
-----------------------------------
ЧИСЛО - грамматическая категория, указывающая на количество предметов, обозначаемых данным словом или словом, находящимся с данным в отношениях синтаксического согласования. Число единственное, множественное; в некоторых языках - двойственное, тройственное. Выражается обычно формами словоизменения или словообразования.
-----------------------------------
"ЧИСЛО" - система налогообложения в 13-15 вв. на подвластных монгольскому государству и Золотой Орде территории (Китай, Ср. Азия, Иран, Северо-Вост. Русь и др.). Основана на переписи (исчислении, "числе") населения. Налоги взимались поголовно, пропорционально имуществу платильщиков.
Академический словарь
-а́, мн. чи́сла, -сел, -слам, ср.
1. Понятие, служащее выражением количества, при помощи которого производится счет.
Простые числа. Целое число. Положительные числа. Теория чисел (наука о целых числах).
2. День месяца в порядковом ряду других дней.
В первых числах августа.
◊
- То было ровно шесть лет тому, весной, тридцать первого марта, - заметьте число, господа, - накануне… - Первого апреля! - закричал юноша в завитках. Достоевский, Ползунков.
- Кто знает, какое сегодня число? Никандров, Седой Каспий.
3. Количество кого-, чего-л.
Эти заводы - числом десять - занимают собой площадь в шестьсот тысяч десятин. Мамин-Сибиряк, Сестры.
У меня есть одна слабость: мне хочется возможно большее число людей приохотить к писательству. Паустовский, Кара-Бугаз.
4. Состав, ряд, совокупность кого-, чего-л.
[Чертокуцкий] служил прежде в одном из кавалерийских полков, был один из числа значительных и видных офицеров. Гоголь, Коляска.
Дом ее принадлежал к числу приятнейших в городе. Тургенев, Дворянское гнездо.
Я был в числе писателей, встречавших Назыма Хикмета на аэродроме. Сельвинский, Я буду говорить о стихах.
5. лингв.
Грамматическая категория, выражающая морфологическими средствами языка единичность или множественность предметов или лиц.
Множественное число. Двойственное число.
◊
нет (несть) числа{ кому-чему}
без числа
об очень большом количестве, о бесчисленном множестве кого-, чего-л.
в том числе
среди других, в ряду других.
Среди отличившихся при овладении городом были дивизии и полки, пришедшие с Кавказа после боев на Тамани, в том числе и полк Воротынцева. Павленко, В ночь под Новый год.
- астрономические числа
- задним числом
- по первое число
Энциклопедия Кольера
Понятие числа в математике может относиться к объектам различной природы: натуральным числам, используемым при счете (положительным целым числам 1, 2, 3 и т.д.), числам, являющимся возможными результатами (идеализированных) измерений (это такие числа, как 2/3, корень из 3, - их называют действительными числами), отрицательным числам, мнимым числам (скажем, к корню из минус 1) и к другим более абстрактным классам чисел, используемым в высших разделах математики (например, к гиперкомплексным и трансфинитным числам). Число необходимо отличать от его символа, или обозначения, которое его представляет. Мы рассмотрим логические отношения между различными классами чисел (см. также ЦИФРЫ И СИСТЕМЫ СЧИСЛЕНИЯ). Элементарная арифметика оперирует с положительными целыми числами и нулем, с дробями, в известной мере с положительными действительными числами, такими как , и иногда с отрицательными действительными числами. Более сложные действия над отрицательными и мнимыми числами обычно принято относить к компетенции алгебры. Правила, осваиваемые при изучении арифметики, применимы без каких-либо ограничений только к положительным действительным числам, поэтому некоторые действия, производимые над более общими классами чисел, часто кажутся загадочными, например
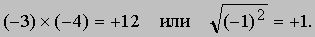
Такие загадки легко разрешаются, если принять во внимание, что различные классы чисел имеют совершенно различный смысл; хотя у них достаточного много общего, чтобы их всех можно было называть числами, не следует думать, что все они будут удовлетворять одним и тем же правилам. Положительные целые числа. Хотя мы все усваиваем положительные целые числа (1, 2, 3 и т.д.) в раннем детстве, когда вряд ли приходит в голову задумываться об определениях, тем не менее такие числа могут быть определены по всем правилам формальной логики. Строгое определение числа 1 заняло бы не один десяток страниц, а формула типа 1 + 1 = 2, если записать ее во всех подробностях без каких-либо сокращений, протянулась бы на несколько километров. Однако любая математическая теория вынуждена начинаться с некоторых неопределяемых понятий и аксиом или постулатов относительно них. Так как положительные целые числа хорошо известны и трудно определить их с помощью чего-то более простого, мы примем их за исходные неопределяемые понятия и будем считать, что основные свойства этих чисел известны.
Отрицательные целые числа и нуль. Отрицательные числа в наши дни вещь обыденная: их используют, например, для того, чтобы представить температуру ниже нуля. Поэтому кажется удивительным, что еще несколько столетий назад какой-либо конкретной интерпретации отрицательных чисел не было, а возникающие по ходу вычислений отрицательные числа назывались "воображаемыми". Несмотря на то, что интуитивная интерпретация отрицательных чисел сама по себе полезна, пытаясь понять такие "правила", как (-4)ґ(-3) = +12, мы должны определить отрицательные числа с помощью положительных. Для этого нам нужно построить множество таких математических объектов, которые будут вести себя в арифметике и алгебре именно так, как можно было бы ожидать от отрицательных чисел. Один из способов построить такое множество состоит в рассмотрении упорядоченных пар положительных чисел (a,b). "Упорядоченность" означает, что, например, пара (2,3) отлична от пары (3,2). Такие упорядоченные пары можно рассматривать как новый класс чисел. Теперь мы должны сказать, когда два таких новых числа равны и что означает их сложение и умножение. Наш выбор определений обусловлен желанием, чтобы пара (a,b) действовала как разность (a - b), которая пока что определена, лишь когда a больше b. Так как в алгебре (a - b) + (c - d) = (a + c) - (b + d), мы приходим к необходимости определить сложение новых чисел как (a,b) + (c,d) = (a + c, b + d); т.к. (a - b)ґ(c - d) = ac + bd - (bc + ad), мы определяем умножение равенством (a,b)ґ(c,d) = (ac + bd, bc + ad); а так как (a - b) = (c - d), если a + d = b + c, мы определяем равенство новых чисел соотношением (a,b) = (c,d), если a + d = b + c. Таким образом,
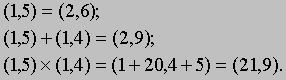
Используя определения равенства пар, можно записать сумму и произведение пар в более простом виде:
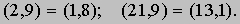
Все пары (a,a) равны (по определению равенства пар) и действуют так, как по нашим ожиданиям должен действовать нуль. Например, (2,3) + (1,1) = (3,4) = (2,3); (2,3)ґ(1,1) = (2 + 3, 2 + 3) = (5,5) = (1,1). Пары (a,a) мы можем обозначить символом 0 (который до сих пор не использовали). Пары (a,b), где b больше a, ведут себя так, как должны были бы действовать отрицательные числа, и мы можем обозначить пару (a,b) символом -(b - a). Например, -4 - это (1,5), а -3 - это (1,4); (-4)ґ(-3) = (21,9), или (13,1). Последнее число хотелось бы обозначить как 12, но это заведомо не то же самое, что положительное целое число 12, поскольку обозначает пару положительных целых чисел, а не одно положительное целое число. Необходимо подчеркнуть, что поскольку пары (a,b), где b меньше a, действуют как положительные целые числа (a - b), мы будем записывать такие числа как (a - b). При этом надо забыть о положительных целых числах, с которых мы начали, и впредь пользоваться только нашими новыми числами, которые назовем целыми числами. То, что мы намереваемся использовать старые названия для некоторых новых чисел, не должно вводить в заблуждение относительно того, что в действительности новые числа представляют собой объекты иного рода.
Дроби. Интуитивно мы представляем себе дробь 2/3 как результат разбиения 1 на три равные части и взятия двух из них. Однако математик стремится как можно меньше полагаться на интуицию и определять рациональные числа через более простые объекты - целые числа. Это можно сделать, если 2/3 рассматривать как упорядоченную пару (2,3) целых чисел. Для завершения определения необходимо сформулировать правила равенства дробей, а также сложения и умножения. Разумеется, эти правила должны быть эквивалентны правилам арифметики и, естественно, отличаться от правил для тех упорядоченных пар, которые мы определили как целые числа. Вот эти правила:
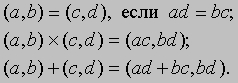
Нетрудно видеть, что пары (a,1) действуют как целые числа a; продолжая рассуждать так же, как в случае отрицательных чисел, мы обозначим через 2 дробь (2,1), или (4,2), или любую другую дробь, равную (2,1). Забудем теперь о целых числах и сохраним их лишь как средство записи определенных дробей.
Рациональные и иррациональные числа. Дроби принято также называть рациональными числами, так как они представимы в виде отношений (от лат. ratio - отношение) двух целых чисел. Но если нам потребуется число, квадрат которого равен 2, то мы не сможем обойтись рациональными числами, т.к. не существует рационального числа, квадрат которого равен 2. То же самое выяснится, если поинтересоваться числом, выражающим отношение длины окружности к ее диаметру. Следовательно, если мы хотим получить квадратные корни из всех положительных чисел, то нам необходимо расширить класс рациональных чисел. Новые числа, называемые иррациональными (т.е. не рациональными), можно определять различными способами. Упорядоченные пары для этого не годятся; один из простейших способов состоит в том, чтобы определить иррациональные числа как бесконечные непериодические десятичные дроби.
Действительные числа. Рациональные и иррациональные числа вместе называются действительными или вещественными числами. Геометрически их можно представить точками на прямой, при этом дроби оказываются в промежутках между целыми числами, а иррациональные числа - в промежутках между дробями, как показано на рис. 1. Можно показать, что система действительных чисел обладает свойством, известным как "полнота" и означающим, что каждой точке на прямой соответствует некоторое действительное число.
Комплксные числа. Так как квадраты положительных и отрицательных действительных чисел положительны, на прямой действительных чисел нет точки, соответствующей числу, квадрат которого был бы равен -1. Но если бы мы попытались решать квадратные уравнения типа x2 + 1 = 0, то необходимо было бы поступать так, как если бы существовало некоторое число i, квадрат которого был бы равен -1. Но поскольку такого числа нет, нам не остается ничего другого, как воспользоваться "воображаемым", или "мнимым", числом. Соответственно, "число" i и его комбинации с обычными числами (типа 2 + 3i) стали называться мнимыми. Современные математики предпочитают называть такие числа "комплксными", поскольку они, как мы увидим, столь же "реальны", как и те, с которыми нам уже доводилось встречаться раньше. Долгое время математики свободно пользовались мнимыми числами и получали полезные результаты, хотя не до конца понимали то, что они делали. И до начала 19 в. никому и в голову не приходило "оживить" мнимые числа с помощью их явного определения. Для этого нужно построить некоторую совокупность математических объектов, которые с точки зрения алгебры вели бы себя как выражения a + bi, если условиться, что i 2 = -1 . Такие объекты можно определить следующим образом. Рассмотрим в качестве наших новых чисел упорядоченные пары действительных чисел, сложение и умножение которых определяется формулами:
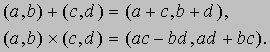
Например,
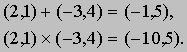
Назовем такие упорядоченные пары комплксными числами. Пары частного вида (a,0) со вторым членом, равным нулю, ведут себя как действительные числа, поэтому мы условимся обозначать их так же: например, 2 означает (2,0). С другой стороны, комплексное число (0,b) по определению умножения обладает свойством (0,b)ґ(0,b) = (0 - b2, 0 + 0) = (-b2,0) = -b2. Например, в случае (0,1)ґ(0,1) мы находим произведение (-1,0); следовательно, (0,1)2 = (-1,0). Мы уже условились записывать комплексное число (-1,0) как -1, поэтому если число (0,1) обозначить символом i, то мы получим комплексное число i, такое, что i 2 = -1. Кроме того, комплексное число (2,3) теперь можно записать в виде 2 + 3i. Важное отличие такого подхода к комплексным числам от традиционного состоит в том, что в данном случае число i не содержит ничего загадочного или мнимого: оно представляет собой нечто, хорошо определяемое посредством уже существовавших ранее чисел, хотя, разумеется, и не совпадает ни с одним из них. Точно так же, действительное число 2 не является комплексным, хотя мы и используем символ 2 для обозначения комплексного числа. Так как на самом деле в мнимых числах нет ничего "мнимого", то неудивительно, что они широко используются в реальных ситуациях, например в электротехнике (где вместо буквы i обычно используют букву j, так как в электротехнике i - символ для текущего значения силы тока). Алгебра комплексных чисел во многом напоминает алгебру действительных чисел, хотя имеются и существенные различия. Например, правило для комплексных чисел не выполняется: , поэтому , в то время как . Определение комплексных чисел как пар действительных чисел подсказывает способ их наглядного геометрического представления. Хотя прямая не может вместить и действительные, и комплексные числа, их вполне может вместить плоскость (см. рис. 2,а). Например, число 2 + 3i представлено точкой плоскости с координатами (2,3) (см. также АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ) .
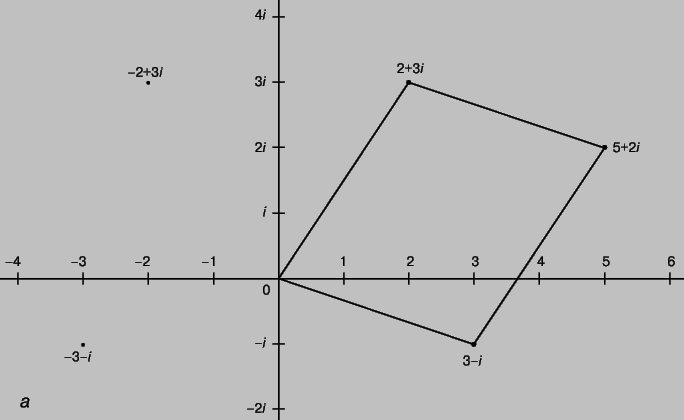
Рис. 2,а. КОМПЛЕКСНЫЕ ЧИСЛА - геометрические представления: a - в декартовых координатах.
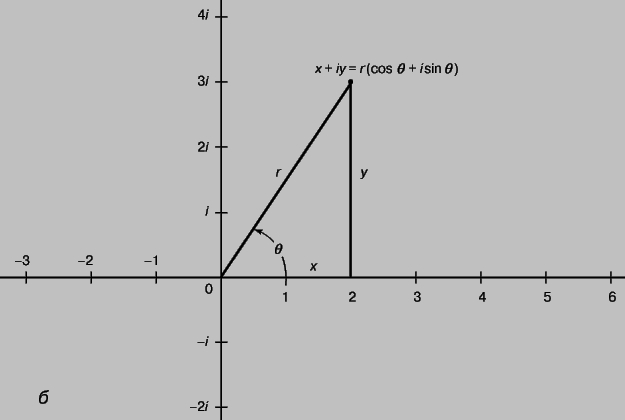
Рис. 2,б. КОМПЛЕКСНЫЕ ЧИСЛА - геометрические представления: б - в полярных координатах.
Сложение комплексных чисел допускает простую геометрическую интерпретацию. Например, сумма чисел 2 + 3i и 3 - i есть число 5 + 2i, которому соответствует четвертая вершина параллелограмма с тремя вершинами в точках 0, 2 + 3i и 3 - i . Точку на плоскости можно задавать не только прямоугольными (декартовыми) координатами (x,y), но и ее полярными координатами (r,q), задающими расстояние от точки до начала координат и угол. Следовательно, комплексное число x + iy может быть записано и в полярных координатах (рис. 2,б). Длина радиуса-вектора r равна расстоянию от начала координат до точки, соответствующей комплексному числу; величина r называется модулем комплексного числа и определяется по формуле . Часто модуль записывают в виде . Угол q называется "углом", "аргументом" или "фазой" комплексного числа. Такое число имеет бесконечно много углов, отличающихся на величину, кратную 360°; например, i имеет угол 90°, 450°, -270°, ј Так как декартовы и полярные координаты одной и той же точки связаны между собой соотношениями x = r cos q, y = r sin q, справедливо равенство x + iy = r (cos q + i sin q). Если z = x + iy, то число x - iy называется комплексно сопряженным с z и обозначается , а в технике z*. Формула z = r2 удобна для вычисления модуля комплексного числа z, особенно если это число определяется сложной формулой. Пользуясь формулами тригонометрии, находим:
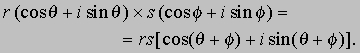
Отсюда правило: чтобы перемножить два комплексных числа, необходимо умножить их модули и сложить их аргументы. В частности, квадрат числа r (cos q + i sin q) равен r 2(cos 2q + i sin 2q), более общая, n-я степень того же числа равна rn(cos nq + i sin nq) (формула Муавра). Эта формула справедлива при надлежащей интерпретации, даже если n - не положительное целое число. Например,
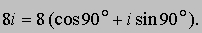
Следовательно, можно ожидать, что кубический корень из 8i (n = 1/3) будет равен
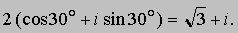
Поскольку аргумент числа i можно считать равным и 90° + 360° = 450°, и 90° + 360° + 360° = 810°, мы можем найти еще два кубических корня из 8i, а именно:
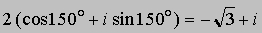
и
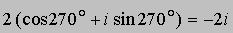
(рис. 3). Любое комплексное число (кроме нуля) также имеет три кубических корня (геометрически расположенных в вершинах равностороннего треугольника) и n корней n-й степени, если n - положительное целое число.
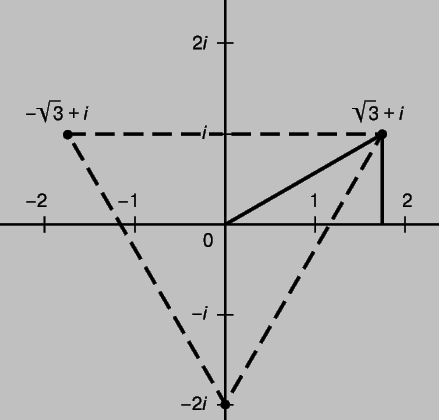
Рис. 3. КУБИЧЕСКИЕ КОРНИ из числа 8i.
Так как мы можем определить целые степени и корни из комплексных чисел, можно ввести и любую рациональную степень, например (2 + i)-3/4. Сложнее определить иррациональные или комплексные степени. Прежде всего необходимо ввести экспоненциальную функцию. Это можно сделать, используя ее разложение в степенной ряд
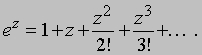
Известно, что если q - действительное число, то eiq определяется этим степенным рядом и eiq = cos q + i sin q; следовательно, тригонометрическая форма комплексного числа представима в компактном виде z = reiq. Логарифм комплексного числа reiq, по определению, равен ln r + iq, где ln означает логарифм по основанию e, а q принимает все возможные значения, измеряемые в радианах. Таким образом, комплексное число имеет бесконечно много логарифмов. Например, ln (-2) = ln 2 + ip + любое целое кратное 2p. В общем виде степени можно теперь определить с помощью соотношения ab = e b ln a. Например, i-2i = e -2 ln i. Так как значения аргумента числа i равны p/2 (90°, выраженное в радианах) плюс целое кратное, то число i -2i имеет значения ep, e3p, e-p и т.д., которые все являются действительными.
Гиперкомплексные числа. Комплексные числа были изобретены, чтобы иметь возможность решать все квадратные уравнения с действительными коэффициентами. Можно показать, что на самом деле комплексные числа позволяют сделать гораздо больше: с их введением становятся разрешимыми алгебраические уравнения любой степени даже с комплексными коэффициентами. Следовательно, если бы нас интересовали только решения алгебраических уравнений, то необходимость во введении новых чисел отпала бы. Однако для других целей необходимы числа, устроенные в чем-то аналогично комплексным, но с большим количеством компонент. Иногда такие числа называют гиперкомплексными. Их примерами могут служить кватернионы и матрицы.
См. также
АЛГЕБРА;
АЛГЕБРА АБСТРАКТНАЯ;
АРИФМЕТИКА;
ФУНКЦИЙ ТЕОРИЯ;
МАТЕМАТИКА;
ЧИСЛО p;
МНОЖЕСТВ ТЕОРИЯ.
Гуманитарный словарь
ЧИСЛО́ (грамматическое) - сопряженные морфол. категории существит., прилаг., местоим. и глагола, образуемые противопоставлением форм ед. и множ. Ч. (стол - столы, синий - синие, он - они, ходил - ходили). Центр. положение среди них занимает категория Ч. существит., обладающая самост. семантич. значимостью и обусловливающая формы Ч. синтаксически связанных с существит.-прилаг., местоим.-прилаг. и глаголов (этот высокий дом - эти высокие дома, дом строится - дома строятся). Исключение составляет употребление глаг. форм в односост. предложениях, когда Ч. глагола, совм. с категорией лица, используется для выражения неопределенно-личности, обобщенно-личности и безличности (К тебе пришли. С ним не соскучишься. Светает). В сочетании с несклон, существит. формы Ч. согласуемых слов являются осн. средством выражения Ч. существит. (висит новое пальто - висят новые пальто).
Формы Ч. существит. служат обычно для различения единичности и неединичности (множественности) называемых предметов или явлений (купил книгу - купил книги, раздался выстрел - раздались выстрелы). Формы ед. Ч. могут также выражать обобщенно-собират. значение (Книга - источник знаний. Рыба здесь не водится), а формы множ. Ч. - обозначать неопред, количество предметов, в т. ч. и равное единице (У нас гости). Отвлеченные, собирательные и веществ. существит., значение к-рых несовместимо с идеей счета, употребляются либо только в форме множ. Ч. (хлопоты, всходы, сливки), либо только или преимущ. в форме ед. Ч. (толщина, листва, молоко). В последнем случае иногда возможно образование форм множ. Ч. при условии сдвига в значении - обозначении конкр. проявлений качества или свойства, разновидностей вещества и др. (наделать глупостей, химические соли). Особое положение занимают существит. типа сутки, ножницы, брюки, не имеющие формы ед. Ч., но способные обозначать и один, и неск. предметов (одни сутки - двое суток).
Среди местоим.-существит. формы Ч. есть только у местоим. 3-го л. (он, она, оно, они). Местоим. я и мы, ты и вы обычно считаются не формами Ч., а самостоят. словами, поскольку мы значит не несколько я, а я и ты (вы) или я и он (они); вы может значить не только несколько ты, но и ты и он (они). Местоим. себя и кто допускают только синтаксич. выражение Ч. в сочетаниях типа самого /самих себя, кто такой / такие. Др. местоим.-существит. требуют согласования в форме ед. Ч. независимо от количества обозначаемых предметов (Что лежит на столе? Книги и тетради).
Формы Ч. образуются с помощью оконч., обычно выражающих одноврем. и др. морфол. значения: у существит. - значение пад. (в доме - в домах), у кратких прилаг., прич., глаголов прош. вр. и сослагат. наклонения - значение рода, а у полных прилаг. и прич. - значение рода и пад., во множ. Ч. род не выражается (ходил, ходила, ходило - ходили; белый, белая, белое - белые), у глаголов изъявит, наклонения - значение лица (читает - читают). Образование форм Ч. существит. может сопровождаться разл. видоизменениями основы (горожанин - горожане, брат - братья, котенок - котята). Встречаются и существит. с супплетивными (разно-корневыми) формами Ч. (человек - люди, ребенок - дети).
Лит.: Реформатский А. А. Число и грамматика // Вопросы грамматики. М., 1960; Исаченко А. В. О грамматическом значении // Вопр. языкознания. 1961. № 1; Соболева П. А. Лексикализация множественного числа и словообразование // Лингвистика и поэтика. М., 1979; Милославский И. Г. Морфологические категории современного русского языка. М., 1981; Булатова Л. И. Еще к вопросу о грамматическом статусе категории числа существительных в русском языке // Проблемы структурной лингвистики, 1981. М., 1983; Поливанова А. К. Выбор числовых форм существительных в русском языке // Там же.
Иллюстрированный энциклопедический словарь
ЧИСЛО, одно из основных понятий математики; зародилось в глубокой древности. В связи со счетом предметов возникло понятие о целых положительных (натуральных) числах: 1, 2, 3,... Задачи измерения длин, площадей и т.п. привели к понятию рационального (дробного) числа. Потребность в точном выражении отношений величин (например, отношение диагонали квадрата к его стороне) привела к введению иррациональных чисел, которые вместе с рациональными числами составляют совокупность действительных чисел. В связи с решением уравнений 1-й степени (линейных уравнений) были введены отрицательные числа, а квадратных уравнений - комплексные числа.
Словарь церковнославянского языка
сущ. (греч. ἀριθμός) - число, цифра. Многое число вещи (τὸ χῦμα τῶν ἀριθμῶν) (2 Мак. 2, 25).
Толковый словарь
Число, а, ср.
**Красное число.
То же, что красный день календаря (См. день).
• И глядит с календаря день седьмого ноября - красное число. Барто, 1988, 227.
Поговорки
Выходить из чисел (из числа). Арх., Кар. Не иметь постоянной календарной даты (о церковных праздниках). АОС 8, 370; МРГК 1, 311.
Без числа. Ряз., Сиб. Выше меры, слишком. ДС, 598; СРНГ 20, 76.
Несть числа кому, чему. Книжн.Устар. О большом количестве кого-л., чего-л. Несть - результат сращения сочетания не есть. БМС 1998, 627; ФСРЯ, 528.
В числах. Сиб. В один и тот же определённый день (о церковных праздниках). Верш. 7, 277.
Всыпать (задать, прописать) по первое число кому. Разг. Сильно наказать кого-л. БМС 1998, 627; БТС, 1480; ФСРЯ, 528; Ф 2, 100; ЗС 1996, 203, 525.
Красное число. Разг. 1. Устар. Праздник, который является нерабочим днем. Мокиенко, Никитина, 1998, 661. 2. Шутл. Начало менструации. Мокиенко, Никитина 2003, 383.
Через число. Волг. Неодобр. Сверх меры (о чём-л. предосудительном, неприемлемом). Глухов 1988, 171.
Задним числом. Разг. Позднее, спустя некоторое время после свершившегося. ФСРЯ, 528; БТС, 320.
Молодым числом. Волог. В молодом возрасте. СВГ 4, 89.
Таким числом. Новг. Тогда. НОС 12, 60.
Ходить одним числом. Смол. В один и тот же день. ССГ 11, 64.
Числом поболее, ценою подешевле. Разг. Ирон. О погоне за количеством в ущерб качеству. Из комедии А. С. Грибоедова «Горе от ума» (1822- 1824 гг.). БМС 1998, 627.
Орфографический словарь
число́, -а́, мн. ч. чи́сла, чи́сел
Словарь ударений
число́, -а́; мн. чи́сла, чи́сел
Трудности произношения и ударения
чи́сло, род. числа́; мн. чи́сла, род. чи́сел и устарелое числ, дат. чи́слам.
Формы слов для слова число
число́, чи́сла, числа́, чи́сел, числу́, чи́слам, число́м, чи́слами, числе́, чи́слах
Синонимы к слову число
сущ., кол-во синонимов: 51
сущ.
количество
численность
Количество, наличность, состав, численность, контингент, сумма, цифра; день..
Ср. . См. день, количество .
небольшое число, несть числа, расти числом...
Тезаурус русской деловой лексики
1.
Syn: количество, численность (кн.)
2.
Syn: дата, день, срок
Идиоматика
астрономическое число
громадное число
максимальное число
наибольшее число
немалое число
подавляющее число
Идеография
▲ знак
↑ выражающий, величина
число - знак, выражающий величину; определенная величина.
числовой. численный.
значение величины.
величина чего.
числовое значение (# функции). количественное значение.
значение переменной - отдельный элемент области изменения;
мгновенная характеристика переменной величины (числовое #).
составлять (# сколько).
объем (# работ. # средств).
цена (# деления шкалы).
числительное.
счетные слова. нумеративы.
именованное число.
отвлеченное число.
балл. очко. разряд.
размерность.
▼ целое число
см. выражать, -ся, некоторое количество
Лингвистика
Число́ -
грамматическая категория, выражающая
количественные характеристики предметов мысли. Грамматическое число -
одно из проявлений более обшей языковой категории количества
(см. Категория языковая) наряду с лексическим проявлением («лексическое число»),
таким, как числительные или как количественные
обозначения в других частях речи (ср. «сотня»,
«единственный», «много», «полно» и т. п.). Как независимая
грамматическая категория число свойственно существительным и личным местоимениям (иногда и местоименным
существительным «кто», «что»), остальные лексико-грамматические
разряды слов имеют синтаксическую категорию
числа: формы числа у них согласуются с формой существительного и
личного местоимения. Не во всех языках такое согласование обязательно; в аналитических языках
(см. Аналитизм) с разрушенной системой
флексий согласование по числу может
быть спорадическим (например, в английском
языке прилагательные и местоимения не
согласуются, ср. my son ‘мой сын’ - my sons ‘мои сыновья’, в глаголе согласование есть только в составных формах
с глаголом be ‘быть’ и в 3‑м лице единственного числа, где аффикс ‑s выражает одновременно лицо и число, ср. I am reading ‘я читаю’ - we are
reading ‘мы читаем’, he sleeps ‘он спит’ -
they sleep ‘они спят’).
Наиболее простая структура категории числа - бинарная
(противопоставление единичности и множественности), она же наиболее
распространена. Но есть системы, содержащие также двойственное
(изредка - тройственное, четверное) число. В существительных такие
формы числа склонны к исчезновению, слиянию с единственным или
множественным числом; например, в древнерусском
языке было двойственное число (дъвѣ руцѣ, род./местный п. дъву руку,
дат./тв. п. дъвѣма рукама), которое оставило следы в украинском диалектном дві руці (‑і
Лингвистические термины
число (грам.)
Класс одноименных морфологических словоизменительных категорий, характеризующих функционирование существительных, местоимений, прилагательных и глаголов. Центральной является категория числа существительных. Число как грамматический признак других частей речи лишь способствует оптимальному проявлению числа существительных. Число существительных - морфологическая словоизменительная категория, представленная формами единственного и множественного числа, выражающими противопоставление по количеству предметов:
а) единичность (ед. ч.);
б) расчлененная (несобирательная) множественность.
Существительные singularia tantum употребляются только в форме ед. ч.:
а) отвлеченные существительные (любовь, сдержанность, преданность и др.);
б) имена собственные (р. Сунжа, Зевс).
Существительные pluralia tantum употребляются только в форме множественного числа;
а) отвлеченные сущ. (хлопоты, переговоры);
б) вещественные (духи);
в) собирательные (финансы);
г) имена собственные (Сокольники);
названия отдельных игр (шахматы).
В профессиональной речи от форм единственного числа могут образовываться формы множественного числа (кислоты, хвои и др.). В разговорной речи наблюдается переносное употребление форм числа: Поднимите, ребята, руку, кто выполнил работу. Число местоимения - морфологическая несловоизменительная категория. Например, числовая корреляция я - мы, ты - вы, он, она, оно - они имеет свои специфические особенности. "Мы" - это не просто множество "Я", но я + он + ты и др. Число глагольных форм и форм прилагательных - это морфологическая словоизменительная категория, служащая целям согласования глаголов и прилагательных с существительными и местоимениями и дублирующая грамматическую информацию, передаваемую главным словом и словосочетанием: он пришел - они пришли. Самостоятельная функциональная значимость глаголов и прилагательных реализуется в сочетании с несклоняемыми существительными: великолепное пальто - великолепные пальто.
Пятиязычный словарь лингвистических терминов
Морфемно-орфографический словарь
Грамматический словарь
Глагольная сочетаемость
возросло число => изменение, субъект, много
выросло число => изменение, субъект, много
иметь октановое число => обладание
ограничивать число => содействие, противодействие
ограничить число => содействие, противодействие
определяться числом => субъект, зависимость, контроль
появилось большое число => существование / создание, субъект, начало
превысить число => много, Neg, оценка, соответствие
превышать число => много, Neg, оценка, соответствие
растёт число => изменение, субъект, много
снизить число => изменение, мало
сократилось число => изменение, субъект, мало
сократить число => изменение, мало
сокращать число => изменение, мало
соответствовать числу => оценка, соответствие
существует большое число => существование / создание, субъект
существует огромное число => существование / создание, субъект
увеличивается число => изменение, субъект, много
увеличивать число => изменение, много
увеличилось число => изменение, субъект, много
увеличить число => изменение, много
уменьшается число => изменение, субъект, мало
уменьшилось число => изменение, субъект, мало
уменьшить число => изменение, мало
умножать число => изменение, много
число возросло => изменение, субъект, много
число составило => оценка, соответствие
число составляет => оценка, соответствие
число увеличивается => изменение, субъект, много
число увеличилось => изменение, субъект, много
Этимологический словарь русского языка
Общесл., сохранившееся не во всех ел. яз. Образовано от чисти, чьту, перегласованной формы к чьсти, чъту-«почитать».
Этимологический словарь
Общеслав. Суф. производное (суф. -slo) от чисти «считать, читать» > *čitti (tt > ст), см. честь, читать.
число́
укр. число́, др.-русск. число, ст.-слав. число ἀριθμός (Остром., Супр.), сербохорв. чи́сло - то же, стар., словен. číslo, чеш. číslo, слвц. číslo, др.-польск. сzуsɫо, в.-луж. čisɫo, н.-луж. суsɫо.
Из праслав. *čit-slo, родственного чита́ть, честь; см. Бернекер I, 157. Наряду с этим - др.-русск. чисмС§, мн. чисмена, ст.-слав. чисмС© ἀριθμός (Супр.) Из *čit-smen-; см. И. Шмидт, KSchlBeitr. 7, 243; Бернекер, там же; Бругман, Grdr. 2, I, 242 и сл.; Сольмсен, Rhein. Мus. 56,497 и сл. [См. еще Вернадский, "Speculum", 29, 1954, стр. 335. - Т.]
Сканворды для слова число
- Октановое ...
- Грамматическая категория глагола.
- Комплексное ...
- То, чем берут без умения.
- «Он» - единственное, «они» - множественное.
- Какое сегодня ...?
- 13-е несчастливое.
- «Всыпать по первое ...».
- Элемент даты.
- День месяца.
- ... с плавающей запятой.
- Что означает греческое слово «arithmos», от которого произошла арифметика?
- Роман Роберта Хайнлайна «... зверя».
- Каким понятием пользовались последователи Пифагора для обозначения первоначала?
- Книга австрийского писателя Рудольфа Каснера «... и лицо».
- Фильм Пола МакГигана «Счастливое ... Слевина».
Полезные сервисы