ТРОЛЛЕЙ я, м. trolley m. <англ. trolley. Роликовый токоприемник электрического транспорта (троллейбуса, трамвая и т. п.). БАС-1. Уже Большая энциклопедия ( СПб., 1901, п. 1) писала: "В Америке были произведены, в самое последнее время удачные опыты движения электровагонов по шоссе, без рельсов, с применением приводов системы Trolley". Таким образом, в самом конце 1890 гг. в русском языке было введено английское (через французский язык, где слово зарегистрировано под 1896 г.). РР 1982 5 122. В 1900 году в "Журнале министерства путей сообщения".. предлагалось "применить самодвижущий троллей, подобный применяемому для электромобилей, троллею". Под словом "троллей" автор статьи имел в виду специальную небольшую тележку с электромотором, катящуюся по контактному проводу параллельно основному экипажу и связанную с его двигателем электрическим проводником. РР 1982 5 123. Был демонстрирован автомобиль. питаемый током от центральной станции при помощи особой тележки (троллея), катящегося по проводам, передвигается по проводам самим автомобилем. Автомобилист 1902. // НИЖ 2002 4 41. || Контактный провод, осуществляющий питание электродвигателя через роликовый токоприемник. БАС-1. Проверяя троллей на крановый путях, Геннадий .. чувствовал себя хозяином всего этого движущегося, работающего металла. Гранин После свадьбы. - Удар. В англ. яз. слово несет ударение на первом слоге. - Лекс. СИС 1937: тролле/й.

Составить слова из слова троллей

ДИНАМИКА - часть кинетики - раздела теоретической механики, в котором рассматриваются тела в условиях воздействия на них заданных сил. Кинетика подразделяется на статику и динамику. В статике рассматриваются тела в равновесии, т.е. в состоянии покоя или равномерного прямолинейного движения. В динамике же рассматриваются тела, скорость движения которых под действием сил изменяется либо по величине, либо по направлению (неравномерное или непрямолинейное движение).

СТАТИКА И РАВНОВЕСИЕ

Равновесие. Тело, находящееся в состоянии покоя или равномерного и прямолинейного движения, находится в равновесии. Равнодействующая всех сил, действующих на такое тело, равна нулю. Если на тело, находящееся в равновесии, действуют только две силы, то они должны быть равны по величине и противоположны по направлению, так как только в этом случае их равнодействующая равна нулю. На рис. 1 показаны два примера тела, находящегося в равновесии в условиях, когда на него действуют две силы: лампа, стоящая на столе, и лампа, висящая на потолке. На настольную лампу действуют направленная вниз сила тяжести W, т.е. ее вес, и направленная вверх сила сопротивления стола F. Поскольку лампа находится в состоянии покоя, сила F должна быть равна по величине и противоположна по направлению силе W. Точно так же в случае висящей лампы тянущая вниз сила W должна быть равна по величине и противоположна по направлению тянущей вверх силе F натяжения шнура, на котором она подвешена.

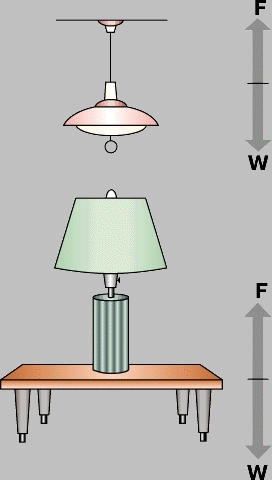
Рис. 1. РАВНОВЕСИЕ - состояние тела, в котором сумма всех сил, действующих на него, равна нулю. Тянущий вниз вес W как подвесной потолочной, так и настольной лампы уравновешивается направленной вверх силой F.

Разложение сил. Когда число сил, действующих на тело, находящееся в равновесии, больше двух, анализ несколько усложняется.

Например, если лампа подвешена между двумя столбами на разных расстояниях от них (рис. 2,а), то на нее действуют три силы - силы натяжения двух шнуров и вес лампы. Сила натяжения одного шнура F1 направлена вверх и влево, а другого, F2, - вверх и вправо, тогда как сила тяжести W тянет лампу вниз. Поскольку лампа находится в равновесии, равнодействующая всех сил, приложенных к ней, должна быть равна нулю. Следовательно, сумма вертикальных (направленных вверх) составляющих сил натяжения двух шнуров должна быть равна по величине (и противоположна по направлению) силе веса, а горизонтальные составляющие двух сил натяжения должны быть одинаковы по величине (и противоположно направлены). Это можно показать, разложив обе силы на составляющие по правилу параллелограмма сил. Согласно этому фундаментальному правилу физики, всякую силу можно разложить на горизонтальную и вертикальную составляющие, построив прямоугольник, для которого эта сила была бы диагональю (рис. 2,б). Горизонтальная и вертикальная стороны прямоугольника дадут горизонтальную и вертикальную составляющие силы соответственно. (И наоборот, если две силы приложены в одной точке, то, построив параллелограмм, двумя смежными сторонами которого являются эти две силы, можно найти их равнодействующую как диагональ параллелограмма.) Поскольку вертикальные составляющие обеих сил натяжения шнуров направлены вверх по одной линии, они складываются арифметически. Эта равнодействующая R двух вертикальных составляющих равна по величине и противоположна по направлению силе W (рис. 2,в). Горизонтальные составляющие сил, с которыми действуют на лампу два шнура, изображены как равные и противоположно направленные силы F1x и F2x.

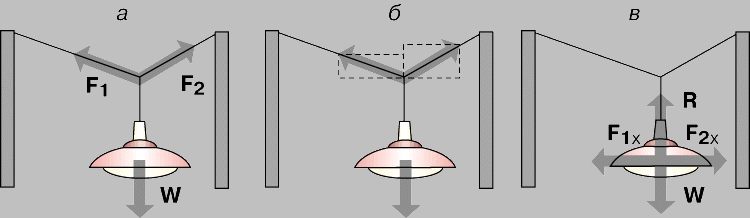
Рис. 2. РАЗЛОЖЕНИЕ СИЛ по правилу параллелограмма сил. a - лампа, подвешенная на шнурах на двух столбах; б - наклонные силы F1 и F2, действующие на лампу, разлагаются на горизонтальные и вертикальные составляющие построением на этих силах прямоугольников как на диагоналях; в - сумма вертикальных составляющих, их равнодействующая R, уравновешивает вес W, а горизонтальные составляющие F1x и F2x уравновешивают друг друга, так что лампа находится в равновесии.

Равновесие на наклонной плоскости. Если на наклонную плоскость положить брусок, то в отсутствие трения он соскользнет по ней вниз. Анализ действующих сил позволяет объяснить отсутствие равновесия в рассматриваемом случае. На брусок (рис. 3) действует только одна сила - его вес W. Ее можно разложить на две составляющие P и Q, одна из которых параллельна, а другая - перпендикулярна наклонной плоскости. Составляющая P, перпендикулярная наклонной плоскости, никак не влияет на движение по этой плоскости и уравновешивается направленной вверх по нормали силой реакции N. В то же время сила Q ничем не уравновешена и тянет брусок по наклонной плоскости вниз. Величина силы Q определяется, очевидно, двумя факторами - величиной силы W и крутизной наклона плоскости. Чем больше каждый из них, тем больше сила Q. Если бы плоскость не была наклонной, то сила P равнялась бы весу W, а силы Q не было бы вовсе. Если бы плоскость была вертикальной, то сила Q равнялась бы весу W и брусок свободно упал бы вниз. Чтобы брусок на наклонной плоскости был в равновесии, к нему должна быть приложена действующая вправо и вверх сила, равная по величине, но противоположная по направлению силе Q. Если наклонная плоскость не идеальна, т.е. существует трение, то на стремящийся соскользнуть вниз брусок действует сила трения, направленная в сторону, противоположную его движению. Таким образом, если сила трения равна силе Q, последняя уравновешивается и брусок остается неподвижно лежать на наклонной плоскости, а если сила трения меньше Q, то брусок будет скользить вниз, но медленнее, чем это было бы в отсутствие трения.

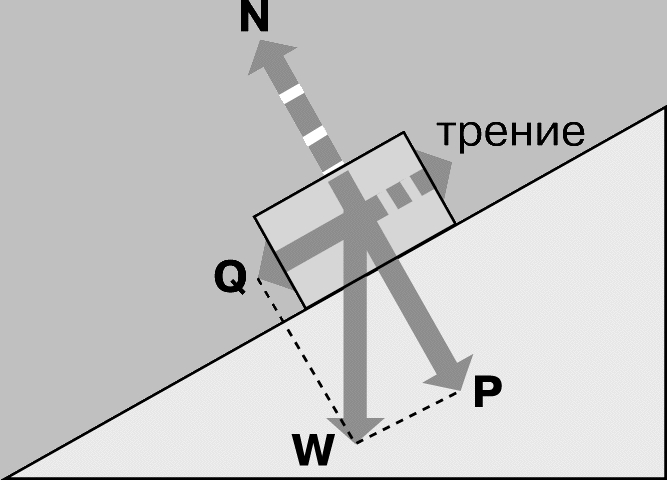
Рис. 3. РАВНОВЕСИЕ на наклонной плоскости. Перпендикулярная наклонной плоскости составляющая P веса бруска W уравновешивается нормальной реакцией N, а параллельная Q - силой трения между бруском и наклонной плоскостью.

Равновесие и вращение. Во всех рассмотренных примерах равновесия действующие силы не только были равны по величине и противоположны по направлению, но и лежали на одной прямой или проходили через одну точку. Если же на твердое тело действуют силы, которые нельзя свести к одной, то они заставляют тело вращаться. (Две параллельные силы, равные по величине и противоположно направленные, называются парой сил.) Для того чтобы тело в таких условиях было в равновесии, т.е. не вращалось, пара сил должна быть уравновешена двумя такими же силами, вращающими тело в другую сторону.

Момент силы. Если твердое тело закреплено в одной точке на шарнире и на него действует лишь одна сила, заставляющая его вращаться вокруг этой точки, то говорят, что тело вращается под действием момента силы. Момент силы равен произведению силы на ее плечо, т.е. на расстояние по перпендикуляру от точки закрепления до линии действия силы (рис. 4,а). Если на твердое тело действуют несколько сил, то тело не будет вращаться только при условии, что сумма моментов всех сил равна нулю (рис. 4,б).

См. также СТАТИКА.

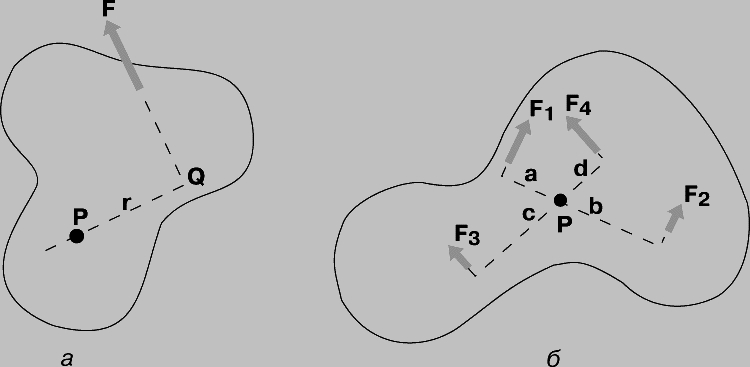
Рис. 4. МОМЕНТ СИЛЫ равен произведению силы F (рис. 4,а) на плечо силы, т.е. на расстояние (по перпендикуляру) PQ от точки P шарнирного закрепления тела до линии действия силы F. В случае нескольких сил, действующих на твердое тело, способное вращаться вокруг точки P (рис. 4,б), условием равновесия является равенство нулю суммы моментов всех сил:

[[F1*a]] + [[F2*b]] + [[F3*c]] + [[F4*d]] = 0.

Равномерное движение. Тело движется равномерно, если в любую единицу времени своего движения оно проходит одно и то же расстояние в одном и том же направлении. Примером прямолинейного равномерного движения может служить движение космического аппарата, летящего по инерции в межзвездном пространстве достаточно далеко от всех небесных тел, там, где гравитационные поля ничтожно малы. Коль скоро на него не действуют никакие внешние силы, он будет, не останавливаясь, двигаться по прямой линии с постоянной скоростью. Но как только космический аппарат приблизится к какому-либо небесному телу, он окажется в гравитационном поле этого тела и начнет с нарастающей скоростью отклоняться к нему от прямолинейной траектории. Если же в межзвездном пространстве он войдет в плотное облако космической пыли, то (если отвлечься от гравитационного воздействия пыли) он по-прежнему будет двигаться прямолинейно, но с замедлением. В обоих случаях изменение характера движения вызывается действием неуравновешенных внешних сил.

ДИНАМИКА

Динамика изучает тела, находящиеся под воздействием неуравновешенных внешних сил, т.е. тела, характер движения которых изменяется. Поскольку равновесие означает равенство нулю равнодействующей всех сил, приложенных к телу, динамика, очевидно, имеет дело с силами, равнодействующая которых не равна нулю. Английский физик и математик И. Ньютон (1643-1727) сформулировал три закона движения, которым подчиняются тела, движущиеся под действием неуравновешенных сил, и за этими законами навсегда закрепилось его имя.

Первый закон Ньютона. Всякое тело сохраняет свое состояние покоя или равномерного и прямолинейного движения, пока неуравновешенные внешние силы не заставят его изменить это состояние. Поскольку состояние покоя, как и состояние равномерного и прямолинейного движения, соответствует равновесию, из первого закона Ньютона следует, что тело, находящееся в равновесии, остается в равновесии, пока его не выведут из этого состояния внешние силы.

Инерция. Если для того, чтобы изменить состояние покоя или равномерного и прямолинейного движения, нужна внешняя сила, то, очевидно, что-то противодействует такому изменению. Свойственная всем телам способность сопротивляться изменению состояния покоя или движения называется инертностью или инерцией. Когда приходится толкать автомобиль, то вначале нужно больше усилий, чтобы стронуть его с места, чем потом - чтобы поддерживать его качение. Здесь инерция проявляется двояким образом. Во-первых, как сопротивление переходу из состояния покоя в состояние движения. Во-вторых, если дорога ровная и гладкая, то как стремление катящегося по ней автомобиля сохранить свое состояние движения. В такой ситуации всякий может сам ощутить инерцию автомобиля, попробовав его остановить. Для этого потребуется гораздо больше усилий, чем для поддержания движения.

Второй закон Ньютона. Всякое тело, на которое действует постоянная сила, движется с ускорением, пропорциональным силе и обратно пропорциональным массе тела. Самый обычный пример второго закона Ньютона - падение какого-либо тела на землю. Движение в направлении к земле вызывается силой гравитационного притяжения, которая при малой высоте падения практически постоянна. Поэтому за каждую секунду падения тела его скорость увеличивается на 9,8 м/с. Таким образом, падающее тело движется с ускорением, равным 9,8 м/с2. Второй закон Ньютона записывается в виде алгебраического соотношения F = ma, где F - сила, приложенная к телу, m - масса тела и a - ускорение, вызываемое силой F.

Импульс (количество движения). Количеством движения тела называется произведение его массы m на его скорость v, т.е. величина mv. Количество движения одинаково у автомобиля массой 1 т, мчащегося со скоростью 100 км/ч, и у 2-тонного грузовика, едущего в том же направлении со скоростью 50 км/ч. Поскольку ускорение есть изменение скорости за малое время t, второй закон Ньютона можно переписать в виде mv = Ft. Произведение силы F на (малое) время ее действия t ранее называлось импульсом силы. Поэтому количество движения в настоящее время называют импульсом. Для импульса (количества движения) справедлив закон сохранения: при столкновении двух или нескольких тел их полный (суммарный) импульс не изменяется. Например, при забивании гвоздя молотком полный импульс молотка и гвоздя после удара равен полному импульсу молотка до удара (поскольку импульс гвоздя до удара был равен нулю).

Третий закон Ньютона. Для всякой силы действия имеется равная, но противоположно направленная сила противодействия. Иначе говоря, всякий раз, когда одно тело действует с какой-либо силой на другое, последнее тоже действует на него с такой же по величине, но противоположно направленной силой. Примером может служить отдача винтовки при выстреле. Винтовка действует на пулю с силой, направленной вперед, а пуля на винтовку - с силой, направленной назад. В результате пуля летит вперед, а винтовка отдает в плечо стрелку. Если силу, приложенную к пуле, считать действием, то отдача будет противодействием (реакцией). Другой пример к третьему закону - реактивное движение ракеты. Здесь действием считается истечение струи газов из сопла двигателя, а противодействием (реакцией) - движение ракеты в направлении, противоположном движению газов.

Центростремительная сила. Когда вращают мяч на бечевке (рис. 5), бечевка тянет его в сторону центра вращения. Сила, направленная к центру вращения, называется центростремительной. Инерция мяча (его стремление продолжать в каждый момент движение по прямой линии) заставляет бечевку натягиваться. Поскольку мяч продолжает вращаться по окружности, его инерция создает равную, но противоположно направленную, так называемую центробежную силу. Если мяч движется по окружности с постоянной скоростью, то может показаться, что он находится в равновесии относительно центра окружности. Но это неверно. На самом деле мяч приобретает ускорение, направленное к центру вращения, хотя и остается все время на одном и том же расстоянии от центра. Этот кажущийся парадокс поясняется рис. 6. Здесь кривая AB - часть круговой траектории мяча, а прямая AC - касательная (к окружности), по которой полетел бы мяч, если бы бечевка лопнула и он двигался по инерции. Длина отрезков s, t, u и w, соединяющих дугу и прямую, увеличивается в направлении движения. Чтобы мяч продолжал двигаться по дуге окружности, некая непрерывно действующая сила F должна приводить его в движение с возрастающей скоростью. Необходимое ускорение сообщает ему центростремительная сила.

См. также

МАШИНЫ И МЕХАНИЗМЫ;

МЕХАНИКА.

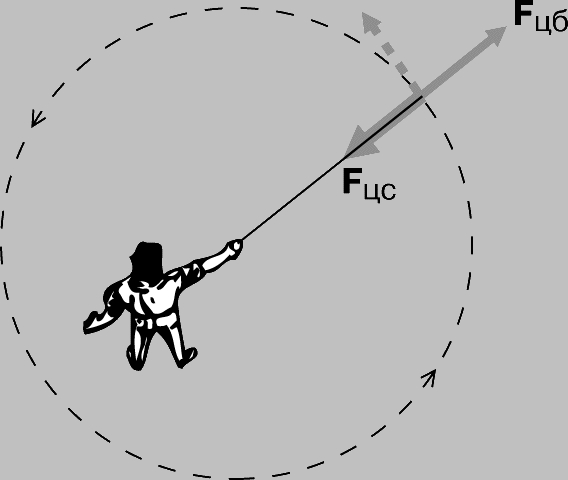
Рис. 5. ДВИЖЕНИЕ ТЕЛА ПО ОКРУЖНОСТИ. Fцс - центростремительная сила; Fцб - центробежная сила; штриховой стрелкой показано направление движения по инерции. Центростремительная сила увлекает тело с пути, соответствующего прямолинейному движению по инерции. Сила сопротивления этому увлечению называется центробежной силой.

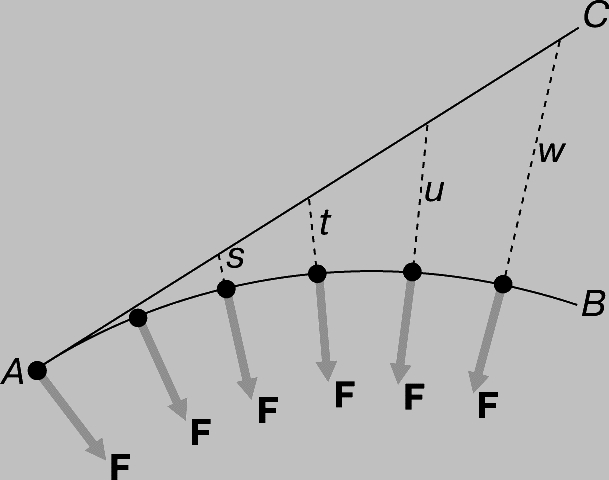
Рис. 6. УСКОРЕНИЕ, приобретаемое телом при движении по окружности. Двигаясь под действием центростремительной силы F по кривой AB, тело все больше удаляется от прямой AC (увеличиваются отклонения s, t, u, w).

ЛИТЕРАТУРА

Халфмэн Р. Динамика. М., 1972 Татаринов Я.В. Лекции по классической динамике. М., 1984 Ньютон И. Определения. Аксиомы и законы движения. М., 1985 Бабенков И.С. Основы статики и сопротивления материалов. М., 1988

Составить слова из слова динамика

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ - раздел геометрии, который исследует простейшие геометрические объекты средствами элементарной алгебры на основе метода координат. Создание аналитической геометрии обычно приписывают Р.Декарту, изложившему ее основы в последней главе своего трактата Рассуждение о методе, озаглавленной Геометрия (1637). Однако сам метод был известен П.Ферма еще в 1629, о чем свидетельствует его переписка. Аналитическая геометрия стала неоценимым подспорьем для математического анализа, изобретенного вскоре Ньютоном (1665-1666) и Лейбницем (1675-1676). Методы аналитической геометрии применимы к фигурам на плоскости и к поверхностям в трехмерном пространстве, а также допускают естественное обобщение и на пространства более высоких размерностей. Мы начнем с аналитической геометрии на плоскости. Сущность метода координат состоит в следующем. На плоскости задаются две взаимно перпендикулярные прямые (координатные оси), пересекающиеся в точке О, называемой началом координат. Одна из них - ось x, или ось абсцисс, обычно выбирается горизонтальной, другая - ось y, или ось ординат, - вертикальной. Справа от O выбирается точка, у которой ставится отметка 1. Если принять отрезок от O до 1 за единицу длины, то откладывая последовательно этот отрезок вдоль прямой, мы получаем числовую ось. Считается, что эта ось продолжается вправо до бесконечности. Точки на оси x слева от O помечаются отрицательными числами, как на шкале термометра. Например, точка -2 расположена от точки O слева на таком же расстоянии, как точка 2 справа. Аналогичным образом с той же единицей длины размечается и ось y. Положительные числа располагаются выше точки O, отрицательные - ниже. Пусть P - любая точка на плоскости с заданной системой координат, Q - основание перпендикуляра, опущенного из P на ось x, а R - основание перпендикуляра, опущенного из P на ось y. Положение точки P полностью определяется двумя числами, называемыми координатами x и y. Первая координата указывает положение точки Q на оси x, вторая - положение точки R на оси y. На рис. 1 положение точки P полностью определяется ее координатами (2,3).

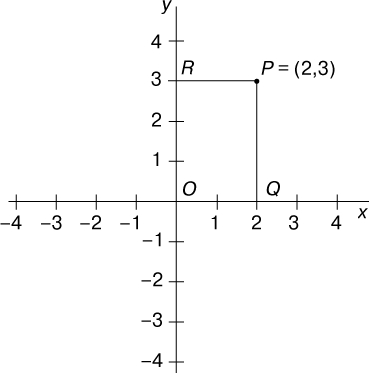
1. ДВЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ, называемые осью x и осью y, составляют основу для большинства операций в аналитической геометрии на плоскости. Именно они позволяют использовать алгебраические средства в геометрии и геометрические - в алгебре. Будучи снабженными шкалами, они представляют координаты точки. Например, точка P имеет координату x, равную 2, и координату y, равную 3.">

Рис. 1. ДВЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ, называемые осью x и осью y, составляют основу для большинства операций в аналитической геометрии на плоскости. Именно они позволяют использовать алгебраические средства в геометрии и геометрические - в алгебре. Будучи снабженными шкалами, они представляют координаты точки. Например, точка P имеет координату x, равную 2, и координату y, равную 3.

Основная задача аналитической геометрии заключается в изучении геометрических фигур с помощью соотношений между координатами точек, из которых эти фигуры образованы. Любую фигуру можно рассматривать как множество точек, удовлетворяющих некоторому геометрическому условию. Это условие можно записать в виде алгебраического уравнения, связывающего координаты x и y каждой точки фигуры. Суть метода аналитической геометрии состоит в изучении свойств фигуры с помощью соответствующего уравнения, исследуемого средствами алгебры. Этот метод позволяет устанавливать геометрические факты систематичным образом, в отличие от традиционной "синтетической" геометрии, где приходилось изобретать методы доказательства для каждого отдельного случая. Основным инструментом аналитической геометрии служит формула для вычисления расстояния между двумя точками P1 = (x1,y1) и P2 = (x2,y2). Числа x1, y1, x2 и y2 могут быть любыми действительными числами, положительными, отрицательными или 0. На рис. 2 все числа выбраны положительными. Проведем через точку P1 горизонтальную прямую, а через точку P2 - вертикальную. Пусть R - точка их пересечения. Тогда по теореме Пифагора

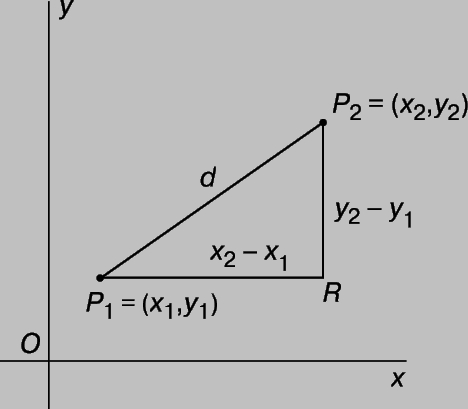
Рис. 2. РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ можно найти, если построить прямоугольный треугольник с катетами, параллельными осям координат. Расстояние между точками P1 и P2 устанавливается по теореме Пифагора.

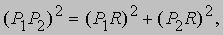
откуда d 2 = (x2 - x1)2 + (y2 - y1)2. Это и есть формула для вычисления расстояния между двумя точками. Важно иметь в виду, что эта формула остается в силе независимо от того, как расположены точки P1 и P2. Например, если точка P2 расположена ниже точки P1 и справа от нее, как на рис. 3, то отрезок RP2 можно считать равным y1 - y2, а не y2 - y1. Расстояние между точками, вычисляемое по формуле, от этого не изменится, так как (y1 - y2)2 = (y2 - y1)2. Заметим, что так как величина y2 в этом случае отрицательна, разность y1 - y2 больше, чем y1, как и должно быть.

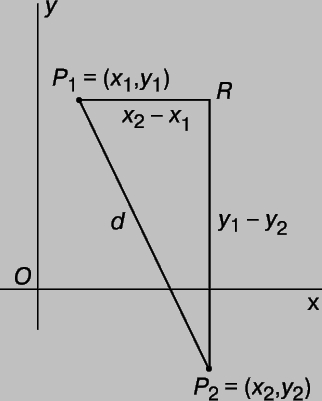
Рис. 3. ФОРМУЛА ДЛЯ ВЫЧИСЛЕНИЯ РАССТОЯНИЯ не изменяется, если одна из точек имеет отрицательные координаты, так как величина (y1 - y2)2 положительна, даже если величина (y1 - y2) отрицательна.

Прямые. Прямая - одна из простейших геометрических фигур. Алгебраическое уравнение прямой также имеет простой вид. Пусть B = (0,b)- точка пересечения прямой L с осью y, а P = (x,y) - любая другая точка на этой прямой. Проведем через точку B прямую, параллельную оси x, а через точку P - прямую, параллельную оси y; проведем также прямую x = 1. Пусть m - угловой коэффициент прямой L (см. рис. 4). Так как треугольники BSQ и BRP подобны, то

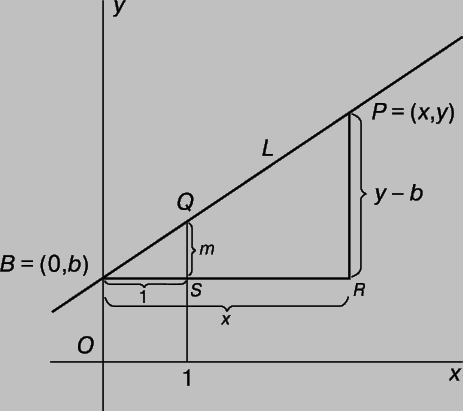
Рис. 4. ЛЮБАЯ НЕВЕРТИКАЛЬНАЯ ПРЯМАЯ, например L, определяется заданием точки, в которой она пересекает ось y (точка b) и угловым коэффициентом m, определяемым отношением (y - b)/x, или расстоянием QS по вертикали при x = 1.

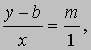
или, после упрощения,

Следовательно, если точка P лежит на прямой L, то ее координаты удовлетворяют уравнению (1). Обратно, нетрудно показать, что если x и y связаны между собой уравнением (1), то точка P непременно лежит на прямой L, проходящей через точку (0,b) и имеющей угловой коэффициент m. Таким образом, уравнение любой прямой можно записать в виде

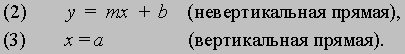
В обоих случаях мы получаем уравнение первой степени. Кроме того, каждое уравнение первой степени по x и y можно привести к виду (2) либо (3). Рассмотрим произвольное уравнение первой степени

Если B № 0, мы можем записать уравнение (4) в виде

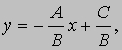
т.е. в виде (2). При B = 0 уравнение (4) сводится к уравнению Ax = C, или

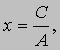
т.е. к уравнению вида (3). Таким образом, любая прямая описывается уравнением первой степени по x и y, и обратно, каждое уравнение первой степени по x и y соответствует некоторой прямой.

Парабола. Методы аналитической геометрии позволяют без особых трудностей исследовать свойства кривых, которые обычно не рассматриваются в стандартных учебниках планиметрии. Пусть заданы точка F с координатами (0,1) и прямая y = -1 (рис. 5). Множество точек P = (x,y), для которых расстояние PF равно расстоянию PD, называется параболой. Прямая y = -1 называется директрисой параболы, а точка F - фокусом параболы. Чтобы выяснить, как располагаются точки P, удовлетворяющие условию PF = PD, запишем его с помощью координат:

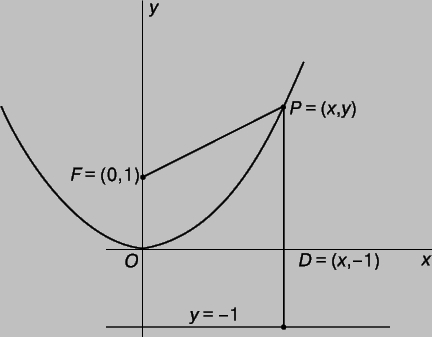
Рис. 5. ПОСТРОЕНИЕ ПАРАБОЛЫ - траектории точки P, равноудаленной от заданной точки, например F, и прямой, например y = -1.

x2 + (y - 1)2 = (y + 1)2 + (x - x)2, или после упрощения x2 = 4y. Это уравнение геометрического места точек, образующих параболу. Рассмотрим теперь точки пересечения произвольной невертикальной прямой y = mx + b с параболой x2 = 4y. Точки пересечения должны иметь координаты, удовлетворяющие одновременно обоим уравнениям, поэтому x2 = 4mx + 4b, или x2 - 4mx - 4b = 0. В общем случае существуют два решения x1 и x2 квадратного уравнения. Известно, что сумма этих решений x1 + x2 равна коэффициенту при x, взятому со знаком минус. Следовательно, x1 + x2 = 4m. Абсцисса средней точки M хорды P1P2 равна

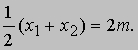
Результат зависит только от m и не зависит от b. Если теперь мы рассмотрим множество параллельных прямых с одним и тем же угловым коэффициентом m, но с различными значениями b, то середины всех хорд, высекаемых на этих прямых параболой, лежат на вертикальной прямой x = 2m (см. рис. 6).

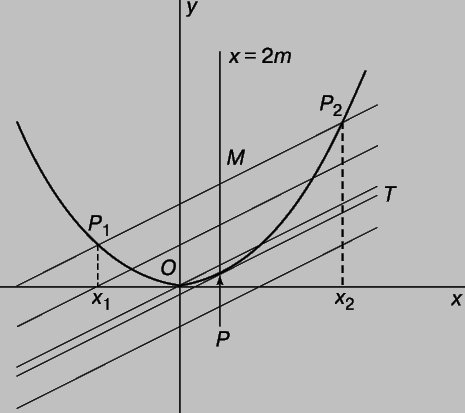
Рис. 6. ПАРАБОЛА, симметричная относительно оси y, пересечена семейством параллельных прямых с угловым коэффициентом m. Середины всех хорд, отсекаемых от этих прямых параболой, лежат на вертикальной прямой x = 2m. Касательная T к параболе пересекает ее в единственной точке P с координатами (2m,m2).

Среди этих параллельных прямых есть одна особенная прямая T, пересекающая параболу только в одной точке. Эта прямая называется касательной. Точка касания P имеет координаты (2m,m2).

Преобразование уравнений. Уравнение кривой зависит от положения координатных осей и от выбранных масштабов. Например, уравнение окружности с радиусом r единиц и с центром в начале координат имеет вид x2 + y2 = r2. Но если окружность расположена так, как показано на рис. 7, с центром в точке с координатами (h,k), то ее уравнение принимает более сложный вид:

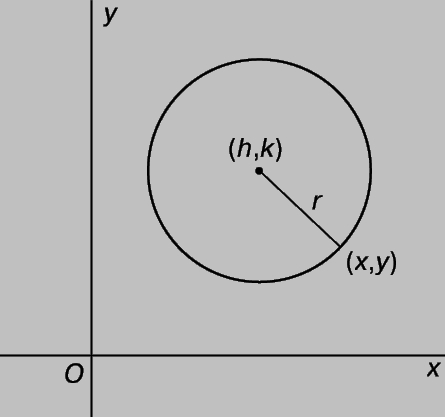
Рис. 7. ПРЕОБРАЗОВАНИЕ уравнений, связанное с различным расположением системы координат. Окружность с центром в точке (h,k) имеет иное уравнение, чем окружность с центром в начале координат O.

(x - h)2 + (y - k)2 = r2, в чем нетрудно убедиться, воспользовавшись формулой расстояния. Для исследования свойств кривой удобно расположить оси так, чтобы уравнение приняло по возможности более простой вид, как мы поступили в случае параболы. До сих пор мы исследовали кривую, заданную некоторым геометрическим условием, которому должны удовлетворять все принадлежащие ей точки, и вывели уравнение относительно заданной пары координатных осей. Обратная задача состоит в том, чтобы построить кривую, соответствующую данному уравнению, и исследовать геометрические свойства этой кривой или ее графика. Предположим, что мы хотим исследовать график кривой

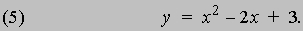
Перепишем это соотношение в виде y = x2 - 2x + 1 + 2 = (x - 1)2 + 2. Сделав затем замену переменных xў = x - 1 и yў = y - 2, сведем (5) к следующему уравнению:

которое, конечно, гораздо проще. Теперь заданную кривую можно записать в новой системе, оси которой параллельны старым с началом координат в точке x = 1, y = 2. Помимо такого приема (называемого параллельным переносом) - сдвига осей координат по горизонтали и по вертикали на соответствующие величины, уравнения часто упрощаются после поворота системы координат на некоторый угол вокруг неподвижного начала координат O. Оказывается, что этих двух приемов - параллельного переноса и поворота координатных осей, выполняемых по отдельности или вместе, - вполне достаточно, чтобы привести уравнение второй степени или к уравнениям двух прямых (пересекающихся, параллельных или совпадающих) или к одному из стандартных видов:

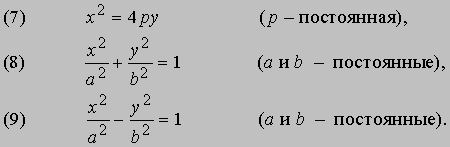
Уравнение (7) описывает параболу с фокусом в точке (0,p) и директрисой y = - p. Уравнение (8) соответствует эллипсу. Уравнение (9) описывает гиперболу (см. также КОНИЧЕСКИЕ СЕЧЕНИЯ). Помимо исследования графиков алгебраических уравнений, аналитическая геометрия изучает также неалгебраические, или трансцендентные, кривые, например графики экспоненциальных, логарифмических и тригонометрических функций. В качестве примера трансцендентной кривой приведем циклоиду - кривую, описываемую точкой окружности, катящейся без скольжения по прямой (рис. 8). Если в качестве прямой выбрать ось абсцисс, а радиус окружности принять равным 1, то координаты точки P будут иметь вид

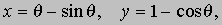
где q - угол в радианах.

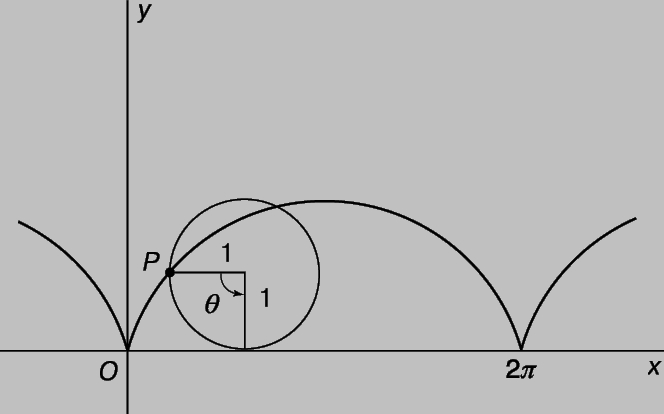
Рис. 8. ЦИКЛОИДА, кривая, определяемая как траектория точки окружности, катящейся по прямой без скольжения.

Циклоида обладает многими замечательными свойствами. Длина дуги циклоиды в 8 раз больше, чем длина катящейся окружности, а площадь под дугой в 3 раза больше площади катящегося круга. Если циклоиду перевернуть, то мы получим форму нити, по которой бусина соскальзывала бы до данной точки за кратчайшее время. Эти результаты доказываются методами математического анализа, а последний из них - методами вариационного исчисления. Циклоиды и аналогичные кривые, возникающие при движении одной окружности по другой, играют важную роль при проектировании зубчатых передач, действующих бесшумно и эффективно. На рис. 9 вы видите несколько других кривых и их уравнения.

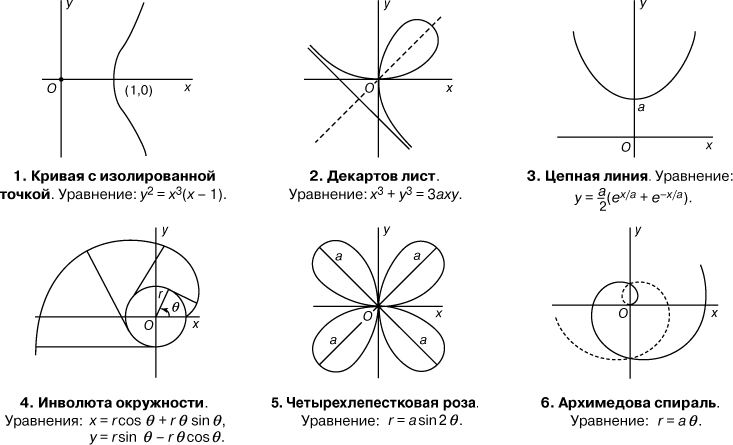
Рис. 9. РАЗЛИЧНЫЕ КРИВЫЕ и их уравнения.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

Методами аналитической геометрии исследуются также и пространственные фигуры. Нужно лишь воспользоваться тремя взаимно перпендикулярными осями, проходящими через начало координат О. Снабдив каждую ось шкалой, можно задать тремя числами (координатами) положение точки в пространстве. Например (рис. 10), P = (1,2,3).

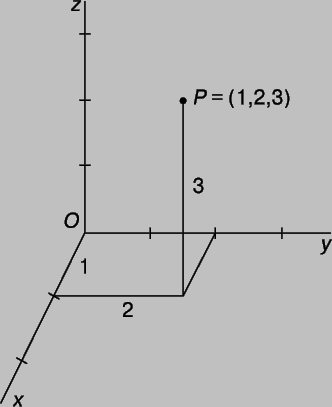
Рис. 10. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ требует трех взаимно перпендикулярных координатных осей и трех координат для задания положения точки. Точка P имеет координаты (1,2,3).

Множеству точек, удовлетворяющих некоторому геометрическому условию, соответствует определенное алгебраическое соотношение между их координатами x, y, z. Для задания этого соответствия необходима фундаментальная формула, определяющая расстояние d между точками P1 = (x1, y1, z1) и P2 = (x2, y2, z2), а именно: d2 = (x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2. Эта формула представляет собой обобщение теоремы Пифагора с двумерного случая на трехмерный. Из нее следует, что сфера радиуса r с центром в начале координат описывается уравнением x2 + y2 + z2 = r2. Любая плоскость задается уравнением первой степени относительно x, y и z, т.е. уравнением вида Ax + By + Cz = D, где A, B, C и D - постоянные и, по крайней мере, один из коэффициентов A, B или C не равен нулю. Помимо сферы есть и другие поверхности, также описываемые уравнением второй степени относительно x, y и z. Одна из задач аналитической геометрии в трехмерном пространстве состоит в том, чтобы дать классификацию таких квадратичных поверхностей и, исходя из соответствующих им уравнений, исследовать их свойства. Эти поверхности называются эллипсоидами, параболоидами, гиперболоидами или коническими и цилиндрическими поверхностями различных типов. Особенно простой подкласс этих фигур состоит из поверхностей, получаемых при вращении конических сечений вокруг различных осей симметрии. Существуют многочисленные поверхности, задаваемые уравнениями более высокого порядка. Как правило, они довольно сложны. Их изучением, как и плоских кривых высокого порядка, занимается алгебраическая геометрия. Как и в случае фигур на плоскости, исследование трехмерных геометрических тел часто облегчается подходящим выбором координатных осей. Соответствующее уравнение обычно удается упростить с помощью параллельного переноса и (или) поворота осей. Иногда бывает удобно воспользоваться непрямоугольной системой координат. Например, если в уравнение, записанное в прямоугольных координатах x, y и z, подставить x = r cos q, y = r sin q и z = z, то получится эквивалентное и нередко более простое уравнение в цилиндрических координатах r, q и z (рис. 11). Так, уравнение z = x2 + y2 сводится к уравнению z = r2.

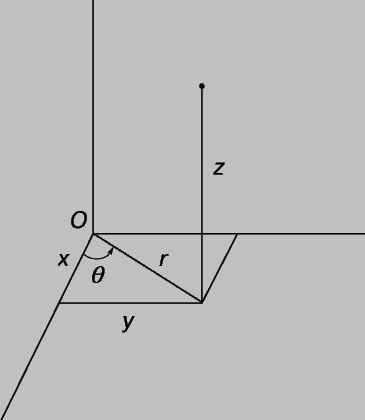
Рис. 11. ЦИЛИНДРИЧЕСКИЕ КООРДИНАТЫ иногда используются в геометрии трехмерного пространства для упрощения уравнений. Прямоугольные координаты x и y в этом примере заменены полярными r и q, а координата z оставлена без изменений.

Подстановка x = r cos q sin f, y = r sin q sin f, z = r cos f преобразует уравнение, заданное в прямоугольных координатах, в уравнение в сферических координатах r, q и f (рис. 12).

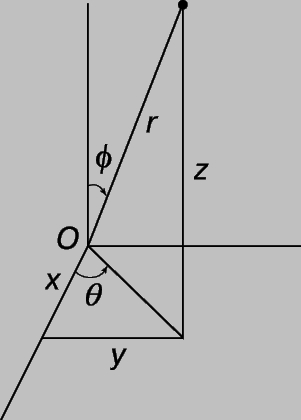
Рис. 12. СФЕРИЧЕСКИЕ КООРДИНАТЫ - трехмерный аналог полярных координат на плоскости. Положение точки однозначно определяется заданием расстояния r и двух углов - q, отсчитываемого от оси x, и f, отсчитываемого от оси z.

Аналитическая геометрия занимается также изучением прямых и кривых в трехмерном пространстве. Прямую можно рассматривать как линию пересечения подходящей пары плоскостей. Соответственно, пространственную прямую можно задать с помощью двух уравнений первого порядка. Однако часто бывает проще задать прямую L с помощью параметра t следующим образом: x = x0 + a1t, y = y0 + a2t, z = z0 + a3t. Когда t принимает все возможные действительные значения, мы получаем все возможные значения x, y и z для точек на L. При t = 0 мы получаем координаты x0, y0 и z0 некоторой точки P0; при t = 1 - координаты (x0 + a1, y0 + a2, z0 + a3) некоторой другой точки P1. Прямая L определяется двумя своими точками P0 и P1. Пространственную кривую можно также записать в виде x = f1(t), y = f2(t), z = f3(t), где f1, f2 и f3 - заданные функции. (Прямая соответствует случаю, когда все три функции имеют первую степень по t.) Например, x = cos t, y = sin t, z = t - уравнения винтовой линии, получающейся при наматывании нити на цилиндрическую поверхность радиуса 1 с постоянным шагом (рис. 13).

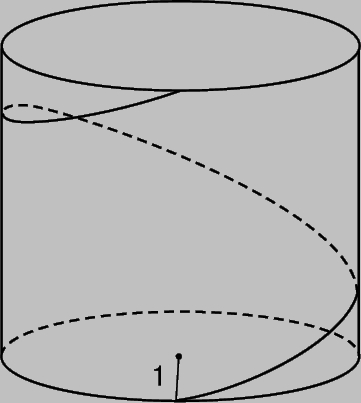
Рис. 13. ВИНТОВАЯ ЛИНИЯ, пространственная кривая, задаваемая радиусом и расстоянием между точками пересечения кривой с любой вертикальной прямой на поверхности цилиндра того же радиуса.

Более высокие размерности. Вполне естественно обобщить методы аналитической геометрии на случаи, когда число координат больше трех. Разумеется, невозможно представить себе наглядно гиперсферу x2 + y2 + z2 + w2 = r2 или гиперплоскость Ax + By + Cz + Dw = E. И все же мы можем воспользоваться теми же алгебраическими методами, как и в случаях двух или трех измерений, используя соответствующий им наглядный геометрический язык как подсказку, когда такая наглядность отсутствует. Более того, весьма плодотворным оказалось обобщение методов аналитической геометрии на бесконечномерные пространства. Многие важные разделы аналитической геометрии пространства трех и более измерений можно существенно упростить с помощью векторных методов (см. также ВЕКТОР).

ЛИТЕРАТУРА

Погорелов А.В. Аналитическая геометрия. М., 1978 Ильин В.А., Позняк Э.Г. Аналитическая геометрия. М., 1981

Составить слова из слова аналитическая геометрия