КО́МПЛЕКС, -а, м.
комплексное картографирование
Энциклопедический словарь
Ко́мплексное картографи́рование - многостороннее отображение на картах природных и социально-экономических явлений с учётом их взаимосвязей; осуществляется путём создания серии взаимосвязанных тематических карт или их целостного набора (например, атлас).
* * *
КОМПЛЕКСНОЕ КАРТОГРАФИРОВАНИЕ - КО́МПЛЕКСНОЕ КАРТОГРАФИ́РОВАНИЕ, многостороннее отображение на картах природных и социально-экономических явлений с учетом их взаимосвязей; осуществляется путем создания серии взаимосвязанных тематических карт (см. ТЕМАТИЧЕСКИЕ КАРТЫ) или их целостного набора (напр., атлас (см. АТЛАС) ).
Большой энциклопедический словарь
КОМПЛЕКСНОЕ КАРТОГРАФИРОВАНИЕ - многостороннее отображение на картах природных и социально-экономических явлений с учетом их взаимосвязей; осуществляется путем создания серии взаимосвязанных тематических карт или их целостного набора (напр., атлас).
Полезные сервисы
комплексное число
Энциклопедический словарь
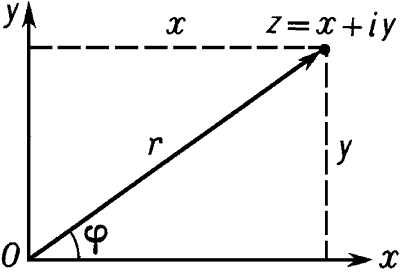
Ко́мпле́ксное число́ - число вида х + iy, где х и у - действительные числа, а i - так называемая мнимая единица (число, квадрат которого равен -1); х называется действительной частью, а у - мнимой частью комплексного числа. Действительные числа - частный случай комплексного числа (при у = 0). Комплексные числа, не являющиеся действительными (у ≠ 0), иногда называются мнимыми числами, при х = 0 комплексные числа называются чисто мнимыми. Геометрически каждое комплексное число х + iy изображается точкой плоскости, имеющей прямоугольные координаты х и у (см. рис.). Если полярные координаты этой точки обозначить через r и φ, то соответствующее комплексное число можно представить в виде: r(cosφ + isinφ) (тригонометрическая форма комплексного числа),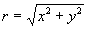 
х + iy, а φ - его аргументом, или в виде reiφ (показательная форма комплексного числа).
* * *
КОМПЛЕКСНОЕ ЧИСЛО - КО́МПЛЕ́КСНОЕ ЧИСЛО́, число вида x + iy, где х и y - действительные числа, а i - т. н. мнимая единица (число, квадрат которого равен -1); х называется действительной частью, а y - мнимой частью комплексного числа. Действительные числа - частный случай комплексных чисел (при y = 0). Комплексные числа, не являющиеся действительными (y № 0), иногда называются мнимыми числами, при х = 0 комплексные числа называются чисто мнимыми. Геометрически каждое комплексное число x + iy изображается точкой плоскости, имеющей прямоугольные координаты х и y. Если полярные координаты этой точки обозначить через r и j, то соответствующее комплексное число можно представить в виде: r (cosj+i sinj) (тригонометрическая форма комплексного числа); называется модулем комплексного числа x+iy, а = j - arctg(y/x) его аргументом, или в экспоненциальном виде: r eij
Большой энциклопедический словарь
КОМПЛЕКСНОЕ число - число вида x + iy, где х и y - действительные числа, а i - т. н. мнимая единица (число, квадрат которого равен ?1); х называется действительной частью, а y - мнимой частью комплексного числа. Действительные числа - частный случай комплексных чисел (при y = 0). Комплексные числа, не являющиеся действительными (y ? 0), иногда называются мнимыми числами, при х = 0 комплексные числа называются чисто мнимыми. Геометрически каждое комплексное число x + iy изображается точкой плоскости, имеющей прямоугольные координаты х и y. Если полярные координаты этой точки обозначить через r и ?, то соответствующее комплексное число можно представить в виде: r (cos?+i sin?) (тригонометрическая форма комплексного числа); называется модулем комплексного числа x+iy, а = ? ? arctg(y/x) его аргументом, или в экспоненциальном виде: r ei?
Идеография
▲ число
комплексное число.
мнимое число - результат извлечения корня.
тензор (# инерции. # диэлектрической проницаемости).
тензорный.
спинор. | гиперкомплексные числа.
кватернион.
↓ вектор