Исчисление конечных разностей связано с изучением свойств и применений разностей между соседними членами какой-нибудь последовательности или между значениями функции в точках, расположенных с постоянным интервалом в некотором пространстве. Слово "конечные" используется здесь в несколько устаревшем смысле "не бесконечно малые", т.е. не связанные с предельными переходами. Поскольку дифференциальное исчисление занимается изучением пределов разностей, а исчисление конечных разностей - самими разностями, то естественно, что между этими двумя теориями существуют много параллелей. Исчисления конечных разностей используются при интерполяции в математических таблицах, при суммировании числовых рядов, при вычислении интегралов и дифференцировании функций. Разности встречаются также в любой ситуации, когда надо описать поведение объекта, который испытывает воздействие меняющихся условий на определенном расстоянии (во времени и в пространстве). Например, термостату требуется значительное время, чтобы отреагировать на изменение температуры, поэтому он реагирует не на текущую температуру, а на ту, что была минуту назад. Другой пример: автомашиной управляет водитель, которому требуется какое-то время, чтобы отреагировать на возникшую на дороге ситуацию. Под конечной разностью первого порядка функции f (x) принято понимать величину
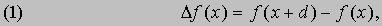
где d - некоторая постоянная, которую часто, но не всегда, принимают равной 1. Разность второго порядка обозначается D2f и представляет собой разность разностей, т.е.
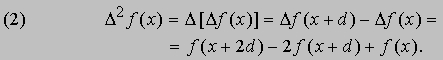
Продолжив этот процесс, мы получим разности более высоких порядков D3f (x), D4f (x), ј . Данные выше определения можно также применить к членам любых последовательностей величин, например, к последовательности 3, 6, 11, 18, 27, 38, ј.
Первые разности равны 6 - 3, 11 - 6, 18 - 11, 27 - 18, 38 - 27, ј, т.е. 3, 5, 7, 9, 11, ј; разности второго порядка постоянны и равны 2. В общем виде такие последовательности можно записать как
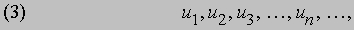
где разности первого, второго и т.д. порядков определяются выражениями
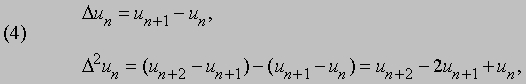
а n может принимать любое допустимое для индекса значение. В некоторых приложениях используются последовательности вида
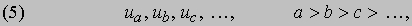
где индексы могут принимать любые убывающие значения. В этом случае вместо символа D используется символ
 разделенной разности.
разделенной разности.
Разделенные разности первого и второго порядков определяются следующим образом:
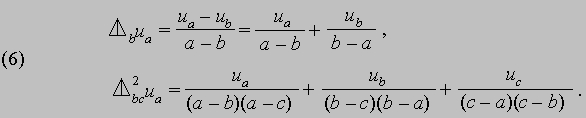
Помимо уже названных выше приложений, исчисление конечных разностей используется в страховании, теории вероятностей и статистике. В последние годы с изобретением быстродействующих компьютеров конечные разности стали все более широко применяться при решении дифференциальных уравнений, обыкновенных и в частных производных, многие из которых ранее было невозможно решить другими математическими методами.
У истоков теории. Хотя исследование свойств и использование конечных разностей приходится на современный период развития математики, Птолемей (ок. 150 н.э.) ввел в Альмагесте таблицу разностей первого порядка, чтобы облегчить расчеты в таблице длин хорд. Разности второго порядка использовал при вычислении своих таблиц логарифмов в 1624 Г. Бриггс. Теория интерполяции берет начало со знаменитой пятой леммы из 3-й книги Математических начал (1687) И. Ньютона, в которой впервые была приведена формула, носящая ныне его имя. Частный случай формулы Ньютона, открытый также независимо его современником Дж. Грегори (1638-1675), приведен ниже (см. формулу (7)). В общей формуле интерполяции Ньютона использовались разделенные разности, хотя этот термин, по-видимому, был введен О.де Морганом (1806-1871) в 1848. Первое применение исчисления конечных разностей к задачам теории вероятностей принято связывать с именами П.де Монтмора (1678-1719) и А. де Муавра (1667-1754). Хотя Л. Эйлер (1707-1783) в своих работах по дифференциальному исчислению использовал предельные переходы в конечных разностях, основания современной теории конечных разностей были заложены в основном Ж.Лагранжем (1736-1813) и П. Лапласом (1749-1827). Первый из них ввел в исчисление конечных разностей символические методы, второй сделал конечные разности главным инструментом в своей Аналитической теории вероятностей (1812). Под влиянием этих работ математики 19 в. принялись интенсивно разрабатывать предмет, и в 1860 Дж. Буль выпустил свой классический Трактат об исчислении конечных разностей. С тех пор это исчисление и круг его приложений существенно расширились. Одно из наиболее важных приложений конечные разности нашли в статистике. Особенно полезными они оказались в теории сериальной корреляции, в анализе случайных последовательностей и статистических временных рядов.
Интерполяция. Чтобы понять, как конечные разности используются при интерполяции, рассмотрим следующую таблицу:
Величины в первом столбце таблицы называются значениями аргумента, во втором - табличными значениями функции. В трех следующих столбцах приведены разности первого, второго и третьего порядков. Числа 7, 12, 6 называются "ведущими" или "диагональными разностями", соответствующими первому аргументу. Термин "диагональные" использован потому, что разности относительно соответствующих аргументов и табличных значений располагаются не по горизонтали. Величина (1/2) (19 + 37) = 28 называется центральной разностью, соответствующей третьему аргументу, и обозначается символом md. Греческая буква m означает среднее, md - среднее соседних разностей. Величина 18 называется центральной разностью второго порядка и обозначается символом d2 . Термин "центральная" указывает на то, что эти разности расположены по центру относительно аргумента, т.к. они либо лежат на одной горизонтали с аргументом, либо являются средними значений, расположенных по соседству с этой горизонталью. Обобщая, таблицу величин можно записать в символических обозначениях следующим образом:
Величины D f (x), D2 f (x), D3 f (x) представляют собой диагональные разности, соответствующие аргументу x. Если мы захотим найти табличные значения для аргумента x + pd, где p - некоторое произвольно выбранное число, то необходимо подставить соответствующие значения в следующий ряд, известный под названием интерполяционной формулы Грегори - Ньютона (в русскоязычной литературе эту формулу принято называть формулой Ньютона):
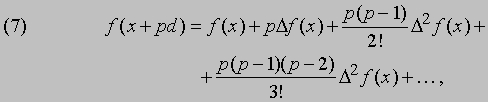
где 2! (читается "два факториал") означает 1*2, 3! = 1*2* 3 и т.д. В литературе встречается несколько вариантов формулы Грегори - Ньютона. В некоторых из них вместо диагональных разностей используются центральные разности. Так, центральные разности, соответствующие аргументу x, определяются следующим образом:
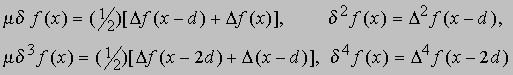
и т.д. В качестве примера найдем по формуле интерполяции значение (2,5)3 из приведенной выше числовой таблицы. Так как d = 1, p = 1/2 и диагональные разности, соответствующие x = 2, равны D = 19, D2 = 18, D3 = 6, находим по формуле интерполяции
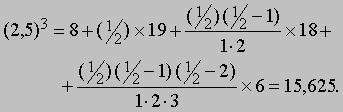
Символические методы. Один из наиболее удивительных аспектов исчисления конечных разностей связан с символическими (или операторными) методами. Чтобы понять их суть, рассмотрим символ E, называемый оператором и определяемый соотношением
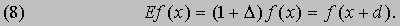
Пусть E 2f (x) - результат действия E на Ef (x), тогда E 2f (x) = f (x + 2d). Пользуясь математической индукцией, получаем для произвольного индекса p формулу
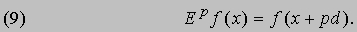
Опустим в формуле (8) символ функции и рассмотрим соотношение между одними лишь символами E = 1 + D. Оказалось, что с этим равенством и с другими, выводимыми из него, можно обращаться в соответствии с обычными правилами алгебры. Если степени символов интерпретировать как результат последовательного применения операторов Е и D, то полученные формулы также будут справедливы. Рассмотрим, например, Ep = (1 + D)p. Если правую часть равенства разложить по формуле бинома, а полученный ряд применить к f (x), мы получим разложение, стоящее в правой части интерполяционной формулы (7). Из (9) следует, что запись Epf (x) эквивалентна f (x + pd). Таким образом, биномиальное разложение, примененное к f (x) как операторное и приравненное к f (x + pd), дает формулу Грегори - Ньютона. Этот пример иллюстрирует характерные особенности символического (операторного) метода. Он позволил открыть так много замечательных формул, что большинство авторов, впервые его применивших, в своих работах не могли не выразить своего восхищения его мощью. Тайна эффективности этого метода кроется в том, что основной закон комбинирования алгебраических величин, с одной стороны, и операторы, такие, как D и Е, с другой, удовлетворяют правилу сложения показателей степеней
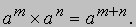
Следует иметь в виду, однако, что в первом случае символ произведения интерпретируется как обычное умножение, а во втором как последовательное выполнение операций. Символические методы позволяют установить связь исчисления конечных разностей с дифференциальным исчислением. Чтобы убедиться в этом, обозначим производную от f (x) символом Df (x), вторую производную - символом D 2f (x) и т.д. Разложение f (x + d) в ряд Тейлора (см. МАТЕМАТИЧЕСКИЙ АНАЛИЗ) можно записать символически в виде
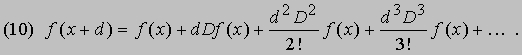
Учитывая, что разложение в ряд функции ez, где e = 2,71828ј - основание натуральных логарифмов, имеет вид
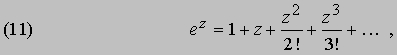
разложение (10) можно записать как
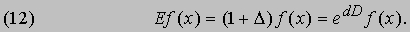
Опуская, как и прежде, символ функции, получаем чисто символическое уравнение

Если разрешить его относительно D по обычным правилам алгебры и принять во внимание разложение в ряд Тейлора для логарифмической функции, то получим
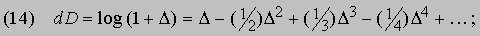
т.е.
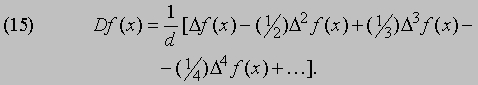
Еще более замечательные соотношения получаются для обратных операторов D-1 и D-1. Первый оператор интерпретируется как символ интегрирования т, а второй - как символ суммирования е, определяемый следующим образом:
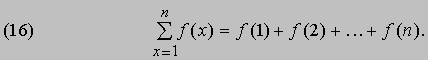
Хотя D-1 и D-1 следует рассматривать как символы операторов, примечательно, что над ними можно производить алгебраические операции так, как если бы это были величины 1/D и 1/D. В качестве примера применения символического метода решим уравнение (13) относительно 1/D:
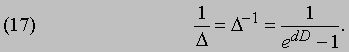
Для интерпретации этого соотношения необходимо иметь в виду разложение
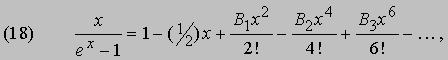
где B1 = 1/6, B2 = 1/30, B3 = 1/42 - т.н. числа Бернулли, названные так в честь открывшего их Я.Бернулли (1654-1705). Эти числа используются в различных разделах исчисления конечных разностей. Бернулли с гордостью заявлял, что с их помощью он нашел сумму десятых степеней первой тысячи натуральных чисел "за половину четверти часа". Подставив x вместо dD в правой части разложения (18) и сделав небольшие преобразования, можно записать (17) в виде
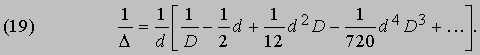
Вспомнив, что означали эти символы, и применив формулу к f (x), получим следующее разложение:
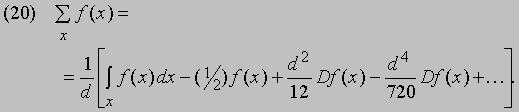
Суммирование рядов. Метод конечных разностей особенно удобен при суммировании рядов. Чтобы убедиться в этом, предположим, что в (1) d = 1, и рассмотрим сумму
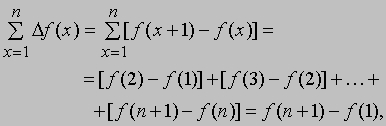
которую можно записать в более компактном виде
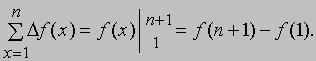
Заметим, что
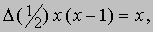
откуда
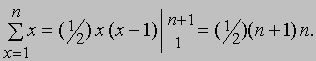
Тот же результат можно получить и из формулы (20). В этом случае, полагая d = 1 и f (x) = x, получаем
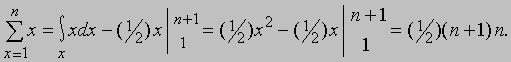
Разностные уравнения. В некоторых приложениях метода конечных разностей встречаются уравнения, типичными примерами которых являются следующие:
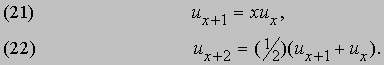
Такие уравнения называются "разностными уравнениями", так как их можно превратить в соотношения между разностями u. Например, первое уравнение можно записать в виде Dux = (x - 1)ux, а второе - в виде D2ux + 3/2 Dux = 0. Первое называется разностным уравнением первого порядка, второе - второго порядка. Такие уравнения встречаются, в частности, в приложениях теории вероятностей, для нахождения последовательных значений величины ux, когда x пробегает некоторую последовательность целых чисел. Такие образом, для уравнения (21), если u1 =1 и x = 2, 3, 4, ј, n, получаем
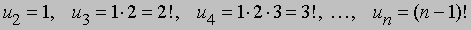
Аналогично, для (22), если u0 = 1, u1 = 0 и x = 2, 3, 4, ј, n, мы получаем следующую последовательность значений:
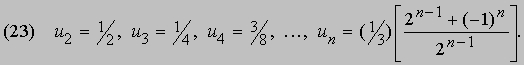
В общем случае разностные уравнения имеют также решения, определяемые в непрерывной области значений x. Например, частным решением уравнения (21) является "гамма-функция" G (x), так как одно из фундаментальных свойств этой функции состоит в том, что G (x + 1) = xG (x) (см. ФУНКЦИЯ). Такое решение мы получим из уравнения (22), положив ux = mx. Подставляя эту функцию в (22), мы получаем уравнение
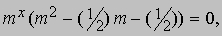
откуда m = 1, m = -1/2. Следовательно, уравнение (22) имеет решение

где А и В - произвольные постоянные. В частности, для A = 1/3 и B = 2/3 мы получим при целочисленных значениях x последовательность (23). Но (24) - не самое общее решение уравнения (22), так как другое решение можно получить, умножив любое частное решение на g (x), где g (x) - произвольная функция единичного периода, т.е. удовлетворяет уравнению
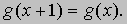
Примерами таких функций могут служить sin2px, cos2px, sin6px, cos6px и т.д. Подставляя в (22)
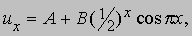
нетрудно убедиться в том, что ux - решение уравнения (22). Это решение получено при умножении второго члена в правой части (24) на подходящим образом выбранную функцию единичного периода.