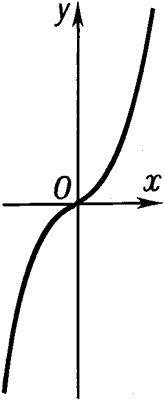
Куби́ческая пара́бола - алгебраическая кривая 3-го порядка: у = х³.

* * *

КУБИЧЕСКАЯ ПАРАБОЛА - КУБИ́ЧЕСКАЯ ПАРА́БОЛА, алгебраическая кривая 3-го порядка: y = x³ .

КУБИЧЕСКАЯ ПАРАБОЛА - алгебраическая кривая 3-го порядка: y = x3 .

Составить слова из слова кубическая парабола

Куби́ческая сингони́я - кристаллографическая сингония, для которой характерно соотношение между углами и рёбрами элементарной ячейки кристалла: а = b = с, α = β = γ = 90º. Подразделяется на 5 классов (точечных групп симметрии).

* * *

КУБИЧЕСКАЯ СИНГОНИЯ - КУБИ́ЧЕСКАЯ СИНГОНИ́Я, кристаллографическая сингония (см. СИНГОНИЯ), для которой характерно соотношение между углами и ребрами элементарной ячейки кристалла (см. ЭЛЕМЕНТАРНАЯ ЯЧЕЙКА КРИСТАЛЛА): a=b=c, a=b=g=90 °. Подразделяется на 5 классов (точечных групп симметрии (см. ТОЧЕЧНАЯ ГРУППА СИММЕТРИИ)). Это единственная сингония, симметрии которой отвечает обычная декартова система координат, элементарная ячейка - куб. У кристаллов кубической сингонии обязательно есть четыре оси 3 (третьего порядка), расположенные как пространственные диагонали куба.

КУБИЧЕСКАЯ сингония - кристаллографическая сингония, для которой характерно соотношение между углами и ребрами элементарной ячейки кристалла: a=b=c, ??????90 .. Подразделяется на 5 классов (точечных групп симметрии).

Составить слова из слова кубическая сингония

I прил.

1. соотн. с сущ. куб I, связанный с ним

2. Свойственный кубу [куб I], характерный для него.

3. Имеющий форму куба [куб I 1.].

II прил.

соотн. с сущ. куб II, связанный с ним

КУБИ́ЧЕСКИЙ, кубическая, кубическое.

1. прил. к куб¹ в 1 и 4 знач. (мат.). Кубическая форма. Кубическая степень. Извлечь кубический корень.

2. Выраженный в мерах, за единицу объема которых принят куб. Кубическая система мер. Кубический метр. Кубическая единица (куб, служащий единицей измерения).

КУБИ́ЧЕСКИЙ, -ая, -ое. Относящийся к единицам измерения объёма. К. метр.

КУБИ́ЧЕСКИЙ см. 1. Куб.

-ая, -ое.

1. Имеющий форму куба¹ (в 1 знач.).

Кубическое здание.

2. мат.

прил. к куб (в 3 знач.).

Кубический корень.

куби́ческий

куби́ческий

куби́ческий, куби́ческая, куби́ческое, куби́ческие, куби́ческого, куби́ческой, куби́ческих, куби́ческому, куби́ческим, куби́ческую, куби́ческою, куби́ческими, куби́ческом, куби́ческ, куби́ческа, куби́ческо, куби́чески

прил., кол-во синонимов: 1

Syn: кубичный

куб/и́ческ/ий.

куби́ческий п 3a✕~

КУБИЧЕСКИЙ, КУБИЧНЫЙ ая, ое. cubique adj. <, лат. cubicus.

1. Имеющий форму куба. шестигранника. Сл. 18. Большая голова кубической фигуры. С.-Меран 20. Горница имела совершенно кубический вид. ТВЭО 50 14.

2. Связанный с объемом, измерением тела. Сл. 18. Кубичной, что имеет широту, длину и глубину. ФРЛ-1 2 528. Лес, каменья и иные товары, которые могут приводиться в кубические футы, не должни быть меряемы иным образом. УВМ 395.

3. мат. Правила кубичнаго деления. Кург. Арифм. 206. Арифметика .. Корень квадратный и Кубический извлекает. Тред. СП 2 254. // Сл. 18. Извлечь кубический корень. Кубическое уравнение. БАС-1. - Лекс. Нордстет 1780: куби/ческий; Сл. 18: куби/ческий 1703, куби/чный 1703.

КУБИЧЕСКИЙ (от слова куб). 1) имеющий вид куба. 2) мера, имеющая форму куба, т. е. правильного шестигранника. 3) корень, всякая величина, которая, будучи помножена три раза сама на себя, дает данную величину.

Составить слова из слова кубический

Куби́ческое уравне́ние - алгебраическое уравнение 3-й степени: ах³ + bx² + сх + d = 0, где а ≠ 0. Решение кубического уравнения (после замены х = у - b/3а) может быть найдено по так называемой формуле Кардано.

* * *

КУБИЧЕСКОЕ УРАВНЕНИЕ - КУБИ́ЧЕСКОЕ УРАВНЕ́НИЕ, алгебраическое уравнение 3-й степени: ax³+bx²+cx+d = 0, где a№0. Решение кубического уравнения (после замены x=y-b/3 a) может быть найдено по т. н. формуле Кардано (см. КАРДАНО Джероламо).

КУБИЧЕСКОЕ УРАВНЕНИЕ - алгебраическое уравнение 3-й степени: ax3+bx2+cx+d = 0, где a?0. Решение кубического уравнения (после замены x=y-b/3 a) может быть найдено по т. н. формуле Кардано.

Составить слова из слова кубическое уравнение