Множа(йш)е - больше
множайший
Толковый словарь Ушакова
МНОЖА́ЙШИЙ, множащая, множащее (книжн, устар.). превосх. к многий.
Орфографический словарь
Полезные сервисы
множащий
Орфографический словарь
Синонимы к слову множащий
прил., кол-во синонимов: 9
наращивающий (11)
перемножающий (3)
повышающий (18)
поднимающий (80)
помножающий (3)
преумножающий (2)
приумножающий (10)
увеличивающий (26)
умножающий (10)
Полезные сервисы
множащийся
Орфографический словарь
Синонимы к слову множащийся
прил., кол-во синонимов: 11
возрастающий (18)
наращивающийся (10)
перемножающийся (3)
плодящийся (8)
повышающийся (24)
поднимающийся (101)
помножающийся (3)
размножающийся (13)
растущий (43)
увеличивающийся (48)
умножающийся (15)
Полезные сервисы
множенный
Орфографический словарь
Синонимы к слову множенный
Морфемно-орфографический словарь
Полезные сервисы
множеств теория
Энциклопедический словарь
Мно́жеств тео́рия - раздел математики, в котором изучаются общие свойства множеств, преимущественно бесконечных. Понятие множества - простейшее математическое понятие, оно не определяется, а лишь поясняется при помощи примеров: множество книг на полке, множество точек на прямой (точечное множество) и т. д. То, что данный предмет (элемент, точка) x принадлежит множеству M, записывают 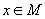 . Теория множеств лежит в основе многих математических дисциплин; она оказала глубокое влияние на понимание предмета самой математики. Об относящихся сюда понятиях см. Подмножество, Объединение множеств, Пересечение множеств, Пустое множество, Счётное множество, Континуум.
. Теория множеств лежит в основе многих математических дисциплин; она оказала глубокое влияние на понимание предмета самой математики. Об относящихся сюда понятиях см. Подмножество, Объединение множеств, Пересечение множеств, Пустое множество, Счётное множество, Континуум.
* * *
МНОЖЕСТВ ТЕОРИЯ - МНО́ЖЕСТВ ТЕО́РИЯ, раздел математики, в котором изучаются общие свойства множеств, преимущественно бесконечных. Понятие множества - простейшее математическое понятие, оно не определяется, а лишь поясняется при помощи примеров: множество книг на полке, множество точек на прямой (точечное множество) и т. д. То, что данный предмет (элемент, точка) х принадлежит множеству М, записывают х О М. М. т. лежит в основе многих математических дисциплин; она оказала глубокое влияние на понимание предмета самой математики. Об относящихся сюда понятиях см. Подмножество (см. ПОДМНОЖЕСТВО), Объединение множеств (см. ОБЪЕДИНЕНИЕ МНОЖЕСТВ), Пересечение множеств (см. ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ), Пустое множество (см. ПУСТОЕ МНОЖЕСТВО), Счетное множество (см. СЧЕТНОЕ МНОЖЕСТВО), Континуум (см. КОНТИНУУМ).
Большой энциклопедический словарь
МНОЖЕСТВ ТЕОРИЯ - раздел математики, в котором изучаются общие свойства множеств, преимущественно бесконечных. понятие множества - простейшее математическое понятие, оно не определяется, а лишь поясняется при помощи примеров: множество книг на полке, множество точек на прямой (точечное множество) и т. д. То, что данный предмет (элемент, точка) х принадлежит множеству М, записывают х О М. М. т. лежит в основе многих математических дисциплин; она оказала глубокое влияние на понимание предмета самой математики. Об относящихся сюда понятиях см. Подмножество, Объединение множеств, Пересечение множеств, Пустое множество, Счетное множество, Континуум.
Энциклопедия Кольера
Под множеством понимается совокупность каких-либо объектов, называемых элементами множества. Теория множеств занимается изучением свойств как произвольных множеств, так и множеств специального вида независимо от природы образующих их элементов. Терминология и многие результаты этой теории широко используются в математике, например в математическом анализе, геометрии и теории вероятностей.
Терминология. Если каждый элемент множества B является элементом множества A, то множество B называется подмножеством множества A. Например, если множество A состоит из чисел 1, 2 и 3, то у него существует 8 подмножеств (три из них содержат по 1 элементу, три - содержат по 2 элемента, одно подмножество, по определению, есть само множество A и восьмое подмножество - это пустое множество, не содержащее ни одного элемента). Запись x О A означает, что x - элемент множества A, а B М A - что B является подмножеством множества A. Если универсальное множество, из которого мы берем элементы всех множеств, обозначить через I, то элементы, принадлежащие I, но не входящие в A, образуют множество, называемое дополнением множества A и обозначаемое C(A) или A'. Множество, не содержащее ни одного элемента, называется пустым множеством. Над множествами можно производить операции, напоминающие операции, производимые в арифметике над числами. Объединением AB множеств A и B называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств A и B (элемент, принадлежащий множествам A и B одновременно засчитывается при включении в AB только один раз). Пересечением AB множеств A и B называется множество, состоящее из всех элементов, принадлежащих как A, так и B. Предположим, например, что множество I состоит из всех букв русского алфавита, A - из всех согласных, а множество B - из букв, встречающихся в слове "энциклопедия". Тогда объединение AB состоит из всех букв алфавита, кроме а, е, у, ъ, ь, ы, ю, пересечение AB - из букв д, к, л, н, п, ц, а дополнение C(A) - из всех гласных. Раздел теории множеств, который занимается исследованием операций над множествами, называется алгеброй множеств. Пустое множество играет в алгебре множеств роль нуля, и поэтому его часто обозначают символом О; например, AO = A, AO = O. Булева алгебра. Алгебра множеств является подразделом булевых алгебр, впервые возникших в трудах Дж. Буля (1815-1864). В аксиомах булевой алгебры отражена аналогия между понятиями "множества", "событие" и "высказывания". Логические высказывания можно записать с помощью множеств и проанализировать с помощью булевой алгебры. Даже не вдаваясь в детальное изучение законов булевой алгебры, мы можем получить представление о том, как она используется на примере одной из логических задач Льюиса Кэрролла. Пусть у нас имеется некоторый набор утверждений: 1. Не бывает котенка, который любит рыбу и которого нельзя научить всяким забавным штукам; 2. Не бывает котенка без хвоста, который будет играть с гориллой; 3. Котята с усами всегда любят рыбу; 4. Не бывает котенка с зелеными глазами, которого можно научить забавным штукам; 5. Не бывает котят с хвостами, но без усов. Какое заключение можно вывести из этих утверждений? Рассмотрим следующие множества (универсальное множество I включает в себя всех котят): A - котята, любящие рыбу; B - котята, обучаемые забавным штукам; D - котята с хвостами; E - котята, которые будут играть с гориллой; F - котята с зелеными глазами и G - котята с усами. Первое утверждение гласит, что множество котят, которые любят рыбу, и дополнение множества котят, обучаемых забавным штукам, не имеют общих элементов. Символически это записывается как 1. AC(B) = O. Аналогичным образом остальные утверждения можно записать так: 2. C(D)E = O; 3. G М A; 4. BF = O; 5. D М G. Принимая во внимание теоретико-множественный смысл символов (или воспользовавшись законами булевой алгебры), мы можем переписать утверждения 1, 2 и 4 в виде 1. A М B; 2. E М D; 4. B М C(F). Таким образом, мы переформулировали исходные утверждения в следующие: 1. Котят, которые любят рыбу, можно обучить забавным штукам; 2. У котят, которые будут играть с гориллой, есть хвосты; 4. У котят, которых можно обучить забавным штукам, глаза не зеленые; Теперь можно расположить символические записи утверждений в таком порядке, чтобы последний символ предыдущего утверждения совпадал с первым символом следующего (этому условию удовлетворяет расположение утверждений в порядке 2, 5, 3, 1, 4). Возникает цепочка включений E М D М G М A М B М C(F), из которой можно сделать вывод, что E М C(F) или "Не бывает котенка с зелеными глазами, который будет играть с гориллой". Такое заключение едва ли очевидно, если рассматривать пять исходных утверждений в их словесной формулировке.
Сравнение множеств. Если из элементов двух множеств можно составить пары таким образом, чтобы каждому элементу первого множества соответствовал определенный элемент второго множества, а каждому элементу второго множества соответствовал один и только один элемент первого множества, то говорят, что между такими двумя множествами установлено взаимно однозначное соответствие. Чтобы установить взаимно однозначное соответствие, необязательно пересчитывать элементы множеств. Например, мы знаем, что американские штаты находятся во взаимно однозначном соответствии с их столицами, хотя можем оставаться в неведении относительно общего их числа. Мы могли бы утверждать: "Столиц штатов ровно столько, сколько штатов". Между двумя конечными множествами можно установить взаимно однозначное соответствие тогда и только тогда, когда оба множества состоят из одного и того же числа элементов. В теории множеств аналогичные утверждения используются, даже когда множества содержат бесконечно много элементов. Если между двумя множествами можно установить взаимно однозначное соответствие, то говорят, что они имеют одинаковое количество элементов или равномощны. Если же при любом способе образования пар некоторые элементы из первого множества остаются без пары, то говорят, что первое множество содержит больше элементов, чем второе, или, что первое множество имеет большую мощность. С понятием мощности связаны, казалось бы, удивительные результаты. Например, на первый взгляд положительных целых чисел в два раза больше, чем четных положительных чисел, так как четно каждое второе число. Но, согласно теории множеств, четных положительных чисел столько же, сколько всех положительных целых чисел. Действительно, можно образовать пары чисел 2 и 1, 4 и 2, 6 и 3 и, вообще каждому четному числу 2n поставить в соответствие целое число n. Именно это обстоятельство имел в виду Б. Рассел (1872-1970), сформулировав факт, названный им парадоксом Тристрама Шенди. Герой романа Стерна сетовал на то, что ему потребовался целый год, чтобы изложить события первого дня его жизни, еще один год понадобился, чтобы описать второй день, и что при таком темпе он никогда не завершит свое жизнеописание. Рассел возразил, заметив, что если бы Тристрам Шенди жил вечно, то смог бы закончить свое жизнеописание, так как события n-го дня Шенди мог бы описать за n-й год и, таким образом, в летописи его жизни ни один день не остался бы не запечатленным. Иначе говоря, если бы жизнь длилась бесконечно, то она насчитывала бы столько же лет, сколько дней. Эти примеры показывают, что бесконечное множество можно поставить во взаимно однозначное соответствие со своим бесконечным подмножеством. Иногда это свойство принимают за определение бесконечного. Если можно установить взаимно однозначное соответствие между некоторым множеством и множеством положительных целых чисел, то говорят, что такое множество счетно. Для обозначения количества элементов в счетном множестве часто используют символ А0 (алеф-нуль). Так называемые "трансфинитные" числа, например А0, могут не подчиняться обычным законам арифметики. Например, так как существует А0 четных чисел, А0 нечетных и А0 целых чисел, то приходится признать, что А0 + А0 = А0. Идея сравнения множеств путем установления взаимно однозначного соответствия между ними используется в различных разделах математики. Число всех действительных чисел, как показал основатель научной теории множеств Г. Кантор (1845-1918), больше, чем А0 чисел. Следовательно, если можно показать, что множество действительных чисел, обладающих некоторым особым свойством, является всего лишь счетным множеством, то заведомо должны существовать действительные числа, этим свойством не обладающие. Например, так как множество алгебраических чисел счетно, должны существовать неалгебраические числа. Такие числа называются трансцендентными. Поразительная и далеко не очевидная теорема, высказанная в качестве гипотезы Кантором и доказанная Э. Шредером и Ф. Бернштейном около 1896, утверждает, что если можно установить взаимно однозначное соответствие между множеством A и подмножеством множества B, и между множеством B и подмножеством множества A, то существует взаимно однозначное соответствие между всем множеством A и всем множеством B.
Парадоксы. Мы уже упоминали о том, что в теории множеств встречаются такие утверждения, как парадокс Тристрама Шенди, которые выглядят противоречащими здравому смыслу. Эти парадоксы возникают просто потому, что теория множеств, подобно многим математическим и физическим теориям, облекает свои идеи в обычные слова, вкладывая в них особый смысл. Однако существуют и парадоксы, возникающие из-за внутренних логических трудностей самой теории множеств. Обильным источником парадоксов такого типа служит широко распространенная практика задания множества путем указания некоторого свойства его элементов, например, "множество, состоящее из английских слов, содержащих менее 19 букв". Некритическое использование такого рода определений может привести к трудностям. Например, некоторые статьи в этой энциклопедии содержат ссылки на себя, другие таких ссылок не содержат. Мы могли бы включить в нашу энциклопедию дополнительную статью, состоящую только из перечня статей, не содержащих ссылок на себя. Принадлежала бы такая статья множеству статей, не содержащих ссылок на себя, или не принадлежала бы? Любой ответ противоречил бы отличительному свойству, которым по их определению наделены элементы множества. Это - одна из форм так называемого парадокса Рассела, названного в честь своего автора Бертрана Рассела. "Множество всех множеств" - еще одно понятие, также приводящее к парадоксу. Существование парадоксов показывает, с какой осторожностью следует пользоваться терминологией теории множеств. Тем не менее теория множеств настолько полезна, что большинство математиков не хотели бы отказываться от нее. Было затрачено много усилий, чтобы развить методы, позволяющие исключить возникновение парадоксов в теории множеств. В приложениях теории множеств к другим разделам математики универсальное множество I обычно само является некоторым определенным множеством и парадоксальные ситуации здесь не возникают.
Аксиома выбора. Неожиданные трудности в теории множеств могут возникнуть, казалось бы, в самых простых случаях. Если, например, задано семейство непересекающихся множеств, ни одно из которых не пусто, то интуитивно кажется очевидным, что мы можем построить новое множество, содержащее ровно по одному элементу из каждого множества, входящего в это семейство. Но если наше семейство содержит бесконечно много множеств, то для построения нового множества может потребоваться бесконечное число произвольных выборов, а законность такого процесса при тщательном анализе становится отнюдь не очевидной. Аксиома выбора, утверждающая, что такое множество существует, была впервые сформулирована в 1904 Э. Цермело (1871-1953). До сих пор не удалось показать, что аксиома выбора следует из остальных аксиом теории множеств. Но около 1938 К.Гедель (1906-1978) показал, что если теория множеств непротиворечива (т.е. не содержит внутренних противоречий) без аксиомы выбора, то она остается непротиворечивой и после присоединения к ней аксиомы выбора.
См. также
ЛИТЕРАТУРА
Куратовский К., Мостовский А. Теория множеств. М., 1970
Полезные сервисы
множественное описание
Практический толковый словарь
нлп Процесс описания одного и того же явления с различных позиций восприятия. (Смотри также:Позиция восприятия).
Полезные сервисы
множественное число
Толковый словарь Ожегова
МНО́ЖЕСТВЕННЫЙ, -ая, -ое; -вен, -венна (книжн.). Существующий во множестве, проявляющийся во множестве форм, видов.
Лингвистические термины
множественное число - см. число множественное (в статье число грамматическое).
Пятиязычный словарь лингвистических терминов
См. plurale.
Полезные сервисы
множественное число ассоциативное
множественное число ассоциативное (репрезентативное, аппроксимативное)
множественное число видовое
Лингвистические термины
Значение граммемы множественного числа, обозначающее разные виды или разные манифестации названий веществ и их свойств: кислоты, хвои, соки.
Морфология
Значение граммемы множественного числа, обозначающее разные виды или разные манифестации названий веществ и их свойств: кислоты, хвои, соки.
Полезные сервисы
множественное число неопределенное
Лингвистические термины
Значение граммемы множественного числа, обозначающее количественно не охарактеризованный предмет: В купе новые пассажиры - мужчина в очках.
Морфология
Значение граммемы множественного числа, обозначающее количественно не охарактеризованный предмет: В купе новые пассажиры - мужчина в очках.
Полезные сервисы
множественное число родовое
множественное число существительных
Лингвистические термины
Грамматическая категория сущ., употребляемая в художественной речи чаще всего в конкретном значении, указывающая на совокупность, множество отдельных считаемых предметов: По небу бродили обрывки туч, пышные, странных очертаний и красок. Между ними ласково блестели темно-голубые клочки неба, украшенные золотыми крапинками звезд.
Полезные сервисы
множественное число эмфатическое
множественность
Толковый словарь
Толковый словарь Ушакова
МНО́ЖЕСТВЕННОСТЬ, множественности, мн. нет, жен. (книжн.). отвлеч. сущ. к множественный. Множественность форм.
Толковый словарь Ожегова
МНО́ЖЕСТВЕННЫЙ, -ая, -ое; -вен, -венна (книжн.). Существующий во множестве, проявляющийся во множестве форм, видов.
Академический словарь
Орфографический словарь
Формы слов для слова множественность
мно́жественность, мно́жественности, мно́жественностей, мно́жественностям, мно́жественностью, мно́жественностями, мно́жественностях
Синонимы к слову множественность
Антонимы к слову множественность
Грамматический словарь
Полезные сервисы
множественный
Толковый словарь
Толковый словарь Ушакова
МНО́ЖЕСТВЕННЫЙ, множественная, множественное (книжн.). Относящийся к множеству (в 1 знач.), существующий во множестве, в большом числе.
• Множественное число (грам.) - форма склонения и спряжения, употр., когда речь идет о многих лицах или предметах.
Толковый словарь Ожегова
МНО́ЖЕСТВЕННЫЙ, -ая, -ое; -вен, -венна (книжн.). Существующий во множестве, проявляющийся во множестве форм, видов.
Множественное число грамматическая категория, обозначающая, что предмет представлен в количестве, большем, чем один. Имя существительное в форме множественного числа. Глагол в прошедшем времени в форме множественного числа.
| сущ. множественность, -и, жен.
Энциклопедический словарь
МНО́ЖЕСТВЕННЫЙ -ая, -ое; -вен, -венна, -венно. Состоящий из множества чего-л.; существующий во множестве, проявляющийся во множестве форм, видов. М-ые следы. Предпринимать м-ые попытки. Получать м-ые указания. М-ое число (лингв.; формы склонения и спряжения, употребляемые, когда речь идёт о двух или более лицах или предметах).
◁ Мно́жественность, -и; ж. М. видов растений.
Академический словарь
-ая, -ое; -вен, -венна, -венно.
Состоящий из множества чего-л.; существующий во множестве, проявляющийся во множестве форм, видов.
За обедом оба доктора говорили о том ---, что множественные невриты в последнее время наблюдаются очень часто. Чехов, Попрыгунья.
Множественный след гусениц сводил с дороги влево, во мглу горелой сосновой рощи. Леонов, Взятие Великошумска.
◊
множественное число
грамм.
формы склонения и спряжения, употребляемые, когда речь идет о двух или более лицах или предметах.
Орфографический словарь
Формы слов для слова множественный
мно́жественный, мно́жественная, мно́жественное, мно́жественные, мно́жественного, мно́жественной, мно́жественных, мно́жественному, мно́жественным, мно́жественную, мно́жественною, мно́жественными, мно́жественном, мно́жественен, мно́жествен, мно́жественна, мно́жественно, мно́жественны
Синонимы к слову множественный
Тезаурус русской деловой лексики
Идеография
↑ в виде, совокупность
множественный - существующий в виде совокупности (# число. # перелом).
множественность - численность в несколько единиц.
много.
многосторонний.
поли. . (политехнический).
мульти. . (мультидоступ).
множественное число.
составить.
счетверить.
▼ два, три, множество, люди, некоторый
↓ отношение, КОЛИЧЕСТВО, повторный, или (только)
Морфемно-орфографический словарь
Грамматический словарь
Полезные сервисы
множественный выбор
Методические термины
МНО́ЖЕСТВЕННЫЙ ВЫ́БОР (англ. multiple choice).
Выбор варианта ответа из некоторого предлагаемого множества (состоящего из правильного ответа и неправильных, или дистракторов). Распространенная форма составления тестовых заданий. Оптимальным считается выбор из четырех элементов. М. в. называют также заданием в закрытой форме, потому что учащийся не формулирует ответ самостоятельно, а выбирает один из предложенных вариантов. М. в. обычно предполагает стандартизированные формулировки задания и используется чаще всего на начальных стадиях отработки языкового материала. В отличие от заданий в открытой форме М. в. проверяет только одну сторону языковой компетенции: знание конкретной единицы, но не сформированность умения пользоваться ею. См. также тестовое задание.
Полезные сервисы
множество
Толковый словарь
I ср.
Употребляется как неопределённо-количественное слово; очень много кого-либо, очень большое число чего-либо.
II ср.
Совокупность элементов, выделенных по какому-либо признаку в обособленную группу (в математике).
МНО́ЖЕСТВО - сущ., с., употр. часто
Морфология: (нет) чего? мно́жества, чему? мно́жеству, (вижу) что? мно́жество, чем? мно́жеством, о чём? о мно́жестве; мн. что? мно́жества, (нет) чего? мно́жеств, чему? мно́жествам, (вижу) что? мно́жества, чем? мно́жествами, о чём? о мно́жествах
1. Множеством называют очень большое количество кого-либо или чего-либо.
В результате кризиса потеряло работу множество людей. | О ней написано множество статей. | Современная косметология знает множество способов ухода за кожей лица.
2. В математике и информатике множеством называют группу однородных объектов.
Толковый словарь Ушакова
МНО́ЖЕСТВО, множества, ср. (книжн.).
1. только ед. Неопределенно большое количество, число чего-нибудь. Множество рабочих. Множество фактов. «Я слышал в жизни множество отличнейших певцов.» Некрасов.
2. Совокупность элементов, выделенных в обособленную группу по какому-нибудь признаку (мат.). Конечное, бесконечное множество. Эквивалентные множества.
Толковый словарь Ожегова
МНО́ЖЕСТВО, -а, ср.
1. Очень большое количество, число кого-чего-н. М. людей. М. случаев. Всяких запасов во множестве.
2. В математике: совокупность элементов, объединённых по какому-н. признаку. Теория множеств.
Толковый словарь Даля
Словарь существительных
МНО́ЖЕСТВО1́, -а, ср
Очень большое количество, число кого-, чего-л.;
Син.: обилие, масса.
Множество голосов.
МНО́ЖЕСТВО2́, -а, ср
Очень большое количество, число кого-, чего-л.
Александр с радостным трепетом прислушивался к одобрительному суду друзей, которых у него было множество и на службе, и по кондитерским, и в частных домах (Гонч.).
Энциклопедический словарь
МНО́ЖЕСТВО -а; ср.
1. Очень большое количество, число кого-, чего-л. М. народа. М. фактов. Вырастить м. цветов. Доказательства представлены во множестве. Великое м. примеров (очень много).
2. Матем. Совокупность элементов, объединённых по какому-л. признаку. Теория множеств. Счётное м.
* * *
мно́жество (матем.), см. Множеств теория.
* * *
МНОЖЕСТВО - МНО́ЖЕСТВО, в математике, см. Множеств теория (см. МНОЖЕСТВ ТЕОРИЯ).
Большой энциклопедический словарь
МНОЖЕСТВО - в математике, см. Множеств теория.
Академический словарь
-а, ср.
1. Очень большое количество, число кого-, чего-л.
Приближаясь [к дому], увидел он множество народа; крестьяне и дворовые люди толпились на барском дворе. Пушкин, Дубровский.
Шли распоряжения и насчет домашних запасов, которые, в виде варенья, соленья, сушенья и квашенья, производились во множестве. Салтыков-Щедрин, Убежище Монрепо.
Комнаты были заставлены таким множеством вазонов с цветами, ящиков с рассадой ---, что казалось, в квартире столько же зелени, сколько и в саду. Паустовский, Повесть о лесах.
2. мат.
Совокупность элементов, объединенных по какому-л. признаку.
Теория множеств.
◊
- великое множество
Поговорки
Орфографический словарь
Формы слов для слова множество
мно́жество, мно́жества, мно́жеств, мно́жеству, мно́жествам, мно́жеством, мно́жествами, мно́жестве, мно́жествах
Синонимы к слову множество
сущ., кол-во синонимов: 88
арава (2)
армада (6)
армия (46)
арсенал (10)
батарея (12)
без счета (53)
без счету (38)
без числа (50)
бездна (41)
бесчисленность (16)
более чем достаточно (42)
большое количество (44)
большое число (24)
в избытке (65)
вагон (96)
великое множество (15)
воз (26)
ворох (21)
гибель (49)
гора (76)
град (16)
груда (19)
избыток (22)
изобилие (42)
каскад (20)
кипа (24)
кодла (18)
кодло (21)
континуум (7)
короб (28)
косяк (31)
куча (50)
лавина (31)
легион (25)
лес (165)
лик (17)
масса (96)
миллионы (7)
мириады (21)
много (196)
многое множество (8)
множественность (5)
море (51)
навал (8)
немало (107)
несметное количество (33)
несметное число (25)
обилие (40)
огромное количество (33)
огромное число (22)
озев (5)
палестина (9)
подмножество (1)
полк (30)
полно (136)
полчище (26)
поток (55)
предостаточно (58)
премножество (9)
пропасть (48)
прорва (38)
пучок (26)
раздолье (17)
разливанное море (8)
разнообразие (15)
рой (36)
сборище (40)
сила (117)
силища (3)
сколько душе угодно (50)
сколько угодно (64)
сколько хочешь (59)
скопище (13)
сонм (9)
сонмище (7)
стая (35)
строй (48)
табун (26)
туча (29)
тьма (57)
тьма тем (17)
тьма-тьмущая (38)
уйма (41)
уймище (23)
хор (30)
целый короб (17)
целый ряд (28)
чертова гибель (10)
большое (или огромное, несметное и т. п.) количество, великое множество, обилие, изобилие, море, масса, мириады, поток, каскад, лавина, град; уйма, тьма, тьма-тьмущая, бездна, пропасть, разливанное море (разг.)
/ исчисляемых сущ.: большое (или огромное, несметное и т. п.) число, миллионы; уймища, прорва, (чёртова) гибель (прост.); многое множество, премножество, тьма тем (устар.)
/ предметов: целый ряд, гора, воз, вагон, груда, куча, кипа, ворох (разг.)
// однородных предметов: арсенал, батарея, армада (шутл.)
// высоких предметов: строй, лес
/ вестей, новостей: (целый) короб (разг.)
/ живых существ: стая, рой, туча, полчище; табун (разг. неодобр.)
// людей: полк, армия; легион (разг.); кодла (разг. неодобр.); сонм (высок.)
см. также много
сущ.
масса
уймища
бездна
пропасть
тьма
тьма-тьмущая
тьма тем
куча
воз
вагон
прорва
гибель
сила
море
гора
МНОЖЕСТВО
МНОЖЕСТВО, изобилие, лавина, море, обилие, поток, разг. бездна, разг. вагон, разг. воз, разг. куча, разг. масса, разг. пропасть, разг. тьма, разг. уйма, разг. уймища, разг.-сниж. гибель, разг.-сниж. прорва, разг.-сниж. сила, разг.-сниж. тьма-тьмущая
Тезаурус русской деловой лексики
Идиоматика
Идеография
▲ , совокупность
множество - совокупность объектов, имеющих к-л. общую характеристику;
однородная совокупность; совокупность видов;
неупорядоченная совокупность однородных попарно различных элементов;
оно включает все такие элементы; если не все, то это подмножество.
каждое множество может быть элементом другого множества; множество - вид классов (матем).
класс - не может быть элементом другого класса или множества (матем).
гнездо (# слов).
спектр, в физике - совокупность всех характеристических значений физической величины.
сборище.
подбор (# кушаний). | выбор (# товаров).
арсенал (# средств).
сортамент, сортимент. | созвездие (# талантов).
круг (# друзей. # действующих лиц. # вопросов. # обязанностей).
круги (официальные #. # интеллигенции).
он и ему подобные. среди себе подобных.
из того же ряда.
букет.
сборник. свод.
ансамбль. хор. | ассорти.
контингент.
сводка.
собирательные понятия - обозначают множество однородных предметов (толпа. библиотека).
▼ систематическая категория, химический элемент
сообщество животных, алфавит, собрание (предметов)
↓ который, когда-л. умножение, численность
общий, классификация, выбор, согласованный, перечень
Морфемно-орфографический словарь
Грамматический словарь
Сканворды для слова множество
- Неисчислимая «туча».
- Совокупность элементов, объединённых по какому-либо признаку.
- Мириады звёзд.
- ... Мандельброта.
Полезные сервисы
множивший
Синонимы к слову множивший
прил., кол-во синонимов: 10
наращивавший (12)
перемножавший (4)
повышавший (29)
поднимавший (124)
помножавший (4)
преумножавший (4)
приумножавший (9)
увеличивавший (25)
умножавший (14)
Полезные сервисы
множившийся
Синонимы к слову множившийся
прил., кол-во синонимов: 12
возраставший (26)
наращивавшийся (10)
перемножавшийся (4)
плодившийся (12)
повышавшийся (32)
поднимавшийся (133)
помножавшийся (4)
размножавшийся (18)
росший (61)
увеличивавшийся (65)
умножавшийся (18)
Полезные сервисы
множимое
Толковый словарь
Толковый словарь Ушакова
Энциклопедический словарь
Академический словарь
Орфографический словарь
Морфемно-орфографический словарь
Грамматический словарь
Сканворды для слова множимое
Полезные сервисы
множимый
Синонимы к слову множимый
прил., кол-во синонимов: 9
наращиваемый (10)
перемножаемый (3)
повышаемый (17)
поднимаемый (58)
помножаемый (3)
преумножаемый (2)
приумножаемый (11)
увеличиваемый (21)
умножаемый (8)
умножаемый, поднимаемый, преумножаемый, наращиваемый, повышаемый, помножаемый, перемножаемый, приумножаемый, увеличиваемый
Морфемно-орфографический словарь
Полезные сервисы
множитель
Толковый словарь
I м.
Второе из двух перемножаемых чисел или величин (в арифметике).
II м. разг.
Аппарат, служащий для размножения рукописей, чертежей и т.п. в каком-либо количестве экземпляров.
Толковый словарь Ушакова
МНО́ЖИТЕЛЬ, множителя, муж. (мат.). В действии умножения - число, которое показывает, сколько раз нужно повторить слагаемым какое-нибудь другое число (множимое), чтобы получить произведение.
Энциклопедический словарь
МНО́ЖИТЕЛЬ -я; м. Матем. Второе из двух перемножаемых чисел или величин. Найти неизвестный м. в уравнении.