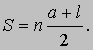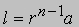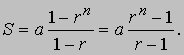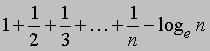I ж.
1. Ряд увеличивающихся или уменьшающихся чисел, в котором разность или отношение между соседними числами сохраняет постоянную величину (в математике).
2. разг.
Возрастание или уменьшение чего-либо (подобно арифметической или геометрической прогрессии).
II ж. устар.
Последовательное перемещение одноголосного или многоголосного музыкального построения в восходящем или нисходящем направлении; секвенция.
ПРОГРЕ́ССИЯ, прогрессии, жен. (лат. progressio - восхождение, приращение).
1. Ряд чисел, увеличивающихся или уменьшающихся так, что разность или отношение между каждыми двумя соседними числами сохраняет постоянную величину (мат.). Арифметическая, или разностная прогрессия. Геометрическая, или краткая прогрессия.
2. Повторение мотива в один или два такта в восходящем или нисходящем порядке, то же, что секвенция (муз. устар.).
ПРОГРЕ́ССИЯ, -и, жен. В математике: ряд увеличивающихся или уменьшающихся чисел, в к-ром разность или отношение между соседними числами сохраняет постоянную величину. Арифметическая п. Геометрическая п.
ПРОГРЕССИЯ - жен., лат., мат. лествица; ряд чисел, из которых каждое на столько же или во столько же раз более или менее предыдущего; первая прогрессия арифметическая, вторая геометрическая.
ПРОГРЕ́ССИЯ -и; ж. [от лат. progressio - движение вперёд] Матем. Ряд увеличивающихся или уменьшающихся чисел, в котором разность или отношение между соседними числами сохраняют постоянную величину. Арифметическая п. (последовательность чисел, каждое из которых получается из предыдущего путём прибавления или вычитания некоего постоянного числа). Геометрическая п. (последовательность чисел, каждое из которых получается из предыдущего путём умножения или деления на некое постоянное число). Возрастать в геометрической прогрессии. Уменьшаться в арифметической прогрессии.
* * *
прогре́ссия - см. Арифметическая прогрессия, Геометрическая прогрессия.
* * *
ПРОГРЕССИЯ - ПРОГРЕ́ССИЯ, см. Арифметическая прогрессия (см. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ), Геометрическая прогрессия (см. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ).
ПРОГРЕССИЯ - см. Арифметическая прогрессия, Геометрическая прогрессия.
-и, ж. мат.
Последовательный ряд чисел, из которых каждое получается из предыдущего прибавлением какого-л. постоянного числа (арифметическая прогрессия) или умножением на постоянное число (геометрическая прогрессия).
[От лат. progressio - движение вперед]
ПРОГРЕССИЯ - последовательность чисел, получаемых по некоторому правилу. Термин ныне во многом устарел и встречается только в сочетаниях "арифметическая прогрессия" и "геометрическая прогрессия". Арифметическая прогрессия - это последовательность чисел, в которой каждый член получается из предыдущего путем прибавления к нему одного и того же числа, называемого разностью этой арифметической прогрессии, например 1, 2, 3, 4, ј или 2, 5, 8, 11, 14, ј (многоточие означает "и т.д."). Разность между последовательными членами необязательно должна быть положительной, например, для прогрессии 3, 1, -1, -3, -5, ј она равна -2. Геометрическая прогрессия - это последовательность чисел, каждое из которых равно предыдущему, умноженному на некоторое постоянное для данной прогрессии число, называемое знаменателем прогрессии, например 5, 10, 20, 40, 80, ј или 5, -10, 20, -40, 80, ј (в первом случае знаменатель равен 2, во втором равен -2).
Формулы. Рассмотрим n членов арифметической прогрессии. Пусть a - первый член, l - последний член и d - разность между последовательными членами. Тогда l = a +(n - 1) d.
Сумма первых n членов прогрессии вычисляется следующим образом:
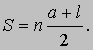
Эту формулу легко запомнить, суть ее в том, что сумма n членов равна числу членов, умноженному на полусумму первого и последнего членов. Например, сумма последовательных целых чисел от 1 до 50 равна (1/2)*50*51 = 1275. Рассмотрим теперь n членов геометрической прогрессии; пусть a - первый член, l - последний член, S - сумма первых n членов прогрессии. Вместо разности d мы теперь должны использовать знаменатель прогрессии r, равный отношению любого последующего члена к предыдущему. Тогда
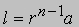
и
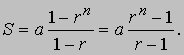
Например, если бы за первый день месяца вам заплатили 1 цент, а за каждый последующий день вы получали бы вдвое больше, чем за предыдущий, то за первые 10 дней вы заработали бы всего 10,23 долл., а за первые 30 дней уже 10737418,23 долл. Эти выкладки показывают, что при r >1 члены геометрической прогрессии в конце концов возрастают очень быстро. Такие геометрические прогрессии называются возрастающими. Они используются, например, при вычислении сложных процентов. Если 0 < r < 1, то геометрическая прогрессия называется убывающей, если r < 0, то прогрессия - знакочередующаяся. Если знаменатель прогрессии r заключен между -1 и +1, то величина rn при больших n очень мала, и при n (r) Ґ сумма стремится к пределу a/(1 - r), называемому суммой бесконечно убывающей геометрической прогрессии (см. также РЯДЫ). Если a и b - два заданных числа, то числа a, (a + b)/2 и b являются тремя последовательными членами арифметической прогрессии, а числа a, и b (a > 0, b > 0) - тремя последовательными членами геометрической прогрессии. Средние члены (a + b)/2 и называются соответственно средним арифметическим и средним геометрическим чисел a и b. (Арифметическое среднее совпадает с обычным средним.)
Другие прогрессии. Множество чисел иногда называется гармонической прогрессией, если величины, обратные этим числам, являются членами арифметической прогрессии. Например, числа 1, 1/2, 1/3, 1/4, ј образуют гармоническую прогрессию. Числа a, 2ab/(a + b) и b являются тремя последовательными членами гармонической прогрессии, а средний член называется гармоническим средним чисел a и b. Для суммы первых n членов гармонической прогрессии простой формулы не существует, но разность между суммой первых n членов и натуральным логарифмом числа n
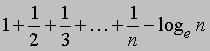
при n, стремящемся к бесконечности, стремится к некоторому пределу; этот предел называется постоянной Эйлера; ее приближенное значение равно 0,5772. В арифметической прогрессии разности между последовательными членами постоянны. Если разности не постоянны, а постоянны разности разностей, то прогрессия называется арифметической прогрессией второго порядка. Аналогичным образом определяются арифметические прогрессии более высоких порядков. Например, 2, 6, 12, 20, 30, ј - арифметическая прогрессия второго порядка, так как разности 4, 6, 8, 10, ј образуют арифметическую прогрессию с d = 2.
прогре́ссия, прогре́ссии, прогре́ссий, прогре́ссиям, прогре́ссию, прогре́ссией, прогре́ссиею, прогре́ссиями, прогре́ссиях
Syn: см. последовательность
прогрессия - в риторике: переход к новому; П. создает динамику речи и делает ее интересной, но разрывает связность речи.
ПРОГРЕССИЯ и, ж. prgression f. <, лат. progressio движение вперед, рост.
1. В математике - ряд увеличивающихся или уменьшающихся чисел, в котором разность или отношение между соседними величинами сохраняет постоянную величину. Арифметическая, геометрическая прогрессия. БАС-1. || О возрастании или уменьшении чего-л. подобно арифметической или геометрической прогрессии. БАС-1. Робость моя и конфузливость не ослабевают, а возрастают в чудовищной прогрессии. 15. 4. 1840. Белинский - В. П. Боткину. Каждое из обоих почтовых ведомств будет взимать за сии письма в свою пользу, по своим таксам и прогрессиям веса, свои внутренния весовыя деньги. 1843. ПСЗ-2 18 (1 561). Во всем видна прогрессия, И ныне на Руси Такое цветобесие, Что Боже упаси!! Соллогуб Букеты. // С. 3 439. При помощи переводов быстрота сообщения усиливается в огромной прогрессии. Бутовский 1847 1 130. Подчиняясь коридорной прогрессии, она <мадам Грицацуева> неслась со все усиливающейся быстротой. Ильф 12 стульев.
2. устар., спец. Последовательное перемещение одноголосного или многоголосного музыкального построения в восходящем или нисходящем направлении; секвенция. БАС-1. Фраза <Наташи из оперы "Русалка"> идет прогрессией из пронзительных диссонансов малой секунды. Серов Русалка. - Лекс. Ян. 1806: прогрессия; САН 1847: прогре/ссия.
ПРОГРЕССИЯ (лат. приращение; этим. см. прогрессивный. 1) ряд чисел или величин, увеличивающихся по известному закону. 2) в муз.: постепенное повторение мотива в 1 или 2 такта в восходящ. или нисходящем порядке.