ср.
1. процесс действия по гл. сопротивляться 1.
2. Свойство оказывать противодействие каким-либо воздействиям, изменениям.
3. Элемент электрической цепи, позволяющий регулировать силу тока в цепи.
ср.
1. процесс действия по гл. сопротивляться 1.
2. Свойство оказывать противодействие каким-либо воздействиям, изменениям.
3. Элемент электрической цепи, позволяющий регулировать силу тока в цепи.
СОПРОТИВЛЕ́НИЕ - сущ., с., употр. сравн. часто
Морфология: (нет) чего? сопротивле́ния, чему? сопротивле́нию, (вижу) что? сопротивле́ние, чем? сопротивле́нием, о чём? о сопротивле́нии
1. Сопротивлением называют чей-либо решительный отказ подчиняться кому-либо, чему-либо.
Попытка заставить учить уроки вызывает сопротивление ребёнка. | Требования повысить зарплату встречают сопротивление начальства.
2. Сопротивлением называют ответные вооружённые действия тех, на кого напал (нападает) враг.
Отчаянное сопротивление противника. | Оказать вооружённое сопротивление. | Подавить сопротивление гарнизона. | Прекратить сопротивление и сдаться.
3. Сопротивлением в странах Западной Европы называют народное движение против действий захватчиков в годы фашистской оккупации.
Участник Сопротивления. | В годы Сопротивления.
4. Если кто-либо предлагает пойти по линии (по пути) наименьшего сопротивле́ния, то это означает, что кто-либо предлагает кому-либо выбрать самый лёгкий способ решения чего-либо, рекомендует уклониться от трудностей, неприятностей.
5. Сопротивлением называют способность организма противостоять каким-либо внешним воздействиям, болезням.
Частые простуды понижают сопротивление организма к некоторым бактериям и вирусам.
6. Сопротивление материалов - это теоретическая дисциплина о прочности и видах деформации материалов и элементов машин и сооружений.
7. Сопротивлением называют свойство воды, воздуха препятствовать движению тела, объекта в воздушной, водной среде.
Волновое, гидравлическое сопротивление. | Сопротивление воздуха резко увеличивается. | Возросшее сопротивление встречного тока воды. | Поскольку плотность атмосферы быстро падает с высотой, основное сопротивление спутник испытывает вблизи перигея.
8. Электрическое сопротивление - это свойство проводника препятствовать движению электрического тока.
Контактное, переходное, входное сопротивление. | Внутреннее сопротивление батареи может ограничивать необходимый ток.
СОПРОТИВЛЕ́НИЕ, сопротивления, мн. нет, ср. (книжн.).
1. Действие по гл. сопротивляться. Оказывать сопротивление врагу. Сопротивление организма ядам. Сопротивление неприятеля.
2. Свойство, способность оказывать противодействие каким-нибудь воздействиям, изменениям. Сопротивление электрическое (степень электропроводимости тел). Сопротивление среды (свойство среды тормозить движение тал).
• По линии наименьшего сопротивления - см. линия. Сопротивление материалов - 1) свойство материалов противодействовать изменению их форм; 2) наука, изучающая явления деформации и исследующая общие методы расчета машин и сооружений.
СОПРОТИВЛЕ́НИЕ, -я, ср.
1. см. сопротивляться.
2. (С прописное). В странах Западной Европы в годы фашистской оккупации: народное движение против захватчиков. Участник Сопротивления. В годы Сопротивления.
СОПРОТИВЛЕ́НИЕ, -я, ср (С прописное).
Деятельность народов Западной Европы против захватчиков в годы фашистской оккупации; антифашистское народное движение.
Военные имеют более четырех миллионов людей, организованных в мощный кулак Сопротивления (Ю. Сем.).
СОПРОТИВЛЕ́НИЕ -я; ср.
1. к Сопротивля́ться. С. деспотической власти. Наши части встретили отчаянное с. противника. Сдаться без сопротивления. Быть готовым к сопротивлению. Призывать к сопротивлению. Оказать с. Преодолеть внутреннее с. (о внутренней борьбе с самим собой при совершении каких-л. действий, поступков).
2. Физ., техн. Свойство, способность (материалов, сооружений и т.п.), противостоять каким-л. воздействиям, изменениям. С. материалов (также: наука о прочности и видах деформации материалов и элементов машин и сооружений). Электрическое с. (способность проводника препятствовать движению электрического тока).
3. В странах Западной Европы в годы фашистской оккупации: народное движение против захватчиков. Участник Сопротивления. В годы Сопротивления.
◊ Пойти по линии (по пути) наименьшего сопротивле́ния. Выбрать самый лёгкий способ решения чего-л., уклониться от трудностей, неприятностей.
-я, ср.
1. Действие по глаг. сопротивляться (в 1 знач.).
Отец восстал против деспотической власти деда, а дед не мог примириться с дерзким сопротивлением отца. Гладков, Повесть о детстве.
|| воен.
Военные действия, связанные с противодействием воинских частей противнику.
Необходимо немедленно принять самые решительные меры к преодолению сопротивления противника. Степанов, Порт-Артур.
2. физ.
Свойство, способность тел оказывать противодействие каким-л. воздействиям, изменениям.
Электрическое сопротивление (способность противодействовать протеканию электрического тока).
◊
сопротивление материалов
физ., тех.
1) способности материалов противодействовать изменению их формы;
2) наука о прочности и видах деформации материалов и элементов конструкций машин и сооружений.
- пойти по линии наименьшего сопротивления
сопротивле́ние, -я (проти-водействие) и Сопротивле́ние, -я (антифашист-ское движение в годы Второй мировой войны; движе́ние Сопротивле́ния)
сопротивле́ние, сопротивле́ния, сопротивле́ний, сопротивле́нию, сопротивле́ниям, сопротивле́нием, сопротивле́ниями, сопротивле́нии, сопротивле́ниях
сущ., кол-во синонимов: 20
борьба (34)
возражение (15)
воспротивление (1)
гридлик (1)
импеданс (2)
облуктация (2)
обструкция (7)
оппозиция (8)
отпор (4)
протест (17)
противление (3)
противоборство (15)
противодействие (18)
реактанц (2)
супротивность (2)
упор (17)
1.
Syn: отпор, противодействие, противоборство, противление, борьба
Ant: подчинение
2.
Syn: прочность, резистанс
активное сопротивление
бешеное сопротивление
большое сопротивление
наибольшее сопротивление
неистовое сопротивление
неслыханное сопротивление
ожесточенное сопротивление
отчаянное сопротивление
серьезное сопротивление
сильное сопротивление
яростное сопротивление
▲ , реакция (на)
↑ негативный, внешнее воздействие
<-> поддаваться
сопротивление - негативная реакция на внешнее воздействие (отчаянное #).
сопротивляться - стремиться подавить внешнее действие;
оказывать противодействие, препятствие внешнему действию;
не поддаваться внешнему воздействию.
оказывать сопротивление.
↓ ПРОЧНОСТЬ, устойчивость, выносливость человека
▼ трение
(не) встретить сопротивления => действие, получатель
(не) встречать сопротивления => действие, получатель
встретить упорное сопротивление => действие, получатель
оказать сопротивление => действие
оказывать сопротивление => действие
прекратить сопротивление => действие, прерывание
преодолевать сопротивление => действие, прерывание
сломить сопротивление => действие, прерывание
- «Женщины с обтекаемыми формами оказываются наибольшее ...» (шутка).
- Активное неподчинение.
- Реакция пружины на сжатие.
- Что измеряется в омах?
- Противодействие цепи электрического тока движущимся электронам.
СОПРОТИВЛЯ́ТЬСЯ, -я́юсь, -я́ешься; несов., кому-чему. Противодействовать натиску, нападению, воздействию кого-чего-н. С. врагу. С. болезни.
Сопротивле́ние материа́лов - наука о прочности и деформируемости элементов сооружений и деталей машин. Основные объекты изучения - стержни и пластины, исследуемые теоретическими и экспериментальными методами. Главная задача сопротивления материалов - создание методов расчёта элементов (деталей) на прочность, жёсткость, устойчивость и колебания при действии статических и динамических нагрузок. Эти методы используются в инженерной практике для определения наибольших напряжений и перемещений в элементах и сравнения их с нормативными величинами, безопасными для эксплуатации сооружения (машины).
* * *
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ - СОПРОТИВЛЕ́НИЕ МАТЕРИА́ЛОВ, наука о прочности и деформируемости элементов сооружений и деталей машин. Основные объекты изучения - стержни и пластины, исследуемые теоретическими и экспериментальными методами. Главная задача сопротивления материалов - создание методов расчета элементов (деталей) на прочность, жесткость, устойчивость и колебания при действии статической и динамической нагрузок. Эти методы используются в инженерной практике для определения наибольших напряжений и перемещений в элементах и сравнения их с нормативными величинами, безопасными для эксплуатации сооружения (машины).
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ - наука о прочности и деформируемости элементов сооружений и деталей машин. Основные объекты изучения - стержни и пластины, исследуемые теоретическими и экспериментальными методами. Главная задача сопротивления материалов - создание методов расчета элементов (деталей) на прочность, жесткость, устойчивость и колебания при действии статической и динамической нагрузок. Эти методы используются в инженерной практике для определения наибольших напряжений и перемещений в элементах и сравнения их с нормативными величинами, безопасными для эксплуатации сооружения (машины).
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ - раздел механики твердого тела, изучающий напряжения и деформации, которые обусловлены силами, действующими на твердые тела - элементы конструкции. Эту дисциплину можно характеризовать и как науку о методах расчета элементов конструкции на прочность, жесткость и устойчивость. Напряжение, создаваемое в твердом теле внешними нагрузками, есть мера (с размерностью силы на единицу площади) интенсивности внутренних сил, действующих со стороны одной, мысленно отсекаемой, части тела на другую, оставшуюся (метод сечений). Внешние нагрузки вызывают деформацию тела, т.е. изменение его размеров и формы. В сопротивлении материалов исследуются соотношения между нагрузками, напряжениями и деформациями, причем исследования ведутся, с одной стороны, путем математического вывода формул, связывающих нагрузки с вызываемыми ими напряжениями и деформациями, а с другой - путем экспериментального определения характеристик материалов, применяемых в строениях и машинах.
См. также
МЕТАЛЛОВ МЕХАНИЧЕСКИЕ СВОЙСТВА;
По найденным формулам с учетом результатов испытания материалов рассчитываются размеры элементов строений и машин, обеспечивающие сопротивление заданным нагрузкам. Сопротивление материалов не относится к точным наукам, так как многие его формулы выводятся на основе предположений о поведении материалов, которые не всегда точно выполняются. Тем не менее, пользуясь ими, грамотный инженер может создавать надежные и экономичные конструкции. С сопротивлением материалов тесно связана математическая теория упругости, в которой тоже рассматриваются напряжения и деформации. Она позволяет решать те задачи, которые с трудом поддаются решению обычными методами сопротивления материалов. Однако между сопротивлением материалов и теорией упругости нет четкой границы. Хотя почти все задачи о распределении напряжений решены методами математического анализа, при сложных условиях эти решения требуют трудоемких выкладок. И тогда на помощь приходят экспериментальные методы анализа напряжений.
НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ
Виды напряжений. Самое важное понятие в сопротивлении материалов - это понятие напряжения как силы, действующей на малую площадку и отнесенной к площади этой площадки. Напряжения бывают трех видов: растяжения, сжатия и сдвига. Если на металлическом стержне подвешен груз, как показано на рис. 1,а, то такой стержень называется растянутым или работающим на растяжение. Напряжение S, создаваемое силой P в растянутом стержне с площадью поперечного сечения, равной A, дается выражением S = P/A. Если вес груза равен 50 000 Н, то растягивающая сила тоже равна 50 000 Н. Далее, если ширина стержня равна 0,05 м, а толщина - 0,02 м, так что площадь поперечного сечения составляет 0,001 м2, то растягивающее напряжение равно 50 000/0,001 = 50 000 000 Н/м2 = 50 МПа. Растянутый стержень длиннее, чем до приложения растягивающих сил.
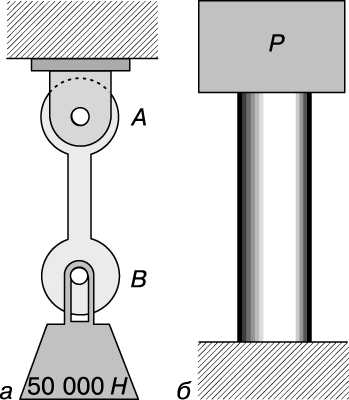
Рис. 1. РАСТЯНУТЫЙ (а) И СЖАТЫЙ (б) СТЕРЖНИ
Рассмотрим короткий цилиндр (рис. 1,б), на верхний торец которого положен груз. При этом во всех поперечных сечениях цилиндра действуют напряжения сжатия. Если напряжение равномерно распределено по всему сечению, то справедлива формула S = P/A. Сжатый цилиндр короче, чем в отсутствие деформаций. Напряжение сдвига возникает, например, в болте (рис. 2,а), на котором верхним концом держится растянутый стержень AB с грузом 50 000 Н (рис. 1,а). Болт удерживает стержень, действуя с силой 50 000 Н, направленной вверх, на ту часть стержня, которая расположена непосредственно над отверстием в стержне, а стержень в свою очередь давит на среднюю часть болта с силой 50 000 Н. Силы, действующие на болт, приложены так, как показано на рис. 2,б. Если бы болт был сделан из материала с низким пределом прочности на сдвиг, например из свинца, то он был бы срезан по двум вертикальным плоскостям (рис. 2,в). Если же болт стальной и достаточно большого диаметра, то он не срежется, но в двух его вертикальных поперечных сечениях будут существовать напряжения сдвига. Если напряжения сдвига равномерно распределены, то они даются формулой S = P/A. Полная сила сдвига, действующая в каждом из поперечных сечений, равна 25 000 Н, и если диаметр болта равен 0,02 м (площадь поперечного сечения равна приблизительно 0,0003 м2), то напряжение сдвига Ss будет составлять 25 000 Н/0,0003 м2, т.е. немногим более 80 МПа.
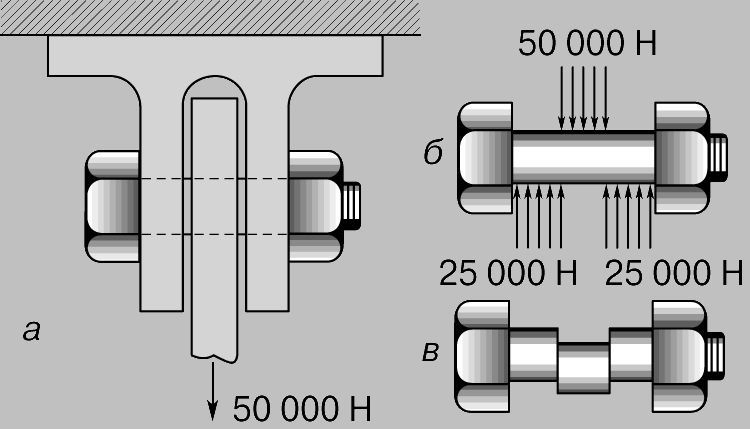
Рис. 2. НАПРЯЖЕНИЯ СДВИГА В БОЛТЕ
Напряжения растяжения и сжатия направлены по нормали (т.е. вдоль перпендикуляра) к площадке, в которой они действуют, а напряжение сдвига - параллельно площадке. Поэтому напряжения растяжения и сжатия называются нормальными, а напряжения сдвига - касательными.
Деформация. Деформацией называется изменение размера тела под действием приложенных к нему нагрузок. Деформация, отнесенная к полному размеру, называется относительной. Если изменение каждого малого элемента длины тела одинаково, то относительная деформация называется равномерной. Относительную деформацию часто обозначают символом d, а полную - символом D. Если относительная деформация постоянна по всей длине L, то d = D/L. Например, если длина стального стержня до приложения растягивающей нагрузки равна 2,00 м, а после нагружения - 2,0015 м, то полная деформация D равна 0,0015 м, а относительная - d = 0,0015/2,00 = 0,00075 (м/м). Почти для всех материалов, применяемых в строениях и машинах, относительная деформация пропорциональна напряжению, пока оно не превысит т.н. предела пропорциональности. Это очень важное соотношение называется законом Гука. Оно было экспериментально установлено и сформулировано в 1678 английским изобретателем и часовых дел мастером Р.Гуком. Данное соотношение между напряжением и деформацией для любого материала выражается формулой S = Ed, где E - постоянный множитель, характеризующий материал. Этот множитель называют модулем Юнга по имени Т.Юнга, который ввел его в 1802, или же модулем упругости. Из обычных конструкционных материалов наибольший модуль упругости у стали; он равен примерно 200 000 МПа. В стальном стержне относительная деформация, равная 0,00075, из приводившегося ранее примера вызывается напряжением S = Ed = 200 000ґ0,00075 = 150 МПа, что меньше предела пропорциональности конструкционной стали. Если бы стержень был из алюминия с модулем упругости около 70 000 МПа, то, чтобы вызвать ту же самую деформацию 0,00075, достаточно было бы напряжения немногим более 50 МПа. Из сказанного ясно, что упругие деформации в строениях и машинах очень малы. Даже при сравнительно большом напряжении 150 МПа из приведенного выше примера относительная деформация стального стержня не превышает одной тысячной. Столь большая жесткость стали - ее ценное качество. Чтобы наглядно представить деформацию сдвига, рассмотрим, например, прямоугольную призму ABCD (рис. 3). Ее нижний конец жестко заделан в твердое основание. Если на верхнюю часть призмы действует горизонтальная внешняя сила F, она вызывает деформацию сдвига, показанную штриховыми линиями. Смещение D есть полная деформация на длине (высоте) L. Относительная деформация сдвига d равна D/L. Для деформации сдвига тоже выполняется закон Гука при условии, что напряжение не превышает предела пропорциональности для сдвига. Следовательно, Ss = Esd, где Es - модуль сдвига. Для любого материала величина Es меньше E. Для стали она составляет около 2/5 E, т.е. приблизительно 80 000 МПа. Важный случай деформации сдвига - деформация в валах, на которые действуют внешние скручивающие моменты.
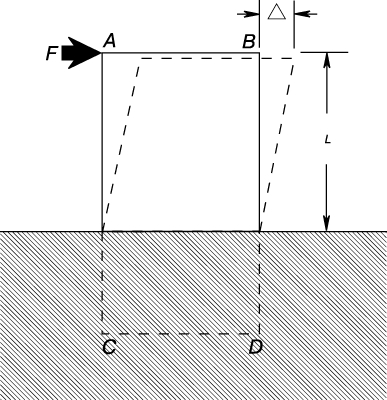
Рис. 3. ДЕФОРМАЦИЯ СДВИГА определяется как смещение D, отнесенное к исходной высоте L.
Выше речь шла об упругих деформациях, которые вызываются напряжениями, не превышающими предела пропорциональности. Если же напряжение выходит за предел пропорциональности, то деформация начинает расти быстрее, чем напряжение. Закон Гука перестает быть справедливым. В случае конструкционной стали в области, лежащей чуть выше предела пропорциональности, небольшое увеличение напряжения приводит к увеличению деформации во много раз по сравнению с деформацией, соответствующей пределу пропорциональности. Напряжение, при котором начинается столь быстрый рост деформации, называется пределом текучести. Материал, в котором разрушению предшествует большая неупругая деформация, называется пластичным.
ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ
Допускаемое (допустимое) напряжение - это значение напряжения, которое считается предельно приемлемым при вычислении размеров поперечного сечения элемента, рассчитываемого на заданную нагрузку. Можно говорить о допускаемых напряжениях растяжения, сжатия и сдвига. Допускаемые напряжения либо предписываются компетентной инстанцией (скажем, отделом мостов управления железной дороги), либо выбираются конструктором, хорошо знающим свойства материала и условия его применения. Допускаемым напряжением ограничивается максимальное рабочее напряжение конструкции. При проектировании конструкций ставится цель создать конструкцию, которая, будучи надежной, в то же время была бы предельно легкой и экономной. Надежность обеспечивается тем, что каждому элементу придают такие размеры, при которых максимальное рабочее напряжение в нем будет в определенной степени меньше напряжения, вызывающего потерю прочности этим элементом. Потеря прочности не обязательно означает разрушение. Машина или строительная конструкция считается отказавшей, когда она не может удовлетворительно выполнять свою функцию. Деталь из пластичного материала, как правило, теряет прочность, когда напряжение в ней достигает предела текучести, так как при этом из-за слишком большой деформации детали машина или конструкция перестает соответствовать своему назначению. Если же деталь выполнена из хрупкого материала, то она почти не деформируется, и потеря ею прочности совпадает с ее разрушением.
Запас прочности. Разность напряжения, при котором материал теряет прочность, и допускаемого напряжения есть тот "запас прочности", который необходимо предусматривать, учитывая возможность случайной перегрузки, неточностей расчета, связанных с упрощающими предположениями и неопределенными условиями, наличия не обнаруженных (или не обнаружимых) дефектов материала и последующего снижения прочности из-за коррозии металла, гниения дерева и пр.
Коэффициент запаса. Коэффициент запаса прочности какого-либо элемента конструкции равен отношению предельной нагрузки, вызывающей потерю прочности элемента, к нагрузке, создающей допускаемое напряжение. При этом под потерей прочности понимается не только разрушение элемента, но и появление в нем остаточных деформаций. Поэтому для элемента конструкции, выполненного из пластичного материала, предельным напряжением является предел текучести. В большинстве случаев рабочие напряжения в элементах конструкции пропорциональны нагрузкам, а поэтому коэффициент запаса определяется как отношение предела прочности к допускаемому напряжению (коэффициент запаса по пределу прочности). Так, если предел прочности конструкционной стали равен 540 МПа, а допускаемое напряжение - 180 МПа, то коэффициент запаса равен 3.
РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ
В сопротивлении материалов большое внимание уделяется выводу соотношений между заданными нагрузками, размерами и формой элемента конструкции, несущего эти нагрузки или сопротивляющегося им, и напряжениями, возникающими в определенных сечениях элемента конструкции. Как правило, цель расчетов состоит в том, чтобы найти необходимые размеры элемента, при которых максимальное рабочее напряжение в нем не будет превышать допускаемого. В элементарном курсе сопротивления материалов рассматривается ряд типичных случаев равномерного распределения напряжений: растянутые стержни, короткие сжатые стержни, тонкостенные цилиндры, работающие под давлением внутренней среды (котлы и резервуары), заклепочные и сварные соединения, температурные напряжения и такие статически неопределимые системы, как растянутые стержни из нескольких разных материалов. Если напряжение одинаково во всех точках поперечного сечения, то S = P/A. Конструктор находит необходимую площадь поперечного сечения, поделив заданную нагрузку на допускаемое напряжение. Но нужно уметь отличать случаи, в которых напряжение действительно распределено равномерно, от других, сходных случаев, в которых этого нет. Необходимо также (как в задаче о заклепочных соединениях, в которых существуют напряжения и растяжения, и сжатия, и сдвига) находить плоскости, в которых действуют напряжения разного вида, и определять максимальные местные напряжения.
Тонкостенный цилиндр. Такой резервуар выходит из строя (разрывается), когда напряжение растяжения в его оболочке становится равным пределу прочности материала. Формулу, связывающую толщину стенки t, внутренний диаметр резервуара D, напряжение S и внутреннее давление R, можно вывести, рассмотрев условия равновесия кольца, вырезанного из его оболочки двумя поперечными плоскостями, разделенными расстоянием L (рис. 4,а). Внутреннее давление действует на внутреннюю поверхность полукольца с направленной вверх силой, равной произведению RDL, а напряжения в двух горизонтальных концевых сечениях полукольца создают две направленные вниз силы, каждая из которых равна tLS. Приравнивая, получаем RDL = 2tLS, откуда S = RD/2t.
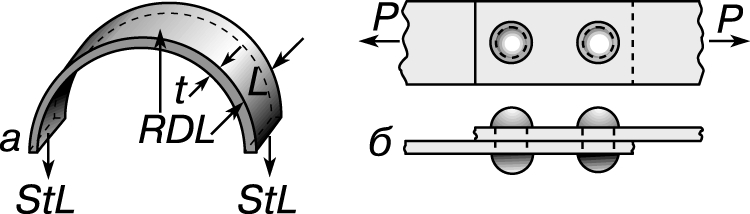
Рис. 4. ЭЛЕМЕНТ ТОНКОСТЕННОГО ЦИЛИНДРА (а) и двухзаклепочное соединение внахлестку (б).
Заклепочное соединение. На рис. 4,б представлено двухзаклепочное соединение двух полос внахлестку. Такое соединение может выйти из строя из-за перерезывания обеих заклепок, разрыва одной из полос в том месте, где она ослаблена отверстием под заклепку, или из-за слишком больших напряжений смятия по площади соприкосновения заклепки с полосой. Напряжение смятия в заклепочном соединении вычисляется как нагрузка на одну заклепку, деленная на диаметр заклепки и на толщину полосы. Допускаемой для такого соединения принимается наименьшая из нагрузок, соответствующих допускаемым напряжениям трех указанных видов. Вообще говоря, напряжение, действующее в поперечном сечении растянутого или короткого сжатого стержня, можно с полным основанием считать равномерно распределенным, если равные и противоположно направленные нагрузки приложены так, что равнодействующая каждой из них проходит через центр тяжести рассматриваемого поперечного сечения. Но нужно иметь в виду, что ряд задач (и к ним относится задача о напряжениях смятия в заклепочном соединении) решается в предположении о равномерном распределении напряжения, хотя это заведомо не соответствует действительности. Допустимость такого подхода проверяется опытным путем.
НЕРАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ
Многие элементы строений и детали машин нагружаются так, что напряжения во всех их поперечных сечениях распределены неравномерно. Чтобы вывести формулы для расчета напряжений в таких условиях, мысленно разрезают элемент плоскостью, которая дает нужное поперечное сечение, на две части и рассматривают условия равновесия одной из них. На эту часть действуют одна или несколько заданных внешних сил, а также силы, эквивалентные напряжениям в данном поперечном сечении. Действующие напряжения должны удовлетворять условиям равновесия и соответствовать деформациям. Эти два требования составляют основу для решения задачи. Второе из них подразумевает справедливость закона Гука. Типичными элементами с неравномерным распределением напряжений являются нагруженные балки, валы под действием скручивающих сил, растянутые или сжатые стержни с дополнительным изгибом и колонны.
БАЛКИ
Балка - это длинный стержень с опорами и нагрузками, работающий в основном на изгиб. Поперечное сечение балки обычно одинаково по всей ее длине. Силы, с которыми опоры действуют на балку, называются реакциями опор. Наиболее распространены два вида балок: консольная (рис. 5,а) и балка с двумя опорами, называемая простой (рис. 5,б). Под действием нагрузок балка прогибается. При этом "волокна" на ее верхней стороне сокращаются, а на нижней - удлиняются. Очевидно, что где-то между верхней и нижней сторонами балки имеется тонкий слой, длина которого не изменяется. Он называется нейтральным слоем. Изменение длины волокна, расположенного между верхней (или нижней) стороной балки и ее нейтральным слоем, пропорционально расстоянию до нейтрального слоя. Если справедлив закон Гука, то напряжения тоже пропорциональны этому расстоянию.
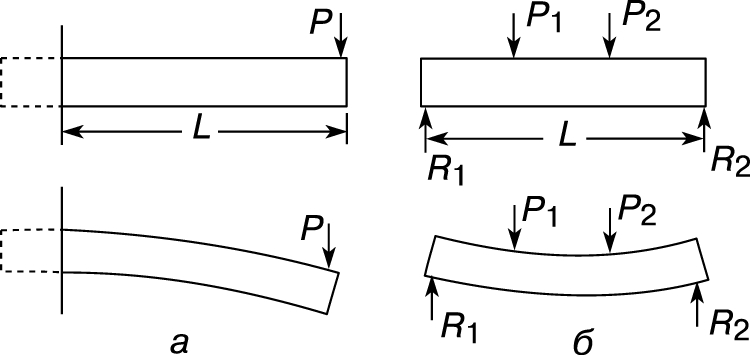
Рис. 5. ДВА ТИПА БАЛОК: а - консольная, б - простая. P, P1 и P2 - сосредоточенные нагрузки; R1 и R2 - реакции опор; L - длина.
Формула изгиба. На основе указанного распределения напряжений, дополненного условиями статики, выведена т.н. формула изгиба, в которой напряжение выражается через нагрузки и размеры балки. Она обычно представляется в виде S = Mc/I, где S - максимальное напряжение в рассматриваемом поперечном сечении, c - расстояние от нейтрального слоя до наиболее напряженного волокна, M - изгибающий момент, равный сумме моментов всех сил, действующих по одну сторону от этого сечения, а I - момент инерции поперечного сечения (определенная функция формы и размеров последнего). Характер изменения нормальных напряжений в поперечном сечении балки показан на рис. 6.
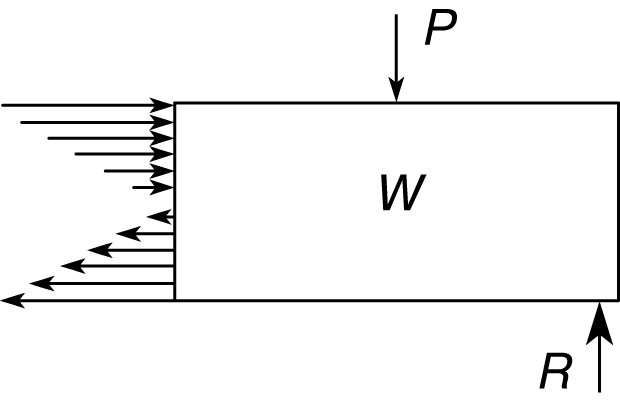
Рис. 6. РАСПРЕДЕЛЕНИЕ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ в поперечном сечении балки. P - нагрузка, R - реакция, W - вес (распределенная нагрузка).
В поперечных сечениях балок действуют также касательные напряжения. Их вызывает равнодействующая всех вертикальных сил, приложенных по одну сторону поперечного сечения горизонтальной балки. Сумма всех внешних сил и реакций, действующих на одну из двух частей балки, называется сдвигом в сечении балки и обычно обозначается через V. Касательные напряжения неравномерно распределены по сечению: они равны нулю на верхнем и нижнем краях сечения и почти всегда максимальны в нейтральном слое.
Прогиб балки. Часто требуется рассчитать прогиб балки, вызванный действием нагрузки, т.е. вертикальное смещение точки, лежащей в нейтральном слое. Это очень важная задача, поскольку прогиб и кривизну балки нужно знать при решении задач, относящихся к широкому кругу т.н. статически неопределимых систем. Еще в 1757 Л. Эйлер вывел формулу для кривизны изогнутой балки. В этой формуле кривизна балки выражается через переменный изгибающий момент. Чтобы найти ординату упругой кривой (прогиб), необходимо брать двойной интеграл. В 1868 О.Мор (Германия) предложил метод, основанный на эпюрах изгибающих моментов. Этот графоаналитический метод имеет огромное преимущество перед прежними методами, так как позволяет свести все математические вычисления к сравнительно простым арифметическим выкладкам. Он дает возможность вычислять прогиб и наклон в любой точке балки при любой нагрузке.
Статически неопределимые балки. Многие балки, используемые в строениях и машинах, имеют более двух опор или только две опоры, но с заделкой одного из концов, исключающей возможность поворота. Такие балки называются статически неопределимыми, поскольку уравнений статики недостаточно для определения реакций в опорах и моментов в заделке. Чаще всего рассматриваются подобные балки трех типов: с одним заделанным (защемленным) концом и одной опорой, с заделанными обоими концами и неразрезные балки, имеющие более двух опор (рис. 7).
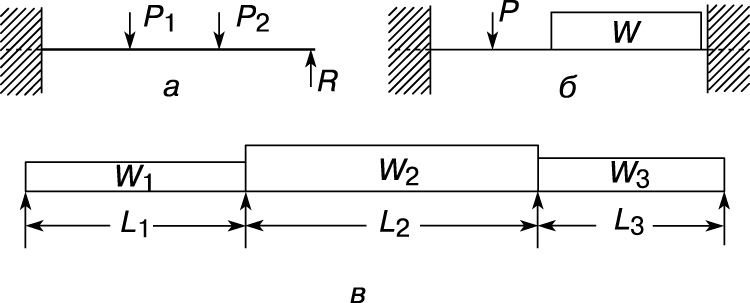
Рис. 7. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ БАЛКИ: а - с одним заделанным концом; б - с двумя заделанными концами; в - неразрезная трехпролетная. P, P1, P2 - сосредоточенные нагрузки; R - реакция; L1, L2, L3 - длины; W, W1, W2, W3 - веса (распределенные нагрузки).
Первое решение задачи о неразрезных балках было опубликовано французским инженером Б. Клапейроном в 1857. Он доказал т. н. теорему о трех моментах. Уравнение трех моментов представляет собой соотношение между изгибающими моментами в трех последовательных опорах одной неразрезной балки. Например, в случае неразрезной балки с равномерной нагрузкой на каждом пролете это уравнение имеет вид MAL1 + 2MB (L1 + L2) + MCL2 = - (W1L13)/4 - (W2L23)/4. Здесь MA, MB и MC - изгибающие моменты в трех опорах, L1 и L2 - длины левого и правого пролетов, W1 - нагрузка на левый пролет, а W2 - нагрузка на правый пролет. Нужно написать такое уравнение для каждой пары смежных пролетов, а затем решить полученную систему уравнений. Если число пролетов равно n, то число уравнений будет равно n - 1. В 1930 Х. Кросс опубликовал свой метод расчета широкого круга статически неопределимых рам и неразрезных балок. Его "метод распределения моментов" позволяет обходиться без решения систем уравнений, сводя все вычисления к сложению и вычитанию чисел.
НАПРЯЖЕНИЕ ПРИ КРУЧЕНИИ
Если к концам вала приложены равные, но противоположно направленные внешние скручивающие моменты, то во всех его поперечных сечениях существуют только касательные напряжения, т.е. напряженное состояние в точках скручиваемого стержня представляет собой чистый сдвиг. В круговом поперечном сечении вала деформации сдвига и касательные напряжения равны нулю в центре и максимальны на краю; в промежуточных точках они пропорциональны расстоянию от центра тяжести сечения. Обычная формула для максимального касательного напряжения при кручении такова: S = Tc/J, где T - скручивающий момент на одном конце, c - радиус вала и J - полярный момент сечения. Для круга J = pr4/2. Эта формула применима только в случае кругового поперечного сечения. Формулы для валов с поперечным сечением другой формы выводятся путем решения соответствующих задач методами математической теории упругости с привлечением в некоторых случаях методов экспериментального анализа.
СЛОЖНОЕ СОПРОТИВЛЕНИЕ
Нередко приходится рассчитывать балки, на которые в дополнение к поперечным нагрузкам действуют продольные силы растяжения или сжатия, приложенные к концам. В таких случаях напряжение в любой точке поперечного сечения равно алгебраической сумме нормального напряжения, создаваемого продольной нагрузкой, и изгибного напряжения, создаваемого поперечными нагрузками. Общая формула для напряжения в случае совместного действия изгиба и растяжения-сжатия такова: S = ± (P/A) ± (Mc/I), где знак "плюс" относится к растягивающему напряжению.
КОЛОННЫ
Каркасы зданий и фермы мостов состоят в основном из растянутых стержней, балок и колонн. Колонны - это длинные сжатые стержни, примером которых в каркасах зданий могут служить вертикальные стержни, несущие межэтажные перекрытия. Если длина сжатого стержня более чем в 10-15 раз превышает его толщину, то под действием критических нагрузок, приложенных к его концам, он, потеряв устойчивость, изогнется, даже если нагрузки номинально приложены по его оси (продольный изгиб). Вследствие такого изгиба нагрузка оказывается внецентренной. Если эксцентриситет в среднем поперечном сечении колонны равен D, то максимальное сжимающее напряжение в колонне будет равно (P/A) + (PDc/I). Отсюда видно, что допускаемая нагрузка для колонны должна быть меньше, чем для короткого сжатого стержня. Формулу для устойчивости гибких колонн вывел в 1757 Л. Эйлер. Максимальная нагрузка P, которую может нести гибкая колонна высотой L, равна mEA /(L/r)2, где m - постоянный множитель, зависящий от конструкции основания, A - площадь поперечного сечения колонны, а r - наименьший радиус инерции поперечного сечения. Отношение L/r называется гибкостью (при продольном изгибе). Как нетрудно видеть, допускаемая нагрузка быстро убывает с увеличением гибкости колонны. В случае колонн с малой гибкостью формула Эйлера непригодна, и конструкторы вынуждены пользоваться эмпирическими формулами. В строениях часто встречаются внецентренно нагруженные колонны. В результате точного теоретического анализа таких колонн были получены "формулы секанса". Но расчеты по этим формулам весьма трудоемки, а потому часто приходится прибегать к эмпирическим методам, дающим хорошие результаты.
СЛОЖНЫЕ НАПРЯЖЕННЫЕ СОСТОЯНИЯ
Напряжение в какой-либо точке той или иной плоскости нагруженного тела, вычисленное по обычным формулам, не обязательно будет наибольшим в этой точке. Поэтому важное значение имеет вопрос о соотношениях между напряжениями в разных плоскостях, проходящих через одну точку. Такие соотношения являются предметом раздела механики, посвященного сложным напряженным состояниям.
Соотношения между напряжениями. Напряженное состояние в некоторой точке любого нагруженного тела можно полностью охарактеризовать, представив напряжения, действующие на грани элементарного куба в этой точке. Часто встречаются случаи, к которым относятся и рассмотренные выше, двухосного (плоского) напряженного состояния с напряжениями, равными нулю, на двух противоположных гранях куба. Напряжения, существующие в точке тела, неодинаковы в плоскостях с разным наклоном. Исходя из основных положений статики, можно сделать ряд важных выводов о соотношении между напряжениями в разных плоскостях. Приведем три из них: 1. Если в некоторой точке заданной плоскости имеется касательное напряжение, то точно такое же напряжение имеется в проходящей через эту точку плоскости, перпендикулярной заданной. 2. Существует плоскость, в которой нормальное напряжение больше, чем в любой другой. 3. В плоскости, перпендикулярной этой плоскости, нормальное напряжение меньше, чем в какой-либо другой. Максимальное и минимальное нормальные напряжения, о которых говорится в п. 2 и 3, называются главными напряжениями, а соответствующие плоскости - главными плоскостями. Необходимость в анализе главных напряжений на основе указанных соотношений не всегда возникает, так как простые формулы, которыми обычно пользуются инженеры, в большинстве случаев дают именно максимальные напряжения. Но в некоторых случаях, например при расчете вала, сопротивляющегося одновременно скручивающему и изгибающему моментам, нельзя обойтись без соотношений для сложного напряженного состояния.
БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ
В задачах, о которых говорилось выше, рассматривались напряжения либо равномерно распределенные, либо линейно меняющиеся с удалением от нейтральной оси, где напряжение равно нулю. Однако во многих случаях закон изменения напряжения более сложен. В качестве примера задач с нелинейным распределением напряжений можно привести искривленные балки, толстостенные сосуды, работающие под высоким внутренним или наружным давлением, валы некругового поперечного сечения и нагруженные тела с резкими изменениями поперечного сечения (канавками, буртиками и т.д.). Для таких задач рассчитываются коэффициенты концентрации напряжений. Кроме того, выше речь шла только о статических нагрузках, постепенно прилагаемых и снимаемых. Переменные же и периодически меняющиеся нагрузки, многократно повторенные, могут приводить к потере прочности, даже если они не превышают статического предела прочности рассматриваемого материала. Такие отказы называются усталостными, а проблема их предотвращения приобрела важное значение в наш век машин и механизмов, работающих на необычайно высоких скоростях.
См. также
ПРОЧНОСТНОЙ РАСЧЕТ КОНСТРУКЦИИ;
КОНСТРУКЦИОННЫЕ И СТРОИТЕЛЬНЫЕ МАТЕРИАЛЫ.
ЛИТЕРАТУРА
Беляев Н.М. Сопротивление материалов. М., 1978 Павлов П.А. Механические состояния и прочность материалов. Л., 1980 Биргер И.А., Мавлютов Р.Р. Сопротивление материалов. М., 1986 Писаренко Г.С. и др. Сопротивление материалов. Киев, 1986 Степин П.А. Сопротивление материалов. М., 1988 Бородин Н.А. Сопротивление материалов. М., 1992
▲ наука, ↑ определение (неявного), прочность
расчетная схема.
расчет сооружений.
строительная механика.
Сопротивле́ние электри́ческое - величина, характеризующая противодействие электрической цепи (или её участка) электрическому току. Электрическое сопротивление обусловлено преобразованием электрической энергии в другие виды энергии; при необратимом преобразовании (преимущественно в теплоту). Электрическое сопротивление называют активным сопротивлением; электрическое сопротивление, обусловленное передачей энергии электрическому или магнитному полю (и обратно), называют реактивным сопротивлением.
* * *
СОПРОТИВЛЕНИЕ ЭЛЕКТРИЧЕСКОЕ - СОПРОТИВЛЕ́НИЕ ЭЛЕКТРИ́ЧЕСКОЕ,
1) Величина, характеризующая противодействие электрической цепи (или ее участка) электрическому току.
При постоянном токе (см. ПОСТОЯННЫЙ ТОК) электрическое сопротивление цепи R можно определить в соответствии с законом Ома (см. ОМА ЗАКОН). Электрическое сопротивление цепи равно отношению приложенного к ней напряжения (см. НАПРЯЖЕНИЕ (электрическое)) U к силе тока (см. СИЛА ТОКА) I, протекающего в ней (при отсутствии в цепи других источников тока или электродвижущей силы (см. ЭЛЕКТРОДВИЖУЩАЯ СИЛА)).
R = U/I.
Такое сопротивление называют омическим или активным сопротивлением (см. АКТИВНОЕ СОПРОТИВЛЕНИЕ). Активное сопротивление элемента электрической цепи зависит как от формы элемента и его размеров, так и от материала, из которого он изготовлен. Для однородного по составу элемента с удельным сопротивлением (см. УДЕЛЬНОЕ СОПРОТИВЛЕНИЕ) , изготовленным в виде бруска, пластины, трубки или проволоки при постоянном его сечении S и длине l, электрическое сопротивление
R = l/S
При очень низких температурах электрическое сопротивление некоторых веществ падает до нуля (см. Сверхпроводники (см. СВЕРХПРОВОДНИКИ)).
Электрическое активное сопротивление обусловлено преобразованием электрической энергии в другие виды энергии (преимущественно в теплоту). Такое преобразование в активных сопротивлениях носит необратимый характер.
Величина электрического сопротивления зависит от температуры. Характер температурной зависимости определяется природой вещества, т. е. механизмом проводимости. Сопротивление металлов при повышении температуры возрастает, а полупроводников и электролитов - падает.
В СИ единицей электрического сопротивления проводников является ом (см. ОМ (единица измерения)) (Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.
Электрическое сопротивление, обусловленное передачей энергии электрическому или магнитному полю (и обратно), называется реактивным сопротивлением (см. РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ). В цепи переменного тока (см. ПЕРЕМЕННЫЙ ТОК) проводник помимо активного сопротивления обладает еще и емкостным сопротивлением (см. ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ) и индуктивным сопротивлением (см. ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ).
Электрическое сопротивление измеряют омметрами или измерительными мостами.
2) Структурный элемент электрической цепи, включаемый в цепь для ограничения или регулирования силы тока.
СОПРОТИВЛЕНИЕ ЭЛЕКТРИЧЕСКОЕ - величина, характеризующая противодействие электрической цепи (или ее участка) электрическому току. Электрическое сопротивление обусловленно преобразованием электрической энергии в др. виды энергии: при необратимом преобразовании (преимущественно в теплоту). Электрическое сопротивление называется активным сопротивлением; электрическое сопротивление, обусловленное передачей энергии электрическому или магнитному полю (и обратно), называется реактивным сопротивлением.