Устар. То же, что Божия (божья) благодать (во 2-м знач.).

[Pater:] Вспомоществуй тебе святый Игнатий, Когда придут иные времена. А между тем небесной благодати Таи в душе, царевич, семена (Пушкин. Борис Годунов).

Составить слова из слова небесная благодать

сущ., кол-во синонимов: 9

высота, поднебесье, высь, эфир, небо, воздушное пространство, вышина, небесная лазурь, высота поднебесная

Составить слова из слова небесная высь

сущ., кол-во синонимов: 1

Составить слова из слова небесная гостья

Небе́сная импе́рия (об императорском Китае)

сущ., кол-во синонимов: 1

Составить слова из слова небесная империя

Нов. Ирон. О сверхъестественных силах, явлениях природы.

- А, всё у вас не как у людей! Даже обнять не дадут вовремя… Но всё равно молодцы! Всем чертям назло, всей небесной канцелярии! (А. Пряшников. Нестандартный Силантьев).

Архангелы или ещё кто там распоряжается в небесной канцелярии, ни одного облачка не запланировали с утра над землями Воронежа, однако люди распорядились по-своему - целый день гудом гудели громы, бушевали в полях огненные смерчи и гасло солнце в чёрном смраде дымовой облачности (В. Тишков. Последний редут).

Составить слова из слова небесная канцелярия

сущ., кол-во синонимов: 7

Составить слова из слова небесная лазурь

Небе́сная меха́ника - раздел астрономии, изучающий движения тел Солнечной системы в их общем гравитационном поле. В ряде случаев (в теории движения комет, ИСЗ и др.) кроме гравитационных сил учитываются реактивные силы, давление излучения, сопротивление среды, изменение массы и другие факторы. К проблемам небесной механики относится рассмотрение общих вопросов движения небесных тел в гравитационном поле (так называемая задача n тел, в частности трёх тел задача и двух тел задача) и движения конкретных объектов (планет, ИСЗ и т. д.); определение значений астрономических постоянных; составление эфемерид. Новый раздел небесной механики - релятивистская небесная механика, учитывающая в движении тел Солнечной системы эффекты общей теории относительности.

* * *

НЕБЕСНАЯ МЕХАНИКА - НЕБЕ́СНАЯ МЕХА́НИКА, раздел астрономии, изучающий движения тел Солнечной системы в их общем гравитационном поле. В ряде случаев (в теории движения комет, искусственный спутник Земли и др.), кроме гравитационных сил, учитываются реактивные силы, давление излучения, сопротивление среды, изменение массы и другие факторы. К проблемам Небесной механики относится рассмотрение общих вопросов движения небесных тел в гравитационном поле (т. н. задача n тел, в частности трех тел задача (см. ТРЕХ ТЕЛ ЗАДАЧА) и двух тел задача (см. ДВУХ ТЕЛ ЗАДАЧА)) и движения конкретных объектов (планет, искусственных спутников Земли и т. д.); определение значений астрономических постоянных; составление эфемерид. Новый раздел небесной механики - релятивистская небесная механика, учитывающая в движении тел Солнечной системы эффекты общей теории относительности.

НЕБЕСНАЯ механика - раздел астрономии, изучающий движения тел Солнечной системы в их общем гравитационном поле. В ряде случаев (в теории движения комет, искусственный спутник Земли и др.), кроме гравитационных сил, учитываются реактивные силы, давление излучения, сопротивление среды, изменение массы и другие факторы. К проблемам Небесной механики относится рассмотрение общих вопросов движения небесных тел в гравитационном поле (т. н. задача n тел, в частности трех тел задача и двух тел задача) и движения конкретных объектов (планет, искусственных спутников Земли и т. д.); определение значений астрономических постоянных; составление эфемерид. Новый раздел небесной механики - релятивистская небесная механика, учитывающая в движении тел Солнечной системы эффекты общей теории относительности.

НЕБЕСНАЯ МЕХАНИКА - раздел астрономии, применяющий законы механики для изучения движения небесных тел. Небесная механика занимается предвычислением положения Луны и планет, предсказанием места и времени затмений, в общем, определением реального движения космических тел. Естественно, что небесная механика в первую очередь изучает поведение тел Солнечной системы - обращение планет вокруг Солнца, спутников вокруг планет, движение комет и других малых набесных тел. Тогда как перемещение далеких звезд удается заметить, в лучшем случае, за десятилетия и века, движение членов Солнечной системы происходит буквально на глазах - за дни, часы и даже минуты. Поэтому его изучение стало началом современной небесной механики, рожденной трудами И.Кеплера (1571-1630) и И.Ньютона (1643-1727). Кеплер впервые установил законы планетного движения, а Ньютон вывел из законов Кеплера закон всемирного тяготения и использовал законы движения и тяготения для решения небесно-механических проблем, не охваченных законами Кеплера. После Ньютона прогресс в небесной механике в основном заключался в развитии математической техники для решения уравнений, выражающих законы Ньютона. Таким образом, принципы небесной механики - это "классика" в том смысле, что и сегодня они такие же, как во времена Ньютона.

Законы движения Ньютона. Чтобы лучше понять методы и результаты небесной механики, познакомимся с законами Ньютона и проиллюстрируем их простыми примерами.

Закон инерции. Согласно этому закону, в системе отсчета, движущейся без ускорения, каждое тело сохраняет состояние покоя или прямолинейного и равномерного движения, если на него не действует внешняя сила. Это противоречит положению аристотелевой физики, утверждающему, что для поддержания движения тела требуется сила. Закон Ньютона говорит, что внешняя сила необходима только для приведения тела в движение, для его остановки или для изменения направления и величины его скорости. Темп изменения скорости тела по величине или направлению называется "ускорением" и свидетельствует о том, что на тело действует сила.

Для небесных тел обнаруженное из наблюдений ускорение служит единственным указателем действующей на них внешней силы. Понятие о силе и ускорении позволяет с единой позиции объяснить движение всех тел в природе: от теннисного мяча до планет и галактик. Поскольку объект, движущийся по искривленной траектории, испытывает ускорение, было заключено, что Земля на ее орбите вокруг Солнца постоянно подвергается влиянию силы, которую назвали "гравитацией". Задача небесной механики состоит в том, чтобы определить действующую на небесное тело силу гравитации и выяснить, как она влияет на его движение.

Закон силы. Если к телу приложена сила, то оно движется ускоренно, причем чем больше сила, тем больше ускорение. Однако одна и та же сила вызывает различное ускорение у разных тел. Характеристикой инертности тела (т.е. сопротивления ускорению) служит его "масса", которую в первом приближении можно определить как "количество вещества": чем больше масса тела, тем меньше его ускорение под действием заданной силы. Таким образом, второй закон Ньютона утверждает, что ускорение тела пропорционально приложенной к нему силе и обратно пропорционально его массе. Если из наблюдений известны ускорение тела и его масса, то, используя этот закон, можно вычислить действующую на тело силу.

Закон противодействия. Этот закон утверждает, что взаимодействующие тела прилагают друг к другу равные по величине, но противоположно направленные силы. Поэтому в системе из двух тел, влияющих друг на друга одинаковой по величине силой, каждое испытывает ускорение, обратно пропорциональное его массе. Значит, лежащая на прямой между ними точка, удаленная от каждого обратно пропорционально его массе, будет двигаться без ускорения, несмотря на то, что каждое из тел движется ускоренно. Эту точку называют "центром масс"; вокруг нее обращаются звезды в двойной системе. Если одна из звезд вдвое массивнее другой, то она движется вдвое ближе к центру масс, чем ее соседка.

Законы Кеплера. Чтобы изучать движение небесных тел, познакомимся с силой гравитации. Лучше всего это сделать на примере взаимного движения двух тел: компонентов двойной звезды или Земли вокруг Солнца (для простоты предполагая, что другие планеты отсутствуют). К таким системам применимы законы Кеплера. В основе их лежит тот факт, что оба взаимодействующих тела движутся в одной плоскости. Это означает, что и сила гравитации всегда лежит в той же плоскости.

Закон эллипсов. Первый закон Кеплера утверждает, что планеты Солнечной системы движутся по эллипсам, в одном из фокусов которого находится Солнце. Фактически этот закон справедлив только для системы из двух тел, например для двойной звезды. Но и в Солнечной системе он выполняется довольно точно, поскольку на движение каждой планеты в основном влияет массивное Солнце, а все остальные тела влияют несравненно слабее.

Закон площадей. Если отмечать не только положение планеты, но и время, то можно узнать не только форму орбиты, но и характер движения планеты по ней. Оно подчиняется второму закону Кеплера, утверждающему, что линия, соединяющая Солнце и планету (или компоненты двойной звезды), за равные интервалы времени "заметает" равные площади. Например, эта линия между Солнцем и Землей каждые сутки заметает 2ґ1014 квадратных километров. Из закона площадей следует, что Солнце притягивает планету строго по прямой, соединяющей их центры. Верно и обратное: для любой центральной силы справедлив второй закон Кеплера. Рассмотрим планету (рис. 1), перемещающуюся из точки A в B за единицу времени. Если бы притяжение к точке O, где расположено Солнце, отсутствовало, то за следующую единицу времени планета переместилась бы в точку Y, такую, что AB = BY. С другой стороны, при наличии притяжения покоящееся в точке B тело переместилось бы за это время на расстояние x. Чтобы найти точку C, в которую действительно переместится планета, проведем прямую CY длиной x параллельно OB. Перпендикуляры, опущенные из точек Y и C на отрезок OB, очевидно, равны между собой. Если отрезок YD есть перпендикуляр из точки Y, а отрезок AE - перпендикуляр из точки A, то и они равны между собой из равенства треугольников YDB и AEB. Следовательно, высоты треугольников OBC и OBA равны, а значит, равны и площади этих треугольников, поскольку OB - их общее основание. Тем самым мы доказали, что за равные времена прямая, соединяющая планету с Солнцем (ее называют "радиусом-вектором" планеты), заметает равные площади. Если бы сила притяжения не была направлена точно к Солнцу, то отрезок CY не был бы параллелен прямой OB, и наше доказательство не было бы справедливым.

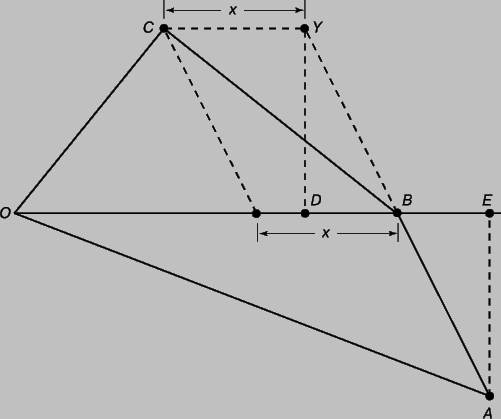
Рис. 1. ИЗ ЗАКОНА ПЛОЩАДЕЙ КЕПЛЕРА следует, что притяжение планеты и Солнца направлено строго по прямой линии между ними. Если Солнце расположено в точке O, а планета перемещается из B в C за то же время, что из A в B, то, согласно закону площадей, площади OBC и OBA равны между собой. Но это возможно в том и только в том случае, если притяжение Солнца направлено вдоль прямых OA, OB и OC.

Разумеется, приведенное выше доказательство справедливо лишь для бесконечно малых значений углов BOC и BOA. Однако любой отрезок орбиты можно представить как последовательность большого числа таких фигур, поэтому и для него доказательство останется справедливым.

Гармонический закон. Еще больше можно узнать о силе гравитации из третьего закона Кеплера, связывающего размер планетной орбиты с периодом обращения по ней. Его называют гармоническим законом, поскольку склонный к мистике Кеплер считал эту связь проявлением "небесной гармонии". Закон гласит, что если а - большая полуось эллиптической орбиты планеты, а P - период обращения по ней, то отношение a3/P2 одинаково для всех планет. Рассмотрим некоторую планету, обращающуюся вокруг Солнца по круговой орбите радиуса a. Солнце притягивает ее с постоянной по величине силой, сообщая ускорение, необходимое для равномерного изменения направления движения. Найдем это ускорение, вычислив изменение скорости планеты V за единицу времени (рис. 2). За период оборота планеты по орбите, равный 2pa/V, вектор скорости совершает полный поворот. Поэтому изменение скорости за это время равно длине окружности радиуса V. Изменение скорости за единицу времени, т.е. ускорение, составляет

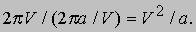
Обозначив орбитальный период через P, мы можем записать скорость как V = 2pa/Р. Тогда из выражения для ускорения получим, что оно пропорционально (a/P)2/a, или a/P2. Домножив числитель и знаменатель на a2, запишем это выражение так: (a3/P2)Ч(1/a2). Но, согласно гармоническому закону Кеплера, первый сомножитель постоянен - его значение одинаково для всех тел Солнечной системы. Значит, центростремительное ускорение и вызывающая его сила гравитации пропорциональны второму сомножителю, т.е. изменяются обратно пропорционально квадрату расстояния от Солнца. (Хотя мы доказали это только для круговой орбиты, более изощренные математические методы позволяют доказать это и для эллиптических орбит.)

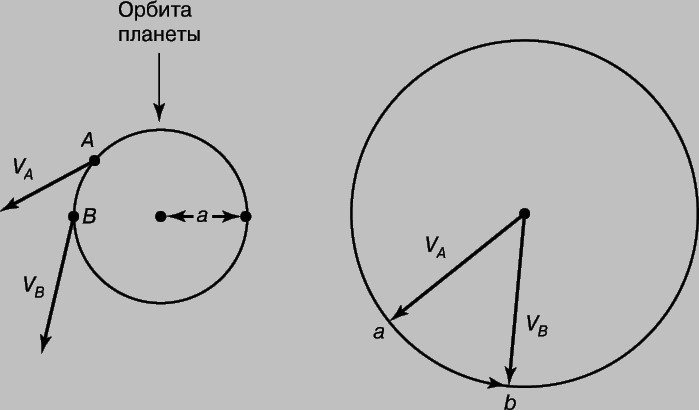
Рис. 2. ОПРЕДЕЛЕНИЕ СКОРОСТИ ИЗМЕНЕНИЯ НАПРАВЛЕНИЯ ДВИЖЕНИЯ ПЛАНЕТЫ ПО ОРБИТЕ. Слева показана планета на круговой орбите вокруг Солнца. В точках A и B скорость планеты представлена стрелками VA и VB. Изменение скорости при перемещении из A в B можно выразить дугой ab на окружности радиуса V (справа). При полном обороте планеты по орбите изменение скорости составит полную длину 2pV этой окружности.

Гармонический закон утверждает, что период обращения планеты зависит только от ее расстояния от Солнца и не зависит от ее массы. Значит, все тела, движущиеся по одной орбите, должны иметь одинаковую скорость.

Закон всемирного тяготения Ньютона. Анализируя законы Кеплера и наблюдательные данные о движении Луны, Ньютон сформулировал новый закон: каждая частица вещества притягивается к любой другой частице вдоль соединяющей их прямой с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними. Это всеобщий закон; он не ограничен влиянием Солнца на планеты. Он описывает также взаимодействие двух звезд, планеты и ее спутника, Земли и метеорита, Солнца и кометы. Все вещество во Вселенной подчиняется этому закону, поэтому его называют законом всемирного тяготения. Всеобщность этого закона дополняется его уникальностью: как доказали математики, планетные орбиты имеют вид эллипсов, в фокусе которых находится Солнце, только в том случае, если притяжение меняется обратно пропорционально квадрату расстояния. Казалось бы, попытка на основе ньютоновых законов движения и гравитации исследовать относительное движение взаимно притягивающихся тел должна привести к выводу знакомых нам законов Кеплера. Но это решительно не так, ибо законы Кеплера справедливы только в том случае, если: 1) взаимодействуют не более двух тел; 2) тела движутся по замкнутым орбитам; 3) масса одного из тел пренебрежимо мала по сравнению с массой другого. Эти условия делают анализ предельно простым, но они совершенно не обязательны для применения законов движения и гравитации. Используя эти общие законы, мы можем пренебречь указанными ограничениями. Сделаем это, отказываясь каждый раз лишь от одного из них. Во-первых, можно показать, что орбита может быть не только эллипсом (частный случай которого - окружность), но также параболой или гиперболой. Все эти кривые называют "коническими сечениями", поскольку они получаются при пересечении прямого кругового конуса плоскостью. Круг и эллипс - замкнутые кривые; парабола и гипербола - незамкнутые. Спутник, движущийся по замкнутой орбите, совершает одинаковые обороты снова и снова, а спутник, движущийся по незамкнутой кривой, приближается к главному телу с бесконечно далекого расстояния и, пролетев поблизости от него, вновь удаляется на бесконечность. Во-вторых, можно показать, что "постоянная" величина a3/P2 в гармоническом законе численно равна сумме масс двух взаимодействующих тел, если a выражено в расстояниях Земли от Солнца (в астрономических единицах), P - в периодах обращения Земли (в годах), а масса - в сумме масс Земли и Солнца. Поскольку в Солнечной системе масса любой планеты не превосходит тысячной доли массы Солнца, величины a3/P2 для всех планет различаются не более чем на 0,1%. Будь планеты массивнее, Кеплер не смог бы сформулировать свой гармонический закон. В общем виде этот закон выглядит так:

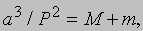
где M и m - массы компонентов системы, например Земли и Луны или звезд в двойной системе, причем значения масс могут быть любыми. (Все значения величин в этой формуле должны быть выражены в единой системе, например: астрономическая единица, год, масса Солнца.) Этот закон астрономы используют для определения масс различных космических объектов. Можно также исследовать поведение трех или более взаимно притягивающихся тел. Закон тяготения позволяет вычислить силу, действующую на каждое из тел со стороны остальных, а законы движения - определить, как изменяется от этого его скорость. В случае двух тел их траектории движения могут быть представлены простыми уравнениями Кеплера. Но если тел больше, то это невозможно сделать с помощью конечного числа уравнений. Этот последний случай наиболее часто встречается в небесной механике Солнечной системы. Важную проблему трех тел представляет система Земля - Луна - Солнце, но и здесь для точного вычисления орбиты Луны приходится учитывать возмущения со стороны других планет (особенно Юпитера и Сатурна), влияние экваториального вздутия Земли и даже влияние приливов, которые Луна вызывает в океанах Земли. Интерес к классической небесной механике значительно возрос в последние десятилетия в связи с необходимостью расчета орбит искусственных спутников и межпланетных аппаратов. Мощные компьютеры сделали возможным быстрое решение любой небесно-механической задачи с высокой точностью. Впервые для таких расчетов был использован компьютер SSEC фирмы IBM размером с комнату. Для вычисления положений Юпитера, Сатурна, Урана, Нептуна и Плутона с интервалом в 40 сут с 1653 по 2060 ему понадобилось 140 ч; сегодня рядовой компьютер делает это менее чем за 2 с. Теперь с помощью мощнейших компьютеров стало возможным решать такие задачи, которые были совершенно не доступны классической небесной механике: можно проследить на протяжении миллиардов лет эволюцию скопления, состоящего из сотен тысяч звезд; можно детально рассчитать, как исказится форма двух сталкивающихся галактик. Компьютер вдохнул новую жизнь в небесную механику.

Составить слова из слова небесная механика

сущ., кол-во синонимов: 3

комета, небесная скиталица, небесная странница

Составить слова из слова небесная пришелица

сущ., кол-во синонимов: 3

Составить слова из слова небесная скиталица

сущ., кол-во синонимов: 4

Составить слова из слова небесная странница

Небе́сная сфе́ра - воображаемая вспомогательная сфера произвольного радиуса, на которую проецируют небесные светила. Применяется в астрономии для изучения взаимного расположения и движения космических объектов на основе определения их координат на небесной сфере. На небесной сфере выделяют: большие круги (их центры совпадают с центром сферы); малые круги (их центры не лежат в центре сферы); математический горизонт; зенит; надир; точки Юг, Восток, Север и Запад; полюсы мира, небесный экватор и меридиан; эклиптику; точки солнцестояний и равноденствий; суточные параллели - малые круги, параллельные экватору, которые вследствие суточного вращения Земли описывают все небесные светила на небесной сфере.

* * *

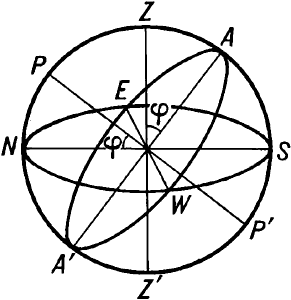
НЕБЕСНАЯ СФЕРА - НЕБЕ́СНАЯ СФЕ́РА, воображаемая вспомогательная сфера произвольного радиуса, на которую проецируют небесные светила. Применяется в астрономии для изучения взаимного расположения и движения космических объектов на основе определения их координат на небесной сфере. На небесной сфере выделяют: большие круги (их центры совпадают с центром сферы); малые круги (их центры не лежат в центре сферы); математический горизонт; зенит; надир; точки Юг, Восток, Север и Запад; полюсы мира, небесный экватор и меридиан; эклиптику; точки солнцестояний и равноденствий; суточные параллели - малые круги, параллельные экватору, которые вследствие суточного вращения Земли описывают все небесные светила на небесной сфере.

НЕБЕСНАЯ сфера - воображаемая вспомогательная сфера произвольного радиуса, на которую проецируют небесные светила. Применяется в астрономии для изучения взаимного расположения и движения космических объектов на основе определения их координат на небесной сфере. На небесной сфере выделяют: большие круги (их центры совпадают с центром сферы); малые круги (их центры не лежат в центре сферы); математический горизонт; зенит; надир; точки Юг, Восток, Север и Запад; полюсы мира, небесный экватор и меридиан; эклиптику; точки солнцестояний и равноденствий; суточные параллели - малые круги, параллельные экватору, которые вследствие суточного вращения Земли описывают все небесные светила на небесной сфере.

Когда мы наблюдаем небо, все астрономические объекты кажутся расположенными на куполообразной поверхности, в центре которой находится наблюдатель. Этот воображаемый купол образует верхнюю половину воображаемой сферы, которую называют "небесной сферой". Она играет фундаментальную роль при указании положения астрономических объектов.

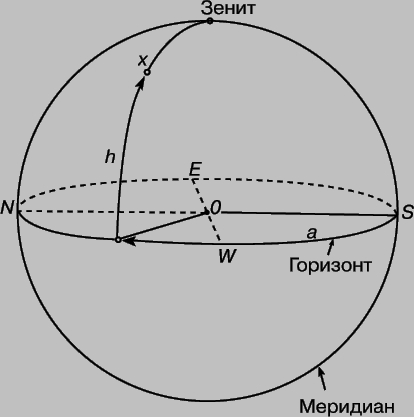
ДЛЯ УКАЗАНИЯ ПОЛОЖЕНИЙ ЗВЕЗД ИЛИ ДРУГИХ ТОЧЕК НА НЕБЕ астрономы используют понятие о небесной сфере - окружающей Землю воображаемой сфере, по которой происходит кажущееся движение светил. Один из методов указания положений дает альт-азимутальная (горизонтальная) система координат, в которой положение объекта определяется относительно горизонта или зенита (точка над головой наблюдателя, О) и относительно направления на юг (S). Положение звезды Х задается ее высотой (угловое расстояние от горизонта вдоль большого круга, проходящего через зенит) и азимутом а (измеренное к западу угловое расстояние от точки юга до точки горизонта, лежащей под звездой).

Хотя Луна, планеты, Солнце и звезды расположены на разных расстояниях от нас, даже самые близкие из них находятся так далеко, что мы не в состоянии на глаз оценить их удаленность. Направление на звезду не изменяется, когда мы перемещаемся по поверхности Земли. (Правда, оно немного изменяется при перемещении Земли по орбите, но заметить это параллактическое смещение можно лишь с помощью точнейших приборов.) Нам кажется, что небесная сфера вращается, поскольку светила восходят на востоке и заходят на западе.

Причиной этого служит вращение Земли с запада на восток. Кажущееся вращение небесной сферы происходит вокруг воображаемой оси, продолжающей земную ось вращения. Эта ось пересекает небесную сферу в двух точках, называемых северным и южным "полюсами мира". Северный полюс мира лежит примерно в градусе от Полярной звезды, а вблизи южного полюса нет ярких звезд.

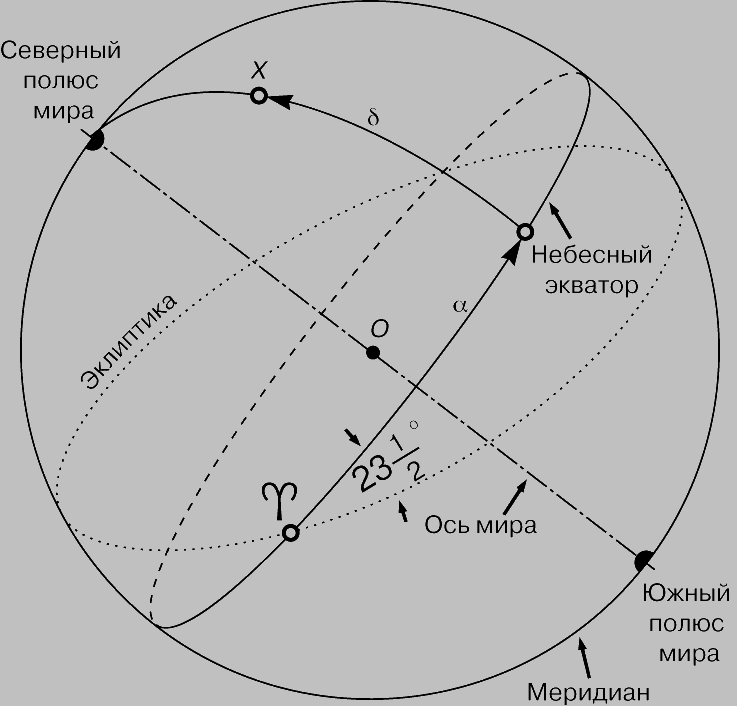
В ЭКВАТОРИАЛЬНОЙ СИСТЕМЕ положение звезды связано с небесным экватором (пересечение плоскости земного экватора с небесной сферой), северным и южным полюсами мира (точки пересечения земной оси с небесной сферой) и эклиптикой (видимый путь Солнца, пересекающего небесный экватор в марте в точке весеннего равноденствия, Положение звезды Х указывается ее прямым восхождением a (угловое расстояние вдоль небесного экватора от точки весеннего равноденствия до направления на звезду) и склонением d (угловое расстояние от небесного экватора вдоль большого круга, проходящего через полюсы мира).

Ось вращения Земли наклонена примерно на 23,5° относительно перпендикуляра, проведенного к плоскости земной орбиты (к плоскости эклиптики). Пересечение этой плоскости с небесной сферой дает круг - эклиптику, видимый путь Солнца за год. Ориентация земной оси в пространстве почти не изменяется. Поэтому каждый год в июне, когда северный конец оси наклонен в сторону Солнца, оно высоко поднимается на небе в Северном полушарии, где дни становятся длинными, а ночи короткими. Переместившись на противоположную сторону орбиты в декабре, Земля оказывается развернута к Солнцу Южным полушарием, и у нас на севере дни становятся короткими, а ночи - длинными.

См. также ВРЕМЕНА ГОДА. Однако под влиянием солнечного и лунного притяжения ориентация земной оси все же постепенно меняется. Основное движение оси, вызванное влиянием Солнца и Луны на экваториальное вздутие Земли, называют прецессией. В результате прецессии земная ось медленно поворачивается вокруг перпендикуляра к орбитальной плоскости, описывая за 26 тыс. лет конус радиусом 23,5°. По этой причине через несколько столетий полюс уже не будет вблизи Полярной звезды. Кроме того, ось Земли совершает мелкие колебания, называемые нутацией и связанные с эллиптичностью орбит Земли и Луны, а также с тем, что плоскость лунной орбиты немного наклонена к плоскости земной орбиты. Как мы уже знаем, вид небесной сферы в течение ночи меняется из-за вращения Земли вокруг оси. Но даже если наблюдать небо в одно и то же время в течение года, его вид будет меняться из-за обращения Земли вокруг Солнца. Для полного оборота по орбите на 360° Земле требуется ок. 3651/4 суток - примерно по градусу в сутки. Кстати, сутки, а точнее - солнечные сутки - это время, за которое Земля поворачивается один раз вокруг оси по отношению к Солнцу. Оно состоит из времени, за которое Земля совершает оборот по отношению к звездам ("звездные сутки"), плюс небольшое время - около четырех минут, - необходимое для поворота, компенсирующего орбитальное перемещение Земли за сутки на один градус. Таким образом, в году ок. 3651/4 солнечных суток и ок. 3661/4 звездных.

При наблюдении из определенной точки

Земли звезды, расположенные вблизи полюсов, либо всегда находятся над горизонтом, либо никогда не поднимаются над ним. Все остальные звезды восходят и заходят, причем каждый день восход и заход каждой звезды происходит на 4 мин раньше, чем в предыдущий день. Некоторые звезды и созвездия поднимаются на небе ночью в зимнее время - мы называем их "зимними", а другие - "летними". Таким образом, вид небесной сферы определяется тремя временами: временем суток, связанным с вращением Земли; временем года, связанным с обращением вокруг Солнца; эпохой, связанной с прецессией (хотя последний эффект едва ли заметишь "на глаз" даже за 100 лет).

Системы координат. Существуют различные способы для указания положения объектов на небесной сфере. Каждый из них подходит к задачам определенного типа.

Альт-азимутальная система. Для указания положения объекта на небе по отношению к окружающим наблюдателя земным предметам используют "альт-азимутальную", или "горизонтальную", систему координат. В ней указывают угловое расстояние объекта над горизонтом, называемое "высотой", а также его "азимут" - угловое расстояние вдоль горизонта от условной точки до точки, лежащей прямо под объектом. В астрономии азимут отсчитывают от точки юга к западу, а в геодезии и навигации - от точки севера к востоку. Поэтому, прежде чем пользоваться азимутом, нужно выяснить, в какой системе он указан. Точка неба, находящаяся прямо над головой, имеет высоту 90° и называется "зенит", а диаметрально противоположная ей точка (под ногами) - "надир". Для многих задач важен большой круг небесной сферы, называемый " небесным меридианом"; он проходит через зенит, надир и полюсы мира, а горизонт пересекает в точках севера и юга.

Экваториальная система. Из-за вращения Земли звезды постоянно перемещаются относительно горизонта и сторон света, а их координаты в горизонтальной системе изменяются. Но для некоторых задач астрономии система координат должна быть независимой от положения наблюдателя и времени суток. Такую систему называют "экваториальной"; ее координаты напоминают географические широты и долготы. В ней плоскость земного экватора, продолженная до пересечения с небесной сферой, задает основной круг - "небесный экватор". "Склонение" звезды напоминает широту и измеряется ее угловым расстоянием к северу или югу от небесного экватора. Если звезда видна точно в зените, то широта места наблюдения равна склонению звезды. Географической долготе соответствует "прямое восхождение" звезды. Оно измеряется к востоку от точки пересечения эклиптики с небесным экватором, которую Солнце проходит в марте, в день начала весны в Северном полушарии и осени - в Южном. Эту важную для астрономии точку называют "первой точкой Овна", или "точкой весеннего равноденствия", и обозначают знаком

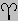
. Значения прямого восхождения обычно указывают в часах и минутах, считая 24 ч равными 360°. Экваториальную систему используют при наблюдении с телескопами. Телескоп устанавливают так, чтобы он мог вращаться с востока на запад вокруг оси, направленной на полюс мира, компенсируя этим вращение Земли.

Другие системы. Для некоторых целей используются и другие системы координат на небесной сфере. Например, когда изучают движение тел в Солнечной системе, используют систему координат, основной плоскостью которой служит плоскость земной орбиты. Строение Галактики изучают в системе координат, главной плоскостью которой служит экваториальная плоскость Галактики, представленная на небе кругом, проходящим вдоль Млечного Пути.

Сравнение систем координат. Важнейшие детали горизонтальной и экваториальной систем показаны на рисунках. В таблице эти системы сопоставлены с географической системой координат.

Переход из одной системы в другую. Часто возникает необходимость по альт-азимутальным координатам звезды вычислить ее экваториальные координаты, и наоборот. Для этого необходимо знать момент наблюдения и положение наблюдателя на Земле. Математически проблема решается с помощью сферического треугольника с вершинами в зените, северном полюсе мира и звезде Х; его называют "астрономическим треугольником". Угол с вершиной в северном полюсе мира между меридианом наблюдателя и направлением на какую-либо точку небесной сферы называют "часовым углом" этой точки; его измеряют к западу от меридиана. Часовой угол точки весеннего равноденствия, выраженный в часах, минутах и секундах, называют "звездным временем" (Si. T. - sidereal time ) в точке наблюдения. А поскольку прямое восхождение звезды - это тоже полярный угол между направлением на нее и на точку весеннего равноденствия, то звездное время равно прямому восхождению всех точек, лежащих на меридиане наблюдателя. Таким образом, часовой угол любой точки на небесной сфере равен разности звездного времени и ее прямого восхождения:

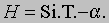
Пусть широта наблюдателя равна j. Если даны экваториальные координаты звезды a и d, то ее горизонтальные координаты а и можно вычислить по следующим формулам:

Можно решить и обратную задачу: по измеренным значениям а и h, зная время, вычислить a и d. Склонение d вычисляется прямо из последней формулы, затем из предпоследней вычисляется Н, а из первой, если известно звездное время, вычисляется a.

Представление небесной сферы. Многие столетия ученые искали наилучшие способы представления небесной сферы для ее изучения или демонстрации. Предлагались два типа моделей: двумерные и трехмерные. Небесную сферу можно изобразить на плоскости таким же образом, как сферическую Землю изображают на картах. В обоих случаях необходимо выбрать систему геометрической проекции. Первой попыткой представить участки небесной сферы на плоскости были наскальные рисунки звездных конфигураций в пещерах древних людей. В наши дни существуют различные звездные карты, изданные в виде рисованных или фотографических звездных атласов, покрывающих все небо. Древние китайские и греческие астрономы представляли небесную сферу в виде модели, известной как "армиллярная сфера". Она состоит из металлических кругов или колец, соединенных вместе так, чтобы показать важнейшие круги небесной сферы. Сейчас нередко используют звездные глобусы, на которых отмечены положения звезд и основных кругов небесной сферы. У армиллярных сфер и глобусов есть общий недостаток: положение звезд и разметка кругов нанесены на их внешней, выпуклой стороне, которую мы рассматриваем снаружи, тогда как на небо мы смотрим "изнутри", и звезды нам кажутся размещенными на вогнутой стороне небесной сферы. Это иногда приводит к путанице направлений движения звезд и фигур созвездий. Наиболее реалистическое представление небесной сферы дает планетарий. Оптическая проекция звезд на полусферический экран изнутри позволяет очень точно воспроизвести вид неба и всевозможные движения светил на нем.

См. также

АСТРОНОМИЯ И АСТРОФИЗИКА;

ПЛАНЕТАРИЙ;

ЗВЕЗДЫ.

Составить слова из слова небесная сфера

Устар. Поэт. Небо. [Ломоносов] в первых летах юношества был сильно поражён… солнцем, которое в ближайшие дни лета, дошед до горизонта, снова восстаёт и снова течёт по небесной тверди (Батюшков. Нечто о поэте).

О ты, что свыше круга звездна Сидишь, царей суды внемля, Трон коего есть твердь небесна, А ног подножие земля! (Крылов. Ода на заключение мира…).

сущ., кол-во синонимов: 7

Составить слова из слова небесная твердь