▲ трансцендентная функция

↑ угол

синус. косинус. тангенс. котангенс. секанс. косеканс. арксинус. арккосинус.

синусоида. тангенсоида.

Составить слова из слова тригонометрическая функция

Тригонометри́ческие фу́нкции - функции угла: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), секанс (sec), косеканс (cosec). Их можно определить как отношения длины r и проекций а и b на оси координат радиуса-вектора, образующего с положительным направлением оси Ох угол (или отсекающего дугу) α (рис. 1).

Именно:

, ,

, , .

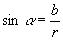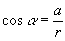
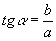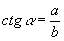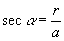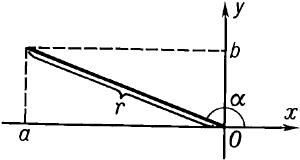
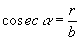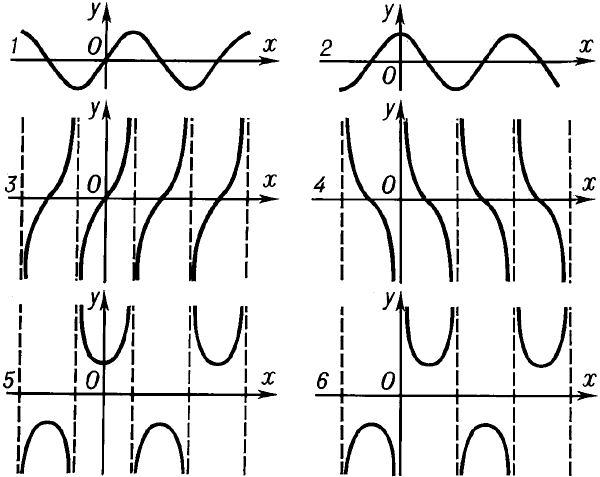
Значения тригонометрических функций для различных углов даются в таблицах; графики тригонометрических функций см. на рис. 2 (1 - синус, 2 - косинус, 3 - тангенс, 4 - котангенс, 5 - секанс, 6 - косеканс). Тригонометрические функции играют важнейшую роль в математике.

* * *

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ - ТРИГОНОМЕТРИ́ЧЕСКИЕ ФУ́НКЦИИ, функции угла: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), секанс (sec), косеканс (cosec).

Их можно определить как отношения длины r и проекций а и b на оси координат радиуса-вектора, образующего с положительным направлением оси Ох угол (или отсекающего дугу) a. Именно: sin a=^b/_r, cos a=^a/_r, tg a=^b/_a, сtg a=^a/_b, sec a=^r/_а, cosec a=^r/_b. Играют важнейшую роль в математике.

ТРИГОНОМЕТРИЧЕСКИЕ функции - функции угла: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), секанс (sec), косеканс (cosec). Их можно определить как отношения длины r и проекций а и b на оси координат радиуса-вектора, образующего с положительным направлением оси Ох угол (или отсекающего дугу) ?. Именно: sin ?=b/r, cos ?=a/r, tg ?=b/a, сtg ?=a/b, sec ?=r/а, cosec ?=r/b. Играют важнейшую роль в математике.

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ (от греческого trigonon - треугольник и функция), функции угла. Таковы, например, синус (sin a), косинус (cos a), тангенс (tg a), котангенс (ctg a). Они выражают отношения длин сторон прямоугольного треугольника. Например, sin a - отношение длины одного из катетов треугольника к длине его гипотенузы.

Составить слова из слова тригонометрические функции

прил.

1. соотн. с сущ. тригонометрия, связанный с ним

2. Свойственный тригонометрии, характерный для неё.

3. Принадлежащий тригонометрии.

ТРИГОНОМЕТРИ́ЧЕСКИЙ, тригонометрическая, тригонометрическое (мат.). прил. к тригонометрия.

ТРИГОНОМЕ́ТРИЯ, -и, ж. Раздел математики, изучающий соотношения между сторонами и углами треугольника.

-ая, -ое.

1. прил. к тригонометрия.

Тригонометрические таблицы.

2. геод.

Связанный с геодезическими измерениями, производимыми методом триангуляции (во 2 знач.).

Тригонометрический знак. Тригонометрический пункт.

◊

тригонометрические функции

мат.

функции угла: синус, косинус, тангенс, котангенс, секанс, косеканс.

тригонометри́ческий

тригонометри́ческий, тригонометри́ческая, тригонометри́ческое, тригонометри́ческие, тригонометри́ческого, тригонометри́ческой, тригонометри́ческих, тригонометри́ческому, тригонометри́ческим, тригонометри́ческую, тригонометри́ческою, тригонометри́ческими, тригонометри́ческом, тригонометри́ческ, тригонометри́ческа, тригонометри́ческо, тригонометри́чески

прил., кол-во синонимов: 2

триангуляционный, геодезический

тр/и/гон/о/метр/и́ческ/ий.

тригонометри́ческий п 3a✕~

ТРИГОНОМЕТРИЧЕСКИЙ ая, ое. trigonométrique adj. Отн. к тригонометрии, основанный на тригонометрии. БАС-1. Сектор или пропорциональный циркуль; есть орудие из двух пальмового дерева или кости, медных, либо серебреных линеек, двумя концами своими соединенных имеет шарньером, и свободно около цилиндрического гвоздика, как центра, движущихся. Орудие сие употребляется для решения геометрических и тригонометрических задач. Ян. 1806. Я уже полагал, что на меня наброшена тригометрическая <так> сеть и что я никогда не свяжу узлов в мою пользу. 1831. Маевский Мой век. // РС 1873 8 151. ♦ Тригонометрический пункт. Геодезический пункт, положение которого на местности определено методом триангуляции. БАС-1.♦ Тригонометрический знак, т. вышка и т. п. Сооружение, устанавливаемое на местности в геодезическом опорном пункте. БАС-1. - Лекс. САР 1794: тригонометри/ческий.

К тригонометрии относящейся, ей принадлежащий или на ней основанный.

Составить слова из слова тригонометрический

Тригонометри́ческий пункт (триангуляционный пункт), геодезический пункт, координаты которого получены триангуляцией; положение на местности обозначается деревянным или металлическим сооружением в виде пирамиды.

* * *

ТРИГОНОМЕТРИЧЕСКИЙ ПУНКТ - ТРИГОНОМЕТРИ́ЧЕСКИЙ ПУНКТ (триангуляционный пункт), геодезический пункт (см. ГЕОДЕЗИЧЕСКИЙ ПУНКТ) , координаты которого получены триангуляцией (см. ТРИАНГУЛЯЦИЯ); положение на местности обозначается деревянным или металлическим сооружением в виде пирамиды.

ТРИГОНОМЕТРИЧЕСКИЙ пункт (триангуляционный пункт) - геодезический пункт, координаты которого получены триангуляцией; положение на местности обозначается деревянным или металлическим сооружением в виде пирамиды.

Составить слова из слова тригонометрический пункт

Тригонометри́ческий ряд - ряд вида

,

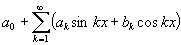где коэффициент а₀, a₁, b₁, a₂, b₂, ... не зависят от переменного х.

* * *

ТРИГОНОМЕТРИЧЕСКИЙ РЯД - ТРИГОНОМЕТРИ́ЧЕСКИЙ РЯД, ряд вида , где коэффициенты a₀, а₁, b₁, а₂, b₂ ... не зависят от переменного х.

ТРИГОНОМЕТРИЧЕСКИЙ ряд - ряд вида , где коэффициенты a0, а1, b1, а2, b2 ... не зависят от переменного х.

Составить слова из слова тригонометрический ряд

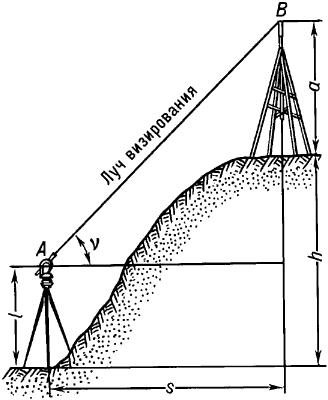
Тригонометри́ческое (геодези́ческое) нивели́рование - метод определения превышений (h) по измеренному теодолитом (кипрегелем, эклиметром) углу наклона линии визирования (v) с одной точки (А) на другую (В) и расстоянию (s) между этими точками: h = stgv + l-a, где l - высота прибора, a - высота цели. Применяется при топографической съёмке и других работах.

* * *

ТРИГОНОМЕТРИЧЕСКОЕ (ГЕОДЕЗИЧЕСКОЕ) НИВЕЛИРОВАНИЕ - ТРИГОНОМЕТРИ́ЧЕСКОЕ (ГЕОДЕЗИ́ЧЕСКОЕ) НИВЕЛИ́РОВАНИЕ, метод определения превышений (h) по измеренному теодолитом (см. ТЕОДОЛИТ) (кипрегелем (см. КИПРЕГЕЛЬ), эклиметром (см. ЭКЛИМЕТР) ) углу наклона линии визирования (v) с одной точки (А) на другую (В) и расстоянию (s) между этими точками: h=s·tgv + l - a, где l - высота прибора, а - высота цели. Применяется при топографической съемке (см. ТОПОГРАФИЧЕСКАЯ СЪЕМКА) и других работах.

Составить слова из слова тригонометрическое (геодезическое) нивелирование

ТРИГОНОМЕТРИЧЕСКОЕ (ГЕОДЕЗИЧЕСКОЕ) НИВЕЛИРОВАНИЕ - метод определения превышений (h) по измеренному теодолитом (кипрегелем, эклиметром) углу наклона линии визирования (?) с одной точки (А) на другую (В) и расстоянию (s) между этими точками: h=s.tg? + l - a, где l - высота прибора, а - высота цели. Применяется при топографической съемке и других работах.

Составить слова из слова тригонометрическое нивелирование

Тригонометри́ческое уравне́ние - уравнение, содержащее тригонометрические функции неизвестного аргумента, например: 3sin х-8cos х = 7.

* * *

ТРИГОНОМЕТРИЧЕСКОЕ УРАВНЕНИЕ - ТРИГОНОМЕТРИ́ЧЕСКОЕ УРАВНЕ́НИЕ, уравнение, содержащее тригонометрические функции неизвестного аргумента, напр.: 3sinx-8cosx =7.

ТРИГОНОМЕТРИЧЕСКОЕ уравнение - уравнение, содержащее тригонометрические функции неизвестного аргумента, напр.: 3sinx-8cosx =7.

Составить слова из слова тригонометрическое уравнение

ж.

Раздел математики, изучающий тригонометрические функции и их применение к решению задач.

ТРИГОНОМЕ́ТРИЯ, тригонометрии, мн. нет, жен. (от греч. trigonos - треугольник и metreo - мерю) (мат.). Отдел геометрии о соотношениях между сторонами и углами треугольника.

ТРИГОНОМЕ́ТРИЯ, -и, жен. Раздел математики, изучающий соотношения между сторонами и углами треугольника.

| прил. тригонометрический, -ая, -ое.

ТРИГОНОМЕТРИЯ - греч. математика треугольников; наука вычислять что с помощью построения треугольников. -трическая съемка и триангуляция, съемка местности по тригонометрии.

ТРИГОНОМЕ́ТРИЯ -и; ж. [от греч. trigōnon - треугольник и metreō - измеряю] Раздел математики, изучающий функции угла (синус, косинус, тангенс, котангенс, секанс, косеканс) и их приложения к геометрии. Прямолинейная т. Сдать зачёт по тригонометрии.

◁ Тригонометри́ческий, -ая, -ое. Т-ие функции. Т-ое уравнение.

* * *

тригономе́трия (от греч. trígōnon - треугольник и ...метрия), раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии.

* * *

ТРИГОНОМЕТРИЯ - ТРИГОНОМЕ́ТРИЯ (от греч. trigonon - треугольник и metreo - измеряю), раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии.

ТРИГОНОМЕТРИЯ (от греч. trigonon - треугольник и ...метрия) - раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии.

-и, ж.

Раздел математики, изучающий тригонометрические функции и их приложения к геометрии.

Прямолинейная тригонометрия. Сферическая тригонометрия.

[От греч. τρίγωνον - треугольник и μετρέω - мерю]

ТРИГОНОМЕТРИЯ (от греческого trigonon - треугольник и ...метрия), раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии. Отдельные задачи тригонометрии решались астрономами Древней Греции (3 в. до нашей эры); систематическое развитие тригонометрии в средние века осуществлено среднеазиатскими учеными. Современный вид тригонометрия получила у Л. Эйлера (18 в.).

тригономе/трия, -и

тригономе́трия, -и

тригономе́трия, -и

тригономе́трия, тригономе́трии, тригономе́трий, тригономе́триям, тригономе́трию, тригономе́трией, тригономе́триею, тригономе́триями, тригономе́триях

тр/и/гон/о/ме́тр/и/я [й/а].

тригономе́трия ж 7a

Заимств. в XVIII в. из ученой латыни, где trigonometria - сложение греч. trigōnon «треугольник» и metreō «измеряю». См. метр.

ТРИГОНОМЕТРИЯ и, ж. trigonométrie f. <гр. trigonon треугольник + metreo меряю. Отдел геометрии о соотношениях между сторонами и углами треугольника. БАС-1. Началась корпусная комиссия, и я екзаменовался.. Из Арифметики, Геометрии, Тригонометрии плоской и сверической. Навигации, Астрономии, Еволюции и Практики и был отмечен из всего хорошо. 1814. Вл. Романов Дн. // ЩС 2 157. - Лекс. САР 1794: тригономе/триа; САР 1822: тригономе/трия.

ТРИГОНОМЕТРИЯ (греч., от tri, gonia - угол, и metron - мера). Часть математики, занимающаяся измерением треугольников.

- Какое известное нам со школы слово начинается на три Г, а кончается на три Я?

- Раздел математики, изучающий треугольники.

- Первый учебник этой науки принадлежит Региомонтану и называется «Пять книг о треугольниках всех видов».

- Название этого раздела математики в переводе с греческого означает «измерение треугольников».

Составить слова из слова тригонометрия