ж.

Кривая, описываемая фиксированной точкой окружности, катящейся без скольжения по неподвижной прямой (в математике).

ЦИКЛО́ИДА, циклоиды, жен., (греч. kykloeidos - кругообразный) (мат.). Кривая линия, описываемая точкой окружности, которая катится без скольжения по прямой линии.

ЦИКЛО́ИДА -ы; ж. [греч. kykloeides - кругообразный от kyklos - круг и eidos - вид] Матем. Плоская кривая, описываемая фиксированной точкой окружности, катящейся без скольжения по неподвижной прямой.

* * *

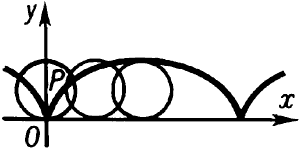
цикло́ида (от греч. kykloeidēs - кругообразный), плоская кривая (рис.), описываемая точкой Р окружности, катящейся без скольжения по неподвижной прямой. Циклоида - трансцендентная кривая. См. также Гипоциклоида, Эпициклоида.

* * *

ЦИКЛОИДА - ЦИКЛО́ИДА (от греч. kykloeides - кругообразный), плоская кривая, описываемая точкой Р окружности, катящейся без скольжения по неподвижной прямой. Циклоида - трансцендентная кривая. См. также Гипоциклоида (см. ГИПОЦИКЛОИДА), Эпициклоида (см. ЭПИЦИКЛОИДА).

ЦИКЛОИДА (от греч. kykloeides - кругообразный) - плоская кривая, описываемая точкой Р окружности, катящейся без скольжения по неподвижной прямой. Циклоида - трансцендентная кривая. См. также Гипоциклоида, Эпициклоида.

-ы, ж. мат.

Плоская кривая, описываемая фиксированной точкой окружности, катящейся без скольжения по неподвижной прямой.

[От греч. κυκλοειδής - кругообразный]

Гипоциклоида.

ЦИКЛОИДА (от греческого kykloeides - кругообразный), плоская кривая, описываемая точкой окружности, катящейся без скольжения по неподвижной прямой. Если кривая описывается точкой окружности, которая катится без скольжения по неподвижной окружности внутри ее, то кривая называется гипоциклоидой, вне ее - эпициклоидой.

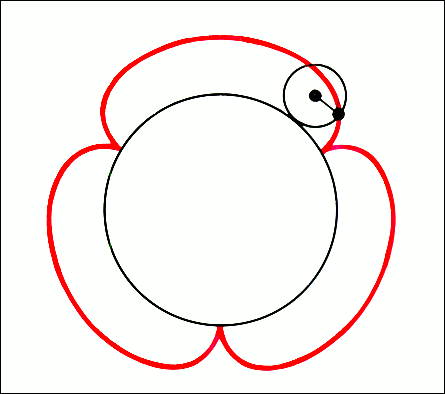
Эпициклоида.

Циклоида.

цикло́ида, -ы

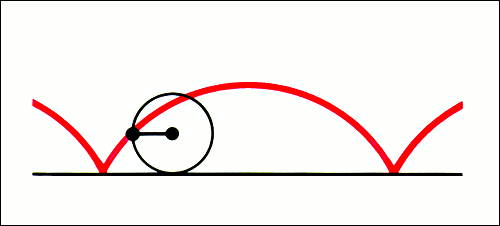
цикло́ида

цикло́ида, цикло́иды, цикло́ид, цикло́иде, цикло́идам, цикло́иду, цикло́идой, цикло́идою, цикло́идами, цикло́идах

сущ., кол-во синонимов: 2

цикл/о́ид/а.

цикло́ида ж 1a

ЦИКЛОИДА ы, ж. cycloïde <гр. kykloeides кругообразный. геом. Плоская кривая, описываемая точкой окружности, катящейся без скольжения по прямой. БАС-1. Поэтический полет определен циклоидой. В. Ф. Одоевский Импровизатор. Эллипс имеет не те качества, какие гипербола, или циклоида, или синусоида. 8. 3. 1878. Черныш. - А. Н. и Т. Н. Чернышевским. Цикло/идный, циклоида/льный. Крысин 1998. - Лекс. Ян. 1806: циклоида; Даль-3: цикло/ида; СИС 1937: цикло/ида; Михельсон 1866: циклоидальный; СИС 1937: циклоида/льный.

ЦИКЛОИДА (греч., от kyklos - круг, и eidos - вид). В геометрии, кривая, описываемая точкою круга, катящегося по прямой линии; кривообразная линия.

- Кривая, описываемая точкой окружности.

- Название этой плоской кривой в переводе с греческого означает «кругообразная».

- В какую кривую превратится брахистохрона при отсутствия сопротивления среды.

- Плоская кривая, описываемая точкой Р окружности, катящейся без скольжения по неподвижной прямой.

Составить слова из слова циклоида

прил.

1. соотн. с сущ. циклоида, связанный с ним

2. Имеющий форму циклоиды.

ЦИКЛОИДА́ЛЬНЫЙ, циклоидальная, циклоидальное (мат.). Имеющий форму циклоиды. Циклоидальная линия.

ЦИКЛОИДА́ЛЬНЫЙ -ая, -ое. Спец. Имеющий форму циклоиды. Ц-ая линия.

-ая, -ое. спец.

Имеющий форму циклоиды.

Циклоидальная линия.

циклоида́льный

циклоида́льный

циклоида́льный, циклоида́льная, циклоида́льное, циклоида́льные, циклоида́льного, циклоида́льной, циклоида́льных, циклоида́льному, циклоида́льным, циклоида́льную, циклоида́льною, циклоида́льными, циклоида́льном, циклоида́лен, циклоида́льна, циклоида́льно, циклоида́льны, циклоида́льнее, поциклоида́льнее, циклоида́льней, поциклоида́льней

прил., кол-во синонимов: 1

цикл/оид/а́льн/ый.

циклоида́льный п 1*a

Имеющий форму циклоиды.

Составить слова из слова циклоидальный