м.

Алгебраическое выражение, представляющее сумму или разность двух одночленов; двучлен (в математике).

БИНО́М, -а, муж. В математике: двучлен.

БИНОМ - муж. биномия жен. в буквосчислении: численное выражение, состоящее из двух членов; двучлен, двучленная величина.

БИНО́М -а; м. [от лат. bis - дважды и греч. nomē - часть, доля] Матем. Алгебраическое выражение, представляющее сумму или разность двух одночленов; двучлен.

* * *

бино́м (от би... и лат. nomen - имя), то же, что двучлен. О биноме вида (х + y)ⁿ см. Ньютона бином.

* * *

БИНОМ - БИНО́М (от лат. bi - дву(х)- и лат. nomen - имя), то же, что двучлен (см. ДВУЧЛЕН). О биноме вида (x+y)ⁿ смотри в статье Ньютона бином (см. НЬЮТОНА БИНОМ).

БИНОМ (от би... и лат. nomen - имя) - то же, что двучлен. О биноме вида (x+y)n см. в ст. Ньютона бином.

-а, м. мат.

Алгебраическое выражение, представляющее сумму иди разность двух одночленов; двучлен.

[От лат. bis - дважды и греч. νόμος - часть, отдел]

БИНОМ (от би... и латинского nomen - имя) (двучлен), алгебраическая сумма двух одночленов.

Бином Ньютона. Разг. Шутл. О чём-л. сложном, запутанном. Елистратов, 41.

БИНОМ, -а, м. (или бином ньютона). Ирон.

О чем-л. кажущемся сложным, запутанным.

Возм. распространилось под влиянием романа М. Булгакова «Мастер и Маргарита».

бино́м, -а

бино́м

бино́м, бино́мы, бино́ма, бино́мов, бино́му, бино́мам, бино́мом, бино́мами, бино́ме, бино́мах

сущ., кол-во синонимов: 1

двучлен

сущ.

двучлен

би/но́м/ [ср.: мо(но)/ном/, поли/ном/].

бино́м м 1a

Заимств. в первой половине XIX в. из франц. яз., где binôme - сложение лат. bi (< bis «двое, дважды») и греч. nomē «часть, доля». Ср. словообразовательную кальку этого слова - двучлен.

бино́м

матем., из франц. binôme или из нем. Binom от лат. bi- "двух-" и греч. νόμος "закон".

БИНОМ а, м. binôme, лат. binomia m.

1. мат. Алгебраическое выражение, представляющее сумму или разность одночленов; двучлен. БАС-2. Боюсь, еслиб я и осмелился представить здесь самое простое развитие двучленника (бинома) Ньютонова необходимого для сего исчисления. Совр. 1836 3 31. Каким Дон-Кихотом должен показаться в этой девственной атмосфере <невежества> злоухищренный бином с его коэффициентами, экспонентами и удвоенными произведениями. 1877. Е. Марков Сомнения в школьной практике. // М. 2 475. Прошла зима, я допер до бинома Ньютона, сдал экзамены и получил вожделенный аттестат зрелости. А. Генатулин Что там за холмом? // ДН 2000 8 97. ♦ Подумаешь, бином Ньютона. Булгаков Мастер и Маргарита. // Душенко 57. "Сложный вопрос" - подумаешь бином Ньютона. ДН 2002 1 127. Подумаешь бином Ньютона! Дело в истории обыкновенное, волноваться не о чем! Звезда 2004 4 210. || Сейчас, надеюсь, временно, оппозиция "Север-Юг" имеет параллель биному "богатство- бедность". Звезда 2001 1 220.

2. шутл., студ. Студент факультета информатики. Попроси биномов. они тебе все решат на перемене. Запись 1998. Никитина 1998. Биномиальный ая, ое. binômial,-e adj. Двойная (биномиальная) номенклатура видов. Вагнер. 152. Коренблит 1934 1 361. Биномный ая, ое. Биномный ряд. Коренблит 1934 1 361. - Лекс. Энц. Лекс. 1836: бином; САН 1847: бино/м; Сл. 18: бином 1798, бинома 1752.

БИНОМ (от лат. bis - дважды, и греч. nomos - часть, отдел). Двучлен (в алгебре). - Бином Ньютона - общая формула для возведения двучленного количества в любую степень.

- Математический двучлен.

- Подумаешь, у Ньютона!

Составить слова из слова бином

Разг. Шутл. О чём-л. сложном, запутанном. Елистратов, 41.

БИНОМ, -а, м. (или бином ньютона). Ирон.

О чем-л. кажущемся сложным, запутанным.

Возм. распространилось под влиянием романа М. Булгакова «Мастер и Маргарита».

Составить слова из слова бином ньютона

Биномиа́льное распределе́ние (распределение Бернулли), распределение вероятностей числа появлений некоторого события при повторных независимых испытаниях, если вероятность появления этого события в каждом испытании равна р (0≤р≤1). Именно, число μ появлений этого события есть случайная величина, принимающая значения m = 0, 1, 2, ..., n с вероятностями 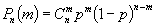, где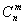 - биномиальные коэффициенты (см. Ньютона бином).

* * *

БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ - БИНОМИА́ЛЬНОЕ РАСПРЕДЕЛЕ́НИЕ (распределение Бернулли), распределение вероятностей числа появлений некоторого события при повторных независимых испытаниях, если вероятность появления этого события в каждом испытании равна p ( p больше или равно 0, меньше или равно 1). Именно, число m появлений этого события есть случайная величина, принимающая значения m = 0, 1, 2, ..., n с вероятностями P_n(m) = Cp^m(1-p)^n-m, где C - биномиальные коэффициенты (см. Ньютона бином (см. НЬЮТОНА БИНОМ)).

БИНОМИАЛЬНОЕ распределение (распределение Бернулли) - распределение вероятностей числа появлений некоторого события при повторных независимых испытаниях, если вероятность появления этого события в каждом испытании равна p(0"p"1). Именно, число ? появлений этого события есть случайная величина, принимающая значения m - 0, 1, 2, ..., n с вероятностями Pn(m) = Cpm(1-p)n-m, где C - биномиальные коэффициенты (см. Ньютона бином).

Составить слова из слова биномиальное распределение

биномиа́льный

биномиа́льный, биномиа́льная, биномиа́льное, биномиа́льные, биномиа́льного, биномиа́льной, биномиа́льных, биномиа́льному, биномиа́льным, биномиа́льную, биномиа́льною, биномиа́льными, биномиа́льном, биномиа́лен, биномиа́льна, биномиа́льно, биномиа́льны, биномиа́льнее, побиномиа́льнее, биномиа́льней, побиномиа́льней

прил., кол-во синонимов: 2

двучленный, биноминальный

би/ном/и/а́льн/ый.

биномиа́льный п 1*a

биномиа́льный

- мат. относящийся к биному; б-ые коэффициенты - коэффициенты в разложении бинома ньютона.

Составить слова из слова биномиальный

Биномиа́льный коэффицие́нт - коэффициент в формуле разложения Ньютона бинома.

* * *

БИНОМИАЛЬНЫЙ КОЭФФИЦИЕНТ - БИНОМИА́ЛЬНЫЙ КОЭФФИЦИЕ́НТ, коэффициент в формуле разложения Ньютона бинома (см. НЬЮТОНА БИНОМ).

БИНОМИАЛЬНЫЙ коэффициент - коэффициент в формуле разложения Ньютона бинома.

Составить слова из слова биномиальный коэффициент

Биномиа́льный ряд - бесконечный степенной ряд, являющийся обобщением формулы Ньютона бинома на случай дробных и отрицательных показателей.

* * *

БИНОМИАЛЬНЫЙ РЯД - БИНОМИА́ЛЬНЫЙ РЯД, бесконечный степенной ряд, являющийся обобщением формулы Ньютона бинома (см. НЬЮТОНА БИНОМ) на случай дробных и отрицательных показателей.

БИНОМИАЛЬНЫЙ РЯД - бесконечный степенной ряд, являющийся обобщением формулы Ньютона бинома на случай дробных и отрицательных показателей.

Составить слова из слова биномиальный ряд

биномина́льный, биномина́льная, биномина́льное, биномина́льные, биномина́льного, биномина́льной, биномина́льных, биномина́льному, биномина́льным, биномина́льную, биномина́льною, биномина́льными, биномина́льном, биномина́лен, биномина́льна, биномина́льно, биномина́льны, биномина́льнее, побиномина́льнее, биномина́льней, побиномина́льней

прил., кол-во синонимов: 2

Коэффициент в разложении степени (о числах).

Составить слова из слова биноминальный

прил., кол-во синонимов: 1

БИНОМНЫЙ (этим. см. Бином). Двучленный (говорится о математических формулах).

Составить слова из слова биномный