прил., кол-во синонимов: 7

Составить слова из слова проиллюстрировавший

проиллюстри́рованный; кратк. форма -ан, -ана

проиллюстри́рованный, -ан, -ана, -ано, -аны

прил., кол-во синонимов: 5

про/иллюстр/и́р/ова/нн/ый.

Составить слова из слова проиллюстрированный

сов. перех.

1. Снабдить текст рисунками, иллюстрациями.

2. Снабдить изложение, рассуждение и т.п. материалами, способствующими их пониманию.

ПРОИЛЛЮСТРИ́РОВАТЬ см. иллюстрировать.

ПРОИЛЛЮСТРИ́РОВАТЬ -рую, -руешь; св. (нсв. иллюстри́ровать). что.

1. Снабдить (текст) рисунками, иллюстрациями. П. книгу, рассказ.

2. Снабдить изложение, рассуждение и т.п. материалами, способствующими их наглядности. П. лекцию слайдами. П. свою мысль примерами. П. наблюдение историческими фактами.

-рую, -руешь.

сов. к иллюстрировать.

проиллюстри́ровать, -рую, -рует

проиллюстри́ровать, -ри́рую, -ри́руешь

проиллюстри́ровать, проиллюстри́рую, проиллюстри́руем, проиллюстри́руешь, проиллюстри́руете, проиллюстри́рует, проиллюстри́руют, проиллюстри́руя, проиллюстри́ровал, проиллюстри́ровала, проиллюстри́ровало, проиллюстри́ровали, проиллюстри́руй, проиллюстри́руйте, проиллюстри́ровавший, проиллюстри́ровавшая, проиллюстри́ровавшее, проиллюстри́ровавшие, проиллюстри́ровавшего, проиллюстри́ровавшей, проиллюстри́ровавших, проиллюстри́ровавшему, проиллюстри́ровавшим, проиллюстри́ровавшую, проиллюстри́ровавшею, проиллюстри́ровавшими, проиллюстри́ровавшем, проиллюстри́рованный, проиллюстри́рованная, проиллюстри́рованное, проиллюстри́рованные, проиллюстри́рованного, проиллюстри́рованной, проиллюстри́рованных, проиллюстри́рованному, проиллюстри́рованным, проиллюстри́рованную, проиллюстри́рованною, проиллюстри́рованными, проиллюстри́рованном, проиллюстри́рован, проиллюстри́рована, проиллюстри́ровано, проиллюстри́рованы

см. пояснить

отыллюстрировать, иллюстрировать, растолковать, объяснить, пояснить

про/иллюстр/и́р/ова/ть.

проиллюстри́ровать св 2a

Составить слова из слова проиллюстрировать

АНТЕННА - конструкция, используемая для передачи или приема радиоволн (т.е. электромагнитных излучений с длинами волн в пределах от АНТЕННА20 000 м до АНТЕННА1 мм). В качестве примеров использования антенн можно привести радио и телевещание, дальнюю радиосвязь на коротких волнах и микроволнах, отраженных спутниковыми антеннами, радиолокацию - в основе всех этих физических процессов и технических систем лежит передача энергии в форме электромагнитных волн через воздушное и космическое пространство. Функция передающей антенны состоит в том, чтобы преобразовывать электромагнитную энергию, поступающую от передатчика, в излучаемую электромагнитную волну. На стороне приема тоже необходимо иметь антенну, которая принимает часть энергии, излученной передающей антенной, и пересылает ее на более или менее сложные детектирующие и усиливающие схемы, которые и составляют основу приемника.

См. РАДИО И ТЕЛЕВИДЕНИЕ; РАДИОЛОКАЦИЯ.

ТИПЫ АНТЕНН

Тип конструкции антенны зависит от длины волн, на которых она должна работать. Чтобы эффективно излучать энергию, антенна должна иметь размеры, близкие к длине рабочей волны. Поэтому на низких частотах, использовавшихся в свое время для трансатлантической радиотелеграфной и радиотелефонной связи (частоты от 16 до 70 кГц, т.е. волны длиной от 19 до 4,3 км), огромная система антенных проводов общей протяженностью до 2 км представляла собой электрически короткую антенну и оказывалась, следовательно, неэффективным излучателем. Если такая антенна должна была иметь заметную направленность, то ее эффективность получалась очень низкой. Напротив, на сверхвысоких частотах (СВЧ) использование полуволнового симметричного вибратора длиной менее 1 см и отполированного металлического рефлектора диаметром всего лишь несколько сантиметров позволяет весьма эффективно фокусировать излучение такого вибратора в узкий луч.

АНТЕННЫ ДЛЯ РАДИОВЕЩАНИЯ С АМПЛИТУДНОЙ МОДУЛЯЦИЕЙ (540-1600 кГц, 550-190 м)

Четвертьволновая передающая антенная мачта. Основная зона охвата широковещательной станции "обслуживается" поверхностной (земной) волной. Для того чтобы волна распространялась вблизи земной поверхности, она должна иметь вертикальную поляризацию, т.е. вектор электрического поля излучения должен быть вертикальным, и, следовательно, необходима вертикальная антенна. В действительности достаточно иметь антенну лишь половинной высоты; причиной тому является ее зеркальный заряд. Когда электромагнитное поле встречает на своем пути проводящую плоскость, оно зеркально отражается от нее. Поэтому электромагнитное поле, создаваемое над проводящей плоскостью некоторой системой токов и зарядов, оказывается идентичным полю, которое существовало бы, если бы вместо проводящей плоскости имелась зеркально отраженная система токов и зарядов, т.е. просто зеркальное отображение реальной системы в данной плоскости. Таким образом, поле над плоскостью - это поле вертикального полуволнового симметричного вибратора (рис. 1). Такой вибратор наиболее интенсивно излучает в плоскости, перпендикулярной его оси; в рассматриваемом случае это означает, что излучение направлено вдоль поверхности земли. Такая антенна на практике представляет собой стальную мачту высотой около четверти длины волны, установленную на опорных изоляторах (рис. 2). Землю делают хорошим проводником, закапывая в нее систему проводов, расходящихся в радиальных направлениях от основания антенны. Если антенную мачту для устойчивости снабжают проволочными оттяжками, то их надо разделить изоляторами на секции, достаточно короткие, чтобы влияние оттяжек на локальное поле антенны было незначительным.

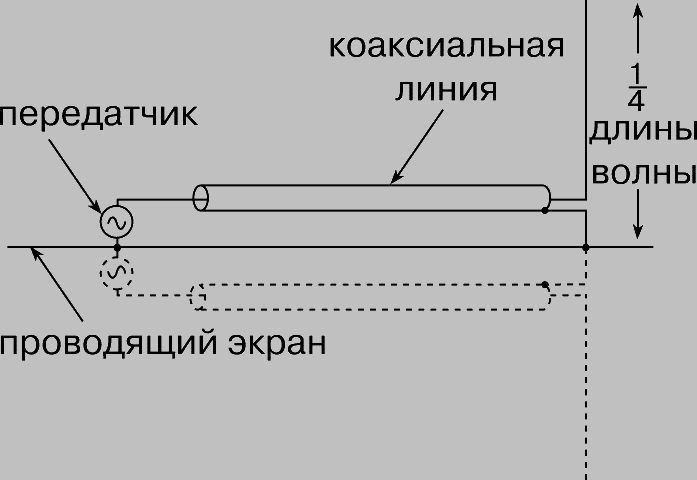
Рис. 1. ЧЕТВЕРТЬВОЛНОВАЯ АНТЕННА, установленная над проводящей плоскостью, действует как полуволновый симметричный вибратор, так как проводящий экран создает зеркальное "электрическое изображение" (показано штриховыми линиями), эквивалентное отсутствующей половине вибратора.

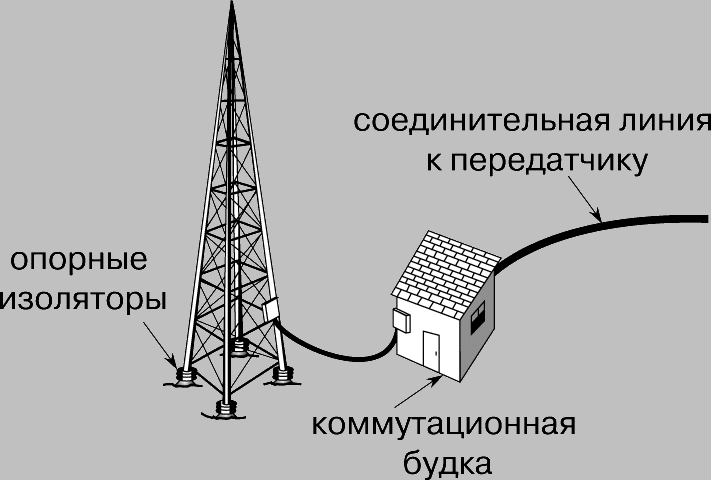
Рис. 2. СТАЛЬНАЯ МАЧТА на опорных изоляторах, действующая как четвертьволновая передающая антенна.

Направленные антенные решетки из антенных мачт. Существуют две причины, по которым широковещательной станции может требоваться направленная диаграмма излучения. Во-первых, ее "аудитория" может находиться преимущественно с одной стороны от места расположения передающей станции. Так, например, региональная станция, размещенная в приморском городе, должна создавать более сильный сигнал в континентальном направлении, если нежелательно, чтобы половина ее мощности терялась на морских просторах. Во-вторых, может возникнуть необходимость исключения взаимных помех в зоне, обслуживаемой какой-либо удаленной станцией, работающей на той же самой частоте; в этом случае диаграмма направленности данной станции должна иметь нулевое излучение в направлении на удаленную. Направленность излучения часто достигается созданием решетки из двух или большего числа антенных мачт, в которой расстояния между мачтами и фазы возбуждения антенн каждой из мачт выбраны так, чтобы получить желаемую диаграмму направленности. Проиллюстрируем данный подход примером. Пусть имеются две одинаковые антенные мачты, находящиеся друг от друга на расстоянии в половину длины волны и возбуждаемые токами одинаковой величины и фазы. Излучение каждой антенны равнонаправленно в горизонтальной плоскости; таким образом, если смотреть сверху, каждая из антенн выглядит как точечный источник круговых волн, распространяющихся равномерно во всех направлениях. Диаграмма направленности такой двухантенной решетки определяется наложением волн, излучаемых обеими антеннами. Как показано на рис. 3, точки, находящиеся на оси запад - восток (WE), от одной антенной мачты на полдлины волны дальше, чем от другой. Таким образом, в этих точках две излучаемые волны отличаются по фазе на 180° и, следовательно, гасят друг друга; в результате излучение по линии WE в обе стороны отсутствует. Точки же, расположенные на прямой север - юг (NS), напротив, находятся на одинаковом удалении от антенных мачт, так что обе волны в этих точках оказываются в одинаковой фазе и суммируются. Такая система называется антенной решеткой бокового (поперечного) излучения - ее диаграмма направленности представлена на рис. 4,а. Если же антенные мачты излучают в противофазе (разность фаз 180°), то вдоль оси NS будет происходить взаимное гашение волн, а вдоль оси WE - их сложение. Такая система называется антенной решеткой продольного (осевого) излучения. Ее диаграмма направленности похожа на диаграмму направленности решетки поперечного излучения, но повернута на 90° (рис. 4,б). Если две антенные мачты находятся друг от друга на расстоянии в четверть длины волны и возбуждаются токами равной величины, но волна, излучаемая восточной мачтой, опережает по фазе западную на 90°, то диаграмма направленности будет иметь форму кардиоиды (рис. 5, пунктирная линия). Штриховой и сплошной линиями на рисунке представлены диаграммы направленности, получаемые при опережении по фазе восточной мачтой на 45° и 180° соответственно.

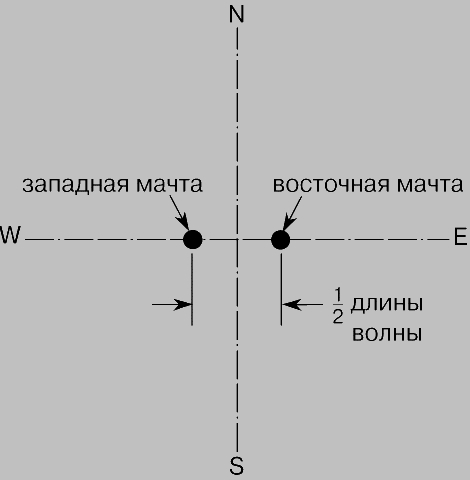
Рис. 3. ДВЕ АНТЕННЫЕ МАЧТЫ, разнесенные на полдлины волны, для получения диаграмм направленности, показанных на рис. 4, нужно возбуждать по-разному.

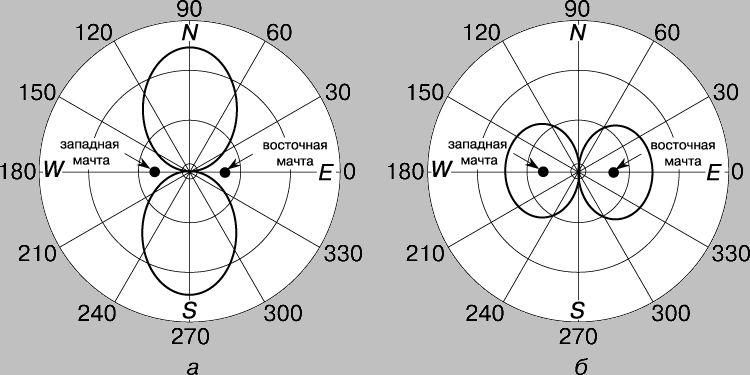
Рис. 4. ДИАГРАММЫ НАПРАВЛЕННОСТИ для антенн, показанных на рис. 3: а - поперечного излучения; б - продольного излучения.

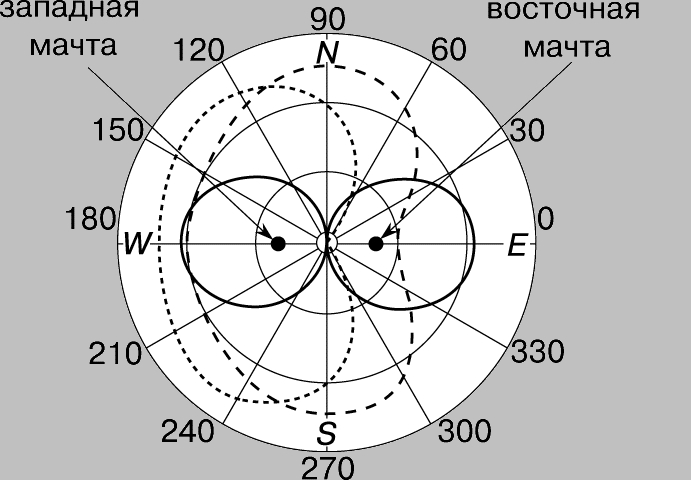
Рис. 5. ДИАГРАММЫ НАПРАВЛЕННОСТИ антенн, разнесенных на 1/4 длины волны.

Радиовещательные приемные антенны. Радиовещательные приемные антенны с высотой, близкой к половине или даже четверти длины волны, оказываются, как правило, непомерно большими. К счастью, это ограничение часто не играет существенной роли, так как напряженность поля, создаваемого передающей станцией, обычно настолько большая, что даже маленькая антенна обеспечивает более чем достаточный сигнал для современного радиоприемника. Исключая из рассмотрения крайне удаленные пункты, надо сказать, что длинная наружная антенна не улучшает отношение сигнал/шум и часто может лишь ухудшить прием. Большинство вещательных радиоприемников выпускаются со встроенной рамочной или ферритовой антенной. Такое устройство представляет собой электрически небольшой магнитный диполь. Если электрические и магнитные силовые линии, образующие поле антенны, поменять местами, то полученное в результате поле теоретически возможно в том смысле, что оно подчиняется законам электромагнетизма. Трудность состоит в том, что для излучения такого поля требуется магнитный аналог исходной излучающей системы; но магнитный аналог электрических зарядов, движущихся по электрическим проводникам, - это некие магнитные заряды, движущиеся по магнитным проводникам; однако ни магнитного заряда, ни магнитного проводника пока еще не удалось обнаружить. Существует, однако, магнитный аналог очень маленького диполя - катушка индуктивности. Хотя миниатюрный магнитный диполь, или рамочная антенна, как его называют, является весьма малоэффективной передающей антенной, такие качества, как миниатюрность и отличные возможности противостоять местным помехам и шумам, делают его идеальным средством для приема радиовещательных передач. Диаграмма направленности небольшой рамочной антенны представлена на рис. 6. Поворачивая рамку, можно, используя резко выраженные нули диаграммы, совпадающие с осью рамки, исключить прием помехи. Такая рамочная антенна может иметь форму плоской спирально намотанной катушки, размещаемой на задней стенке корпуса приемника, или форму тонкого соленоида с ферритовым сердечником. Благодаря резко выраженным нулям диаграммы направленности такую рамочную антенну используют в радиопеленгационной аппаратуре.

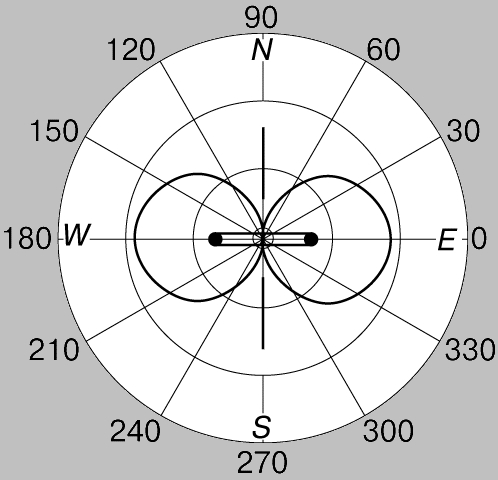
Рис. 6. ДИАГРАММА НАПРАВЛЕННОСТИ небольшой рамочной приемной антенны.

Диапазон ЧМ-радиовещания (от 88 до 108 МГц) заключен между нижним и верхним каналами ОВЧ-диапазона телевидения (от 2-го до 13-го канала); поэтому антенны, применяемые для передачи и приема ЧМ-сигналов, по существу такие же, как и используемые для телевидения, и хотя в последующем описании речь будет идти преимущественно о телевизионных антеннах, последние в большей или меньшей степени пригодны также и для ЧМ-радиовещания. Обычно и ЧМ-радиостанции, и телевизионные передающие станции ведут передачи на волнах с горизонтальной поляризацией.

АНТЕННЫ ДЛЯ ТЕЛЕВИЗИОННОГО И ЧМ-РАДИОВЕЩАНИЯ (54-216 мГц, 5,6 м - 72 см)

Телевизионные передающие антенны. От телевизионной (или ЧМ) передающей антенны обычно требуется, чтобы она давала равномерно распределенное (ненаправленное) излучение в горизонтальной плоскости; однако в вертикальной плоскости выгодно концентрировать излучение в сравнительно узкий луч, направленный к горизонту, ибо именно там находится обслуживаемая "аудитория" зрителей и слушателей. Энергия, направляемая выше или ниже линии горизонта, либо теряется в космосе, либо уходит в землю. Характеристики диаграммы направленности в вертикальной плоскости той или иной телевизионной передающей антенны можно определить сравнением с соответствующей диаграммой горизонтального полуволнового симметричного вибратора в вертикальной плоскости, содержащей этот вибратор. Коэффициент усиления антенны по мощности определяется как отношение входной мощности, подаваемой на выбранный для сравнения симметричный вибратор, к мощности, подаваемой на вход антенны, коэффициент усиления которой надо определить, при условии, что обе антенны дают одинаковую интенсивность излучения в горизонтальной плоскости на расстоянии в одну милю (1,6 км). Эффективная излучаемая мощность определяется как мощность в ваттах, поступающая по соединительной линии (фидеру) от передатчика в антенну, умноженная на коэффициент усиления антенны. Таким образом, эффективная излучаемая мощность в типичном случае получается намного больше фактической мощности передатчика. Одной из проблем конструирования антенны, решение которой особенно важно для телевещания, является исключение отражений от антенны обратно в соединительную линию. Эта отраженная энергия переотражается передатчиком в антенну, куда она попадает с задержкой, равной частному от деления двойной длины фидера на скорость света, и приводит к передаче в антенну задержанного эхо-сигнала. В худшем случае это эхо может проявить себя на принимаемой картинке как вторичное изображение (тускло воспроизводимое изображение, смещенное вправо), но даже при менее неприятных последствиях четкость получаемого изображения ухудшается. Проблема отражений, как и другие проблемы, связанные с конструкцией антенны, при передаче телевизионного сигнала усугубляются требованиями, предъявляемыми к ширине полосы тракта. Видеоинформация телевизионного сигнала занимает полосу около пяти мегагерц, что составляет почти 10% несущей частоты нижних каналов ТВ-диапазона. Это означает, что телевизионная передающая антенна должна иметь конструкцию, соответствующую жестким требованиям не только на одной частоте, но и в широкой полосе частот. Полуволновый проволочный симметричный вибратор был бы совершенно непригодным для передач телевидения, так как если даже согласовать его с фидером и добиться отсутствия отражений на какой-либо одной частоте, то при изменении частоты на 5% диполь будет отражать в фидер четверть подаваемой на его вход энергии. Применяемая на практике телевизионная передающая антенна представляет собой "турникетную" модель, которая состоит из двух скрещенных горизонтальных симметричных вибраторов, сделанных из труб диаметром 5 или 8 см. Каждый вибратор имеет в горизонтальной плоскости диаграмму направленности в форме цифры 8, и при возбуждении двух вибраторов со сдвигом по фазе на 90° суммарная диаграмма в той же плоскости становится почти всенаправленной. Направленность в вертикальной плоскости (а следовательно, и коэффициент усиления антенны) можно улучшить путем установки на антенной мачте нескольких ярусов турникетных антенн одну над другой. Турникетная антенна - это прототип одной из самых широко применяемых телевизионных передающих антенн, получившей название "супертурникетной". Вибраторы простой турникетной антенны приобрели в ней форму излучателей с конфигурацией бабочки - такая конфигурация позволяет получить намного большую ширину полосы вещания. Коэффициент усиления по мощности трехъярусной супертурникетной антенны составляет около 4.

Телевизионные приемные антенны. В отличие от волн, используемых для АМ-вещания, волны, на которых ведется телевещание, имеют значительно меньшую длину, так что приемные антенны размером в половину длины волны здесь вполне осуществимы. Так, телевизионный полуволновый симметричный вибратор настолько мал, что его можно сделать из жесткой трубки. Вместе с тем малый размер даже электрически длинной антенны на этих частотах означает, что эффективная площадь приема падающей волны (и, следовательно, возможность антенны захватить ее энергию) ограниченна. Кроме того, из-за большой ширины полосы телевизионного сигнала и шума, равномерно распределенного по каналу, приемник должен получить значительное количество энергии, чтобы обеспечить приемлемое отношение сигнал/шум. В свете вышесказанного становится понятным, что эффективность антенны играет важную роль в приеме телевизионного сигнала. На рабочих частотах телевещания атмосферные помехи не имеют особого значения, но приемная антенна будет улавливать массу индустриальных помех и космический шум. Поэтому важно, чтобы приемная антенна имела четко выраженную направленность, позволяющую не принимать сигналы, приходящие с направлений, не совпадающих с направлением на нужную передающую станцию. Другой тип помех, часто ухудшающих качество телевизионнного приема, - это многолучевое распространение, при котором нужный сигнал приходит на приемную антенну по двум путям разной длины. Так, например, один сигнал может прийти непосредственно от передатчика, а другой - отразившись от какой-либо горы или здания. Многолучевое распространение проявляется на экране в виде многоконтурности изображений, и, чтобы избавиться от него, надо использовать направленную антенну, позволяющую исключить прием по одному из двух лучей. Ширина полосы телевизионной приемной антенны должна быть очень большой, поскольку от нее требуется охватить не один канал, а обычно все тринадцать, размещенные в диапазоне частот 4:1. К счастью, согласование линии передачи с антенной, при котором отражения не возникают, не так существенно на приемной стороне, где рассогласование приводит лишь к потере слабого сигнала, не порождая эхо-сигналов. Важное значение имеет, однако, согласование соединительной линии с приемником, но в этом случае следует уделить внимание конструкции приемника. Отражения, возникающие на неоднородностях соединительной линии, могут вызывать многоконтурность или потерю резкости изображения. Такие отражения часто возникают, если двухпроводной ленточный кабель проходит слишком близко к металлическим конструкциям, например таким, как лотки для проводов или водостоки. Это станет понятным, если вспомнить, что высокочастотная электромагнитная энергия распространяется в поле, возникающем вокруг проводов, которые служат проводниками этого поля. Одна из самых простых антенн, используемых для приема телевизионного сигнала, представляет собой полуволновый петлевой симметричный вибратор (рис. 7), отличающийся от обычного полуволнового симметричного вибратора тем, что его выходной импеданс (300 Ом) согласуется с широко применяемыми типами фидеров, а также тем, что он обладает более широкой полосой; иначе говоря, он эффективно передает принимаемую электромагнитную энергию более широкого диапазона частот в соединительную линию.

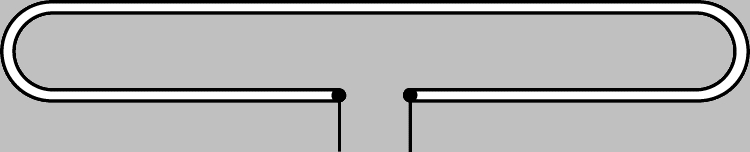
Рис. 7. ПОЛУВОЛНОВЫЙ ПЕТЛЕВОЙ СИММЕТРИЧНЫЙ ВИБРАТОР, используемый для приема телевидения и ЧМ-радиовещания.

Чтобы получить нужную диаграмму направленности в горизонтальной и вертикальной плоскостях, базовую антенну обычно используют совместно с одним или несколькими пассивными элементами. Пассивный элемент - это еще одна антенна, размещенная вблизи от основной, но не подсоединенная к фидеру. С основной антенной (а следовательно, и с приемником) она связана только локальными полями. Понять, как пассивный элемент влияет на диаграмму направленности антенны, легко, поскольку здесь, по существу, используется тот же принцип, что и в ненаправленной антенной решетке; разница же состоит в том, что в данном случае возбуждается только одна антенна, а другая принимает энергию лишь от ее ближнего поля. Для примера отметим, что стержень полуволновой длины, помещенный (как показано на рис. 8) на расстоянии в четверть длины волны от полуволнового симметричного вибратора, действует как отражатель. Почему это действительно так, можно пояснить следующим образом. Локальное поле возбуждаемой (основной) антенны индуцирует в пассивном элементе заряды и токи противоположного знака, но из-за расстояния в четверть длины волны эти токи и заряды отстают от соответствующих токов и зарядов в основной антенне приблизительно на четверть периода, т.е. ток в пассивном элементе опережает ток в основной антенне приблизительно на 90°. Диаграмма направленности возбуждаемой антенны с пассивным элементом определяется путем наложения обоих излучаемых волновых полей. Эта ситуация очень похожа на рассмотренную для ненаправленной (в горизонтальной плоскости) решетки АМ-вещания; ее диаграмма направленности показана пунктирной линией на рис. 5. Эти две волны имеют тенденцию гасить друг друга в направлении к пассивному элементу и усиливать друг друга в противоположном направлении; следовательно, пассивный элемент действует как отражатель. Пассивный элемент не обязательно должен находиться на расстоянии в четверть волны от возбуждаемой антенны. Если его поместить очень близко к ней, например на расстоянии всего 0,1 длины волны, он тем не менее будет действовать как отражатель, если его длину сделать чуть больше половины длины волны. Увеличение длины пассивного элемента делает его индуктивным, в результате чего текущий по нему ток отстает по фазе от электродвижущей силы, индуцируемой полем основной антенны. Если же близко расположенный пассивный элемент сделать чуть короче половины длины волны, он становится направляющим ("директором") и концентрирует излучение на своей стороне от основной антенны. Все вышесказанное имеет непосредственное отношение и к приемным антеннам. Поскольку диаграммы направленности при передаче и приеме одинаковы, пассивные директоры и отражатели можно использовать в телевизионных приемных антеннах для получения необходимой диаграммы направленности. Типичная высоконаправленная антенная решетка с одним отражателем и тремя директорами показана на рис. 9.

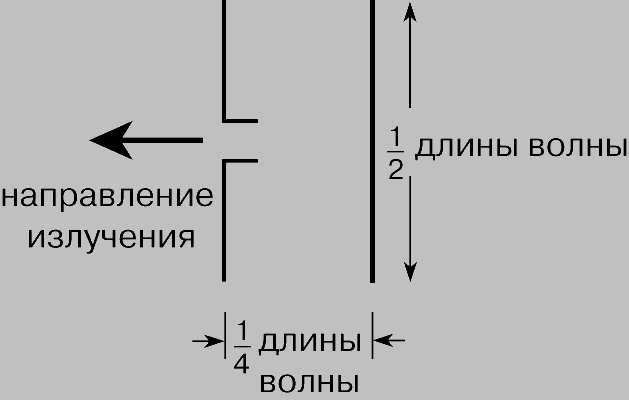
Рис. 8. ОТРАЖАЮЩИЙ ЭЛЕМЕНТ - стержень полуволновой длины (справа) расположен на 1/4 длины волны позади полуволнового симметричного вибратора (слева).

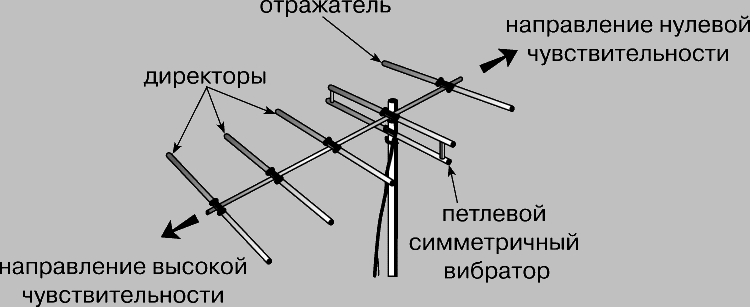
Рис. 9. ОСТРОНАПРАВЛЕННАЯ ПРИЕМНАЯ АНТЕННА с одним отражателем (сзади) и тремя директорами (спереди) петлевого симметричного вибратора.

ЛИТЕРАТУРА

Кочержевский Г.Н. Антенно-фидерные устройства. М., 1981 Кинбер Б.Е., Классен В.И. Теория и техника антенн. М., 1985 Сазонов Д.М. Антенны и устройства СВЧ. М., 1988 Драбкин А.Л. и др. Антенны. М., 1995

Составить слова из слова антенна

АРИФМЕТИКА - искусство вычислений, производимых с положительными действительными числами.

Краткая история арифметики. С глубокой древности работа с числами подразделялась на две различные области: одна касалась непосредственно свойств чисел, другая была связана с техникой счета. Под "арифметикой" во многих странах обычно имеется ввиду именно эта последняя область, которая несомненно является старейшей отраслью математики. По-видимому, наибольшую трудность у древних вычислителей вызывала работа с дробями. Об этом можно судить по папирусу Ахмеса (называемому также папирусом Ринда), древнеегипетскому сочинению по математике, датируемому примерно 1650 до н.э. Все дроби, упоминаемые в папирусе, за исключением 2/3, имеют числители, равные 1. Трудность обращения с дробями заметна и при изучении древневавилонских клинописных табличек. И древние египтяне, и вавилоняне, по-видимому, производили вычисления с помощью некоторой разновидности абака. Наука о числах получила у древних греков существенное развитие начиная с Пифагора, около 530 до н.э. Что же касается непосредственно техники вычисления, то в этой области греками было сделано гораздо меньше. Жившие позднее римляне, напротив, практически не внесли никакого вклада в науку о числе, зато исходя из нужд быстро развивавшихся производства и торговли усовершенствовали абак как счетное устройство. О зарождении индийской арифметики известно очень мало. До нас дошли лишь некоторые более поздние работы о теории и практике операций с числами, написанные уже после того, как индийская позиционная система была усовершенствована посредством включения в нее нуля. Когда в точности это произошло, нам достоверно неизвестно, но именно тогда были заложены основы для наших наиболее распространенных арифметических алгоритмов

(см. также ЦИФРЫ И СИСТЕМЫ СЧИСЛЕНИЯ).

Индийская система счисления и первые арифметические алгоритмы были заимствованы арабами. Самый ранний из дошедших до нас арабских учебников арифметики был написан аль-Хорезми около 825. В нем широко используются и объясняются индийские цифры. Позднее этот учебник был переведен на латынь и оказал значительное влияние на Западную Европу. Искаженный вариант имени аль-Хорезми дошел до нас в слове "алгоризм", которое при дальнейшем смешении с греческим словом аритмос превратилось в термин "алгоритм". Индо-арабская арифметика стала известна в Западной Европе в основном благодаря сочинению Л.Фибоначчи Книга абака (Liber abaci, 1202). Метод абацистов предлагал упрощения, подобные использованию нашей позиционной системы, во всяком случае для сложения и умножения. Абацистов сменили алгоритмики, которые использовали нуль и арабский метод деления и извлечения квадратного корня. Один из первых учебников арифметики, автор которого нам неизвестен, вышел в Тревизо (Италия) в 1478. В нем речь шла о расчетах при совершении торговых сделок. Этот учебник стал предшественником многих появившихся впоследствии учебников арифметики. До начала 17 в. в Европе было опубликовано более трехсот таких учебников. Арифметические алгоритмы за это время были существенно усовершенствованы. В 16-17 вв. появились символы арифметических операций, такие как =, +, -, *, "корень" и /. Принято считать, что десятичные дроби изобрел в 1585 С.Стевин, логарифмы - Дж. Непер в 1614, логарифмическую линейку - У. Оутред в 1622. Современные аналоговые и цифровые вычислительные устройства были изобретены в середине 20 в.

См. также

МАТЕМАТИКА;

МАТЕМАТИКИ ИСТОРИЯ;

ЧИСЕЛ ТЕОРИЯ;

РЯДЫ.

Механизация арифметических вычислений. С развитием общества росла и потребность в более быстрых и точных вычислениях. Эта потребность вызвала к жизни четыре замечательных изобретения: индо-арабские числовые обозначения, десятичные дроби, логарифмы и современные вычислительные машины. На самом деле простейшие счетные устройства существовали до появления современной арифметики, ибо в древности элементарные арифметические операции производились на абаке (в России с этой целью использовались счеты). Простейшим современным вычислительным устройством можно считать логарифмическую линейку, представляющую собой две скользящие одна вдоль другой логарифмические шкалы, что позволяет производить умножение и деление, суммируя и вычитая отрезки шкал. Изобретателем первой механической суммирующей машины принято считать Б.Паскаля (1642). Позднее в том же столетии Г. Лейбниц (1671) в Германии и С. Морленд (1673) в Англии изобрели машины для выполнения умножения. Эти машины стали предшественницами настольных вычислительных устройств (арифмометров) 20 в., позволявших быстро и точно производить операции сложения, вычитания, умножения и деления. В 1812 английский математик Ч. Бэббидж приступил к созданию проекта машины для вычисления математических таблиц. Хотя работа над проектом продолжалась долгие годы, она так и осталась незавершенной. Тем не менее проект Бэббиджа послужил стимулом к созданию современных электронных вычислительных машин, первые образцы которых появились около 1944. Быстродействие этих машин поражало воображение: с их помощью за минуты или часы удавалось решить задачи, ранее требовавшие многих лет непрерывных вычислений даже с применением арифмометров. Суть дела можно пояснить на примере конкретной арифметической задачи, например, вычисления числа p (отношения длины окружности к ее диаметру). Первые систематические попытки вычисления p встречаются у Архимеда (ок. 240 до н.э.). Используя весьма несовершенную систему счисления, он после долгих трудов сумел вычислить p с точностью, эквивалентной в нашей современной системе счисления двум знакам после запятой. Используя метод Архимеда, Л.ван Цейлен (1540-1610), посвятив этому значительную часть жизни, сумел вычислить p с точностью 35 знаков после запятой. В 1873 после пятнадцати лет работы У.Шенкс получил значение p с 707 знаками, но позднее выяснилось, что начиная с 528-го знака в его вычисления вкрались ошибки. В 1958 компьютер фирмы ИБМ вычислил за 40 секунд 707 знаков числа p и, продолжая далее вычисления, получил за 100 минут 10000 знаков.

См. также КОМПЬЮТЕР; ЧИСЛО ПИ. Целые положительные числа. Основой наших представлений о числах являются интуитивные понятия множества, соответствия между множествами и бесконечной последовательности различимых знаков или звуков. Знакомая всем нам последовательность символов 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ... есть не что иное, как бесконечная последовательность различимых знаков и бесконечная последовательность различимых звуков (или слов) "один", "два", "три", "четыре", "пять", "шесть", "семь", "восемь", "девять", "десять", "одиннадцать", "двенадцать", ..., соответствующих определенным символам. Любое множество, все элементы которого можно поставить во взаимно однозначное соответствие с элементами некоторого начального сегмента нашей бесконечной последовательности символов, называется конечным множеством. При этом на число элементов множества указывает последний символ сегмента. Например, множество предметов, которые можно поставить во взаимно однозначное соответствие с начальным сегментом 1, 2, 3, 4, 5, 6, 7, 8, является конечным множеством, содержащим 8 ("восемь") элементов. Символ 8 указывает на "число" предметов в исходном множестве. Это число есть символ, или ярлык, приписываемый данному множеству. Этот же ярлык приписывается всем тем и только тем множествам, которые могут быть поставлены во взаимно однозначное соответствие с данным множеством. Однозначное определение ярлыка для любого заданного конечного множества называется "пересчитыванием" элементов данного множества, а сами ярлыки получили название натуральных или целых положительных чисел

(см. также ЧИСЛО; МНОЖЕСТВ ТЕОРИЯ). Пусть A и B - два конечных множества, не имеющие общих элементов, и пусть A содержит n элементов, а B содержит m элементов. Тогда множество S, состоящее из всех элементов множеств A и B, взятых вместе, является конечным множеством, содержащим, скажем, s элементов. Например, если А состоит из элементов {a, b, c}, множество В - из элементов {x, y}, то множество S = A + B и состоит из элементов {a, b, c, x, y}. Число s называется суммой чисел n и m, и мы записываем это так: s = n + m. В этой записи числа n и m называются слагаемыми, операция нахождения суммы - сложением. Символ операции "+" читается как "плюс". Множество P, состоящее из всех упорядоченных пар, в которых первый элемент выбран из множества A, а второй - из множества B, является конечным множеством, содержащим, скажем, p элементов. Например, если, как и прежде, A = {a, b, c}, B = {x, y}, то P = AґB = {(a,x), (a,y), (b,x), (b,y), (c,x), (c,y)}. Число p называется произведением чисел a и b, и мы записываем это так: p = a*b или p = a*b. Числа a и b в произведении называются множителями, операция нахождения произведения - умножением. Символ операции ґ читается как "умноженное на". Можно показать, что из этих определений следуют приводимые ниже фундаментальные законы сложения и умножения целых чисел: - закон коммутативности сложения: a + b = b + a; - закон ассоциативности сложения: a + (b + c) = (a + b) + c; - закон коммутативности умножения: a*b = b*a; - закон ассоциативности умножения: a*(b*c) = (a*b)*c; - закон дистрибутивности: aґ(b + c)= (a*b) + (a*c). Если a и b - два положительных целых числа и если существует положительное целое число c, такое, что a = b + c, то мы говорим, что a больше b (это записывается так: a > b), или что b меньше a (это записывается так: b < a). Для любых двух чисел a и b выполняется одно из трех соотношений: либо a = b, либо a > b, либо a < b. Первые два фундаментальных закона говорят о том, что сумма двух или большего числа слагаемых не зависит от того, как они сгруппированы и в каком порядке они расположены. Аналогично, из третьего и четвертого законов следует, что произведение двух или большего числа множителей не зависит от того, как сгруппированы множители и каков их порядок. Эти факты известны как "обобщенные законы коммутативности и ассоциативности" сложения и умножения. Из них следует, что при написании суммы нескольких слагаемых или произведения нескольких множителей порядок слагаемых и множителей несуществен и можно опустить скобки. В частности, повторная сумма a + a + ... + a из n слагаемых равна n*a. Повторное произведение a*a* ... *a из n множителей условились обозначать an; число a называется основанием, а число n - показателем повторного произведения, само повторное произведение - n-й степенью числа a. Эти определения позволяют установить следующие фундаментальные законы для показателей степени:

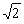
Еще одно важное следствие из определений: a*1 = a для любого целого числа a, причем 1 - единственное целое число, обладающее этим свойством. Число 1 называется единицей.

Делители целых чисел. Если a, b, c - целые числа и aґb = c, то a и b являются делителями числа c. Так как aґ1 = a для любого целого числа a, мы заключаем, что 1 - делитель любого целого числа и что любое целое число есть делитель самого себя. Любой делитель целого числа a, отличный от 1 или a, получил название собственного делителя числа a. Любое целое число, отличное от 1 и не имеющее собственных делителей, называется простым числом. (Примером простого числа может служить число 7.) Целое число, имеющее собственные делители, называется составным числом. (Например, число 6 составное, так как 2 делит 6.) Из сказанного следует, что множество всех целых чисел подразделяется на три класса: единица, простые числа и составные числа. В теории чисел есть очень важная теорема, которая утверждает, что "любое целое число может быть представлено в виде произведения простых чисел, и с точностью до порядка множителей такое представление единственно". Эта теорема известна как "основная теорема арифметики". Она показывает, что простые числа служат теми "кирпичиками", из которых с помощью умножения можно построить все целые числа, отличные от единицы. Если задано некоторое множество целых чисел, то наибольшее целое число, которое является делителем каждого числа, входящего в это множество, называется наибольшим общим делителем данного множества чисел; наименьшее целое число, делителем которого служит каждое число из данного множества, называется наименьшим общим кратным данного множества чисел. Так, наибольший общий делитель чисел 12, 18 и 30 равен 6. Наименьшее общее кратное тех же самых чисел равно 180. Если наибольший общий делитель двух целых чисел a и b равен 1, то числа a и b называются взаимно простыми. Например, числа 8 и 9 - взаимно простые, хотя ни одно из них не является простым. Положительные рациональные числа. Как мы видели, целые числа являются абстракциями, возникающими из процесса пересчета конечных наборов предметов. Однако для потребностей повседневной жизни целых чисел оказывается недостаточно. Например, при измерении длины крышки стола принятая единица измерения может оказаться слишком большой и не укладываться целое число раз в измеряемой длине. Чтобы справиться с подобной трудностью, с помощью т.н. дробных (т.е., буквально, "поломанных") чисел вводится меньшая единица длины. Если d - некоторое целое число, то дробная единица 1/d определяется свойством dґ1/d = 1, и если n - целое число, то nґ1/d мы записываем просто как n/d. Такие новые числа получили название "обыкновенных" или "простых" дробей. Целое число n называется числителем дроби, а число d - знаменателем. Знаменатель показывает, на сколько равных долей разделили единицу, а числитель показывает, сколько таких долей взяли. Если n < d, дробь называется правильной; если же n = d или n > d, то - неправильной. Целые числа рассматриваются как дроби с знаменателем, равным 1; например, 2 = 2/1. Так как дробь n/d можно интерпретировать как результат деления n единиц на d равных долей и взятия одной из таких долей, дробь можно рассматривать как "частное" или "отношение" двух целых чисел n и d, а черту дроби понимать как знак деления. Поэтому дроби (в т.ч. и целые числа как частный случай дробей) обычно называют рациональными числами (от лат. ratio - отношение). Две дроби n/d и (k*n)/(k*d), где k - целое число, можно рассматривать как равные; например, 4/6 = 2/3. (Здесь n = 2, d = 3 и k = 2.) Это обстоятельство известно как "основное свойство дроби": значение любой дроби не изменится, если числитель и знаменатель дроби умножить (или разделить) на одно и то же число. Отсюда следует, что любую дробь можно записать как отношение двух взаимно простых чисел. Из предложенной выше интерпретации дроби также следует, что в качестве суммы двух дробей n/d и m/d, имеющих один и тот же знаменатель, следует принять дробь (n + m)/d. При сложении дробей с разными знаменателями нужно сначала преобразовать их, пользуясь основным свойством дроби, в эквивалентные дроби с одинаковым (общим) знаменателем. Например, n1/d1 = (n1*d2)/(d1*d2) и n2/d2 = (n2*d1)/(d1*d2), откуда

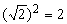
Можно было бы поступить иначе и сначала найти наименьшее общее кратное, скажем, m, знаменателей d1 и d2. Тогда существуют целые числа k1 и k2, такие, что m = k1*d1 = k2*d2, и мы получаем:

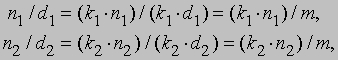
откуда

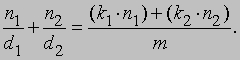
При таком способе число m обычно называется наименьшим общим знаменателем двух дробей. Эти два результата эквивалентны по определению равенства дробей. Произведение двух дробей n1/d1 и n2/d2 принимается равным дроби (n1*n2)/(d1*d2).

Восемь фундаментальных законов, приведенных выше для целых чисел, справедливы и в том случае, если под a, b, c понимать произвольные положительные рациональные числа. Кроме того, если даны два положительных рациональных числа n1/d1 и n2/d2, то мы говорим, что n1/d1 > n2/d2 тогда и только тогда, когда n1*d2 > n2*d1. Положительные действительные числа. Применение чисел для измерения длин отрезков прямых наводит на мысль, что для любых двух данных отрезков прямых AB и CD должен существовать некоторый отрезок UV, возможно, очень малый, который можно было бы отложить целое число раз в каждом из отрезков AB и CD. Если такая общая единица измерения длины UV существует, то отрезки AB и CD называются соизмеримыми. Уже в древности пифагорейцы знали о существовании несоизмеримых отрезков прямых. Классический пример - сторона квадрата и его диагональ. Если принять сторону квадрата за единицу длины, то не найдется такого рационального числа, которое могло бы быть мерой диагонали этого квадрата. Убедиться в этом можно, рассуждая от противного. Действительно, предположим, что рациональное число n/d есть мера диагонали. Но тогда отрезок 1/d можно было бы отложить n раз на диагонали и d раз на стороне квадрата вопреки тому, что диагональ и сторона квадрата несоизмеримы. Следовательно, независимо от выбора единицы длины не все отрезки прямых имеют длины, выражаемые рациональными числами. Чтобы все отрезки прямой можно было измерять с помощью некоторой единицы длины, система счисления должна быть расширена таким образом, чтобы она включала числа, представляющие результаты измерения длин отрезков прямых, несоизмеримых с выбранной единицей длины. Эти новые числа называются положительными иррациональными числами. Последние вместе с положительными рациональными числами образуют более широкое множество чисел, элементы которого называются положительными действительными числами. Если OR - горизонтальная полупрямая, исходящая из точки O, U - точка на OR, отличная от начала координат O, и OU выбран в качестве единичного отрезка, то каждой точке P на полупрямой OR можно поставить в соответствие единственное положительное действительное число p, выражающее длину отрезка OP. Таким образом мы устанавливаем взаимно однозначное соответствие между положительными действительными числами и точками, отличными от O, на полупрямой OR. Если p и q - два положительных действительных числа, соответствующих точкам P и Q на OR, то мы пишем p > q, p = q или p < q в зависимости от того, расположена точка P справа от точки Q на OR, совпадает с Q или расположена слева от Q.

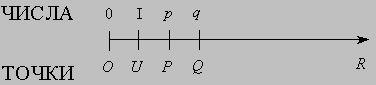
Введение положительных иррациональных чисел существенно расширило сферу применимости арифметики. Например, если a - любое положительное действительное число и n - любое целое число, то существует единственное положительное действительное число b, такое, что bn = a. Это число b называется корнем n-й степени из a и записывается как , где символ по своим очертаниям напоминает латинскую букву r, с которой начинается латинское слово radix (корень) и называется радикалом . Можно показать, что

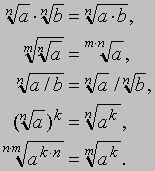
Эти соотношения известны как основные свойства радикалов. С практической точки зрения очень важно, что любое положительное иррациональное число можно сколь угодно точно аппроксимировать положительным рациональным числом. Это означает, что если r - положительное иррациональное число и e - сколь угодно малое положительное рациональное число, то можно найти положительные рациональные числа a и b, такие, что a < r < b и b < a + e. Например, число иррационально. Если выбрать e = 0,01, то ; если же выбрать e = 0,001, то . Индо-арабская система счисления. Алгоритмы, или схемы вычислений, арифметики зависят от используемой системы счисления. Совершенно очевидно, например, что методы вычислений, придуманные для римской системы счисления, могут отличаться от алгоритмов, изобретенных для действующей ныне индо-арабской системы. Более того, некоторые системы счисления могут оказаться совсем неподходящими для построения арифметических алгоритмов. Исторические данные свидетельствуют, что до принятия индо-арабской системы обозначения чисел вообще не существовало каких-либо алгоритмов, позволявших достаточно легко с помощью "карандаша и бумаги" выполнять сложение, вычитание, умножение и деление чисел. За долгие годы существования индо-арабской системы были разработаны специально к ней приспособленные многочисленные алгоритмические процедуры, так что наши современные алгоритмы являются продуктом целой эпохи развития и усовершенствования (см. также ЦИФРЫ И СИСТЕМЫ СЧИСЛЕНИЯ) . В индо-арабской системе счисления каждая запись, обозначающая число, представляет собой набор из десяти основных символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называемых цифрами. Например, индо-арабское обозначение числа четыреста двадцать три имеет вид последовательности цифр 423. Значение цифры в индо-арабской записи числа определяется ее местом, или позицией, в последовательности цифр, образующих эту запись. В приведенном нами примере цифра 4 означает четыре сотни, цифра 2 - два десятка и цифра 3 - три единицы. Очень важную роль играет цифра 0 (нуль), используемая для заполнения пустых позиций; например, запись 403 означает число четыреста три, т.е. отсутствуют десятки. Если a, b, c, d, e означают отдельные цифры, то в индо-арабской системе abcde означает сокращенную запись целого числа

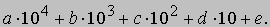
Так как каждое целое число допускает единственное представление в виде

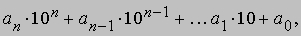
где n - целое число, а a0, a1, ..., an - цифры, мы заключаем, что в данной системе счисления каждое целое число можно представить единственным способом. Индо-арабская система счисления позволяет сжато записывать не только целые, но и любые положительные действительные числа. Введем обозначение 10-n для 1/10n, где n - произвольное положительное целое число. Тогда, как можно показать, любое положительное действительное число представимо, причем единственным образом, в виде

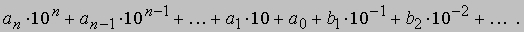
Эту запись можно сжать, записав в виде последовательности цифр

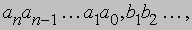
где знак, называемый десятичной запятой, между a0 и b1 указывает, где начинаются отрицательные степени числа 10 (в некоторых странах с этой целью используется точка). Такой способ записи положительного действительного числа получил название десятичного разложения, а дробь, представленная в виде своего десятичного разложения, - десятичной. Можно показать, что для положительного рационального числа десятичное разложение после запятой либо обрывается (например, 7/4 = 1,75), либо повторяется (например, 6577/1980 = 3,32171717...). Если число иррационально, то его десятичное разложение не обрывается и не повторяется. Если десятичное разложение иррационального числа на каком-то знаке после запятой оборвать, мы получим его рациональное приближение. Чем дальше справа от запятой расположен знак, на котором мы обрываем десятичное разложение, тем лучше рациональное приближение (тем меньше ошибка). В индо-арабской системе число записывается с помощью десяти основных цифр, значение которых зависит от их места, или позиции, в записи числа (значение цифры равно произведению цифры на некоторую степень числа 10). Поэтому такая система называется десятичной позиционной системой. Позиционные системы счисления очень удобны для построения арифметических алгоритмов, и именно этим объясняется столь широкое распространение индо-арабской системы счисления в современном мире, хотя в разных странах для обозначения отдельных цифр могут использоваться разные символы.

Названия чисел. Названия чисел в индо-арабской системе строятся по определенным правилам. Наиболее употребительный способ наименования чисел заключается в том, что число прежде всего делят на группы из трех цифр справа налево. Эти группы называются "периодами". Первый период называется периодом "единиц", второй - периодом "тысяч", третий - периодом "миллионов" и т.д., как показано на следующем примере:

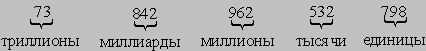
Каждый период читается так, как если бы он был трехзначным числом. Например, период 962 читается как "девятьсот шестьдесят два". Чтобы прочитать число, состоящее из нескольких периодов, прочитывается группа цифр в каждом периоде, начиная с самого левого и далее по порядку слева направо; после каждой группы следует название периода. Например, приведенное выше число читается как "семьдесят три триллиона восемьсот сорок два миллиарда девятьсот шестьдесят два миллиона пятьсот тридцать две тысячи семьсот девяносто восемь". Обратите внимание на то, что при чтении и записи целых чисел союз "и" обычно не используется. Название разряда единиц опускается. За триллионами следуют квадриллионы, квинтиллионы, секстиллионы, септиллионы, октиллионы, ноналлионы, дециллионы. Каждый период имеет значение, в 1000 раз превышающее значение предыдущего. В индо-арабской системе принято придерживаться следующей процедуры чтения цифр, стоящих справа от десятичной запятой. Здесь позиции называются (по порядку слева направо): "десятые", "сотые", "тысячные", "десятитысячные" и т.д. Правильная десятичная дробь читается так, как если бы цифры после десятичной запятой образовывали целое число, после чего добавляется название позиции последней справа цифры. Например, 0,752 читается как "семьсот пятьдесят две тысячных". Смешанное десятичное число читается путем объединения правила наименования целых чисел с правилом наименования правильных десятичных дробей. Например, 632,752 читается как "шестьсот тридцать две целых семьсот пятьдесят две тысячных". Обратите внимание на слово "целых", произносимое перед десятичной запятой. В последние годы десятичные числа все чаще читают более просто, например, 3,782 как "три запятая семьсот восемьдесят два".

Сложение. Теперь мы уже готовы к тому, чтобы проанализировать арифметические алгоритмы, с которыми знакомят в начальной школе. Эти алгоритмы относятся к действиям над положительными действительными числами, записанными в виде десятичных разложений. Мы предполагаем, что элементарные таблицы сложения и умножения выучены наизусть. Рассмотрим задачу на сложение: вычислить 279,8 + 5,632 + 27,54:

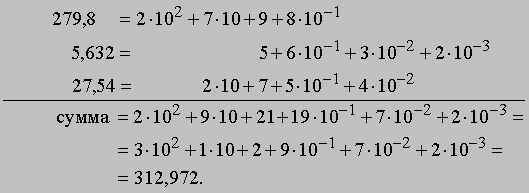
Сначала мы суммируем одинаковые степени числа 10. Число 19*10-1 разбивается по дистрибутивному закону на 9*10-1 и 10*10-1 = 1. Единицу мы переносим влево и прибавляем к 21, что дает 22. В свою очередь, число 22 мы разбиваем на 2 и 20 = 2*10. Число 2*10 переносим влево и прибавляем к 9*10, что дает 11*10. Наконец, 11*10 разбиваем на 1*10 и 10*10 = 1*102, 1*102 переносим влево и прибавляем к 2*102, что дает 3*102. Окончательная сумма оказывается равной 312,972. Ясно, что проделанные вычисления можно представить в более сжатой форме, заодно использовав ее как пример алгоритма сложения, которому учат в школе. Для этого все три числа мы выписываем одно под другим так, чтобы десятичные запятые оказались на одной вертикали:

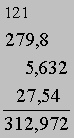
Начав справа, находим, что сумма коэффициентов при 10-3 равна 2, что и записываем в соответствующем столбце под чертой. Сумма коэффициентов при 10-2 равна 7, что также записываем в соответствующем столбце под чертой. Сумма коэффициентов при 10-1 равна 19. Число 9 мы записываем под чертой, а 1 переносим в предыдущий столбец, где стоят единицы. С учетом этой единицы сумма коэффициента в этом столбце оказывается равной 22. Мы записываем одну двойку под чертой, а другую переносим в предыдущий столбец, где стоят десятки. С учетом перенесенной двойки сумма коэффициентов в этом столбце равна 11. Одну единицу мы записываем под чертой, а другую переносим в предыдущий столбец, где стоят сотни. Сумма коэффициентов в этом столбце оказывается равной 3, что и записываем под чертой. Требуемая сумма равна 312,972.

Вычитание. Вычитание - это действие, обратное сложению. Если три положительных действительных числа a, b, c связаны между собой так, что a + b = c, то мы записываем a = c - b, где символ "-" читается как "минус". Нахождение числа a по известным числам b и c называется "вычитанием". Число c называется уменьшаемым, число b - "вычитаемым", а число a - "разностью". Поскольку мы имеем дело с положительными действительными числами, должно выполняться условие c > b. Рассмотрим пример на вычитание: вычислить 453,87 - 82,94.

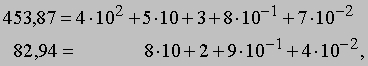
или

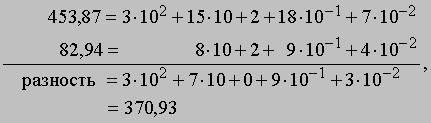
Прежде всего, заимствуя в случае необходимости единицу слева, мы преобразуем разложение уменьшаемого так, чтобы его коэффициент при любой степени числа 10 был больше коэффициента вычитаемого при той же степени. Из 4Ч102 мы заимствуем 1Ч102 = 10Ч10, прибавляя последнее число к следующему члену разложения, что дает 15Ч10; аналогично мы заимствуем 1Ч100, или 10Ч10-1, и прибавляем это число к предпоследнему члену разложения. После этого мы получаем возможность произвести вычитание коэффициентов при одинаковых степенях числа 10 и без труда находим разность 370,93. Запись операций вычитания можно представить в более сжатом виде и получить пример алгоритма вычитания, изучаемого в школе. Запишем вычитаемое под уменьшаемым так, чтобы их десятичные запятые оказались на одной вертикали. Начав справа, найдем, что разность коэффициентов при 10-2 равна 3, и это число запишем в том же столбце под чертой. Так как в следующем столбце слева мы не можем вычесть 9 из 8, мы изменяем тройку в положении единиц уменьшаемого на двойку и рассматриваем число 8 в позиции десятых как 18. После вычитания 9 из 18 мы получаем 9 и т.д., т.е.

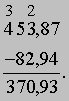
Умножение. Рассмотрим сначала т.н. "короткое" умножение - умножение положительного действительного числа на одно из однозначных чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, например, 32,67ґ4. Пользуясь законом дистрибутивности, а также законами ассоциативности и коммутативности умножения, мы получаем возможность разбивать множители на части и располагать их более удобным образом. Например,

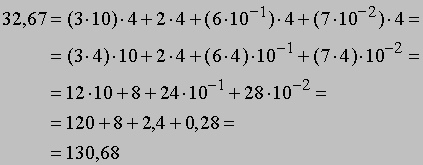
Эти вычисления можно записать более компактно следующим образом:

Процесс сжатия можно продолжить. Запишем множитель 4 под множимым 32,67, как указано:

Так как 4*7 = 28, мы записываем под чертой цифру 8, а 2 помещаем над цифрой 6 множимого. Далее, 4*6 = 24, что с учетом перенесенной из столбца справа дает 26. Цифру 6 мы записываем под чертой, а 2 записываем над цифрой 2 множимого. Затем мы получаем 4*2 = 8, что в сочетании с перенесенной двойкой дает 10. Цифру 0 мы подписываем под чертой, а единицу - над цифрой 3 множимого. Наконец, 4ґ3 = 12, что с учетом перенесенной единицы дает 13; число 13 записываем под чертой. Поставив десятичную запятую, получаем ответ: произведение равно 130,68. "Длинное" умножение - это просто неоднократно повторенное "короткое" умножение. Рассмотрим, например, умножение числа 32,67 на число 72,4. Расположим множитель под множимым, как указано:

Производя справа налево короткое умножение, мы получаем первое частное произведение 13,068, второе - 65,34 и третье - 2286,9. По закону дистрибутивности, произведение, которое требуется найти, есть сумма этих частных произведений, или 2365,308. В письменной записи десятичная запятая в частных произведениях опускается, но их нужно правильно располагать "ступеньками", чтобы затем просуммировать и получить полное произведение. Число знаков после десятичной запятой в произведении равно сумме числа знаков после запятых в множимом и множителе.

Деление. Деление - операция, обратная умножению; подобно тому, как умножение заменяет неоднократно повторенное сложение, деление заменяет неоднократно повторенное вычитание. Рассмотрим, например, такой вопрос: сколько раз 3 содержится в 14? Повторяя операцию вычитания 3 из 14, мы находим, что 3 "входит" в 14 четыре раза, и еще "остается" число 2, т.е.

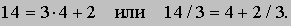
Число 14 называется делимым, число 3 - делителем, число 4 - частным и число 2 - остатком. Словами получившееся соотношение можно выразить так: делимое = (делитель ґ частное) + остаток, где 0 Ј остаток < делитель. Чтобы найти частное и остаток от деления 1400 на 3 с помощью многократного вычитания 3, потребовалось бы затратить немало времени и труда. Процедуру можно было бы существенно ускорить, если сначала вычитать из 1400 по 300, затем из остатка по 30 и, наконец, по 3. После четырехкратного вычитания 300 мы получили бы в остатке 200; после шестикратного вычитания из 200 числа 30 остаток оказался бы равным 20; наконец, после шестикратного вычитания из 20 числа 3 мы получим остаток 2. Следовательно,

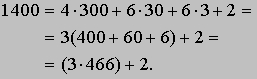
Частное и остаток, которые требовалось найти, равны, соответственно, 466 и 2. Вычисления можно организовать и затем последовательно подвергнуть сжатию следующим образом:

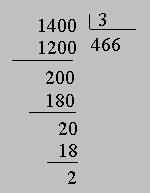
Приведенные выше рассуждения применимы, если делимое и делитель - любые положительные действительные числа, выраженные в десятичной системе. Проиллюстрируем это на примере 817,65/23,7. Сначала делитель с помощью сдвига десятичной запятой необходимо превратить в целое число. При этом десятичная запятая делимого сдвигается на такое же число десятичных знаков. Делитель и делимое располагаются, как показано ниже:

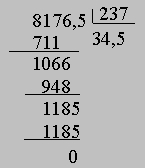
Определим, сколько раз делитель содержится в трехзначном числе 817, первой части делимого, которую мы делим на делитель. Так как по оценкам он содержится три раза, мы умножаем 237 на 3 и произведение 711 вычитаем из 817. Разность 106 меньше делителя. Это означает, что число 237 входит в пробное делимое не более трех раз. Цифра 3, написанная под цифрой 2 делителя ниже горизонтальной черты, - первая цифра частного, которое требуется найти. После того, как мы снесем вниз следующую цифру делимого, получится следующее пробное делимое 1066, и надо определить, сколько раз делитель 237 укладывается в числе 1066; предположим, что 4 раза. Умножаем делитель на 4 и получаем произведение 948, которое вычитаем из 1066; разность оказывается равной 118, что означает, что следующая цифра частного равна 4. Затем мы сносим следующую цифру делимого и повторяем всю процедуру, описанную выше. На этот раз оказывается, что пробное делимое 1185 точно (без остатка) делится на 237 (остаток от деления наконец оказывается равным 0). Отделив десятичной запятой в частном столько же знаков, сколько их отделено в делимом (напомним, что ранее мы десятичную запятую переносили), получим ответ: частное равно 34,5.

Дроби. Вычисления с дробями включают сложение, вычитание, умножение и деление, а также упрощение сложных дробей. Сложение дробей с одним и тем же знаменателем производится путем сложения числителей, например, 1/16 + 5/16 + 7/16 = (1 + 5 + 7)/16 = 13/16. Если дроби имеют различные знаменатели, то предварительно их необходимо привести к общему знаменателю, т.е. превратить в дроби с одинаковыми знаменателями. Для этого мы находим наименьший общий знаменатель (наименьшее число, кратное каждому из данных знаменателей). Например, при сложении 2/3, 1/6 и 3/5 наименьший общий знаменатель равен 30:

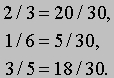
Суммируя, получаем 20/30 + 5/30 + 18/30 = 43/30. Вычитание дробей производится так же, как их сложение. Если знаменатели одинаковы, то вычитание сводится к вычитанию числителей: 10/13 - 2/13 = 8/13; если дроби имеют различные знаменатели, то предварительно необходимо привести их к общему знаменателю: 7/8 - 3/4 = 7/8 - 6/8 = (7 - 6)/8 = 1/8. При умножении дробей их числители и знаменатели умножаются отдельно. Например, 5/6*4/9 = 20/54 = 10/27. Чтобы разделить одну дробь на другую, необходимо умножить первую дробь (делимое) на дробь, обратную второй (делителю) (чтобы получить обратную дробь, надо поменять местами числитель и знаменатель исходной дроби), т.е. (n1/d1)/(n2/d2) = (n1*d2)/(d1*n2). Например, (3/4)/(7/8) = (3/4)*(8/7) = 24/28 = 6/7. Смешанное число представляет собой сумму (или разность) целого числа и дроби, например, 4 + 2/3 или 10 - 1/8. Так как целое число можно рассматривать как дробь с знаменателем, равным 1, смешанное число есть не что иное, как сумма (или разность) двух дробей. Например, 4 + 2/3 = 4/1 + 2/3 = 12/3 + 2/3 = 14/3. Сложной называется дробь, имеющая дробь либо в числителе, либо в знаменателе, либо в числителе и знаменателе. Такую дробь можно превратить в простую:

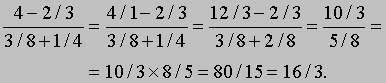
Квадратный корень. Если n - положительное действительное число, то существует единственное положительное действительное число r, такое, что r2 = n. Число r называется квадратным корнем из n и обозначается . В школе учат извлекать квадратные корни двумя способами. Первый способ более популярен, поскольку он проще и его легче применять; вычисления по этому методу легко реализуются на настольном калькуляторе и обобщаются на слу

Составить слова из слова арифметика

ХУДОЖЕСТВЕННЫЙ СТИЛЬ РЕЧИ, ИЛИ ХУДОЖЕСТВЕННО-ИЗОБРАЗИТЕЛЬНЫЙ, ХУДОЖЕСТВЕННО-БЕЛЛЕТРИСТИЧЕСКИЙ - один из функциональных стилей (см.), характеризующих тип речи в эстетической сфере общения: словесных произведений искусства. Конструктивный принцип Х. с. р. - контекстуальный "перевод" слова-понятия в слово-образ; специфическая стилевая черта - художественно-образная речевая конкретизация (см.).

Несмотря на особенную значимость для худож. произведения проявления в нем авторской индивидуальности, несмотря на многообразие направлений, методов и жанров худож. литературы, последняя, однако, имеет общий для всех их принцип использования языка, обусловленный назначением искусства в обществе, образным мышлением художника в процессе творчества, эстетической функцией. Здесь слово-понятие языка (понятийная сущность слова) как бы переводится средствами контекста в слово-образ (в широком смысле) для выражения образной мысли автора и изображаемой им вымышленной действительности. Реализация эстетической функции языка в худож. сфере общения составляет специфику худож. речи - всех ее индивидуально-авторских стилей и жанров, при всем их своеобразии и отличиях.

Вопрос о стилевом статусе худож. речи (несинонимичный термин - "язык художественной литературы" - см.) среди функц. стилей считается дискуссионным. Имеются две точки зрения: 1) правомерность выделения среди функц. стилей Х. с. р.; 2) категорическое неприятие такой точки зрения. Первое положение разделяют В.В. Виноградов, Р.А. Будагов, И.Р. Гальперин, Б.Н. Головин, Э.Г. Ризель, К.А. Долинин, М.Н. Кожина, О.Б. Сиротинина, Й. Мистрик, К. Гаузенблас, М. Елинек и мн. др. Второе - Л.Ю. Максимов, А.К. Панфилов, Н.А. Мещерский, Д.Н. Шмелев, В.Д. Бондалетов и др.

Аргументами против признания возможности выделять среди функц. стилей и художественный являются: 1) так называемая многостильность худож. литературы, использование в ней языковых средств разных (всех) функц. стилей; 2) отсутствие специфических языковых примет (средств), свойственных именно худож. речи (худож. текстам); 3) наличие у худож. речи особой эстетической функции; 4) неправомерность объединения понятий "литературный язык" и "язык художественной литературы".

Однако характерно, что в этой аргументации и ее конкретизации представители указанной (второй) точки зрения обычно исходят в своем анализе не из теоретических положений функц. стилистики (как учения о функц. стилях, принципа их классификации), а из постулатов "стилистики ресурсов" (см.), т.е. стилистики языковых единиц без учета речевой системности стиля, критериев определения функц. стиля.

С функциональной точки зрения нельзя говорить о многостильности худож. лит-ры, так как использование отдельных языковых средств других функц. стилей не определяет тот или иной функц. стиль, главное, как используются эти средства и каковы их стилистические функции, в какой речевой организации они выступают. Наблюдения показывают, что языковые средства других стилей (напр. научные термины, фразеология делового стиля) используются в худож. речи не в их основной, а в измененной функции (в соответствии с целью и задачами общения в эстетической сфере), т.е. изобразительно-выразительной, в эстетической функции (при этом в выборе средств все же есть свои ограничения, например не вся известная терминология науки представлена в худож. текстах). Тем самым в худож. речи могут использоваться языковые средства других стилей, но не сам стиль как таковой, с присущей ему речевой системностью и, главное, не в той же функции. Ср. употребление терминов в поэтической речи: И я из дома убежал, чтоб наконец-то выбраться из радиуса действия обыденной любви; Есть радиусы действия у гнева и у дерзости; Есть радиусы действия у правды и у лжи (Р. Рождественский); Сошли с ума муссоны и пассаты (В. Маяковский). Еще пример более широкого контекста, показывающего принципиальное отличие стиля худож. прозы от научной при описании одного и того же явления природы писателем и ученым:

По народной примете, лес притягивает воду, чтобы затем отпустить ее облачком в дальнейшее странствие. Значит, он каждую каплю воды впрягает в двойную и тройную работу. Чем больше леса, тем чаще прикоснутся дождичком к земле те постоянные двести миллиметров осадков, что в среднем получаем из океана в год… Лес приближает море, и сам как море, корабли туч ночуют у его зеленых причалов… (Л. Леонов. Русский лес)

При изучении роли леса в круговороте воды возникают два основных вопроса: а) какова роль леса как фактора образования осадков и б) какова роль в распределении осадков, выпадающих из атмосферы?.. Лес, образуя огромную охлаждающую поверхность… содействует конденсации паров… При выпадении осадков в лесу часть их задерживается кронами и путем физического испарения возвращается в атмосферу (М.Е. Ткаченко. Общее лесоводство)

Таким образом, с точки зрения функциональной, многостильности (в точном смысле слова) в художественных текстах нет.

Далее, не только худож., но никакой другой функц. стиль не создается совокупностью каких-либо специфических языковых средств (тем более одной окраски); они лишь часть (и не главная) стилевой специфики того или иного функц. стиля. Наличие же эстетической функции у худож. речи как раз и составляет ее специфику, на основе которой следует выделять худож. речь в особую функц.-стилевую разновидность (как это делается в отношении других функц. стилей с учетом принципа их классификации); это один из существенных стилеобразующих признаков функц. стиля. Следовательно, наличие специфики у худож. текстов в виде эстетической функции служит аргументом не против отнесения этого типа речи к функц. стилям, а за включение его в эту систему (ср.: в научном - речевая экспликация познавательно-коммуникативной функции; в оф.-деловом - коммуникация через предписующе-долженствующую установку деонтического мышления и т.д.).

По вопросу соотнесения понятий "литературный язык" и "язык художественной литературы" следует сказать, что они безусловно не тождественны. "Язык художественной литературы" - это одна из разновидностей лит. языка, т.е. эти понятия соотносительны как общее, родовое, и видовое. Использование языка в эстетической функции не превращает его в какую-то новую субстанцию, не аннулирует его коммуникативной функции (напротив, эстетическая функция существует на базе коммуникативной). Язык, представленный в худож. текстах, является образцом лит. языка (общенародный язык шлифуется и обрабатывается в "лабораториях" писателей), поэтому он широко используется в качестве иллюстративного материала в грамматиках и словарях. Очень удачно по затронутому вопросу выразился Ю.А. Бельчиков: "Язык художественной литературы, будучи явлением искусства, не утрачивает своей лингвистической субстанции", он "обязательно ориентирован на нормы литературного языка". Нельзя забывать, что "эстетическая функция - это функция языковая" (Д.Н. Шмелев). Таким образом, функциональная стилистика не отождествляет понятия "литературный язык" и "язык художественной литературы", различает их, соотносит, но не разрывает как две совершенно разные сущности.

Очевидно, при рассмотрении вопроса о стилевом статусе худож. речи следует иметь в виду то, что худож. тексты как сложный объект исследования могут изучаться в разных аспектах: в собственно лингвистическом (как образцы лит. языка), как ресурсы стилистических средств языка; в функц.-стилистическом - как Х. с. р.; в лингво-литературоведческом - как воплощение в тексте идейно-образного содержания, замысла художника слова, когда термин "язык художественной литературы" понимается как элемент формы (или материала) словесного произведения искусства. Необходимо четко различать эти аспекты, не смешивать и не подменять понятия одного из аспектов другим, что, к сожалению, наблюдается в литературе вопроса. Каждый из этих аспектов (и точек зрения) сам по себе имеет право на существование. Трудности же и недоговоренность в решении затронутого вопроса связаны как раз с неразличением и смешением этих аспектов. Так, вкрапления в худож. текст отдельных языковых единиц из других функц. стилей можно назвать многостильностью только с позиций стилистики ресурсов; с точки же зрения функц. стилистики в этом случае нет многостильности, поскольку функц. стиль создается не совокупностью (не суммой) стилистически маркированных единиц, а специфической в каждом из них речевой организацией (системностью). Далее. Справедливо мнение, что "материалом" всех текстов является язык, но… только в художественной сфере языковые средства сами по себе служат созданию произведений искусства" (Шмелев Д.Н., 1989; выделено нами. - М.К.). Тем самым можно говорить о "языке" в худож. произведении как факте искусства, но, во-первых, четко осознавать особое положение этого исследовательского аспекта, не позволяющего с его позиций решать вопросы функц. стилистики (т.е. стиль или не стиль худож. речь?); во-вторых, все же совсем не отрываться от лингвистики, памятуя, что исходить анализ худож. литературы "может, конечно, только из чисто словесного, лингвистического состава произведения, однако не должен и не может замыкаться в его пределах…" (Бахтин М.М., 1995, с. 21; выделено нами. - М.К.). Показательно, что Д.Н. Шмелев, в одной из своих последних работ "смягчивший" категоричность прежних взглядов по затронутому вопросу, отмечает, что "эстетическая функция объединяет все виды словесных художественных произведений" (Шмелев Д.Н., 1989, с. 22). Именно она и определяет принципы и закономерности речевой организации худож. произведений, создавая их специфику, отличную от других функц. стилей. Это самая общая (инвариантная) черта худож. речи, не препятствующая, однако, проявлению индивидуально-авторского и жанрового многообразия худож. литературы.

Как выход из создавшейся ситуации в отношении рассматриваемого вопроса С. Сятковский предлагает: "…введение в научный обиход понятия художественного стиля, понимаемого как генотип (инвариант) по отношению к фенотипической (вариативной) природе языка художественных произведений" (Сятковский С., 1995, с. 222). Однако функц. стилистика как раз и определяет функц. стиль как инвариант, реализуемый множеством различных вариантов, но, видимо, это положение не стало аксиоматичным у стилистов. Далее автор продолжает, что высказанное им предложение "…имело бы для стилистики художественной литературы приблизительно то же значение, как в свое время различение в фонетике фонемного и звукового уровней" (Там же).

И все же вопрос о статусе худож. речи среди функц. стилей требует оговорки: в силу функц. осложненности худож. речи, последняя, бесспорно "обладая" статусом функц. стиля, занимает особое положение среди других функц. стилей (как и - по другим причинам - разг. речь). Есть основания принять такую известную в стилистике классификацию функц. стилей: худож. речь - нехудож. (специальная), представленная стилями: научным, оф.-деловым, газетно-публиц., - обиходно-разговорная. Кстати, такая схема представлена в чехословацкой стилистике.

Итог рассматриваемому вопросу убедительно подведен К.А. Долининым: "Долго спорили о том, существует ли в современных европейских языках функциональный стиль художественной литературы… Ясно, что если толковать функциональные стили как нормы речевого построения текстов различных жанров, то нет никаких препятствий для того, чтобы рассматривать в ряду других функциональных стилей и стиль художественной литературы в целом, несмотря на его стилистическую неоднородность… И если мы решаем, что функциональный стиль выделяется на основе сферы деятельности, которую он обслуживает, и основной функции… (а все функциональные стили выделяются именно так), то сложность и неоднородность его состава не должны нас останавливать…" (Долинин К.А., 1978, с. 66-67).

В худож. речи употребляются все известные стилистические ресурсы русского языка. Ей свойственны широкая и глубокая метафоричность, богатая синонимика, многозначность, разнообразие стилевых пластов лексики и др. При этом в каждом конкретном случае из всего арсенала языково-стилистических средств уместным, единственно необходимым в данном контексте оказывается лишь одно, избранное средство (имеются в виду высокоэстетические худож. произведения). В понятие высоких качеств худож. речи и непременных ее свойств входят неповторимость и свежесть выражения при создании образов, яркая их индивидуальность. Кроме того, худож. стиль отличается не только образностью, но и явной эмоциональностью, в целом - эстетически направленной экспрессивностью.

Говоря о лингвостилистических чертах худ. речи, прежде всего следует отметить особую жизнь слова в худож. произведении. Его (слова) специфической особенностью является актуализация внутренней формы (Г.О. Винокур), когда средства языка, в частности лексические, и их значения оказываются той основой, отталкиваясь от которой художник создает поэтическое слово-метафору, целиком "повернутую" к теме и идее конкретного худож. произведения. При этом метафорическое значение слова нередко может быть понято и определено лишь по прочтении всего произведения, т.е. вытекает из худож. целого. Так, по наблюдению Г.О. Винокура, смысловое значение слова хлеб, поставленного в заглавие романа А. Толстого, означает не то же, что общеизвестное значение этого существительного. Но, опираясь на него и отталкиваясь от него, это слово получает в контексте худож. целого способность выражать одно из явлений революции и гражданской войны, представленное в романе (Винокур Г.О., 1959, с. 391).

Формирование значения худож. слова в широком контексте целого произведения отмечал Б.А. Ларин. Он же выявил системную взаимосвязь слова с другими словами худож. целого при выражении сквозной поэтической мысли-идеи, т.е. лейтмотива произведения. Такое свойство поэтического слова Б.А. Ларин называет "комбинаторными приращениями смысла".

Понятия внутренней формы худож. слова и комбинаторных приращений смысла тесно связаны с понятием "общей образности" (А.М. Пешковский), которая заключается в том, что все языковые единицы того или иного худож. произведения направлены на выражение худож. образа, являясь в то же время строго эстетически и стилистически мотивированными и оправданными, в связи с чем устранение из текста какого-либо одного слова уже ведет к "облысению" образа (выражение А.М. Пешковского). То же касается и видоизменения форм слова, что ярко показано Г.О. Винокуром на примере невозможности изменения слова рыбка на рыба в заглавии и тексте пушкинской "Сказки о рыбаке и рыбке".

По В.В. Виноградову, худож. слово принципиально двупланово. Совпадая по своей форме со словом национального языка и опираясь на его значение, худож. слово обращено не только к общенародному языку, но и к тому миру худож. действительности, который создается или воссоздается в произведении. Смысловая структура слова "расширяется и обогащается теми художественно-изобразительными "приращениями", которые развиваются в системе целого эстетического объекта" (Виноградов В.В., 1963, с. 125).

Более общим, точнее, инвариантным - с указанием причин явления, - оказывается понятие художественно-образной речевой конкретизации (см.) (Кожина М.Н., 1966), т.е. системной взаимосвязи языковых единиц как составных элементов целого, обусловленной идейно-образным содержанием и реализующей эстетическую функцию в результате "перевода" слова-понятия в слово-образ, направленного на активизацию воображения читателя. Причем это реализуется именно в условиях специальной речевой организации: не только за счет связей близко расположенных языковых единиц, как правило, отличающихся индивидуальностью и неповторимостью их сочетаний, но и дистантно расположенных, т.е. как узкоконтекстных, так и ширококонтекстных. Важно, что в создании и выражении специфики худож. стиля, в реализации эстетической функции языка, в способах худож.-образной речевой конкретизации большую роль играют не только стилистически окрашенные, но и нейтральные языковые средства, которые приобретают новые качества, становятся элементами искусства. Истинный мастер способен придать любой лингвистической единице в контексте худож. произведения эстетическое "звучание" и значимость.

Проиллюстрируем сказанное фрагментом из "Капитанской дочки" А.С. Пушкина: Урядник привел меня в избу, стоявшую на высоком берегу реки, на самом краю крепости… Савельич стал в ней распоряжаться; я стал глядеть в узенькое окошко. Передо мною простиралась печальная степь. Наискось стояло несколько избушек; по улице бродило несколько куриц. Старуха, стоя на крыльце с корытом, кликала свиней, которые отвечали ей дружелюбным хрюканьем. И вот в какой стороне осужден я был проводить свою молодость! Этот небольшой отрывок из нескольких предложений представляет весьма яркую образную картину и той обстановки отдаленной маленькой крепости, в которой очутился молодой Гринев, и его настроение и переживания в связи с назначением в эту глухую сторону. Несмотря на то что здесь почти отсутствуют тропы, создается отчетливый зрительно-психологический образ. Этому способствует лаконизм выражения, отбор точных и емких, к тому же единичных и тем самым более выразительных определений (узенькое окошко, печальная степь, несколько избушек, несколько куриц, дружелюбное хрюканье). Последняя фраза с ее порядком слов, их отбором (осужден и вот в какой стороне…), восклицательной интонацией представляет собой как бы крик души юного офицера, охваченного тоской.

Таким образом, худож. произведение способно преобразовывать семантику любого, в том числе и нейтрального, слова, наделяя ее текстовыми приращениями смысла, прежде всего эмоционально-экспрессивными и эстетическими, что достигается, в частности, повторением лексической единицы в разных контекстах. С этим связано проявление такой важной черты текстовой семантики худож. произведения, как динамичность смысла (Виноградов В.В., 1963, с. 162). Многократное предицирование повторяющейся номинации приводит к присоединению каждого нового признака к предыдущим и формированию более сложного по сравнению с языковым текстового смысла. Данное явление носит типичный характер и обладает большой значимостью, так что некоторые исследователи предлагают даже выделять особый тип лексического значения - "художественное значение" (Барлас Л.Г., 1982). Слово с худож. значением - это элемент текста, значимый для более глубоких смысловых слоев худож. текста - образного и идейного (Купина Н.А., 1983). Специфической чертой функционирования языковых средств в худож. стиле является также преобладание смысла слова над его значением, что приводит к созданию имплицитного идейно-эстетического содержания произведения (подтекста), требующего специальной интерпретации.

Типичное явление худож. речи - метафоризация (в широком смысле). См. у А.С. Пушкина изображение гибели Ленского через символические ассоциации, метафорические отождествления: Мгновенным холодом облит, / Онегин к юноше спешит, / Глядит, зовет… / Его уж нет. Младой певец / Нашел безвременный конец! / Дохнула буря, цвет прекрасный / Увял на утренней заре, / Потух огонь на алтаре! Ср. также в прозаическом произведении выражение внутренней жизни героя, его психического состояния через изображение движения, жеста посредством образного сравнения (о Каренине в "Анне Карениной"): Он не спал всю ночь, его гнев увеличивался. Он оделся и, как бы неся полную чашу гнева и боясь расплескать ее… вошел к ней. Н.А. Кожевникова разграничивает следующие типы метафор: общеязыковые, напр.: Потом вспыхнула и поглядела на часы (Чехов); метафоры-сравнения, напр.: Волнистый дым рубашки пеленал ее тело (Белый); метафоры-загадки, напр.: Сквозной лебедь в окне там поплыл над хрустальным ледком - о метели (Белый); антропоморфные метафоры: …И вдруг вся широкая степь сбросила с себя утреннюю полутень, улыбнулась и засверкала росой (Чехов) и др. (Кожевникова Н.А., 1994, с. 176-188).

Весьма специфичны для худож. текстов и такие случаи, когда какое-либо слово становится лейтмотивом произведения, выражая определенную идейно-образную "линию" повествования. Таковы, например, в "Русском лесе" Л. Леонова сквозные образы реки, воды как символов жизни или ле́са, лесного сообщества, ассоциативно передающие сложные взаимоотношения изображаемых в романе персонажей.

Характерно для худож. речи и то, что слово - причем обычное, нейтральное слово, - вовлекаясь в эстетическую организацию речи, не просто наполняется новым содержанием, но как средство материализации образного смысла становится элементом идейно-художественного целого, оказывается способным передавать глубокое содержание. Так, по наблюдениям Д.Б. Благого в "Медном всаднике" А.С. Пушкина контраст "общего" и "частного", конфликт между ними, передающий основной идейный смысл поэмы, подчеркивается композиционным противопоставлением разных форм личных местоимений. О Петре: Отсель грозить мы будем шведу; Природой здесь нам суждено / В Европу прорубить окно; Все флаги в гости будут к нам. О Евгении: О чем же думал он? О том, / Что был он беден, что трудом / Он должен был себе доставить / И независимость, и честь, / …И что с Парашей будет он / Дни на два, на три разлучен.

Итак, все, что выражено в произведении, выражено через посредство слова (языка) - именно в этом смысле "язык есть первоэлемент литературы" (М. Горький). Но не все, выраженное в нем, выражено непосредственно словом. Например, по наблюдениям А.Н. Васильевой, в "Воскресении" Л. Толстого параллельно описывается тюремное утро Катюши Масловой и сибаритское утро Нехлюдова, и этот контрастирующий параллелизм рождает в читателе много мыслей и чувств, прямо не выраженных в слове. В "Тоске" А.П. Чехова прямо не сказано, что чувство тоскливого одиночества особенно угнетающе действует на Иону в окружении суетящейся многочисленной толпы занятых только собой людей, но писатель изображает тоскующего одинокого человека на фоне этой толпы, и прямо не выраженная мысль художника становится понятной читателю (Васильева А.Н., 1983, с.136). Значит, выбор ситуации, события, персонажей, пейзажа, интерьера, фактических деталей, поступков, жестов, мимики героя, их композиционное расположение и т.д. - все эти "затекстовые" компоненты худож. стиля оказывают влияние на функционирование языковых средств в произведении и сами испытывают их влияние. В структуре произведения все они составляют единое целое, единственное в своем качестве, неразрывное, и только в целом проявляют свои высшие идейно-эстетические функции.

Худож. текст характеризуется выверенным соотношением пропорций. В нем, как и в других видах искусства, эстетической ценностью обладают различные проявления симметрии, выражающиеся в приемах организации ритма, фоники и интонации, композиции (см.), архитектоники и др., - в целом, форма произведения. Более того, "изменение, ломка формы художественного текста приводит к разрушению содержания его, искажению идеи" (Одинцов В.В., 1980, с. 161). По мнению В.В. Виноградова, "…В композиции художественного произведения динамически развертывающееся содержание раскрывается в смене и чередовании разных форм и типов речи, разных стилей, синтезируемых в "образе автора" и его создающих как сложную, но целостную систему экспрессивно-речевых средств. Именно в своеобразии этой речевой структуры образа автора глубже и ярче выражается стилистическое единство композиционного целого" (Виноградов В.В., 1959, с. 154).

В основе композиции худож. произведения лежит тот или иной худож. прием - семантико-стилистический стержень, вокруг которого организовано содержание. Причем иерархическая упорядоченность в худож. структуре носит принципиально иной характер по сравнению со структурой делового, научного и прочих текстов. Если в нехудож. текстах композиция определяется характером логических отношений элементов, то в худож. тексте она индивидуальна и неповторима. Ср.: "Сколько ни изучай компоненты художественного произведения, - невозможно понять их смысл, всех в совокупности и каждого порознь, если не поймешь общего, единого и все в произведении пронизывающего идейного устремления и художественного принципа, являющегося основой эстетического бытия произведения" (Гуковский Г.А., 1966, с. 109).

Детальный анализ типов композиции представлен в работе В.В. Одинцова (1980). Разделяя точку зрения Л.С. Выготского относительно того, что "…в художественном произведении всегда заложено некоторое противоречие, некоторое внутреннее несоответствие между материалом и формой…" (Выготский Л.С., 1968, с. 208), В.В. Одинцов, в частности, исследует композиционный прием контраста, как типичный способ преодоления отмеченного "противоречия". В качестве иллюстрации автор анализирует рассказ Л. Толстого "После бала", в котором противопоставлены две части: I. Бал (любовь Ивана Васильевича к Вареньке, ее отец-полковник в танце с дочерью) и II. После бала (на глазах рассказчика - Ивана Васильевича - страшная сцена экзекуции над солдатом, которой руководит полковник, отец Вареньки; сцена, перевернувшая жизнь Ивана Васильевича) (Одинцов В.В., указ. соч., с. 168-171. См. также: Кожина М.Н., 1993, с. 212-213). В этих двух сценах все повествование построено на контрасте, что и выражается в отборе и употреблении слов определенной семантики. Так, в описании бала большую роль играют эмоциональные определения, эпитеты (Бал был чудесный; зала прекрасная; буфет великолепный; восторженное, нежное чувство; ласковые, милые глаза и др.), попарное объединение слов (выразить весь свой восторг и благодарность, в знак сожаления и утешения, все смотрели на нее и любовались ею) и др. В этой сцене состояние души Ивана Васильевича переполнено любовью, восхищением и нежностью, ведь это была самая сильная любовь его; он был сильно влюблен; счастлив, блажен… добр. Вся эта сцена рисуется в светлых, радостных тонах, окрашенных словами-образами любви, улыбки, умиления.

Совершенно иные средства использованы в сцене экзекуции, которая изображается в мрачных, темных тонах и неприятных звуках. Сами по себе нейтральные слова, а также лексемы эмоциональной семантики, их нагнетение в тексте (в противоположность "светлым" словам первой части рассказа) оказываются весьма эстетически значимыми. Единичные определения здесь предметны (скользкая дорога, белые зубы, черные мундиры, черные люди) и использованы для достижения контраста. Причем контраст создают как антонимичные прилагательные (белый - черный), так и те, на первый взгляд нейтральные, предметные, которые уже использовались при описании бала и вновь повторяются, но уже в иных условиях, в ином окружении - при описании экзекуции, см.: Это был ее отец, с своим румяным лицом и белыми усами и бакенбардами. Во второй части меняется и грамматический характер определений (это преимущественно страдательные причастия: оголенный по пояс человек, привязанный к ружьям, под сыпавшимися ударами, подрагивающей походкой, сморщенное от страданий лицо и др.), а также изложения в целом: если в описании бала доминируют прилагательные, то в описании экзекуции - глаголы. Композиция рассказа, построенная на контрасте, а вместе с тем и особая организация речи, наполненная лексикой также контрастного значения, усиливает, подчеркивает не только зримые образы, но и чувства, переживания и тем самым передает идею произведения. Кроме того, языковые черты второй части рассказа свидетельствуют об изменении точки зрения повествователя: сквозь объективно-повествовательный тон рассказчика прорывается голос непосредственного наблюдателя экзекуции. Хотя повествование по-прежнему ведется от лица Ивана Васильевича, говорит уже не тот человек, для которого изображаемое стало далеким прошлым; говорит человек, который все это видит впервые и еще не знает точно, что происходит. Так углубляется намеченное в начале противопоставление. Содержательный контраст усиливается контрастом стилистическим. Усиление, углубление контраста осуществляется благодаря тому, что конструируется новая субъектная сфера - герой, непосредственный наблюдатель происходящего; изображаемое пропускается через призму его сознания. Соотношение "автор - рассказчик" (сцена бала) осложняется при описании сцены "после бала": "автор" - "рассказчик" - "герой" (непосредственный наблюдатель). Стилистический эффект подобного усложнения композиции отмечал В.В. Виноградов: "Изображение событий с точки зрения непосредственного наблюдателя усиливает и подчеркивает реалистический "тон" и стиль воспроизводимых сцен, создавая иллюзию прямого отражения действительности. Несмотря на субъективную призму персонажа, и именно благодаря ей, возрастает "объективная" точность, достоверность изображения" (Виноградов В.В., 1939, с. 172).

Одним из типичных способов развертывания худож. текста являются повторы - звуковой, лексический, словообразовательный, синтаксический и др. Как подчеркивает Н.А. Кожевникова (1994), важнейшая роль в организации текста принадлежит словесному повтору, чрезвычайно разнообразному по языковой реализации (от слова до сложного синтаксического целого) и выполняемым функциям. Во-первых, повторяющееся слово эксплицирует тему определенного фрагмента текста или целого произведения. Например, в рассказе Л. Андреева "В тумане" слово туман проходит и через речь автора, и через речь персонажей. Во-вторых, повторы последовательно используются при характеристике персонажей: внутренняя определенность и замкнутость образа создается повтором детали, повтором устойчивого признака, который используется и как характеристика персонажа вообще, и как характеристика отдельных его черт. Более того, повторяющийся эпитет нередко распространяется на предметы, окружающие персонажа. Так, в повести Н. Лескова "Смех и горе" таким способом характеризуется голубой купидон - жандармский капитан Постельников, появление которого подготовлено изображением интерьера: светло-голубые, небесного цвета стены, вся эта мебель обита светлым голубым ситцем, голубые ситцевые занавески, с подзорами на окнах, и дорогой голубой шелковый полог над широкою двуспальною постелью. На этом фоне рассказчик видит какое-то голубое существо - таки все-все сплошь голубое: голубой воротник, голубой сюртук, голубые рейтузы… В-третьих, повтор слова или фразы передает мысль, оценку и навязчивую идею персонажа (см., фразу Беликова Как бы чего не вышло из "Человека в футляре" Чехова).

Повторяющиеся детали связывают разные эпизоды текста, устанавливая между ними точки соприкосновения. Так, в "Отце Сергии" Л. Толстого в сцене объяснения Касатского с невестой акцентирована деталь - пение соловья: Соловей защелкал вблизи. Эта же деталь повторяется затем в сцене, предшествующей падению отца Сергия: Соловьи, одни совсем близко, и другие два или три внизу в кустах у реки, щелкали и заливались. Таким образом, посредством повтора замыкается некоторое сюжетное кольцо произведения.

В качестве разновидности повтора, характерной для литературы ХХ в., Н.А. Кожевникова называет монтаж развернутых фрагментов текста из отрезков, использованных ранее, когда новый контекст возникает как комбинация элементов одного исходного контекста (подробнее см.: указ. соч., с. 196-198).

Нередко в худож. произведении возникают образные поля, основанные на сквозном повторе, который проходит через весь текст, устанавливая ряды регулярных образных соответствий. Так, для произведений Л. Толстого характерно противопоставление образных полей "свет - тьма", "огонь - холод" ("Анна Каренина", "Смерть Ивана Ильича" и др.). В романе И. Гончарова "Обломов" развертываются образные параллели "жизнь - река", "жизнь - цветение" и др. "Особенность образных полей, - считает Н.А. Кожевникова, - заключается в том, что повторяющиеся образные характеристики связаны не только с ведущими темами текста, но и присутствуют на периферии, распространяясь на предметы, внешне далекие от развития центральных линий" (там же, с. 213). Наконец, повтор играет существенную роль в композиционном развертывании произведения, обеспечивая кольцевую композицию.

В целом, композиционно-стилистическая организация худож. произведения является важным средством реализации его идейно-эстетического содержания. При этом важно, что каждое худож. произведение представляет собой единство композиционно-стилистической структуры, т.е. целостную стилистическую систему, объединенную образом автора (см.). Автор так строит свой текст, так расставляет акценты, так группирует и соотносит различные моменты изображения, что добивается нужного впечатления, нужного воздействия на читателя. Авторский угол зрения пронизывает и скрепляет все произведение и объясняет место, роль и функцию каждого его худож. элемента.

Х. с. р. предполагает существование индивидуальных стилей, без которых худож. литература вообще немыслима. Худож. речь и формируется как собственно функц. стиль лит. языка именно тогда, когда формирование самого этого языка как единого национального дает основу для широкого стилистического проявления творческой индивидуальности писателя (см. Идиостиль, индивидуальный стиль, идиолект).

Однако при всех неповторимо-индивидуальных лингвостилистических особенностях отдельных произведений худож. речь в целом имеет общие принципы отбора и закономерности функционирования языковых единиц, обусловленные реализацией эстетической функции. Это ярко выражается, например, в значениях и функционировании времен и видов глаголов (см. М.Н. Кожина, 1966, 1972). Для худож. речи характерно использование форм прош. времени в связи с повествовательной манерой изложения. Наст. время нередко используется в значении настоящего исторического (настоящего живого представления). Разнообразны и значения буд. времени. Широко представлено переносное употребление времен и многообразие их значений, при этом преобладают наиболее конкретные значения. В связи с этим настоящее вневременное, свойственное научной речи как наиболее отвлеченное, в худож. стиле встречается редко. В Х. с. р. преобладает использование сов. вида глагола как более конкретного сравнительно с несов. видом. Формы несов. вида отличаются многообразными видовыми оттенками, конкретизирующими выражение характера действия, чего не наблюдается, например, в науч. речи.

Весьма характерно также и то, что изложение обычно охватывает не какой-либо один видовременной план, а разные. Этим создается бoльшая выразительность, динамизм повествования. Например: Вижу я, как на мелком месте текущая вода встречает преграду, вода устремляется в узкую приглубь, и от этой бесшумной устремленности вот и кажется, будто вода мускулы сжала, а солнце это подхватывает… А вот большой завал, и вода как бы ропщет. Но это не слабость, не жалоба, не отчаяние, вода этих чувств вовсе не знает, каждый ручей уверен в том, что добежит до свободной воды… Дерево давно и плотно легло на ручей… но ручей нашел себе выход под деревом и быстриком, с трепетными тенями бьет и журчит (Пришвин). Глаголы различных семантических групп выступают здесь именно в образно-конкретизирующей функции благодаря отбору слов и особому контекстному окружению. В целом худож. стиль характеризуется высокой частотностью глаголов и особой ролью этой части речи в достижении образной конкретизации. Благодаря глагольному речеведéнию (термин М.Н. Кожиной), писатель активизирует читательское воображение, создавая поэтапное представление о худож. образе.

В Х. с. р. преобладают конкретные существительные. Абстрактные слова приобретают конкретно-образное значение благодаря метафоризации, напр.: Тогда обрадованная мысль летает от одного солнечного пятна к другому (Пришвин); Расплескал злобу в драке с Петром (Шолохов); Смерть как будто заигрывала с казаком (Шолохов). Формам числа существ. также свойственны наиболее конкретные значения: в ед. числе - указание на отдельные считаемые предметы, во мн. числе - на совокупность, множество отдельных предметов.

Краткие прилагательные, в отличие от науч. стиля, в худож. речи обозначают обычно состояния и признаки героя (предмета, явления) в определенный момент времени, напр.: На этот раз он был молчалив,

Составить слова из слова художественный стиль речи, или художественно-изобразительный, художественно-беллетристический