ж.
Раздел математики, изучающий качественные свойства геометрических фигур, не зависящие от их длины, величины углов, прямолинейности и т.п.
топология
Толковый словарь
Толковый словарь Ушакова
ТОПОЛО́ГИЯ, топологии, мн. нет, жен. (от греч. topos - место и logos - учение) (мат.). Часть геометрии, исследующая качественные свойства фигур (т.е. не зависящие от таких понятий, как длина, величина углов, прямолинейность и т.п.).
Энциклопедический словарь
ТОПОЛО́ГИЯ -и; ж. [от греч. topos - место и logos - учение] Раздел математики, изучающий наиболее общие свойства геометрических фигур, не изменяющиеся при любых деформациях.
◁ Топологи́ческий, -ая, -ое. Т-ие свойства фигуры. Т. факт.
* * *
тополо́гия (от греч. tópos - место и ...логия), раздел математики, изучающий топологические свойства фигур, то есть свойства, не изменяющиеся при любых деформациях, производимых без разрывов и склеиваний (точнее, при взаимно однозначных и непрерывных отображениях). Примерами топологических свойств фигур являются размерность, число кривых, ограничивающих данную область, и т. д. Так, окружность, эллипс, контур квадрата имеют одни и те же топологические свойства, так как эти линии могут быть деформированы одна в другую описанным выше образом; в то же время кольцо и круг обладают различными топологическими свойствами: круг ограничен одним контуром, а кольцо - двумя.
* * *
ТОПОЛОГИЯ - ТОПОЛО́ГИЯ (от греч. topos - место и logos - слово, учение), раздел математики, изучающий топологические свойства фигур, т. е. свойства, не изменяющиеся при любых деформациях, производимых без разрывов и склеиваний (точнее, при взаимно однозначных и непрерывных отображениях). Примерами топологических свойств фигур являются размерность, число кривых, ограничивающих данную область. Так, окружность, эллипс, контур квадрата имеют одни и те же топологические свойства, т. к. эти линии могут быть деформированы одна в другую описанным выше образом; в то же время кольцо и круг обладают различными топологическими свойствами: круг ограничен одним контуром, а кольцо - двумя.
Большой энциклопедический словарь
ТОПОЛОГИЯ (от греч. topos - место и ...логия) - раздел математики, изучающий топологические свойства фигур, т. е. свойства, не изменяющиеся при любых деформациях, производимых без разрывов и склеиваний (точнее, при взаимно однозначных и непрерывных отображениях). Примерами топологических свойств фигур являются размерность, число кривых, ограничивающих данную область, и т. д. Так, окружность, эллипс, контур квадрата имеют одни и те же топологические свойства, т. к. эти линии могут быть деформированы одна в другую описанным выше образом; в то же время кольцо и круг обладают различными топологическими свойствами: круг ограничен одним контуром, а кольцо - двумя.
Академический словарь
-и, ж.
Раздел математики, изучающий наиболее общие свойства геометрических фигур, не изменяющиеся при любых деформациях.
[От греч. τόπος - место и λόγος - учение]
Энциклопедия Кольера
ТОПОЛОГИЯ - раздел математики, занимающийся изучением свойств фигур (или пространств), которые сохраняются при непрерывных деформациях, таких, например, как растяжение, сжатие или изгибание. Непрерывная деформация - это деформация фигуры, при которой не происходит разрывов (т.е. нарушения целостности фигуры) или склеиваний (т.е. отождествления ее точек). Такие геометрические свойства связаны с положением, а не с формой или величиной фигуры. В отличие от евклидовой и римановой геометрий, геометрии Лобачевского и других геометрий, занимающихся измерением длин и углов, топология имеет неметрический и качественный характер. Раньше она носила названия "анализ ситус" (анализ положения), а также "теория точечных множеств". В научно-популярной литературе топологию часто называют "геометрией на резиновом листе", поскольку ее наглядно можно представлять себе как геометрию фигур, нарисованных на идеально упругих резиновых листах, которые подвергаются растяжению, сжатию или изгибанию. Топология - один из новейших разделов математики.
История. В 1640 французский математик Р.Декарт (1596-1650) нашел инвариантное соотношение между числом вершин, ребер и граней простых многогранников. Это соотношение Декарт выразил формулой V - E + F = 2, где V - число вершин, E - число ребер и F - число граней. В 1752 швейцарский математик Л. Эйлер (1707-1783) дал строгое доказательство этой формулы. Еще один вклад Эйлера в развитие топологии - это решение знаменитой задачи о кенигсбергских мостах. Речь шла об острове на реке Прегель в Кенигсберге (в том месте, где река разделяется на два рукава - Старый и Новый Прегель) и семи мостах, соединяющих остров с берегами. Задача состояла в том, чтобы выяснить, можно ли обойти все семь мостов по непрерывному маршруту, побывав на каждом только один раз и вернувшись в исходную точку. Эйлер заменил участки суши точками, а мосты - линиями. Полученную конфигурацию Эйлер назвал графом, точки - его вершинами, а линии - ребрами. Вершины он разделил на четные и нечетные в зависимости от того, четное или нечетное число ребер выходит из вершины. Эйлер показал, что все ребра графа можно обойти ровна по одному разу по непрерывному замкнутому маршруту, лишь если граф содержит только четные вершины. Так как граф в задаче о кенигсбергских мостах содержит только нечетные вершины, мосты невозможно обойти по непрерывному маршруту, побывав на каждом ровно по одному разу и вернувшись к началу маршрута. Предложенное Эйлером решение задачи о кенигсбергских мостах зависит только от взаимного расположения мостов. Оно положило формальное начало топологии как разделу математики. К.Гаусс (1777-1855) создал теорию узлов, которой позднее занимались И.Листинг (1808-1882), П. Тэйт (1831-1901) и Дж. Александер. В 1840 А. Мебиус (1790-1868) сформулировал так называемую проблему четырех красок, которую впоследствии исследовали О. де Морган (1806-1871) и А. Кэли (1821-1895). Первым систематическим трудом по топологии были Предварительные исследования по топологии Листинга (1874). Основателями современной топологии являются Г. Кантор (1845-1918), А. Пуанкаре (1854-1912) и Л. Брауэр (1881-1966).
Разделы топологии. Топологию можно подразделить на три области: 1) комбинаторную топологию, изучающую геометрические формы посредством их разбиения на простейшие фигуры, регулярным образом примыкающие друг к другу; 2) алгебраическую топологию, занимающуюся изучением алгебраических структур, связанных с топологическими пространствами, с упором на теорию групп; 3) теоретико-множественную топологию, изучающую множества как скопления точек (в отличие от комбинаторных методов, представляющих объект как объединение более простых объектов) и описывающую множества в терминах таких топологических свойств, как открытость, замкнутость, связность и т.д. Разумеется, такое деление топологии на области в чем-то произвольно; многие топологи предпочитают выделять в ней другие разделы.
Некоторые основные понятия. Топологическое пространство состоит из множества точек S и набора S подмножеств множества S, удовлетворяющего следующим аксиомам: (1) все множество S и пустое множество принадлежат набору S; (2) объединение любой совокупности множеств из S есть множество из S; (3) пересечение любого конечного числа множеств из S есть множество из S. Множества, входящие в набор S, называются открытыми множествами, а сам этот набор - топологией в S.
См. МНОЖЕСТВ ТЕОРИЯ. Топологическое преобразование, или гомеоморфизм, одной геометрической фигуры S на другую, S', - это отображение (p (r) p') точек p из S в точки p' из S', удовлетворяющее следующим условиям: 1) устанавливаемое им соответствие между точками из S и S' взаимно однозначно, т.е. каждой точке p из S соответствует только одна точка p' из S' и в каждую точку p' отображается только одна точка p; 2) отображение взаимно непрерывно (непрерывно в обе стороны), т.е. если заданы две точки p, q из S и точка p движется так, что расстояние между ней и точкой q стремится к нулю, то расстояние между соответствующими точками p', q' из S' также стремится к нулю, и наоборот. Геометрические фигуры, переходящие одна в другую при топологических преобразованиях, называются гомеоморфными. Окружность и граница квадрата гомеоморфны, так как их можно перевести друг в друга топологическим преобразованием (т.е. изгибанием и растяжением без разрывов и склеиваний, например, растяжением границы квадрата на описанную вокруг него окружность). Сфера и поверхность куба также гомеоморфны. Чтобы доказать гомеоморфность фигур, достаточно указать соответствующее преобразование, но тот факт, что для каких-то фигур найти преобразование нам не удается, не доказывает, что эти фигуры не гомеоморфны. Здесь помогают топологические свойства.
Рис. 1. ПОВЕРХНОСТЬ КУБА И СФЕРА гомеоморфны, т.е. могут быть переведены друг в друга топологическим преобразованием, но ни поверхность куба, ни сфера не гомеоморфны тору (поверхности "бублика").
Топологическим свойством (или топологическим инвариантом) геометрических фигур называется свойство, которым вместе с данной фигурой обладает также любая фигура, в которую она переходит при топологическом преобразовании. Любое открытое связное множество, содержащее по крайней мере одну точку, называется областью. Область, в которой любую замкнутую простую (т.е. гомеоморфную окружности) кривую можно стянуть в точку, оставаясь все время в этой области, называется односвязной, а соответствующее свойство области - односвязностью. Если же некоторую замкнутую простую кривую этой области нельзя стянуть в точку, оставаясь все время в этой области, то область называется многосвязной, а соответствующее свойство области - многосвязностью. Представьте себе две круговые области, или диски, одну без дыр, а другую с дырами. Первая область односвязна, вторая многосвязна. Односвязность и многосвязность - топологические свойства. Область с дырой не может перейти при гомеоморфизме в область без дыр. Интересно отметить, что если в многосвязном диске провести по разрезу от каждой из дыр до края диска, то он станет односвязным. Максимальное число замкнутых простых непересекающихся кривых, по которым можно разрезать замкнутую поверхность, не разделяя ее на отдельные части, называется родом поверхности. Род - топологический инвариант поверхности. Можно доказать, что род сферы равен нулю, род тора (поверхности "бублика") - единице, род кренделя (тора с двумя дырками) - двум, род поверхности с p дырами равен p. Отсюда следует, что ни поверхность куба, ни сфера не гомеоморфны тору. Среди топологических инвариантов поверхности можно также отметить число сторон и число краев. Диск имеет 2 стороны, 1 край и род 0. Тор имеет 2 стороны, не имеет краев, а его род равен 1. Введенные выше понятия позволяют уточнить определение топологии: топологией называется раздел математики, изучающий свойства, которые сохраняются при гомеоморфизмах.
Важные проблемы и результаты. Теорема Жордана о замкнутой кривой. Если на поверхности проведена простая замкнутая кривая, то существует ли какое-либо свойство кривой, которое сохраняется при деформации поверхности? Существование такого свойства вытекает из следующей теоремы: простая замкнутая кривая на плоскости делит плоскость на две области, внутреннюю и внешнюю. Эта кажущаяся тривиальной теорема очевидна для кривых простого вида, например, для окружности; однако для сложных замкнутых ломаных дело обстоит иначе. Теорема была впервые сформулирована и доказана К.Жорданом (1838-1922); однако доказательство Жордана оказалось ошибочным. Удовлетворительное доказательство было предложено О.Вебленом (1880-1960) в 1905.
Теорема Брауэра о неподвижной точке. Пусть D - замкнутая область, состоящая из окружности и ее внутренности. Теорема Брауэра утверждает, что для любого непрерывного преобразования, переводящего каждую точку области D в точку этой же области, существует некоторая точка, которая остается неподвижной при этом преобразовании. (Преобразование не предполагается взаимно однозначным.) Теорема Брауэра о неподвижной точке представляет особый интерес потому, что она, по-видимому, является, наиболее часто используемой в других разделах математики топологической теоремой.
Проблема четырех красок. Проблема заключается в следующем: можно ли любую карту раскрасить в четыре цвета так, чтобы любые две страны, имеющие общую границу, были раскрашены в различные цвета? Проблема четырех красок топологическая, так как ни форма стран, ни конфигурация границ не имеют значения. Гипотеза о том, что четырех красок достаточно для соответствующей раскраски любой карты, была впервые высказана в 1852. Опыт показал, что четырех красок действительно достаточно, но строгого математического доказательства не удавалось получить на протяжении более ста лет. И только в 1976 К.Аппель и В. Хакен из Иллинойского университета, затратив более 1000 часов компьютерного времени, добились успеха.
Односторонние поверхности. Простейшей односторонней поверхностью является лист Мебиуса, названный так в честь А. Мебиуса, открывшего его необычайные топологические свойства в 1858. Пусть ABCD (рис. 2,а) - прямоугольная полоска бумаги. Если склеить точку A с точкой B, а точку C с точкой D (рис. 2,б), то получится кольцо с внутренней поверхностью, наружной поверхностью и двумя краями. Одну сторону кольца (рис. 2,б) можно окрасить. Окрашенная поверхность будет ограничена краями кольца. Жук может совершить "кругосветное путешествие" по кольцу, оставаясь либо на окрашенной, либо на неокрашенной поверхности. Но если полоску перед склеиванием концов перекрутить на полоборота и склеить точку A с точкой C, а B с D, то получится лист Мебиуса (рис. 2,в). У этой фигуры есть только одна поверхность и один край. Любая попытка окрасить только одну сторону листа Мебиуса обречена на неудачу, так как у листа Мебиуса всего одна сторона. Жук, ползущий по середине листа Мебиуса (не пересекая края), вернется в исходную точку в положении "вверх ногами". При разрезании листа Мебиуса по средней линии он не распадается на две части.
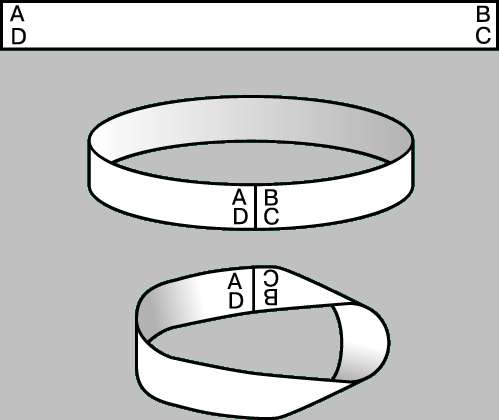
Рис. 2. СКЛЕЕННАЯ В КОЛЬЦО ПОЛОСКА (б) имеет внутреннюю и внешнюю стороны и два края. Лист Мебиуса (в), склеенный из перекрученной на полоборота прямоугольной полоски (а), имеет только одну сторону и один край.
Узлы. Узел можно представлять себе как запутанный кусок тонкой веревки с соединенными концами, расположенный в пространстве. Простейший пример - из куска веревки сделать петлю, пропустить один из ее концов сквозь петлю и соединить концы. В результате мы получим замкнутую кривую, которая остается топологически той же самой, как бы ее ни растягивать или скручивать, не разрывая и не склеивая при этом отдельные точки. Проблема классификации узлов по системе топологических инвариантов пока не решена.
ЛИТЕРАТУРА
Ху Сы-цзян. Теория гомотопий. М., 1964 Куратовский А. Топология, тт. 1-2. М., 1966, 1969 Спеньер Э. Алгебраическая топология. М., 1971 Александров П.С. Введение в теорию множеств и общую топологию. М., 1977 Келли Дж. Общая топология. М., 1981
Орфографический словарь
Словарь ударений
Формы слов для слова топология
тополо́гия, тополо́гии, тополо́гий, тополо́гиям, тополо́гию, тополо́гией, тополо́гиею, тополо́гиями, тополо́гиях
Синонимы к слову топология
Морфемно-орфографический словарь
Грамматический словарь
Словарь иностранных слов
Сканворды для слова топология
- Этот раздел математики утверждает, что бублик и кружка - одно и то же.
- Раздел математики.
- Эту науку часто называют геометрией на резиновом листе.
- Наука о свойствах геометрических фигур.
- Способ объединения компьютеров между собой в сети.