моск.

кольцо

Последняя остановка (станция) на линии городского общественного транспорта.

сущ., кол-во синонимов: 5

Составить слова из слова конечная

конечная генеральная совокупность - по существу, это всего лишь тот случай когда исследуется полностью один конкретный текст или тексты одного автора.

Составить слова из слова конечная генеральная совокупность

Коне́чная матема́тика (дискретная математика), раздел математики, занимающийся изучением свойств объектов конечного характера. К их числу могут быть отнесены, например, конечные группы, конечные графы, некоторые математические модели преобразователей информации.

* * *

КОНЕЧНАЯ МАТЕМАТИКА - КОНЕ́ЧНАЯ МАТЕМА́ТИКА (дискретная математика), раздел математики, занимающийся изучением свойств объектов конечного характера. К их числу могут быть отнесены, напр., конечные группы, конечные графы, некоторые математические модели преобразователей информации.

КОНЕЧНАЯ МАТЕМАТИКА (дискретная математика) - раздел математики, занимающийся изучением свойств объектов конечного характера. К их числу могут быть отнесены, напр., конечные группы, конечные графы, некоторые математические модели преобразователей информации.

Составить слова из слова конечная математика

част. разг.

1. Употребляется при выражении согласия, утверждения, соответствуя по значению сл.: да, разумеется.

2. Употребляется как вводное слово, соответствующее по значению сл.: без сомнения, само собою разумеется.

КОНЕ́ЧНО - служ., ???

1. Вы используете слово конечно, чтобы подчеркнуть уверенность в том, что вы говорите.

Она, конечно, доверяла мне. | Конечно, никто не знал о нашем договоре.

= разумеется, безусловно

2. Вы говорите конечно, когда соглашаетесь с тем, что только что сказал ваш собеседник.

Так он всё рассказал тебе? - Конечно. | - Он собирается извиниться перед нами? - Конечно, нет!

КОНЕ́ЧНО [шн].

1. вводное слово. Несомненно, само собою разумеется, естественно. Конечно, вы можете не согласиться.

2. утвердительная частица. Да, разумеется (разг.). - Можно мне закурить? - Конечно.

КОНЕ́ЧНО [шн ].

1. вводн. Само собой разумеется, без сомнения. Он, к., прав.

2. частица. Употр. при утверждении, подтверждении, да, разумеется. Вы любите музыкуЌ.!

3. Выражает сомнение, уверенность в обратном (разг. ирон.). Бросаю курить, последняя сигарета. К.! (т. е. очень сомневаюсь, не верю).

КОНЕ́ЧНО

I. частица. Употр. при выражении согласия, подтверждения сказанного; да, разумеется. Есть будешь? - К.! Вы говорите по-английски? - К.!

II. вводн. сл. Разумеется, несомненно. К., привычка много значит. Вы, к., к нам придёте?

1. вводн. сл.

Само собой разумеется, без сомнения.

[Маша:] Конечно, много значит привычка. Чехов, Три сестры.

Вам до меня, конечно, нет никакого дела. А. Н. Толстой, Сестры.

2. утвердительная частица. разг.

Да, разумеется.

- Вам здесь лучше, чем в прежнем флигельке? - спросил Павел Петрович вежливо, но без малейшей улыбки. - Конечно, лучше-с. Тургенев, Отцы и дети.

[Зобунова:] Средство это - дорогое! [Булычов:] Конечно! М. Горький, Егор Булычов и другие.

 (греч. τελευταῖον) наконец.

вводное слово и частица

1. Вводное слово. То же, что «несомненно, разумеется, действительно». Выделяется знаками препинания. Подробно о пунктуации при вводных словах см. в Приложении 2. (Приложение 2)

Сергей Петрович воспитания, конечно, не получил, по-французски не говорит; но он, воля ваша, приятный человек. И. Тургенев, Дворянское гнездо. Городок Биско, конечно, падал, но как бы то ни было, этот городок был почти что отечеством нашему герою… М. Пришвин, Серая сова. Стишки, конечно, дрянь, но с формальной точки зрения и они тоже поэзия. Б. Акунин, Внеклассное чтение.

2. Утвердительная частица (в ответной реплике). То же, что «да». Обособляется или оформляется как отдельное предложение.

«В Соловце будете останавливаться?» - cпросил горбоносый. «Конечно, - сказал я. - Я в Соловец и еду». А. и Б. Стругацкие, Понедельник начинается в субботу. «Конечно, да, - грустно отвечал он. - Но как я скучаю без него, если бы вы знали!» В. Каверин, Два капитана.

@ Не выделяется знаками препинания слово «конечно» в начале ответной реплики, произносимой тоном уверенности, убежденности: Конечно же это так! Конечно правда!

коне́чно, вводн. сл. и частица

коне́чно [шн]

коне́чно. Произносится [коне́шно] и допустимо [коне́чно].

конечно

нареч, кол-во синонимов: 82

(само собой) разумеется, несомненно, безусловно, бесспорно, обязательно, естественно, заведомо, без (или вне) (всякого) сомнения, не подлежит сомнению, не иначе, иначе и быть не может, двух мнений быть не может, нечего и говорить, явно; наверняка, что и говорить, спору нет, известное (или ясное) дело, факт, понятно, натурально, не иначе (разг.); как пить дать, известно, без вопросов (прост.); всеконечно (устар.); знамо, вестимо (устар. прост.)

/ как ответ: ещё бы(!), а (то) как же(!), что за вопрос(!), спрашиваешь(!), а то нет(!) (разг.)

/ о будущем: будьте благонадёжны (устар. разг.); попомни(те) мои слова, помяните) мои слова (разг.)

/ о прошлом: как и следовало ожидать

см. также да, действительно

неизм.

1.

да

ну да

ну конечно

безусловно

несомненно

ага

разумеется

ну разумеется

само собой разумеется

(сообщение утверждения, согласия))

2.

разумеется

само собой разумеется

безусловно

бесспорно

несомненно

без сомнения

вне сомнения

естественно

само собой

натурально

понятно

известно

понятное дело

знамо

знамо дело

вестимо

без всякого сомнения

известное дело

КОНЕЧНО

КОНЕЧНО, безоговорочно, безусловно, бесспорно, естественно, заведомо, несомненно, положительно, разумеется, явно, устар. вестимо, устар. всеконечно, устар. знамо, разг. наверняка, разг. понятно, разг.-сниж. известно, разг.-сниж. натурально, разг.-сниж. обязательно, разг.-сниж. факт

Разумеется, само собой разумеется, несомненно, очевидно, понятно, вестимо, ясно, ясное дело, нечего говорить, что и говорить, спору нет, все конечно.

Ср. . ..

См. да, действительно...

▲ да

↑ определенно

конечно - определенно "да".

ну конечно.

несомненно.

без [вне] сомнения [ - ья]. нет сомнений.

не подлежит сомнению. кто в этом сомневается.

бесспорно.

безусловно.

я думаю!

держу пари, что...

заведомо (# известно).

как пить дать.

он еще спрашивает.

а то как же. а то! (в футбол играешь? - #). а то нет.

как же ? ну а как же.

прост: знамо . известное дело. вестимо. видимое дело.

понятное дело. понятная вещь.

естественно (#, он согласился). естественное дело.

прост: натурально. в натуре.

еще бы! (# ты был недоволен!).

сам понимаешь.

смело (за столом # поместятся пять человек).

тем более. подавно

слов [слова] нет. что за вопрос! вопроса нет.

не говори. что за разговор!

о чем разговор [речь]!

не говоря о чем.

и говорить нечего. нечего и говорить.

что и [там] говорить. что об этом говорить.

кто говорит.

и никак иначе. так и только так. не иначе как.

что - что, а... (# это мы умеем делать).

мудрено ли. не мудрено.

прост: будь уверен. будь спок.

как штык.

см. истинно, с, несомненность, понятный

коне́чно.

коне́чно вводн.; част.

Это вводное слово образовано от прилагательного, произведенного от конец.

Восходит к прилаг. ср. р. ед. ч., образованному от *копъкъ- "конец". *Копъкъ является производным от основы коп->кон-.

Искон. Суф. производное от конец. Исходно - «окончательно», далее - «несомненно». Ср. аналогичные натурально < нем. natürlich «конечно» < «по натуре» - производное от Natur «природа» (< лат. natura «природа, вселенная» < «нарожденное» - от nascor «рождаюсь, происхожу, возникаю», ср. кон).

Составить слова из слова конечно

коне/чно-вы/грузочный

Составить слова из слова конечно-выгрузочный

коне/чно-моде/льный

Составить слова из слова конечно-модельный

коне́чно-море́нный

Составить слова из слова конечно-моренный

коне́чно-ра́зностный

Составить слова из слова конечно-разностный

Прост. Непременно, обязательно; конечно.

- Корнеич передёрнул усами… Наконец осторожно возразил: - Я, конечное дело, передам Михаилу Михайлычу. Только это, товарищ начальник, лодырь (Б. Можаев. Живой).

- Я бы и дом командира батареи тушить, конечное дело, прибежал бы, да я стоял тем часом на посту (Л. Борисов. Потревоженные тени).

Волог., Кар. То же, что известное дело. СВГ 3, 97; СРГК 1, 446.

Составить слова из слова конечное дело

конечнозна/чный

Составить слова из слова конечнозначный

конечноме/рный

Составить слова из слова конечномерный

конечносвя/зный

Составить слова из слова конечносвязный

мн.

Руки, ноги у человека, у животных - органы движения.

КОНЕ́ЧНОСТИ, -ей, мн (ед коне́чность, -и, ж).

Руки и ноги у человека, органы движения у животных (ноги, лапы).

По стене к башне шла стертая, выветрившаяся, еле заметная лестница. По-обезьяньи, на четырех конечностях, я пересек освещенную часть стены… (В. Акс.).

КОНЕ́ЧНОСТИ -ей; мн. (ед. коне́чность, -и; ж.). Руки, ноги у человека; у животных - органы движения. Верхние, нижние к. (у человека). Передние, задние к. (у животных). Дрожь в конечностях от усталости.

* * *

коне́чности - 1) у животных органы, служащие главным образом для передвижения. Простейшие конечности - параподии некоторых кольчатых червей. Парные конечности рыб - плавники. У птиц и летучих мышей передние конечности превратились в крылья, у китообразных - в ласты. Скелет конечностей состоит из хрящей или (чаще) костей, соединённых друг с другом и приводимых в движение мышцами.

2) У человека верхние конечности - руки, нижние конечности - ноги.

* * *

КОНЕЧНОСТИ - КОНЕ́ЧНОСТИ,

1) у животных органы, служащие главным образом для передвижения. Простейшие конечности - параподии (см. ПАРАПОДИИ) некоторых кольчатых червей. Парные конечности рыб - плавники. У птиц и летучих мышей передние конечности превратились в крылья, у китообразных - в ласты. Скелет конечностей состоит из хрящей или (чаще) костей, соединенных друг с другом и приводимых в движение мышцами.

2) У человека верхние конечности - руки, нижние конечности - ноги.

КОНЕЧНОСТИ -1) у животных органы, служащие главным образом для передвижения. Простейшие конечности - параподии некоторых кольчатых червей. Парные конечности рыб - плавники. У птиц и летучих мышей передние конечности превратились в крылья, у китообразных - в ласты. Скелет конечностей состоит из хрящей или (чаще) костей, соединенных друг с другом и приводимых в движение мышцами.2) У человека верхние конечности - руки, нижние конечности - ноги.

-ей, мн. (ед. коне́чность, -и, ж.).

Руки, ноги у человека, у животных - органы движения.

Верхние конечности. Нижние конечности. Задние конечности.

коне́чности, -ей, ед. ч. -ость, -и

коне́чности, коне́чностей, коне́чностям, коне́чностями, коне́чностях

сущ., кол-во синонимов: 5

члены, руки и ноги; руки-ноги (разг.)

руки-ноги, обрезки, члены, руки и ноги, дрова

КОНЕЧНОСТИ

КОНЕЧНОСТИ, члены, разг. руки-ноги, разг.-сниж. лапы, жарг. ветки, жарг. пакли

▲ орган (животных)

↑ передвижение

конечность - орган движения животных.

нога. лапа. клешня. ласт.

коготь. копыто.

ногти - плоские роговые образования на тыльной стороне концевых фаланг пальцев

у приматов.

плавники - органы движения водных животных.

крыло. надкрылья.

щупальца - подвижные выросты тела у многих беспозвоночных.

жгутики.

↓ двигать конечностями, хватать

▼ рука, нога

см. являться (чем), исполнитель, СИСТЕМАТИКА ЖИВОТНЫХ

коне́чности мн. от ж 8a

Составить слова из слова конечности

I ж.

отвлеч. сущ. по прил. конечный

II ж.

см. конечности

КОНЕ́ЧНОСТЬ, конечности, жен.

1. Рука, нога или другой обособленный орган движения у животных (анат.). Снабженные копытами конечности. Ампутация конечностей. Передние, задние конечности.

2. только ед. отвлеч. сущ. к конечный в 1 знач.; ант. бесконечность (книжн., редк.). Коенчность жизни.

КОНЕ́ЧНОСТЬ, -и, жен.

1. см. конечный.

2. Рука, нога, а также, у животных, отдельный орган движения. Верхние, нижние конечности (у человека). Передние, задние конечности (у животных).

КОНЕ́ЧНОСТЬ см. Коне́чный.

-и, ж.

Свойство по прил. конечный (в 1 знач.).

Даже в счастливые минуты творчества ему не были противны мысли о смерти, разрушении и конечности. Чехов, Жена.

КОНЕЧНОСТЬ -

характер того, что имеет конец. Этот термин, чрезвычайно распространенный в современной философии, обозначает прежде всего характер, присущий человеческому сознанию, раскрывающийся в тоске, связанной со смертью (Хайдеггер), в невозможности для личности выразить себя, заявить о себе раз и навсегда в слове или действии, наконец, в невозможности сделать все в жизни одновременно и в необходимости свободного и произвольного выбора между предлагаемыми нам возможностями (Сартр).

Пятая конечность. Жарг. мол. Шутл. Ягодицы. Максимов, 194.

Трясти конечностями. 1. Жарг. шк. Шутл. Поднимать руку на уроке. 2. Жарг. мол. Шутл. Танцевать. Максимов, 194.

коне́чность, -и (свойство)

коне́чность, коне́чности, коне́чностей, коне́чностям, коне́чностью, коне́чностями, коне́чностях

сущ., кол-во синонимов: 10

член, рука, педипальпы, лапа, культя, палец, масёл, культяпка, нога

бесконечность

вечность

коне́ч/н/ость/.

коне́чность ж 8a

- И рука, и нога, и лапа, и копыто.

- Отдельный орган движения животных, человека.

Составить слова из слова конечность

конечность (лингвостилистической) подсистемы - определяется наличием или возможностью составить или получить прежде всего конечный по числу лингвистических единиц словарь-лексикон этой подсистемы. Здесь, естественно, подразумевается относительная конечность подсистем, ибо даже весь живой естественный язык не обладает абсолютной закрытостью и, следовательно, конечностью составляющих его лексических единиц. Такой закрытостью может обладать только мертвый естественный язык, например, готский, аккадский, арамейский, латинский и др., но и здесь закрытость латинского все же относительна, т.к. мертвый латинский язык пополняется новыми терминами, обслуживающими новые понятия науки и техники времени.

Составить слова из слова конечность (лингвостилистической) подсистемы

Исчисление конечных разностей связано с изучением свойств и применений разностей между соседними членами какой-нибудь последовательности или между значениями функции в точках, расположенных с постоянным интервалом в некотором пространстве. Слово "конечные" используется здесь в несколько устаревшем смысле "не бесконечно малые", т.е. не связанные с предельными переходами. Поскольку дифференциальное исчисление занимается изучением пределов разностей, а исчисление конечных разностей - самими разностями, то естественно, что между этими двумя теориями существуют много параллелей. Исчисления конечных разностей используются при интерполяции в математических таблицах, при суммировании числовых рядов, при вычислении интегралов и дифференцировании функций. Разности встречаются также в любой ситуации, когда надо описать поведение объекта, который испытывает воздействие меняющихся условий на определенном расстоянии (во времени и в пространстве). Например, термостату требуется значительное время, чтобы отреагировать на изменение температуры, поэтому он реагирует не на текущую температуру, а на ту, что была минуту назад. Другой пример: автомашиной управляет водитель, которому требуется какое-то время, чтобы отреагировать на возникшую на дороге ситуацию. Под конечной разностью первого порядка функции f (x) принято понимать величину

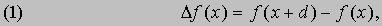
где d - некоторая постоянная, которую часто, но не всегда, принимают равной 1. Разность второго порядка обозначается D2f и представляет собой разность разностей, т.е.

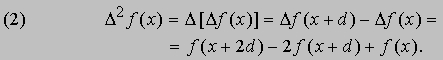
Продолжив этот процесс, мы получим разности более высоких порядков D3f (x), D4f (x), ј . Данные выше определения можно также применить к членам любых последовательностей величин, например, к последовательности 3, 6, 11, 18, 27, 38, ј.

Первые разности равны 6 - 3, 11 - 6, 18 - 11, 27 - 18, 38 - 27, ј, т.е. 3, 5, 7, 9, 11, ј; разности второго порядка постоянны и равны 2. В общем виде такие последовательности можно записать как

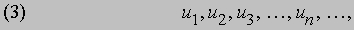
где разности первого, второго и т.д. порядков определяются выражениями

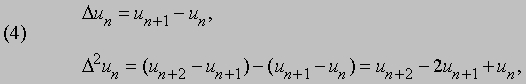
а n может принимать любое допустимое для индекса значение. В некоторых приложениях используются последовательности вида

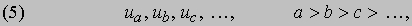
где индексы могут принимать любые убывающие значения. В этом случае вместо символа D используется символ

разделенной разности.

Разделенные разности первого и второго порядков определяются следующим образом:

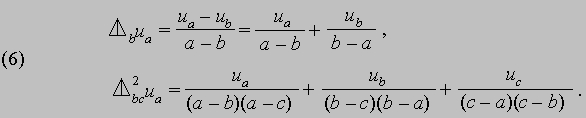
Помимо уже названных выше приложений, исчисление конечных разностей используется в страховании, теории вероятностей и статистике. В последние годы с изобретением быстродействующих компьютеров конечные разности стали все более широко применяться при решении дифференциальных уравнений, обыкновенных и в частных производных, многие из которых ранее было невозможно решить другими математическими методами.

У истоков теории. Хотя исследование свойств и использование конечных разностей приходится на современный период развития математики, Птолемей (ок. 150 н.э.) ввел в Альмагесте таблицу разностей первого порядка, чтобы облегчить расчеты в таблице длин хорд. Разности второго порядка использовал при вычислении своих таблиц логарифмов в 1624 Г. Бриггс. Теория интерполяции берет начало со знаменитой пятой леммы из 3-й книги Математических начал (1687) И. Ньютона, в которой впервые была приведена формула, носящая ныне его имя. Частный случай формулы Ньютона, открытый также независимо его современником Дж. Грегори (1638-1675), приведен ниже (см. формулу (7)). В общей формуле интерполяции Ньютона использовались разделенные разности, хотя этот термин, по-видимому, был введен О.де Морганом (1806-1871) в 1848. Первое применение исчисления конечных разностей к задачам теории вероятностей принято связывать с именами П.де Монтмора (1678-1719) и А. де Муавра (1667-1754). Хотя Л. Эйлер (1707-1783) в своих работах по дифференциальному исчислению использовал предельные переходы в конечных разностях, основания современной теории конечных разностей были заложены в основном Ж.Лагранжем (1736-1813) и П. Лапласом (1749-1827). Первый из них ввел в исчисление конечных разностей символические методы, второй сделал конечные разности главным инструментом в своей Аналитической теории вероятностей (1812). Под влиянием этих работ математики 19 в. принялись интенсивно разрабатывать предмет, и в 1860 Дж. Буль выпустил свой классический Трактат об исчислении конечных разностей. С тех пор это исчисление и круг его приложений существенно расширились. Одно из наиболее важных приложений конечные разности нашли в статистике. Особенно полезными они оказались в теории сериальной корреляции, в анализе случайных последовательностей и статистических временных рядов.

Интерполяция. Чтобы понять, как конечные разности используются при интерполяции, рассмотрим следующую таблицу:

Величины в первом столбце таблицы называются значениями аргумента, во втором - табличными значениями функции. В трех следующих столбцах приведены разности первого, второго и третьего порядков. Числа 7, 12, 6 называются "ведущими" или "диагональными разностями", соответствующими первому аргументу. Термин "диагональные" использован потому, что разности относительно соответствующих аргументов и табличных значений располагаются не по горизонтали. Величина (1/2) (19 + 37) = 28 называется центральной разностью, соответствующей третьему аргументу, и обозначается символом md. Греческая буква m означает среднее, md - среднее соседних разностей. Величина 18 называется центральной разностью второго порядка и обозначается символом d2 . Термин "центральная" указывает на то, что эти разности расположены по центру относительно аргумента, т.к. они либо лежат на одной горизонтали с аргументом, либо являются средними значений, расположенных по соседству с этой горизонталью. Обобщая, таблицу величин можно записать в символических обозначениях следующим образом:

Величины D f (x), D2 f (x), D3 f (x) представляют собой диагональные разности, соответствующие аргументу x. Если мы захотим найти табличные значения для аргумента x + pd, где p - некоторое произвольно выбранное число, то необходимо подставить соответствующие значения в следующий ряд, известный под названием интерполяционной формулы Грегори - Ньютона (в русскоязычной литературе эту формулу принято называть формулой Ньютона):

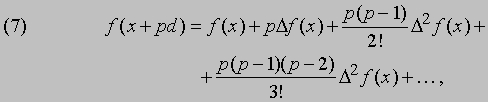
где 2! (читается "два факториал") означает 1*2, 3! = 1*2* 3 и т.д. В литературе встречается несколько вариантов формулы Грегори - Ньютона. В некоторых из них вместо диагональных разностей используются центральные разности. Так, центральные разности, соответствующие аргументу x, определяются следующим образом:

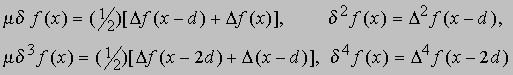
и т.д. В качестве примера найдем по формуле интерполяции значение (2,5)3 из приведенной выше числовой таблицы. Так как d = 1, p = 1/2 и диагональные разности, соответствующие x = 2, равны D = 19, D2 = 18, D3 = 6, находим по формуле интерполяции

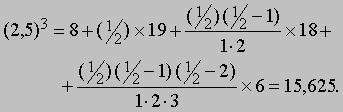
Символические методы. Один из наиболее удивительных аспектов исчисления конечных разностей связан с символическими (или операторными) методами. Чтобы понять их суть, рассмотрим символ E, называемый оператором и определяемый соотношением

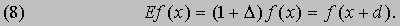
Пусть E 2f (x) - результат действия E на Ef (x), тогда E 2f (x) = f (x + 2d). Пользуясь математической индукцией, получаем для произвольного индекса p формулу

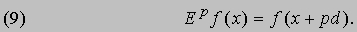
Опустим в формуле (8) символ функции и рассмотрим соотношение между одними лишь символами E = 1 + D. Оказалось, что с этим равенством и с другими, выводимыми из него, можно обращаться в соответствии с обычными правилами алгебры. Если степени символов интерпретировать как результат последовательного применения операторов Е и D, то полученные формулы также будут справедливы. Рассмотрим, например, Ep = (1 + D)p. Если правую часть равенства разложить по формуле бинома, а полученный ряд применить к f (x), мы получим разложение, стоящее в правой части интерполяционной формулы (7). Из (9) следует, что запись Epf (x) эквивалентна f (x + pd). Таким образом, биномиальное разложение, примененное к f (x) как операторное и приравненное к f (x + pd), дает формулу Грегори - Ньютона. Этот пример иллюстрирует характерные особенности символического (операторного) метода. Он позволил открыть так много замечательных формул, что большинство авторов, впервые его применивших, в своих работах не могли не выразить своего восхищения его мощью. Тайна эффективности этого метода кроется в том, что основной закон комбинирования алгебраических величин, с одной стороны, и операторы, такие, как D и Е, с другой, удовлетворяют правилу сложения показателей степеней

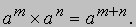
Следует иметь в виду, однако, что в первом случае символ произведения интерпретируется как обычное умножение, а во втором как последовательное выполнение операций. Символические методы позволяют установить связь исчисления конечных разностей с дифференциальным исчислением. Чтобы убедиться в этом, обозначим производную от f (x) символом Df (x), вторую производную - символом D 2f (x) и т.д. Разложение f (x + d) в ряд Тейлора (см. МАТЕМАТИЧЕСКИЙ АНАЛИЗ) можно записать символически в виде

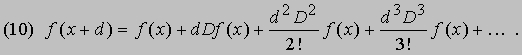
Учитывая, что разложение в ряд функции ez, где e = 2,71828ј - основание натуральных логарифмов, имеет вид

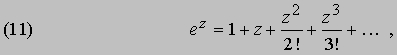
разложение (10) можно записать как

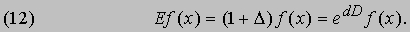
Опуская, как и прежде, символ функции, получаем чисто символическое уравнение

Если разрешить его относительно D по обычным правилам алгебры и принять во внимание разложение в ряд Тейлора для логарифмической функции, то получим

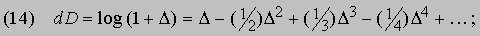
т.е.

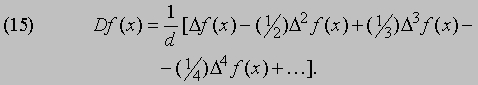
Еще более замечательные соотношения получаются для обратных операторов D-1 и D-1. Первый оператор интерпретируется как символ интегрирования т, а второй - как символ суммирования е, определяемый следующим образом:

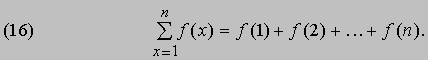
Хотя D-1 и D-1 следует рассматривать как символы операторов, примечательно, что над ними можно производить алгебраические операции так, как если бы это были величины 1/D и 1/D. В качестве примера применения символического метода решим уравнение (13) относительно 1/D:

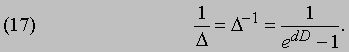
Для интерпретации этого соотношения необходимо иметь в виду разложение

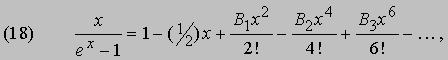
где B1 = 1/6, B2 = 1/30, B3 = 1/42 - т.н. числа Бернулли, названные так в честь открывшего их Я.Бернулли (1654-1705). Эти числа используются в различных разделах исчисления конечных разностей. Бернулли с гордостью заявлял, что с их помощью он нашел сумму десятых степеней первой тысячи натуральных чисел "за половину четверти часа". Подставив x вместо dD в правой части разложения (18) и сделав небольшие преобразования, можно записать (17) в виде

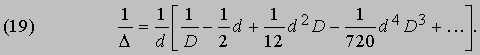
Вспомнив, что означали эти символы, и применив формулу к f (x), получим следующее разложение:

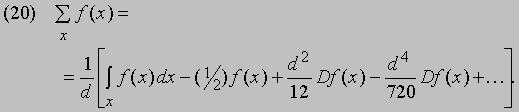
Суммирование рядов. Метод конечных разностей особенно удобен при суммировании рядов. Чтобы убедиться в этом, предположим, что в (1) d = 1, и рассмотрим сумму

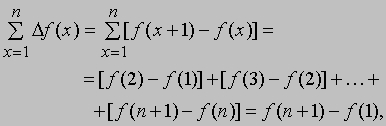
которую можно записать в более компактном виде

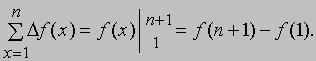
Заметим, что

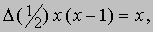
откуда

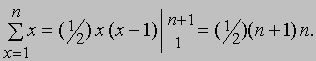
Тот же результат можно получить и из формулы (20). В этом случае, полагая d = 1 и f (x) = x, получаем

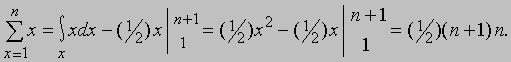
Разностные уравнения. В некоторых приложениях метода конечных разностей встречаются уравнения, типичными примерами которых являются следующие:

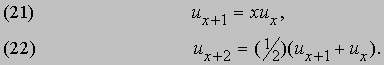
Такие уравнения называются "разностными уравнениями", так как их можно превратить в соотношения между разностями u. Например, первое уравнение можно записать в виде Dux = (x - 1)ux, а второе - в виде D2ux + 3/2 Dux = 0. Первое называется разностным уравнением первого порядка, второе - второго порядка. Такие уравнения встречаются, в частности, в приложениях теории вероятностей, для нахождения последовательных значений величины ux, когда x пробегает некоторую последовательность целых чисел. Такие образом, для уравнения (21), если u1 =1 и x = 2, 3, 4, ј, n, получаем

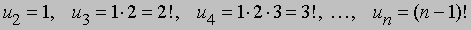
Аналогично, для (22), если u0 = 1, u1 = 0 и x = 2, 3, 4, ј, n, мы получаем следующую последовательность значений:

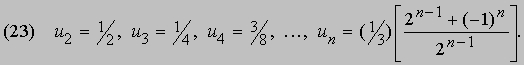
В общем случае разностные уравнения имеют также решения, определяемые в непрерывной области значений x. Например, частным решением уравнения (21) является "гамма-функция" G (x), так как одно из фундаментальных свойств этой функции состоит в том, что G (x + 1) = xG (x) (см. ФУНКЦИЯ). Такое решение мы получим из уравнения (22), положив ux = mx. Подставляя эту функцию в (22), мы получаем уравнение

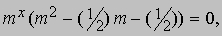
откуда m = 1, m = -1/2. Следовательно, уравнение (22) имеет решение

где А и В - произвольные постоянные. В частности, для A = 1/3 и B = 2/3 мы получим при целочисленных значениях x последовательность (23). Но (24) - не самое общее решение уравнения (22), так как другое решение можно получить, умножив любое частное решение на g (x), где g (x) - произвольная функция единичного периода, т.е. удовлетворяет уравнению

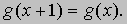
Примерами таких функций могут служить sin2px, cos2px, sin6px, cos6px и т.д. Подставляя в (22)

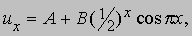
нетрудно убедиться в том, что ux - решение уравнения (22). Это решение получено при умножении второго члена в правой части (24) на подходящим образом выбранную функцию единичного периода.

Составить слова из слова конечные разности

прил.

1. Имеющий конец в пространстве, во времени.

Ant:

бесконечный

2. Находящийся на конце, в конце чего-либо, последний в определённом ряду предметов или явлений.

3. Являющийся осуществлением чего-либо, завершением, результатом какого-либо процесса, цикла и т.п.

КОНЕ́ЧНЫЙ - прил., употр. сравн. часто

1. Если что-либо конечно, значит, оно имеет конец во времени и пространстве.

Материя конечна. | Человек конечен.

2. Конечным называют то, что находится в конце.

Конечная остановка. | Он назвал конечный пункт перелёта.

3. Результат, итог и т. п. называют конечным, если вы получили его после завершения какой-либо работы, какого-либо процесса.

Конечный итог его операций будет вполне удовлетворительным. | Нас прежде всего интересует конечный продукт. | Наши конечные цели не вполне совпадают.

4. Вы используете выражение в конечном счёте или в конечном итоге, когда хотите подчеркнуть окончательный результат, итог чего-либо.

В конечном итоге жизнь развела их в разные стороны. | Партия «зелёных», в конечном счёте, привлекает внимание общественности к экологическим проблемам.

= в конце концов

коне́чность сущ., ж.

Конечность бытия, рекурсии.

КОНЕ́ЧНЫЙ, конечная, конечное.

1. Имеющий конец; ант. бесконечный (книжн.). Человек - существо конечное.

2. Находящийся на конце чего-нибудь. Конечный дом на этой улице. Конечные буквы алфавита. Конечная станция железной дороги.

3. Последний, предельный, являющийся осуществлением какого-нибудь идеала, цели (книжн.). Конечная цель. «Пушкин - это русский человек в конечном его развитии.» Гоголь.

|| Лежащий в основе чего-нибудь, определяющий собой что-нибудь (книжн.). Конечная причина.

• В конечном счете (книжн.) - в последнем итоге. Конечная величина (мат.) - величина, изменяющаяся в определенных пределах, не равная ни нулю ни бесконечности.

КОНЕ́ЧНЫЙ, -ая, -ое; -чен, -чна.

1. см. конец.

2. Имеющий конец (во времени), не бесконечный (высок.). Жизнь человека конечна.

3. полн. Основной, являющийся пределом чего-н., самый главный. Конечная цель.

4. полн. Заключающий собой какой-н. процесс, являющийся результатом работы, обработки. К. результат. К. продукт.

В конечном счёте в конце концов, в итоге.

| сущ. конечность, -и, жен. (ко 2 знач.).

КОНЕ́ЧНЫЙ -ая, -ое; -чен, -чна, -чно.

1. Имеющий конец (1 зн.), предел (в пространстве, во времени; противоп.: бесконе́чный). Жизнь человека конечна.

2. только полн. Находящийся на конце или в конце чего-л.; последний. К. пункт путешествия. К-ая остановка. К. абзац. К-ое четверостишие.

3. только полн. Являющийся завершением какого-л. процесса, цикла и т.п. К. результат. К. продукт производства. К-ая цель. Уверенность в конечной победе над врагом.

◁ В коне́чном счёте; в коне́чном итоге, в зн. нареч. В окончательном итоге, в конце концов. В конечном счёте он оказался прав. Коне́чность, -и; ж. (1 зн.).

1) коне́чный

-ая, -ое; -чен, -чна, -чно.

1. Имеющий конец, предел (в пространстве, во времени); противоп. бесконечный.

Период этот будет конечен, а время бесконечно. Л. Толстой, Война и мир.

2. только полн. ф.

Находящийся на конце или в конце чего-л.; последний.

Помнится, прочтя однажды «Анчар», он [Мериме] после конечного четверостишия заметил: «Всякий новейший поэт не удержался бы тут от комментариев». Тургенев, .

Пароход приближался к конечному пункту рейса. Марков, Строговы.

3. только полн. ф.

Являющийся завершением какого-л. процесса, цикла и т. д.

Конечный результат.

◊

Самым ценным материалом является конечный продукт производства - чугун. М. Павлов, Воспоминания металлурга.

Конечная цель всего нашего мышления --- состоит в том, чтобы разрешить навсегда неизбежный вопрос о голодных и раздетых людях. Писарев, Реалисты.

В лейтенанте жила безраздельная уверенность в конечной победе над любым врагом. Казакевич, Весна на Одере.

◊

в конечном счете{ (или итоге)}

в окончательном итоге, в конце концов.

2) …коне́чный

-ая, -ое.

Вторая составная часть сложных слов, обозначающая:

1) имеющий столько концов, сколько указано в первой части, например: пятиконечный, шестиконечный;

2) имеющий такой конец, какой указан в первой части, например: остроконечный, тупоконечный.

 (греч. τέλειος) совершенный, окончательный.

коне́чный; кратк. форма -чен, -чна

коне́чный, -чен, -чна, -чно, -чны

коне́чный, коне́чная, коне́чное, коне́чные, коне́чного, коне́чной, коне́чных, коне́чному, коне́чным, коне́чную, коне́чною, коне́чными, коне́чном, коне́чен, коне́чна, коне́чно, коне́чны, коне́чнее, поконе́чнее, коне́чней, поконе́чней

прил., кол-во синонимов: 23

1. последний, концевой

2. см. окончательный

прил.

последний

концевой

конец

См. окончательный, последний...

Syn: завершающий, завершенный, заключительный, концевой, крайний, последний, окончательный, финитный

Ant: начальный, открывающий, первый

бесконечный

См. finale 2.

коне́ч/н/ый.

коне́чный п 1*a

КОНЕЦКИЙ КОНЕЧНЫЙ КОНЧАНСКИЙ КРАЙНЕВ КРАЙНОВ КОНЦЕВОЙ КОНЦЕВЕНКО КРАЙНЯК НАКОНЕЧНЫЙ

Так иногда называли людей, живущих в конце деревни, то есть на самом ее краю. Прозвище превращалось в фамилию. Крайний, крайней - человек, живущий на краю деревни. (Ф) Конечный (195 чел.- Шенк. у.; там же в 1655 г. с этой фамилией несколько крестьян упомянуты в порядных записях). Термин конец с территориально-административным значением принесен на Север еще новгородцами. (Ф)

Составить слова из слова конечный

▲ ограниченный

↑ величина

<-> беспрерывный

конечность - ограниченность величины.

конечный (# время). финитный.

обозримость. обозримый (# время).

конечная линия - отрезок или замкнутая линия.

↓ временный, самый, РАЗМЕР, ВРЕМЯ

Составить слова из слова конечный (размер)

Коне́чный выключа́тель - то же, что концевой выключатель.

* * *

КОНЕЧНЫЙ ВЫКЛЮЧАТЕЛЬ - КОНЕ́ЧНЫЙ ВЫКЛЮЧА́ТЕЛЬ, то же, что концевой выключатель (см. КОНЦЕВОЙ ВЫКЛЮЧАТЕЛЬ).

КОНЕЧНЫЙ выключатель - то же, что концевой выключатель.

Составить слова из слова конечный выключатель

КОНЕ́ЧНЫЙ КОНТРО́ЛЬ.

См. контроль.

Составить слова из слова конечный контроль

♠ головной мозг

конечный мозг, шляпка мозга.

♥ большие полушария.

кора больших полушарий, неокортекс.

левое полушарие мозга, правое полушарие мозга

мозолистое тело.

подкорковый, субкортикальный.

↓ ходьба.

моделирование. предвидение.

кортикализация функций.

Составить слова из слова конечный мозг

предельный срок

Syn: предельный срок

Составить слова из слова конечный срок

Сиб. Конечно, разумеется. ФСС, 58.

Составить слова из слова конечным делом

Коне́чных прираще́ний фо́рмула (формула Лагранжа), формула дифференциального исчисления; даёт связь между приращением функции f(х) и значениями её производной:

f(b) - f(а) = (b-а)f΄(с), где а

КОНЕЧНЫХ ПРИРАЩЕНИЙ формула (формула Лагранжа) - формула дифференциального исчисления; дает связь между приращением функции f(х) и значениями ее производной: f(b??f(a)=(b?a)f (c), где a"c"b.

Составить слова из слова конечных приращений формула

Коне́чных ра́зностей исчисле́ние - раздел математики, в котором изучаются функции при дискретном (прерывном) изменении аргумента, в отличие от дифференциального исчисления и интегрального исчисления, где аргумент предполагается непрерывно изменяющимся.

* * *

КОНЕЧНЫХ РАЗНОСТЕЙ ИСЧИСЛЕНИЕ - КОНЕ́ЧНЫХ РА́ЗНОСТЕЙ ИСЧИСЛЕ́НИЕ, раздел математики, в котором изучаются функции при дискретном (прерывном) изменении аргумента, в отличие от дифференциального исчисления (см. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ) и интегрального исчисления (см. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ), где аргумент предполагается непрерывно изменяющимся.

КОНЕЧНЫХ РАЗНОСТЕЙ ИСЧИСЛЕНИЕ - раздел математики, в котором изучаются функции при дискретном (прерывном) изменении аргумента, в отличие от дифференциального исчисления и интегрального исчисления, где аргумент предполагается непрерывно изменяющимся.

Составить слова из слова конечных разностей исчисление