НЕЁ. род. и вин. от она в положении после предлогов. От нее. В нее.
неевклидова геометрия
Энциклопедия Кольера
НЕЕВКЛИДОВА ГЕОМЕТРИЯ - геометрия, сходная с геометрией Евклида в том, что в ней определено движение фигур, но отличающаяся от евклидовой геометрии тем, что один из пяти ее постулатов (второй или пятый) заменен его отрицанием. Отрицание одного из евклидовых постулатов (1825) явилось значительным событием в истории мысли, ибо послужило первым шагом на пути к теории относительности. Второй постулат Евклида утверждает, что любой отрезок прямой можно неограниченно продолжить. Евклид, по-видимому, считал, что этот постулат содержит в себе и утверждение, что прямая имеет бесконечную длину. Однако в "эллиптической" геометрии любая прямая конечна и, подобно окружности, замкнута. Пятый постулат утверждает, что если прямая пересекает две данные прямые так, что два внутренних угла по одну сторону от нее в сумме меньше двух прямых углов, то эти две прямые, если продолжить их неограниченно, пересекутся с той стороны, где сумма этих углов меньше суммы двух прямых. Но в "гиперболической" геометрии может существовать прямая CB (рис. 1), перпендикулярная в точке С к заданной прямой r и пересекающая другую прямую s под острым углом в точке B, но, тем не менее бесконечные прямые r и s никогда не пересекутся.
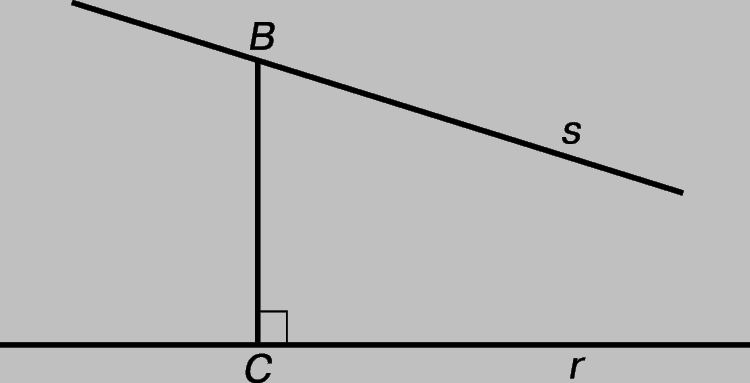
Рис. 1. В ГИПЕРБОЛИЧЕСКОЙ ГЕОМЕТРИИ может существовать прямая CB, перпендикулярная данной прямой r и пересекающая другую данную прямую s под острым углом в точке B так, что бесконечный луч s не пересекает прямую r.
Из этих пересмотренных постулатов следовало, что сумма углов треугольника, равная 180° в евклидовой геометрии, больше 180° в эллиптической геометрии и меньше 180° в гиперболической геометрии.
История. Первым неевклидовым геометром, вероятно, можно считать самого Евклида.
Его нежелание использовать "несамоочевидный" пятый постулат следует хотя бы из того, что свои первые двадцать восемь предложений Евклид доказывает, не прибегая к этому постулату. С первого века до н.э. до 1820 математики пытались вывести пятый постулат из остальных, но преуспели лишь в замене его различными эквивалентными допущениями, такими, как "две параллельные линии всюду равно удалены друг от друга" или "любые три точки, не расположенные на одной прямой, принадлежат окружности". Ближе всех подошел к цели иезуит, логик и математик Дж.Саккери (1667-1733), который начал свои исследования с так называемого четырехугольника Саккери (рис. 2), т.е. с четырехугольника BCED, у которого BC = DE, а углы при вершинах C и E прямые. Заметив, что углы при вершинах B и D обязательно равны, Саккери рассмотрел поочередно три гипотезы: верхние углы четырехугольника тупые, прямые и острые. Он доказал, что любая из этих гипотез, если ее принять для какого-нибудь одного такого четырехугольника, остается в силе для всех таких четырехугольников. Саккери намеревался обосновать гипотезу о том, что верхние углы прямые, доказав, что любая другая гипотеза приводит к противоречию. Вскоре он отверг гипотезу о тупом угле (и тем самым лишил себя возможности открыть эллиптическую геометрию), поскольку, как и все геометры до 1854, рассматривал второй постулат как утверждение о том, что прямая имеет бесконечную длину, и отказываться от этого постулата он не хотел. Точно также Саккери в конце концов отверг и гипотезу об остром угле, но прежде, чем принять это ошибочное решение, он, сам того не ведая, открыл многие теоремы геометрии, получившей впоследствии название гиперболической.

Рис. 2. ЧЕТЫРЕХУГОЛЬНИК САККЕРИ - четырехугольник BCED с BC = ED и прямыми углами при вершинах C и E. Евклидова геометрия требует, чтобы углы B и D также были прямыми. В эллиптической геометрии эти углы - тупые, а в гиперболической - острые.
К. Гаусса (1777-1855) принято считать одним из величайших математиков всех времен. Он первым подошел к проблеме с современной точки зрения, согласно которой геометрию, отрицающую пятый постулат, надлежит развивать ради нее самой, не ожидая, что при этом возникнет какое-то противоречие. Письма Гаусса к друзьям говорят о том, что к 1816 он преодолел традиционный предрассудок относительно неизбежности противоречия и развил "антиевклидову" геометрию, удовлетворяющую гипотезе Саккери об остром угле. Но, опасаясь насмешек, он воздерживался от публикации этих идей и тем самым позволил разделить честь открытия гиперболической геометрии (примерно в 1825) венгру Я. Бойяи (1802-1860) и русскому Н. И. Лобачевскому (1793-1856). Бойяи опубликовал свою работу до того, как услышал о Лобачевском, а последний, судя по всему, так никогда и не узнал об исследованиях Бойяи. В 1854 Б. Риман (1826-1866) заметил, что из неограниченности пространства еще не следует его бесконечная протяженность. Смысл этого утверждения станет яснее, если представить, что в неограниченной, но конечной вселенной астроном в принципе мог бы увидеть в телескоп, обладающий достаточно высокой разрешающей способностью, свой собственный затылок (если отвлечься от небольшой детали, связанной с тем, что свет, отраженный от затылка, достиг бы глаза астронома через тысячи миллионов лет). В своем доказательстве того, что внешний угол при любой вершине треугольника больше внутреннего угла при любой из двух остальных вершин, Евклид неявно использовал бесконечную длину прямой. Из этой теоремы тотчас же следует теорема о том, что сумма любых двух углов треугольника меньше суммы двух прямых углов. Если отказаться от бесконечной длины прямой, то гипотеза Саккери о тупом угле становиться верной и из нее следует, что сумма углов треугольника больше суммы двух прямых. Такое положение дел было давно известно в сферической тригонометрии, где стороны треугольника являются дугами больших кругов. Риман внес эпохальный вклад, распространив представление о конечном, но неограниченном пространстве с двух на три и большее число измерений.
Эллиптическая плоскость. Ф. Клейн (1849-1925) первым увидел, как избавить сферическую геометрию от одного из ее недостатков - того, что две лежащие в одной плоскости "прямые" (два больших круга на сфере) имеют не одну общую точку, а две (рис. 3,а). Так как для каждой точки существует одна-единственная точка-антипод (диаметрально противоположная точка), а для любой фигуры существует ее дубликат из точек-антиподов, мы можем, ничем не жертвуя, но многое приобретая, абстрактно отождествить обе точки такой пары, объединив их в одну. Таким образом можно изменить смысл термина "точка", условившись впредь называть "одной точкой" пару диаметрально противоположных точек. Иначе говоря, точки так называемой "эллиптической" плоскости представлены на единичной сфере парами точек-антиподов или диаметрами, соединяющими точки-антиподы. Вся эллиптическая прямая замкнута, как окружность, но, поскольку каждая из ее точек представлена двумя точками-антиподами на единичной сфере, полная длина эллиптической прямой равна половине длины окружности большого круга, т.е. ее полная длина равна p.
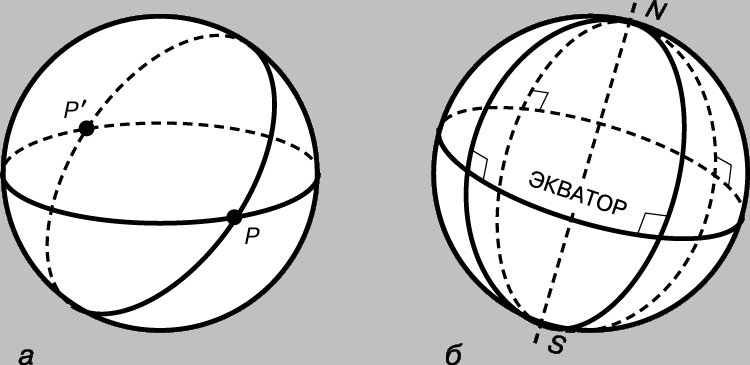
Рис. 3. а - на эллиптической плоскости "точка" представлена двумя точками-антиподами на сфере, например, точками P и P'. б - диаметр, соединяющий северный и южный полюсы сферы, на эллиптической плоскости является "полюсом" экватора.
Такое представление с помощью диаметров и диаметральных плоскостей сферы (при котором диаметр, соединяющий северный и южный полюсы сферы, является "полюсом" экватора), показывает, что все свойства действительной проективной плоскости сохраняются и для эллиптической плоскости.
Геометрия порядка. Один из подходов к построению гиперболической геометрии исходит из некоторых фундаментальных аксиом порядка, справедливых и в евклидовой, но не в эллиптической геометрии. Если считать "точки" исходными понятиями, то запись [[ABC]] означает, что точка B лежит "между" точками A и C (это первичное отношение мы принимаем, не пытаясь его определить). Первые четыре аксиомы порядка утверждают, что 1) существует по крайней мере две точки; 2) если A и B - две различные точки, то существует по крайней мере одна точка C, для которой [[ABC]]; 3) эта точка C отлична от точки A и 4) порядок [[ABC]] влечет за собой [[CBA]], но не [[BCA]]. "Отрезок" AB, по определению, состоит из точек P, для которых [[APB]], а "луч" A/B ("исходящий из A в другую сторону, чем B") - из точек Q, для которых [[QAB]]. "Прямая" AB состоит из отрезка AB, точек A, B и двух лучей A/B, B/A. Пятая аксиома утверждает, что если C и D - различные точки на прямой AB, то A лежит на прямой CD (из этой же аксиомы следует, что прямые AB и CD совпадают). Шестая аксиома дает нам точку вне данной прямой, а седьмая, сформулированная М. Пашем (1843-1931), позволяет определить плоскость как множество всех точек, коллинеарных с парами точек на одной или двух сторонах данного треугольника.
Абсолютная геометрия. Большая часть вклада Бойяи связана с теми разделами гиперболической геометрии, которые принадлежат и евклидовой геометрии. Его "абсолютная геометрия" может быть выведена из геометрии порядка, если к последней добавить еще одно фундаментальное отношение, а именно "конгруэнтность". Это отношение определяется пятью аксиомами типа "Если ABC и A'B'C' - два треугольника, таких, что BC є B'C', CA є C'A', AB є A'B', а D и D' - еще две точки, такие, что [[BCD]] и [[B'C'D']] и BD є B'D', то AD є A'D'". Эти аксиомы служат основой теории длины и позволяют распространить отношение конгруэнтности с пар точек на углы. Определив обычным образом окружность, мы можем рассматривать первые четыре постулата Евклида как теоремы и доказать его первые двадцать восемь предложений, заменив слово "параллельные" на "не пересекающиеся". Однако необходимо тщательно избегать любого обращения к нашему обычному представлению о сумме углов треугольника; например, мы не можем более утверждать, что углы, опирающиеся на один и тот же сегмент окружности, равны, так как доказательство этого предложения зависело бы от суммы углов треугольника. С другой стороны, мы можем доказать, что три высоты остроугольного треугольника пересекаются в одной точке, построить теорию правильных многоугольников и правильных многогранников (с небольшими оговорками). Уточнив понятие параллельности (определив как параллельные лучи, которые просто не пересекаются), мы можем показать, что параллельность - отношение симметричное и транзитивное (т. е. если прямая r параллельна прямой s, то s параллельна r; если r параллельна s, а s параллельна t, то r параллельна t). Множество прямых, параллельных данному лучу, называется "пучком параллельных"; он содержит единственную прямую, проходящую через любую заданную точку. Следуя аналогии с обычным пучком (состоящим из всех прямых, проходящих через точку), мы можем считать, что пучок параллельных определяет "бесконечно удаленную точку", или, по терминологии Д. Гильберта (1862-1943), "конец". Вместо того, чтобы говорить, что два луча (или две прямые) параллельны или что они принадлежат некоторому пучку параллельных M, мы говорим, что два луча имеют общий конец M. Луч, проходящий через точку C и принадлежащий данному пучку параллельных, принято обозначать CM, как если бы это был отрезок; тот же символ CM можно использовать и для обозначения всей прямой. Если BM и CM - параллельные лучи, то фигура MCB называется "асимптотическим треугольником", поскольку она во многом ведет себя, как обычный треугольник. В частности, два асимптотических треугольника конгруэнтны, если у них имеется по конгруэнтной стороне и конгруэнтному углу.
Гиперболическая плоскость. Из абсолютной геометрии Бойяи можно вывести евклидову геометрию, добавив евклидову (или аффинную) аксиому: через точку B, не лежащую на данной прямой r, можно провести не более одной прямой, параллельной данной. Гиперболическую геометрию можно вывести из абсолютной геометрии, добавив гиперболическую аксиому, повторяющую только что приведенную, но без отрицания "не" во втором случае. Таким образом, лучи BM и BN на рис. 4 могут быть оба параллельны r, а если M и N их концы, то r называется "прямой MN". Любая прямая, например t, являющаяся продолжением стороны угла РNBM, образует с r пару "гиперпараллельных", т.е. пару прямых, которые не пересекаются и не параллельны. Две такие прямые имеют единственный общий перпендикуляр. Множество прямых, перпендикулярных данной прямой a, называются "пучком гиперпараллельных" с "осью" a.
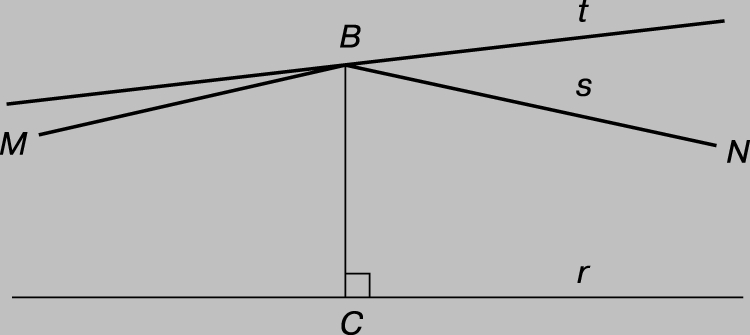
Рис. 4. ЛЮБАЯ ПОЛУПРЯМАЯ, например t, являющаяся продолжением стороны угла NBM, образует с r пару "гиперпараллельных", т.е. две прямые, которые не пересекаются и не параллельны.
Отражение относительно BC показывает, что РCBM и РNBC - равные острые углы. Лобачевский назвал каждый из них "углом параллельности" П(a), где a - длина BC. Он показал, что функция П(a) монотонно убывает от p ¤ 2 до 0, когда a возрастает от 0 до беск. Треугольник BMN естественно назвать "дважды асимптотическим треугольником". Два дважды асимптотических треугольника конгруэнтны, если имеют конгруэнтные углы. Если отрезок CB возрастает до тех пор, пока не превратится в луч CL, то BMN превращается в "трижды асимптотический треугольник" LMN, все три вершины которого являются концами (все три стороны такого треугольника бесконечны, а все три угла равны нулю). Все трижды асимптотические треугольники конгруэнтны. Одной из самых прекрасных страниц в литературе по неевклидовой геометрии со времен Лобачевского считается предложенное Г.Либманом доказательство того, что площадь треугольника остается конечной, когда две (или три) его стороны становятся бесконечными. Доказательство сводится к разбиению асимптотического треугольника на бесконечную последовательность конечных треугольников и перекладыванию их с соблюдением одного условия: все они должны умещаться внутри некоторого конечного пятиугольника. Метод Либмана восполняет один из двух недостающих шагов в предложенном Гауссом красивом доказательстве того, что площадь любого треугольника пропорциональна его "угловому дефекту" - величине, показывающей, насколько сумма углов треугольника меньше двух прямых. Аналогия с выражением (A + B + C) - p для площади сферического треугольника (на единичной сфере) наводит на мысль о естественной единице измерения, при которой площадь треугольника ABC просто равна p - (A + B + C). Используя эту единицу, Лобачевский выразил угол параллельности, соответствующий расстоянию x, формулой П(x) = 2arctg e-x.
Кривые, ортогональные обычному пучку прямых, имеют вид концентрических окружностей; кривые, ортогональные пучку параллельных, имеют вид концентрических "орициклов". В действительности орицикл - это предельная форма окружности, центр которой уходит в бесконечность (так, что диаметры окружности становятся параллельными).
Евклидовы модели неевклидовых геометрий. Ф. Вахтер (1792-1817) за несколько месяцев до безвременной кончины сообщил в письме к Гауссу о своем наблюдении: если пятый постулат Евклида ложен, то сфера, радиус которой стремиться к бесконечности, приближается к предельной поверхности, чья внутренняя геометрия совпадает с геометрией евклидовой плоскости. Тем самым Вахтер предвосхитил появление "орисферы", сыгравшей важную роль в работах Бойяи и Лобачевского. Эта поверхность получается при вращении орицикла вокруг любого из его диаметров. Кривые на орисфере, которые ведут себя, как евклидовы прямые, - орициклы, по которым орисферу пересекают ее диаметральные плоскости. А. Пуанкаре (1854-1912) открыл представление гиперболического пространства с помощью конформной модели, в которой геометрическое место концов имеет вид плоскости W в евклидовом пространстве, а сферам с центрами в W соответствуют плоскости гиперболического пространства. Заменив сферы полусферами, Пуанкаре получил возможность представить все гиперболическое пространство с помощью половины евклидова пространства, а именно всеми точками, лежащими по одну сторону от W. Один пучок концентрических орисфер представлен плоскостями, параллельными W; можно доказать, что евклидовы расстояния в такой плоскости пропорциональны соответствующим геодезическим на орисфере, что полностью согласуется с наблюдением Вахтера. Рассматривая сечение трехмерной модели Пуанкаре плоскостью, перпендикулярной W, мы получим модель аналогичную модели Пуанкаре для гиперболической плоскости. В этой модели геометрическое место концов имеет вид евклидовой прямой. В другой модели геометрическое место концов имеет вид окружности w, а прямые на гиперболической плоскости - дуг окружностей, ортогональных w. Две параллельные дуге r, проходящие через точку B, - просто дуги, проходящие через точку B и касающиеся дуги r в ее концах, как на рис. 5.
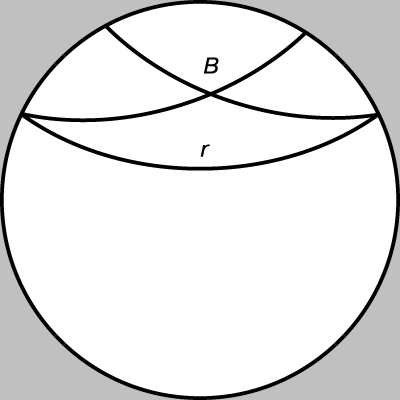
Рис. 5. ПАРАЛЛЕЛЬНЫЕ BC и BD к r, проходящие через точку B, - это просто две дуги, проходящие через точку B так, что они касаются r в ее концах. Эта модель "конформна", так как углы сохраняются, хотя расстояния неизбежно искажаются.
Такая модель называется "конформной" потому, что углы сохраняют свою величину, хотя расстояния неизбежно искажаются. Если пойти на искажение углов, то дуги можно заменить хордами, как на рис. 6. Эту более простую модель предложил в 1868 году Э. Бельтрами (1835-1900) для доказательства того, что гиперболическая геометрия так же логически непротиворечива, как и евклидова (хотя и Бойяи и Лобачевский были интуитивно убеждены, что их исследования никогда не приведут к двум противоречащим друг другу утверждениям, ни один из них не дожил до строгого доказательства непротиворечивости гиперболической геометрии). В модели Бельтрами множество прямых, проходящих через точку A, представлено обычным пучком параллельных или гиперпараллельных в зависимости от того, находится ли A внутри w, на w или вне w. В последнем случае (см. нижнюю часть рис. 6) ось пучка гиперпараллельных есть "поляра" точки A, соединяющая точки касания двух касательных, проведенных из точки A. Иначе говоря, две перпендикулярные прямые гиперболической плоскости представлены двумя прямыми, "сопряженными" относительно w. Такого рода идеи относятся к проективной геометрии; действительно, w можно рассматривать как коническое сечение на действительной проективной плоскости; в этом случае мы приходим к модели А.Кэли (1821-1895) и Ф. Клейна. Это коническое сечение w, геометрическое место концов, есть то, что Кэли назвал "абсолютом". (Преисполненный энтузиазмом, он сначала даже писал это слово с прописной буквы "А", но позднее перешел на строчную "а" во избежание упрека в непочтительности). Чтобы быть совершенно точным, следует отметить, что проективная плоскость, на которой работал Кэли, была не действительной, а комплексной: Кэли разрешал w быть коническим сечением, не содержащим действительных точек, отчего геометрия становится не гиперболической, а эллиптической.
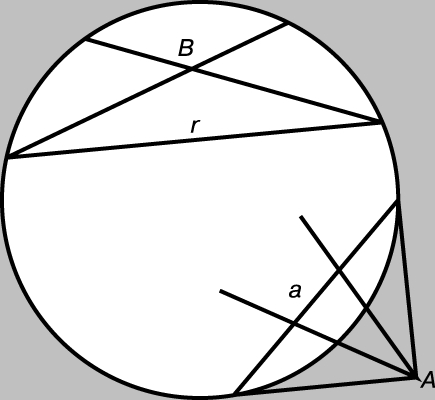
Рис. 6. В ЭТОЙ КОНФОРМНОЙ МОДЕЛИ, если мы согласимся, что углы также искажаются, дуги, изображенные на рис. 5, можно заменить их хордами. В нижней части рисунка ось пучка параллельных - "поляра" точки A, соединяющая точки касания двух касательных, проведенных из A.
Орфографический словарь
Полезные сервисы
неевклидовы геометрии
Энциклопедический словарь
Неевкли́довы геоме́трии - геометрические системы, отличные от евклидовой геометрии. Среди неевклидовой геометрии особое значение имеет Лобачевского геометрия.
* * *
НЕЕВКЛИДОВЫ ГЕОМЕТРИИ - НЕЕВКЛИ́ДОВЫ ГЕОМЕ́ТРИИ, геометрические системы, отличные от евклидовой геометрии. Среди неевклидовых геометрий особое значение имеет Лобачевского геометрия (см. ЛОБАЧЕВСКОГО ГЕОМЕТРИЯ).
Большой энциклопедический словарь
НЕЕВКЛИДОВЫ ГЕОМЕТРИИ - геометрические системы, отличные от евклидовой геометрии. Среди неевклидовых геометрий особое значение имеет Лобачевского геометрия.
Полезные сервисы
неедлы
неедлы (nejedly) вит
Большой энциклопедический словарь
НЕЕДЛЫ (Nejedly) Вит (1912-45) - чешский композитор и дирижер. Сын З. Неедлы. В 1940-43 музыкальный редактор Всесоюзного радио в Москве. Основатель и руководитель чехословацкого армейского ансамбля (с 1945 им. Неедлы). Опера "Ткачи" (1938), кантата "День", 3 симфонии, массовые песни.
Полезные сервисы
неедлы вит
Энциклопедический словарь
Не́едлы Вит (Nejedly) (1912-1945), чешский композитор и дирижёр. Сын З. Неедлы. В 1940-1943 музыкальный редактор Всесоюзного радио в Москве. Основатель и руководитель чехословацкого армейского ансамбля (с 1945 имени Неедлы). Опера «Ткачи» (1938), кантата «День», 3 симфонии, массовые песни.
* * *
НЕЕДЛЫ Вит - НЕ́ЕДЛЫ (Nejedly) Вит (1912-45), чешский композитор и дирижер. Сын З. Неедлы. В 1940-43 музыкальный редактор Всесоюзного радио в Москве. Основатель и руководитель чехословацкого армейского ансамбля (с 1945 им. Неедлы). Опера «Ткачи» (1938), кантата «День», 3 симфонии, массовые песни.
Полезные сервисы
неедлы зденек
Энциклопедический словарь
Не́едлы Зденек (1878-1962), первый президент Чехословацкой АН (с 1952); член Чешской академии наук и искусств (1907), иностранный член-корреспондент АН СССР (1947). Труды по истории Чехословакии, СССР, истории культуры, чешской литературе и музыке. В 1935-1945 жил в Москве.
* * *
НЕЕДЛЫ Зденек - НЕ́ЕДЛЫ Зденек (1878-1962), чешский ученый, 1-й президент Чехословацкой АН (с 1952), иностранный член-корреспондент АН СССР (1947). Труды по истории Чехословакии, СССР, истории культуры, чешской литературе и музыке.
Большой энциклопедический словарь
НЕЕДЛЫ Зденек (1878-1962) - чешский ученый, 1-й президент Чехословацкой АН (с 1952), иностранный член-корреспондент АН СССР (1947). Труды по истории Чехословакии, СССР, истории культуры, чешской литературе и музыке.
Полезные сервисы
неезжалая
неезженный
неезженый
Толковый словарь Ожегова
НЕЕ́ЗЖЕНЫЙ, -ая, -ое; -ен, -ена. Такой, по к-рому не ездили или мало ездят, ездили. Неезженые просёлки.
Энциклопедический словарь
НЕЕ́ЗЖЕНЫЙ -ая, -ое.
1. Не приученный к езде (о лошади). Н. конь.
2. Такой, по которому давно не ездили, мало ездили; ненаезженный. Н. путь. Н-ая дорога.
Академический словарь
-ая, -ое.
1. Не приученный к езде.
[Федор:] Да, отец! Он русский! И русский он обычай перенял: Он на пути к Москве, себе в забаву, Смирял неезженых коней! А. К. Толстой, Царь Борис.
2. Такой, по которому давно не ездили, мало ездили; ненаезженный.
Кое-где сквозь чащу виднелись болотца. В колеях неезженой дороги росло много грибов. Паустовский, Повесть о лесах.
Слитно. Раздельно. Через дефис
Орфографический словарь
Формы слов для слова неезженый
нее́зженый, нее́зженая, нее́зженое, нее́зженые, нее́зженого, нее́зженой, нее́зженых, нее́зженому, нее́зженым, нее́зженую, нее́зженою, нее́зжеными, нее́зженом, нее́зжен, нее́зжена, нее́зжено, нее́зжены, нее́зженее, понее́зженее, нее́зженей, понее́зженей
Морфемно-орфографический словарь
Грамматический словарь
Полезные сервисы
неела
Толковый словарь Даля
Синонимы к слову неела
сущ., кол-во синонимов: 8
невезунчик (12)
несчастливец (31)
неудача (125)
неудачник (56)
неёла (1)
развисляй (5)
рохля (48)
тюфяк (41)
Полезные сервисы
неелов
Словарь русских фамилий
НЕЁЛОВ
Сколько поклонников у замечательной нашей актрисы Марины Неёловой! Ее артистическая судьба блистательна! Между тем фамилия ей досталась со смыслом прямо противоположным. Костромичи, например, говоря неёла, имеют в виду неудачу. И человек, у которого все идет прахом, ничего не получается, ничего не клеится, получал прозвище Неёла, которое впоследствии и стало фамилией. По сути, «однофамильцами» Неёлова кроме Неёлина являются Невдахин, Невдачин, Неудахин, Неудачин.
НЕВДАХИН НЕЕЛОВ НЕУДАХИН НЕУДАЧИН
Правы те Нееловы, которые вместо второго е в своей фамилии пишут ё: происходит она от костромского неёла - "неудатный, нерасторопный", как объясняет в своем словаре В И. Даль. (Ф). В старину существовало русское слово неёла - "неудача", оно могло стать основой прозвища. (Н) Родственные фамилии - Невдахин, Неудахин, Неудачин. (Э) В "Ономастиконе" Веселовского Неел, Неелов: Семен Неел, холоп боярина Тучка Морозова, 1481 г.; Нееловы, XVIЧXVII вв., Новгород и Дорогобуж Неел, неела Ч неудача, неудачливый Неудача: Неудача Цыплятов Монастырев первая половина XVI в , его сын Никита Неудачин, дворецкий новгородского владыки, казнен в 1570 г ; Иван Евстафьевич Неудача Плещеев
НЕЁЛОВ
Сколько поклонников у замечательной нашей актрисы Марины Неёловой! Ее артистическая судьба блистательна! Между тем фамилия ей досталась со смыслом прямо противоположным. Костромичи, например, говоря неёла, имеют в виду неудачу. И человек, у которого все идет прахом, ничего не получается, ничего не клеится, получал прозвище Неёла, которое впоследствии и стало фамилией. По сути, «однофамильцами» Неёлова кроме Неёлина являются Невдахин, Невдачин, Неудахин, Неудачин.
Полезные сервисы
неёлова
Сканворды для слова неёлова
- Марина из «Осеннего марафона».
- Эта актриса сыграла разные роли в двух экранизациях пьесы Шварца «Тень».
- Российская актриса, исполнившая роль Нины в фильме «Монолог».
- Российская актриса, исполнившая роль Аллы в фильме «Осенний марафон».
- Российская актриса, исполнившая роль Валентины Костиной в фильме «Слово для защиты».
- Российская актриса, исполнившая роль принцессы и дочери трактирщика в фильме «Старая, старая сказка».
- Российская актриса, исполнившая роль Александры в фильме «Фантазии Фарятьева».
Полезные сервисы
неёлова мар. мстиславовна
Гуманитарный словарь
НЕЁЛОВА Мар. Мстиславовна (род. 1947) - актриса. В 1969 окончила ЛГИТМиК (класс В. В. Меркурьева). Работала в Моск. т-ре им. Моссовета, сыграла роль в сп. "Турбаза" (реж. А. В. Эфрос). С 1974 Н. работает в Моск. т-ре "Современник". Дебютировала в роли Валентины в сп. "Валентин и Валентина" (1974). С тех пор театр. карьера Н. связана с этим т-ром, где она сыграла в гл. ролях в работах Г. Б. Волчек и др. режиссеров. Роли Н. в "Современнике": Вероника ("Вечно живые", 1975), Виола ("Двенадцатая ночь", 1975), Люба ("Фантазии Фарятьева", 1976), Аня ("Вишневый сад", 1976), Маша ("Три сестры", 1982), Марья Антоновна ("Ревизор", 1986), Ханни ("Кто боится Вирджинии Вульф", 1988), Лора ("Звезды на утреннем небе", 1988), Евгения Гинзбург ("Крутой маршрут", 1989), Анфиса ("Анфиса", 1991), Паулина ("Смерть и дева", 1992), Вальтрауте ("Адский сад", 1993), Раневская ("Вишневый сад", 1997) и др.
Кинематографическую деят-ность Н. начала в студенческие годы, снявшись на "Ленфильме" в ф. Н. Н. Кошеверовой "Старая, старая сказка" (1968). Среди ее киноролей - Аннунциата ("Тень", 1971), Нина ("Монолог", 1972), Лейда ("Сломанная подкова", 1973), Стеша ("С тобой и без тебя", 1973), Костина ("Слово для защиты", 1977), Алла ("Осенний марафон", 1979), Александра ("Фантазии Фарятьева", 1979), Елена Сергеевна ("Дорогая Елена Сергеевна", 1988), Юлия Джули ("Тень", 1991), Анна Андреевна ("Ревизор", 1996) и др.
В т-ре и в кино сыграла целую вереницу интеллигентных сов. женщин - нервных, скромных, соединяющих достоинство с беззаветностью и безответностью. Игра Н., как и ее героини, нервна и иронична одновременно. Редкое умение плакать на сцене и на экране: тихо, глотая слезы, и надрывно, с воплями, некрасиво, но всегда выразительно. Сцены слез всегда центральные, ударные в ее ролях.
Полезные сервисы
неёлова марина мстиславовна
Энциклопедический словарь
Неёлова Марина Мстиславовна (р. 1947), актриса, народная артистка РСФСР (1987). С 1974 в Московском театре «Современник». Игре свойственны непосредственность и страстность, нервная порывистость при тщательной психологической проработке роли: Вероника («Вечно живые» В. С. Розова), Люба («Фантазии Фарятьева» А. Н. Соколовой), Оля («Спешите делать добро» М. М. Рощина), Евгения Семёнова («Крутой маршрут» по Е. С. Гинзбург), Анфиса («Анфиса» Л. Н. Андреева), Раневская («Вишнёвый сад» А. П. Чехова) и др. Снималась в фильмах: «Монолог», «Слово для защиты», «Осенний марафон», «Тюремный романс» и др.
* * *
НЕЕЛОВА Марина Мстиславовна - НЕЕЛОВА Марина Мстиславовна (р. 8 января 1947, Ленинград), российская актриса, народная артистка России (1987). С 1974 в Московском театре «Современник». Блестящая исполнительница характеров еще неустойчивых, полудетских, на переломе юности, игре свойственны непосредственность и страстность, нервная порывистость при тщательной психологической проработке роли. Вероника («Вечно живые» В. С. Розова, 1974), Люба («Фантазии Фарятьева» А. Н. Соколовой, 1977), Оля («Спешите делать добро» М. И. Рощина, 1980), Евгения Семенова («Крутой маршрут» по Е. С. Гинзбург, 1989), Анфиса («Анфиса» Л. Н. Андреева, 1991). Снималась в фильмах: «Монолог» (1972), «Слово для защиты» (1976), «Осенний марафон» (1979), «Тюремный роман», «Ты у меня одна» (оба - 1993, премия «Ника-93») и др. Государственная премия СССР (1990).
* * *
НЕЕЛОВА Марина Мстиславовна (р. 8 января 1947, Ленинград), российская актриса театра и кино, народная артистка России (1987), Государственная премия РСФСР (1981, 2001).
Яркое драматическое дарование
В 1969 окончила Ленинградский институт театра, музыки и кино. Будучи студенткой, дебютировала в кино в лирико-комедийных ролях Принцессы и Дочери Трактирщика («Старая, старая сказка», 1970). Первые роли актрисы в кино были сказочно-романтичными («Тень», «Принц и нищий», оба - 1972; «Сломанная подкова», 1974) или лирическими («Цвет белого снега», 1970; «Ждем тебя, парень!», 1973). Яркое драматическое дарование актрисы, ее способность проявлять искренние чувства на пределе человеческих эмоций раскрылись в роли Нины в кинокартине «Монолог» (1973). В кино Нееловой блестяще удается воплощать образы ранимых, хрупких, незащищенных героинь, которые тем не менее упрямо отстаивают личную независимость - Степанида Базырина («С тобой и без тебя», 1974), Саша Неродова («Просто Саша», 1976), Валентина Костина («Слово для защиты», 1977), Нина Георгиевна («Фотографии на стене», 1978), Алла («Осенний марафон», 1979, Государственная премия РСФСР за 1981).
В театре, кино и на телевидении
В театре (с 1973 в Современнике (см. МОСКОВСКИЙ ТЕАТР СОВРЕМЕННИК)) актриса, выступившая в качестве травести («Четыре капли», «Спешите делать добро»), скоро перешла с лирико-комедийного (Виола в «Двенадцатой ночи») и мелодраматического амплуа (Валентина в «Валентине и Валентине») к нервному и ломкому рисунку в ролях Вероники в «Вечно живых» и Ники в спектакле «Из записок Лопатина». Естественно и с чувством стиля Неелова играла в телевизионных экранизациях зарубежной классики («Ночь ошибок», «Домби и сын»). На телевидении актриса выступала в блестящем дуэте с Андреем Мироновым (см. МИРОНОВ Андрей Александрович) в спектакле «Между небом и землей» и в телефильме «Фантазии Фарятьева» (1979). Мотив «некоммуникабельности чувств» несхожих людей развит в телефильме «Транзит» (1982), где Марина Неелова выступила в паре с Михаилом Ульяновым (см. УЛЬЯНОВ Михаил Александрович).
Утвердив себя в драматическом амплуа, актриса вновь испытала склонность к лирической комедии или легкому фарсу («Красавец-мужчина», 1978; «Дамы приглашают кавалеров», 1981; «Карусель», 1983; «Чужая жена и муж под кроватью», 1984; «Мы веселы, счастливы, талантливы», 1987). Снимаясь в последующие годы все реже, Неелова чередует современные драматические («Дорогая Елена Сергеевна», 1988; «Ты у меня одна», 1993, премия «Ника») и костюмно-исторические трагикомические образы («Тень, или Может быть, все обойдется», 1991, телефильм «Ревизор», 1996; «Сибирский цирюльник», 1999). В театре же актриса сконцентрировалась на драматическом, а порой и трагическом материале («Анфиса», «Крутой маршрут», «Три сестры», «Вишневый сад», «Играем... Шиллера!»).
В 2002 актриса снялась в телесериале «Азазель».
Полезные сервисы
неелова марина мстиславовна
Большой энциклопедический словарь
НЕЕЛОВА Марина Мстиславовна (р. 1947) - российская актриса, народная артистка России (1987). С 1974 в Московском театре "Современник". Блестящая исполнительница характеров еще неустойчивых, полудетских, на переломе юности, игре свойственны непосредственность и страстность, нервная порывистость при тщательной психологической проработке роли. Вероника ("Вечно живые" В. С. Розова, 1974), Люба ("Фантазии Фарятьева" А. Н. Соколовой, 1977), Оля ("Спешите делать добро" М. И. Рощина, 1980), Евгения Семенова ("Крутой маршрут" по Е. С. Гинзбург, 1989), Анфиса ("Анфиса" Л. Н. Андреева, 1991). Снималась в фильмах: "Монолог", "Слово для защиты", "Осенний марафон", "Тюремный роман" и др.
Полезные сервисы
неёлова, марина мстиславовна
Иллюстрированный энциклопедический словарь

М.М. Неёлова (слева) и М.Б. Терехова в фильме "Монолог".
Неелова, Марина Мстиславовна
НЕЁЛОВА Марина Мстиславовна (родилась в 1947), актриса. С 1974 в Московском театре "Современник". Блестящая исполнительница характеров еще неустойчивых, полудетских, на переломе юности. Игре свойственны непосредственность и страстность, нервная порывистость при тщательной психологической проработке роли: Вероника ("Вечно живые" В.С. Розова, 1974), Люба ("Фантазии Фарятьева" А.Н. Соколовой, 1977), Оля ("Спешите делать добро" М.М. Рощина, 1980), Евгения Семеновна ("Крутой маршрут" по Е.С. Гинзбург, 1989), Анфиса ("Анфиса" Л.Н. Андреева, 1991). Снималась в фильмах: "Монолог" (1973), "Слово для защиты" (1977), "Осенний марафон" (1979) и др.

Марина Неёлова и Олег Даль в фильме "Тень".

Марина Неёлова в фильме "Слово для защиты".
Полезные сервисы
нееловы
Энциклопедический словарь
Нее́ловы - российские архитекторы, представители раннего классицизма. Василий Иванович (1721/1722 - 1782). Работы - пейзажный «Английский сад» (1771-1780), неоготическое «Адмиралтейство» (1773-1777) в Царском Селе (ныне г. Пушкин). Его сын Илья Васильевич (1745-1793). Работы - корпус Лицея (1788-1792), павильоны «Верхняя ванна» и «Нижняя ванна» (1777-1779), там же.
* * *
НЕЕЛОВЫ - НЕЕЛОВЫ, российские архитекторы, представители раннего классицизма (см. КЛАССИЦИЗМ) :
1) Василий Иванович (1721/22-82) - пейзажный «Английский сад» (1771-80), псевдоготическое «Адмиралтейство» (1773-77) в г. Пушкин;
2) его сын Илья Васильевич (1745-93) - корпус Лицея (1788-92), павильоны «Верхняя ванна» и «Нижняя ванна» (1777-79), там же.
Большой энциклопедический словарь
НЕЕЛОВЫ - российские архитекторы, представители раннего классицизма: 1) Василий Иванович (1721/22-82) - пейзажный "Английский сад" (1771-80), псевдоготическое "Адмиралтейство" (1773-77) в г. Пушкин;
2) его сын Илья Васильевич (1745-93) - корпус Лицея (1788-92), павильоны "Верхняя ванна" и "Нижняя ванна" (1777-79), там же.
Полезные сервисы
неёловы
Гуманитарный словарь
НЕЁЛОВЫ - архитекторы, строители дворцово-паркового ансамбля в Царском Селе.
Вас. Ив. (1721-82), помощник С. И. Чевакинского и В. В. де Растрелли, в 1770 командирован в Англию для знакомства с пейзажным паркостроением. Разработал проект пейзажной части Екатерининского парка (1771-80, садоводы Д. Буш, Т. Ильин); построил Мраморный мост (1773-74, по образцу моста в Уилтонхауз, Англия, сооруж. по проекту А. Палладио); Большой каприз в китайском стиле (1772); Адмиралтейство (1773-83) и Эрмитажную кухню (1775) в англо-голландской готике (1773-83).
Ил. Вас. сын предыдущ. (1745-93): учился в АХ и в Риме (1770-74). Построил Нижнюю ванну (1777-79), великокняжеский корпус (1788-92, перестроен для Лицея, 1811, В. П. Стасов), придворцовую часть Александровского парка (1792-96), Баболовский дворец (1783-85).
Петр Вас. (1749-1848), ездил с отцом в Англию, занимал должность царскосельского арх. в 1810-20-е гг.
Полезные сервисы
неель
неель (nÉel) луи эжен феликс
неель луи эжен феликс
Энциклопедический словарь
Нее́ль Луи Эжен Феликс (Néel) (р. 1904), французский физик, иностранный член РАН (1958). Предсказал (1932) антиферромагнетизм, разработал его теорию, создал теорию ферритов. Нобелевская премия (1970).
* * *
НЕЕЛЬ Луи Эжен Феликс - НЕЕ́ЛЬ Луи Эжен Феликс (22 ноября 1904, Лион, Франция - 17 ноября 2000), французский физик, иностранный член РАН (1991; иностранный член АН СССР с 1958). Предсказал (1932) антиферромагнетизм, разработал его теорию, создал теорию ферритов. Нобелевская премия (1970).
Большой энциклопедический словарь
НЕЕЛЬ Луи Эжен Феликс (р. 1904) - французский физик, иностранный член РАН (1991; иностранный член АН СССР с 1958). Предсказал (1932) антиферромагнетизм, разработал его теорию, создал теорию ферритов. Нобелевская премия (1970).
Полезные сервисы
нееля точка
Энциклопедический словарь
Нее́ля то́чка (антиферромагнитная точка Кюри), температура (θN, TN), выше которой исчезает спонтанная намагниченность антиферромагнетиков и они становятся парамагнетиками (фазовый переход II рода). Названа по имени Л. Нееля.
* * *
НЕЕЛЯ ТОЧКА - НЕЕ́ЛЯ ТО́ЧКА (антиферромагнитная точка Кюри), температура (QN, TN), выше которой исчезает спонтанная намагниченность антиферромагнетиков и они становятся парамагнетиками (фазовый переход II рода). Названа по имени Л. Нееля.
Большой энциклопедический словарь
НЕЕЛЯ точка (антиферромагнитная точка Кюри) - температура (QN, TN), выше которой исчезает спонтанная намагниченность антиферромагнетиков и они становятся парамагнетиками (фазовый переход II рода). Названа по имени Л. Нееля.
Полезные сервисы
неемия
неергор (neergaard) нильс
Большой энциклопедический словарь
НЕЕРГОР (Нергор) (Neergaard) Нильс (1854-1936) - премьер-министр Дании в 1908-1909 и 1920-24; историк и экономист. В 1908-13 (с перерывами) и 1926-29 министр финансов. Один из лидеров партии Венстре (первоначально - с 1901 - ее левого крыла).
Полезные сервисы
неергор нергор (neergaard) нильс
неергор нильс
Энциклопедический словарь
Не́ергор Нильс - Нергор (Neergaard) (1854-1936), премьер-министр Дании в 1908-1909 и 1920-1924; историк и экономист. В 1908-1913 (с перерывами) и 1926-1929 министр финансов. Один из лидеров партии Венстре (первоначально - с 1901 - её левого крыла).
* * *
НЕЕРГОР Нильс - НЕ́ЕРГОР (Нергор) (Neergaard) Нильс (1854-1936), премьер-министр Дании в 1908-1909 и 1920-24; историк и экономист. В 1908-13 (с перерывами) и 1926-29 министр финансов. Один из лидеров партии Венстре (первоначально - с 1901 - ее левого крыла).
Полезные сервисы
неестественно
Толковый словарь
I нареч. качеств.
1. Не будучи свойственным естественной природе вещей.
отт. перен. Выходя за пределы нормального; необычно.
2. перен.
Деланно, фальшиво, неискренне.
II предик.
1. Оценочная характеристика ситуации, чьих-либо действий как не отличающихся естественностью, не представляющихся обычными, нормальными.
2. перен.
Оценочная характеристика чьих-либо действий как фальшивых, неискренних.
Академический словарь
нареч. к неестественный (во 2 знач.).
- Ну, что тебе опять? - спросила Луша неестественно спокойно, как в конторе, когда ее отрывали от дел. С. Антонов, Тетя Луша.
[Борис] держался как-то скованно и неестественно: то беспричинно смеялся, зажимая рот кулаком, то с испугом оглядывался и прислушивался к каждому шагу за дверью. Закруткин, Сотворение мира.
Слитно. Раздельно. Через дефис
Орфографический словарь
Синонимы к слову неестественно
нареч, кол-во синонимов: 39
анормально (11)
аффектированно (7)
болезненно (22)
выделанно (1)
выдуманно (6)
вымученно (9)
вычурно (21)
деланно (8)
жеманно (9)
извращенно (14)
искусственно (18)
манерно (17)
наигранно (14)
напряженно (34)
нарочито (17)
насильственно (16)
натужно (15)
натянуто (14)
неадекватно (6)
невероятно (94)
неискренне (16)
неискренно (14)
ненатурально (8)
ненормально (28)
необычно (40)
неправильно (50)
патологически (7)
принужденно (16)
противоестественно (13)
сверхъестественно (22)
странно (46)
странновато (7)
театрально (7)
уродливо (17)
условно (6)
фальшиво (21)
ходульно (11)
экзотично (6)
1. ненатурально, принуждённо, деланно, нарочито; выделанно (устар.)
/ вести себя: искусственно, наигранно, натянуто, театрально, аффектированно
/ улыбаться, смеяться: насильственно
// улыбаться: напряжённо, натянуто, вымученно
см. также жеманно
2. см. ненормально
принужденно, сверхъестественно, наигранно, патологически, аффектированно, экзотично, противоестественно, уродливо, ходульно, анормально, выдуманно, манерно, натянуто, вычурно, ненормально, болезненно, театрально, неискренно, вымученно, необычно, условно, нарочито, извращенно, искусственно, неискренне, противонатурально, странновато, ненатурально, выделанно, деланно, напряженно, насильственно, невероятно, неправильно, жеманно, странно
Антонимы к слову неестественно
Полезные сервисы
неестественной смертью погибнуть
неестественность
Толковый словарь
Толковый словарь Ожегова
Академический словарь
-и, ж.
Свойство по прил. неестественный (во 2 знач.).
Неестественность голоса. Неестественность походки.
◊
[Каренин] чувствовал непрочность и неестественность своих отношений с женою. Л. Толстой, Анна Каренина.
Орфографический словарь
Формы слов для слова неестественность
неесте́ственность, неесте́ственности, неесте́ственностей, неесте́ственностям, неесте́ственностью, неесте́ственностями, неесте́ственностях
Синонимы к слову неестественность
сущ., кол-во синонимов: 49
аномалия (43)
анормальность (17)
аффектация (12)
болезненность (39)
выделанность (2)
выдуманность (9)
вымученность (6)
вычурность (24)
деланность (16)
дефективность (15)
жеманничанье (10)
жеманность (15)
жеманство (14)
извращенность (27)
изломанность (24)
искусственность (24)
манерность (24)
надрыв (15)
наигранность (17)
наигрыш (3)
напряжение (45)
напряженность (51)
нарочитость (19)
натужность (6)
натяжка (7)
натянутость (17)
неадекватность (17)
неискренность (25)
ненатуральность (12)
ненормальность (54)
необычность (40)
неполноценность (20)
неправдоподобие (7)
неправильность (53)
несоответствие (35)
отклонение от нормы (18)
патология (25)
принужденность (19)
раздутость (10)
сверхъестественность (16)
странность (69)
театральность (9)
уродливость (37)
фальшивость (34)
фальшь (36)
ходульность (10)
экзотика (13)
экзотичность (6)
1. ненатуральность, принуждённость, деланность; выделанность (устар.)
/ о поведении: нарочитость, искусственность, наигранность, натянутость, театральность, изломанность, аффектация
/ об улыбке: напряжённость, натянутость, вымученность
см. также жеманство
2. см. ненормальность
ненормальность, противоестественность, необычность, странность, ненатуральность, принужденность, деланность, нарочитость, искусственность, наигранность, натянутость, театральность, изломанность, аффектация, напряжённость, натянутость; ходульность, напряженность, уродливость, напряжение, выдуманность, фальшь, жеманство, дефективность, экзотика, болезненность, патология, анормальность, манерность, вычурность, раздутость, аномалия, наигрыш, извращенность, отклонение от нормы, несоответствие, жеманничанье, неискренность, жеманность, выделанность, неадекватность, экзотичность, сверхъестественность, вымученность, неправильность, неполноценность, надрыв. Ant. естественность, нормальность, обычность, обыкновенность
НЕЕСТЕСТВЕННОСТЬ
НЕЕСТЕСТВЕННОСТЬ, деланость, ненатуральность, принужденность, устар. выделанность
НЕЕСТЕСТВЕННЫЙ, деланый, ненатуральный, принужденный, устар. выделанный
НЕЕСТЕСТВЕННО, делано, нарочито, ненатурально, принужденно, устар. выделанно
Тезаурус русской деловой лексики
1.
Syn: ненормальность, противоестественность (усил.), необычность, странность
Ant: естественность, нормальность, обычность, обыкновенность
2.
Syn: ненатуральность, принужденность, деланность, нарочитость, искусственность, наигранность, натянутость, театральность, изломанность, аффектация, напряженность, натянутость