ТРЕТЬЯК ТОПОЛЕВ

Фамилия образована от некрестильного имени или прозвища Тополь. Имена от названий растений, в частоности деревьев, были распространены у славян. (Э)

Составить слова из слова тополев

прил.

Видом напоминающий тополь.

тополеви́дный; кратк. форма -ден, -дна

Составить слова из слова тополевидный

сущ., кол-во синонимов: 1

Составить слова из слова тополёвник

сущ., кол-во синонимов: 2

Составить слова из слова тополевник

то/полево-и/вовый

Составить слова из слова тополево-ивовый

то/полево-и/льмовый

Составить слова из слова тополево-ильмовый

прил.

1. соотн. с сущ. тополь, связанный с ним

2. Свойственный тополю, характерный для него.

3. Состоящий из тополей.

ТО́ПОЛЕВЫЙ, тополевая, тополевое. прил. к тополь.

ТО́ПОЛЬ, -я, мн. -я́, -е́й и (устар.) -и, -ей, м. Дерево сем. ивовых с высоким и прямым стволом. Серебристый т. Пирамидальный т.

ТО́ПОЛЕВЫЙ, ТОПОЛЁК; ТОПОЛИ́НЫЙ см. То́поль.

-ая, -ое.

прил. к тополь.

Тополевая ветка. Тополевая аллея.

◊

Гранин всеми легкими вдыхал пряные запахи тополевых почек. Рудный, Гангутцы.

то́полевый и тополёвый

то́полевый

то́полевый (не рекомендуется тополёвый).

то́полевый, то́полевая, то́полевое, то́полевые, то́полевого, то́полевой, то́полевых, то́полевому, то́полевым, то́полевую, то́полевою, то́полевыми, то́полевом, то́полев, то́полева, то́полево, то́полевы, то́полевее, пото́полевее, то́полевей, пото́полевей

прил., кол-во синонимов: 2

то́пол/ев/ый и топол/ёв/ый.

то́полевый п 1a [//тополёвый п 1a]

Составить слова из слова тополевый

м. разг.

1. уменьш. к сущ. тополь

2. ласк. к сущ. тополь

тополёк, -лька́

тополёк, топольки́, тополька́, тополько́в, топольку́, тополька́м, тополько́м, тополька́ми, топольке́, тополька́х

тополёк м 3*b

- Повесть Чингиза Айтматова «... мой в красной косынке».

Составить слова из слова тополёк

ТО́ПОЛЕВЫЙ, ТОПОЛЁК; ТОПОЛИ́НЫЙ см. То́поль.

сущ., кол-во синонимов: 2

Составить слова из слова тополек

тополели/стный

Составить слова из слова тополелистный

- Как в Италии называют Микки-Мауса?

Составить слова из слова тополино

прил.

1. соотн. с сущ. тополь, связанный с ним

2. Принадлежащий тополю.

ТО́ПОЛЬ, -я, мн. -я́, -е́й и (устар.) -и, -ей, м. Дерево сем. ивовых с высоким и прямым стволом. Серебристый т. Пирамидальный т.

ТО́ПОЛЕВЫЙ, ТОПОЛЁК; ТОПОЛИ́НЫЙ см. То́поль.

-ая, -ое.

прил. к тополь.

Тополиная роща.

◊

Пахло молодыми тополиными листочками. Федин, Первые радости.

тополи́ный

тополи́ный

тополи́ный, тополи́ная, тополи́ное, тополи́ные, тополи́ного, тополи́ной, тополи́ных, тополи́ному, тополи́ным, тополи́ную, тополи́ною, тополи́ными, тополи́ном, тополи́н, тополи́на, тополи́но, тополи́ны, тополи́нее, потополи́нее, тополи́ней, потополи́ней

прил., кол-во синонимов: 1

тополевый

топол/и́н/ый.

тополи́ный п 1a

Составить слова из слова тополиный

м.

Специалист в области топологии.

ТОПО́ЛОГ, тополога, муж. (спец.). Математик, специалист по топологии.

топо́лог, -а

топо́лог

топо́лог, топо́логи, топо́лога, топо́логов, топо́логу, топо́логам, топо́логом, топо́логами, топо́логе, топо́логах

сущ., кол-во синонимов: 1

топ/о́/лог/.

топо́лог мо 3a

- Математик, занимающийся изучением свойств фигур (или пространств), которые сохраняются при непрерывных деформациях, таких, например, как растяжение, сжатие или изгибание.

- Григорий Перельман как математик-геометр.

- Математик, который не отличает пончик от кофейной кружки.

Составить слова из слова тополог

прил.

1. соотн. с сущ. топология, связанный с ним

2. Свойственный топологии, характерный для неё.

3. Относящийся к топологии.

ТОПОЛОГИ́ЧЕСКИЙ, топологическая, топологическое (мат.). прил. к топология.

-ая, -ое.

прил. к топология.

топологи́ческий

топологи́ческий, топологи́ческая, топологи́ческое, топологи́ческие, топологи́ческого, топологи́ческой, топологи́ческих, топологи́ческому, топологи́ческим, топологи́ческую, топологи́ческою, топологи́ческими, топологи́ческом, топологи́ческ, топологи́ческа, топологи́ческо, топологи́чески

топ/о/лог/и́ческ/ий.

топологи́ческий п 3a✕~

Составить слова из слова топологический

Топологи́ческое простра́нство - математическое понятие, обобщающее понятие метрического пространства. Топологическое пространство - множество элементов любой природы, в котором тем или иным способом определены предельные соотношения.

* * *

ТОПОЛОГИЧЕСКОЕ ПРОСТРАНСТВО - ТОПОЛОГИ́ЧЕСКОЕ ПРОСТРА́НСТВО, математическое понятие, обобщающее понятие метрического пространства. Топологическое пространство - множество элементов любой природы, в котором тем или иным способом определены предельные соотношения.

ТОПОЛОГИЧЕСКОЕ пространство - математическое понятие, обобщающее понятие метрического пространства. Топологическое пространство - множество элементов любой природы, в котором тем или иным способом определены предельные соотношения.

Составить слова из слова топологическое пространство

ж.

Раздел математики, изучающий качественные свойства геометрических фигур, не зависящие от их длины, величины углов, прямолинейности и т.п.

ТОПОЛО́ГИЯ, топологии, мн. нет, жен. (от греч. topos - место и logos - учение) (мат.). Часть геометрии, исследующая качественные свойства фигур (т.е. не зависящие от таких понятий, как длина, величина углов, прямолинейность и т.п.).

ТОПОЛО́ГИЯ -и; ж. [от греч. topos - место и logos - учение] Раздел математики, изучающий наиболее общие свойства геометрических фигур, не изменяющиеся при любых деформациях.

◁ Топологи́ческий, -ая, -ое. Т-ие свойства фигуры. Т. факт.

* * *

тополо́гия (от греч. tópos - место и ...логия), раздел математики, изучающий топологические свойства фигур, то есть свойства, не изменяющиеся при любых деформациях, производимых без разрывов и склеиваний (точнее, при взаимно однозначных и непрерывных отображениях). Примерами топологических свойств фигур являются размерность, число кривых, ограничивающих данную область, и т. д. Так, окружность, эллипс, контур квадрата имеют одни и те же топологические свойства, так как эти линии могут быть деформированы одна в другую описанным выше образом; в то же время кольцо и круг обладают различными топологическими свойствами: круг ограничен одним контуром, а кольцо - двумя.

* * *

ТОПОЛОГИЯ - ТОПОЛО́ГИЯ (от греч. topos - место и logos - слово, учение), раздел математики, изучающий топологические свойства фигур, т. е. свойства, не изменяющиеся при любых деформациях, производимых без разрывов и склеиваний (точнее, при взаимно однозначных и непрерывных отображениях). Примерами топологических свойств фигур являются размерность, число кривых, ограничивающих данную область. Так, окружность, эллипс, контур квадрата имеют одни и те же топологические свойства, т. к. эти линии могут быть деформированы одна в другую описанным выше образом; в то же время кольцо и круг обладают различными топологическими свойствами: круг ограничен одним контуром, а кольцо - двумя.

ТОПОЛОГИЯ (от греч. topos - место и ...логия) - раздел математики, изучающий топологические свойства фигур, т. е. свойства, не изменяющиеся при любых деформациях, производимых без разрывов и склеиваний (точнее, при взаимно однозначных и непрерывных отображениях). Примерами топологических свойств фигур являются размерность, число кривых, ограничивающих данную область, и т. д. Так, окружность, эллипс, контур квадрата имеют одни и те же топологические свойства, т. к. эти линии могут быть деформированы одна в другую описанным выше образом; в то же время кольцо и круг обладают различными топологическими свойствами: круг ограничен одним контуром, а кольцо - двумя.

-и, ж.

Раздел математики, изучающий наиболее общие свойства геометрических фигур, не изменяющиеся при любых деформациях.

[От греч. τόπος - место и λόγος - учение]

ТОПОЛОГИЯ - раздел математики, занимающийся изучением свойств фигур (или пространств), которые сохраняются при непрерывных деформациях, таких, например, как растяжение, сжатие или изгибание. Непрерывная деформация - это деформация фигуры, при которой не происходит разрывов (т.е. нарушения целостности фигуры) или склеиваний (т.е. отождествления ее точек). Такие геометрические свойства связаны с положением, а не с формой или величиной фигуры. В отличие от евклидовой и римановой геометрий, геометрии Лобачевского и других геометрий, занимающихся измерением длин и углов, топология имеет неметрический и качественный характер. Раньше она носила названия "анализ ситус" (анализ положения), а также "теория точечных множеств". В научно-популярной литературе топологию часто называют "геометрией на резиновом листе", поскольку ее наглядно можно представлять себе как геометрию фигур, нарисованных на идеально упругих резиновых листах, которые подвергаются растяжению, сжатию или изгибанию. Топология - один из новейших разделов математики.

История. В 1640 французский математик Р.Декарт (1596-1650) нашел инвариантное соотношение между числом вершин, ребер и граней простых многогранников. Это соотношение Декарт выразил формулой V - E + F = 2, где V - число вершин, E - число ребер и F - число граней. В 1752 швейцарский математик Л. Эйлер (1707-1783) дал строгое доказательство этой формулы. Еще один вклад Эйлера в развитие топологии - это решение знаменитой задачи о кенигсбергских мостах. Речь шла об острове на реке Прегель в Кенигсберге (в том месте, где река разделяется на два рукава - Старый и Новый Прегель) и семи мостах, соединяющих остров с берегами. Задача состояла в том, чтобы выяснить, можно ли обойти все семь мостов по непрерывному маршруту, побывав на каждом только один раз и вернувшись в исходную точку. Эйлер заменил участки суши точками, а мосты - линиями. Полученную конфигурацию Эйлер назвал графом, точки - его вершинами, а линии - ребрами. Вершины он разделил на четные и нечетные в зависимости от того, четное или нечетное число ребер выходит из вершины. Эйлер показал, что все ребра графа можно обойти ровна по одному разу по непрерывному замкнутому маршруту, лишь если граф содержит только четные вершины. Так как граф в задаче о кенигсбергских мостах содержит только нечетные вершины, мосты невозможно обойти по непрерывному маршруту, побывав на каждом ровно по одному разу и вернувшись к началу маршрута. Предложенное Эйлером решение задачи о кенигсбергских мостах зависит только от взаимного расположения мостов. Оно положило формальное начало топологии как разделу математики. К.Гаусс (1777-1855) создал теорию узлов, которой позднее занимались И.Листинг (1808-1882), П. Тэйт (1831-1901) и Дж. Александер. В 1840 А. Мебиус (1790-1868) сформулировал так называемую проблему четырех красок, которую впоследствии исследовали О. де Морган (1806-1871) и А. Кэли (1821-1895). Первым систематическим трудом по топологии были Предварительные исследования по топологии Листинга (1874). Основателями современной топологии являются Г. Кантор (1845-1918), А. Пуанкаре (1854-1912) и Л. Брауэр (1881-1966).

Разделы топологии. Топологию можно подразделить на три области: 1) комбинаторную топологию, изучающую геометрические формы посредством их разбиения на простейшие фигуры, регулярным образом примыкающие друг к другу; 2) алгебраическую топологию, занимающуюся изучением алгебраических структур, связанных с топологическими пространствами, с упором на теорию групп; 3) теоретико-множественную топологию, изучающую множества как скопления точек (в отличие от комбинаторных методов, представляющих объект как объединение более простых объектов) и описывающую множества в терминах таких топологических свойств, как открытость, замкнутость, связность и т.д. Разумеется, такое деление топологии на области в чем-то произвольно; многие топологи предпочитают выделять в ней другие разделы.

Некоторые основные понятия. Топологическое пространство состоит из множества точек S и набора S подмножеств множества S, удовлетворяющего следующим аксиомам: (1) все множество S и пустое множество принадлежат набору S; (2) объединение любой совокупности множеств из S есть множество из S; (3) пересечение любого конечного числа множеств из S есть множество из S. Множества, входящие в набор S, называются открытыми множествами, а сам этот набор - топологией в S.

См. МНОЖЕСТВ ТЕОРИЯ. Топологическое преобразование, или гомеоморфизм, одной геометрической фигуры S на другую, S', - это отображение (p (r) p') точек p из S в точки p' из S', удовлетворяющее следующим условиям: 1) устанавливаемое им соответствие между точками из S и S' взаимно однозначно, т.е. каждой точке p из S соответствует только одна точка p' из S' и в каждую точку p' отображается только одна точка p; 2) отображение взаимно непрерывно (непрерывно в обе стороны), т.е. если заданы две точки p, q из S и точка p движется так, что расстояние между ней и точкой q стремится к нулю, то расстояние между соответствующими точками p', q' из S' также стремится к нулю, и наоборот. Геометрические фигуры, переходящие одна в другую при топологических преобразованиях, называются гомеоморфными. Окружность и граница квадрата гомеоморфны, так как их можно перевести друг в друга топологическим преобразованием (т.е. изгибанием и растяжением без разрывов и склеиваний, например, растяжением границы квадрата на описанную вокруг него окружность). Сфера и поверхность куба также гомеоморфны. Чтобы доказать гомеоморфность фигур, достаточно указать соответствующее преобразование, но тот факт, что для каких-то фигур найти преобразование нам не удается, не доказывает, что эти фигуры не гомеоморфны. Здесь помогают топологические свойства.

Рис. 1. ПОВЕРХНОСТЬ КУБА И СФЕРА гомеоморфны, т.е. могут быть переведены друг в друга топологическим преобразованием, но ни поверхность куба, ни сфера не гомеоморфны тору (поверхности "бублика").

Топологическим свойством (или топологическим инвариантом) геометрических фигур называется свойство, которым вместе с данной фигурой обладает также любая фигура, в которую она переходит при топологическом преобразовании. Любое открытое связное множество, содержащее по крайней мере одну точку, называется областью. Область, в которой любую замкнутую простую (т.е. гомеоморфную окружности) кривую можно стянуть в точку, оставаясь все время в этой области, называется односвязной, а соответствующее свойство области - односвязностью. Если же некоторую замкнутую простую кривую этой области нельзя стянуть в точку, оставаясь все время в этой области, то область называется многосвязной, а соответствующее свойство области - многосвязностью. Представьте себе две круговые области, или диски, одну без дыр, а другую с дырами. Первая область односвязна, вторая многосвязна. Односвязность и многосвязность - топологические свойства. Область с дырой не может перейти при гомеоморфизме в область без дыр. Интересно отметить, что если в многосвязном диске провести по разрезу от каждой из дыр до края диска, то он станет односвязным. Максимальное число замкнутых простых непересекающихся кривых, по которым можно разрезать замкнутую поверхность, не разделяя ее на отдельные части, называется родом поверхности. Род - топологический инвариант поверхности. Можно доказать, что род сферы равен нулю, род тора (поверхности "бублика") - единице, род кренделя (тора с двумя дырками) - двум, род поверхности с p дырами равен p. Отсюда следует, что ни поверхность куба, ни сфера не гомеоморфны тору. Среди топологических инвариантов поверхности можно также отметить число сторон и число краев. Диск имеет 2 стороны, 1 край и род 0. Тор имеет 2 стороны, не имеет краев, а его род равен 1. Введенные выше понятия позволяют уточнить определение топологии: топологией называется раздел математики, изучающий свойства, которые сохраняются при гомеоморфизмах.

Важные проблемы и результаты. Теорема Жордана о замкнутой кривой. Если на поверхности проведена простая замкнутая кривая, то существует ли какое-либо свойство кривой, которое сохраняется при деформации поверхности? Существование такого свойства вытекает из следующей теоремы: простая замкнутая кривая на плоскости делит плоскость на две области, внутреннюю и внешнюю. Эта кажущаяся тривиальной теорема очевидна для кривых простого вида, например, для окружности; однако для сложных замкнутых ломаных дело обстоит иначе. Теорема была впервые сформулирована и доказана К.Жорданом (1838-1922); однако доказательство Жордана оказалось ошибочным. Удовлетворительное доказательство было предложено О.Вебленом (1880-1960) в 1905.

Теорема Брауэра о неподвижной точке. Пусть D - замкнутая область, состоящая из окружности и ее внутренности. Теорема Брауэра утверждает, что для любого непрерывного преобразования, переводящего каждую точку области D в точку этой же области, существует некоторая точка, которая остается неподвижной при этом преобразовании. (Преобразование не предполагается взаимно однозначным.) Теорема Брауэра о неподвижной точке представляет особый интерес потому, что она, по-видимому, является, наиболее часто используемой в других разделах математики топологической теоремой.

Проблема четырех красок. Проблема заключается в следующем: можно ли любую карту раскрасить в четыре цвета так, чтобы любые две страны, имеющие общую границу, были раскрашены в различные цвета? Проблема четырех красок топологическая, так как ни форма стран, ни конфигурация границ не имеют значения. Гипотеза о том, что четырех красок достаточно для соответствующей раскраски любой карты, была впервые высказана в 1852. Опыт показал, что четырех красок действительно достаточно, но строгого математического доказательства не удавалось получить на протяжении более ста лет. И только в 1976 К.Аппель и В. Хакен из Иллинойского университета, затратив более 1000 часов компьютерного времени, добились успеха.

Односторонние поверхности. Простейшей односторонней поверхностью является лист Мебиуса, названный так в честь А. Мебиуса, открывшего его необычайные топологические свойства в 1858. Пусть ABCD (рис. 2,а) - прямоугольная полоска бумаги. Если склеить точку A с точкой B, а точку C с точкой D (рис. 2,б), то получится кольцо с внутренней поверхностью, наружной поверхностью и двумя краями. Одну сторону кольца (рис. 2,б) можно окрасить. Окрашенная поверхность будет ограничена краями кольца. Жук может совершить "кругосветное путешествие" по кольцу, оставаясь либо на окрашенной, либо на неокрашенной поверхности. Но если полоску перед склеиванием концов перекрутить на полоборота и склеить точку A с точкой C, а B с D, то получится лист Мебиуса (рис. 2,в). У этой фигуры есть только одна поверхность и один край. Любая попытка окрасить только одну сторону листа Мебиуса обречена на неудачу, так как у листа Мебиуса всего одна сторона. Жук, ползущий по середине листа Мебиуса (не пересекая края), вернется в исходную точку в положении "вверх ногами". При разрезании листа Мебиуса по средней линии он не распадается на две части.

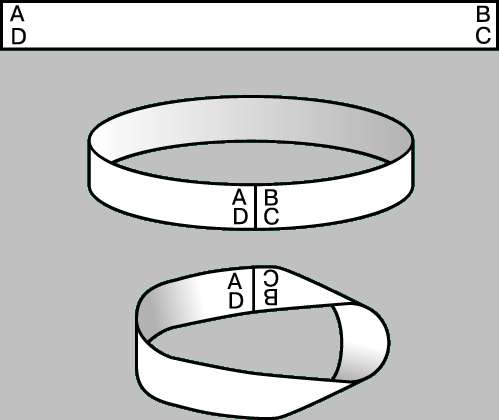
Рис. 2. СКЛЕЕННАЯ В КОЛЬЦО ПОЛОСКА (б) имеет внутреннюю и внешнюю стороны и два края. Лист Мебиуса (в), склеенный из перекрученной на полоборота прямоугольной полоски (а), имеет только одну сторону и один край.

Узлы. Узел можно представлять себе как запутанный кусок тонкой веревки с соединенными концами, расположенный в пространстве. Простейший пример - из куска веревки сделать петлю, пропустить один из ее концов сквозь петлю и соединить концы. В результате мы получим замкнутую кривую, которая остается топологически той же самой, как бы ее ни растягивать или скручивать, не разрывая и не склеивая при этом отдельные точки. Проблема классификации узлов по системе топологических инвариантов пока не решена.

ЛИТЕРАТУРА

Ху Сы-цзян. Теория гомотопий. М., 1964 Куратовский А. Топология, тт. 1-2. М., 1966, 1969 Спеньер Э. Алгебраическая топология. М., 1971 Александров П.С. Введение в теорию множеств и общую топологию. М., 1977 Келли Дж. Общая топология. М., 1981

тополо́гия, -и

тополо́гия, -и

тополо́гия, тополо́гии, тополо́гий, тополо́гиям, тополо́гию, тополо́гией, тополо́гиею, тополо́гиями, тополо́гиях

сущ., кол-во синонимов: 1

топ/о/ло́г/и/я [й/а].

тополо́гия ж 7a

Наука, учение о местностях.

- Этот раздел математики утверждает, что бублик и кружка - одно и то же.

- Раздел математики.

- Эту науку часто называют геометрией на резиновом листе.

- Наука о свойствах геометрических фигур.

- Способ объединения компьютеров между собой в сети.

Составить слова из слова топология

Топология письма (термин взят из математики; от греч. τόπος «место») - видоизменение форм письменных знаков под влияние разных факторов (времени, материала письма, культурных и эстетических традиций и т.д.). Топология - наука о путях, расстояниях и направлениях, изучающая феномен непрерывности и трансформаций без склеивания и разрывов. Важную роль играет ориентация в пространстве и понятия левое-правое (сравните R и Я).

Если две (или более) формально различные графемы происходят из одной, то они наз. гомеоморфами: Aaα>α. Образование из одной формы буквы другой наз. вариативной способностью. Т.е. в некоторых случаях можно с большой долей вероятности сделать вывод о невозможности топологического перехода от одной формы буквы к другой: W ≠ О ≠ Т

Гомеоморфами не обязательно должны быть буквы родственные фонетически: еэ, но C>O>Q>Ω

Составить слова из слова топология письма

▲ строение (чего)

↑ фигура

топология - математическая наука о непрерывности.

топологические инварианты: связность. компактность. размерность.

род поверхности - натуральное число, характеризующее связность замкнутой поверхн.

разрывность.

шар - тело, получающееся при вращении круга вокруг своего диаметра.

тор. тороид.

ручка. | решетка.

топологическое пространство.

↓ непрерывный, отверстие, отверстие (в теле), край

сторона поверхности

см. переплетение

Составить слова из слова топология фигуры

м.

1. Календарный - с точки зрения друидов - период зоны влияния одной из священных звёзд, определённого божества и данного дерева.

2. перен.

Тот, кто рождён в такой временной период (4 - 8 февраля и 5 - 13 августа).

ТО́ПОЛЬ, тополя, мн. тополи-тополя, муж., и (устар., редк.) ТОПОЛЬ, тополи, жен. Дерево сем. ивовых, разных видов. Серебристый тополь. Белый тополь. Пирамидальный тополь (разновидность осокоря). Черный тополь (то же, что осокорь). «Чуть трепещут сребристых тополей листы.» Пушкин. «Тополи, стеснившись в ряд, качая тихо головою, как судьи, шепчут меж собою.» Пушкин. «За тополью высокою я вижу там окно.» Лермонтов.

ТО́ПОЛЬ, -я, мн. -я, -ей и (устар.) -и, -ей, муж. Дерево сем. ивовых с высоким и прямым стволом. Серебристый т. Пирамидальный т.

| прил. тополевый, -ая, -ое и тополиный, -ая, -ое. Тополевая аллея. Тополиный пух (на цветущем тополе).

·об. дерево Populus, разных видов, особ. P. alba, белый тополь, и порода его P. nivea, серебристый тополь, P. balsamifera, такамагака, пахучий, душистый тополь, P. laurifolia, осокорь душистая, алтайская, рай-дерево. P. nigra; черный тополь, осокорь, сухара, папорт. P. pyramidalis, пирамидальный, итальянский тополь, раина. Топольник муж. тополевая роща. Тополевое дерево дрябло и плохо, а потому почти в поделки не идет. Топальный запах.

ТО́ПОЛЬ, -я, мн тополя́ и то́поли,м

Лиственное дерево семейства ивовых с высоким прямым стволом, глянцевитыми пятилопастными листьями и с цветками, свисающими в виде сережек.

Уж не будут листвою крылатой надо мною звенеть тополя (С. Есенин).

ТО́ПОЛЬ -я; мн. тополя́ и то́поли; м. Дерево сем. ивовых с высоким прямым стволом, с глянцевитыми листьями различной формы и с цветками, свисающими в виде цилиндрических серёжек. Серебристый т. Пирамидальный т. (разновидность такого стройного, высокого дерева, крона которого имеет форму пирамиды).

◁ Тополёк, -лька́; м. Уменьш.-ласк. Молодой т. То́полевый; тополи́ный, -ая, -ое. Т. запах. Т-ые почки. Т. пух. Т-ая роща (состоящая из тополей). Т-ая лодка (сделанная из древесины тополя).

* * *

то́поль - род деревьев семейства ивовых. Свыше 100 (по другим данным, около 30) видов, в Северном полушарии; в России 10-15 видов. Лесообразующая порода. В культуре как декоративные тополь белый, осокорь, или тополь чёрный, тополь пирамидальный и др. Древесина мягкая, используется в бумажном, спичечном производстве и пр.

* * *

ТОПОЛЬ - ТО́ПОЛЬ, род деревьев семейства ивовых. Св. 100 (по другим данным, ок. 30) видов, в Северном полушарии; в России 10-15 видов. Лесообразующая порода. В культуре выращивают как декоративные: тополь белый, осокорь, или тополь черный, тополь пирамидальный и др. Древесина мягкая, используется в бумажном, спичечном производстве и пр.

ТОПОЛЬ - род деревьев семейства ивовых. Св. 100 (по другим данным, ок. 30) видов, в Северном полушарии; в России 10-15 видов. Лесообразующая порода. В культуре выращивают как декоративные: тополь белый, осокорь, или тополь черный, тополь пирамидальный и др. Древесина мягкая, используется в бумажном, спичечном производстве и пр.

-я, мн. тополя́ и то́поли, м.

Дерево сем. ивовых, с высоким прямым стволом, с глянцевитыми листьями различной формы и с цветками, свисающими в виде сережек.

Серебристый тополь.

◊

На Бибиковском бульваре распускались клейкие пирамидальные тополя. Паустовский, Далекие годы.

ТОПОЛЬ (Populus), насчитывающий ок. 35 видов род быстрорастущих, короткоживущих деревьев семейства ивовых (Salicaceae). Родина - Северное полушарие, где тополи произрастают от Арктики до субтропиков. Размеры варьируют от средних до крупных: у многих видов максимальная высота порядка 30 м, а диаметр ствола достигает 2,4 м. Для тополя характерны бледная бархатистая кора молодых побегов и шершавая, глубоко растрескавшаяся - старых стволов. Листья широкие на длинных черешках. Цветки в цилиндрических сережках распускаются весной раньше листьев: на одних деревьях тычиночные (мужские), на других - пестичные (женские). Коробочковидный плод содержит многочисленные мелкие семена, покрытые длинными шелковистыми волосками (тополиный пух) и разносимые ветром. Тополь бальзамический (P. balsamifera, или P. tacamahaca) произрастает от Лабрадора до Чукотки, от Новой Англии до Северной Дакоты и в Скалистых горах. Он часто встречается вдоль рек в прериях северо-запада Канады и является самым крупным деревом американской Субарктики. Высота его до 27 м, листья толстые, яйцевидные, длиной до 13 см. Нижняя сторона белая.

ТОПОЛЬ БАЛЬЗАМИЧЕСКИЙ родом с севера Северной Америки. У этого дерева широкие листья и мелкие опушенные семена, созревающие в коробочковидных плодах.

Тополь крупнолистный (P. candicans, или P. balsamifera var. subcordata) произрастает в провинциях Ньюфаундленд, Квебек, Онтарио (Канада), доходя на юге до штатов Мичиган, Нью-Йорк и Мэн. На северо-востоке США его широко разводят как декоративную породу. Возможно, это разновидность или гибрид тополя бальзамического - они очень похожи. Тополь дельтовидный (P. deltoides) произрастает островками от запада Новой Англии до юга Саскачевана (Канада), доходя до Техаса и Флориды. Обычен вдоль рек. В высоту достигает 27 м. Листья треугольные, длиной 7-15 см, с крупными закругленными зубцами, черешок уплощенный. Молодые веточки желтые. Это дерево обеспечивало первых европейских колонистов топливом, легко обрабатываемой древесиной и прохладной тенью.

ТОПОЛЬ ДЕЛЬТОВИДНЫЙ - быстрорастущее дерево, распространенное от юга Канады по всему востоку США.

Тополь волосистоплодный (P. trichocarpa) распространен от Аляски до севера Мексики. В бассейне Паджет-Саунд его высота достигает 68 м: это самое крупное лиственное дерево тихоокеанского северо-запада США. Широко-яйцевидные листья длиной 12-25 см заострены на верхушке, снизу гладкие. У них мелкозубчатый край и округлые в сечении черешки. Тополь Саржента (P. sargentii) - крупное дерево Великих равнин и восточной окраины Скалистых гор, растущее в США и Канаде. Его высота до 27 м. Этот вид похож на тополь дельтовидный, отличается пушистыми почками и более светлыми молодыми веточками. Ширина его крупнозубчатых листьев часто больше их длины, а у основания листовой пластинки находятся железки. Тополь белый, или серебристый (P. alba), тополь черный, или осокорь (P. nigra), и его хорошо известная разновидность - тополь пирамидальный (var. italica) - евразиатские виды, натурализовавшиеся на востоке США и Канады. Тополь белый достигает высоты более 27 м. У него яйцевидные опущенные листья длиной до 12 см с округло-зубчатыми или лопастными краями. Их нижняя сторона белая или серая. Высота осокоря до 27 м; у него треугольные листья длиной до 10 см со светло-зеленой нижней поверхностью. Характерная черта тополя пирамидального - узкая столбовидная форма кроны. Несколько тополей с характерной "дрожащей" листвой выделяются в неформальную группу "осин": черешок их листьев тонкий, уплощенный и очень гибкий, поэтому легкая бумажистая листовая пластинка вздрагивает при малейшем движении воздуха. Собственно осина, или тополь дрожащий (P. tremula), - лесная порода севера Евразии. Высота дерева до 15-18 м; листья с закругленными зубцами. Тополь осинообразный (P. tremuloides) обладает самым широким среди всех американских деревьев ареалом и встречается от Лабрадора до Юкона, на юге доходит до Кентукки, а по горам - до Мексики. Это дерево обычно во всех провинциях Канады. Оно, как правило, мелкое, но может достигать 30 м высоты. Листья почти округлые, мелкозубчатые. Зимующие почки блестящие. Кора молодых экземпляров желтовато-зеленая или почти белая, а у старых - от темно-бурой до черной. Этот вид важен для естественного лесовозобновления: он первым поселяется на вырубках и гарях, быстро растет и защищает своим пологом всходы более долговечных пород-доминантов. Тополь крупнозубчатый (P. grandidentata), также из группы осин, - высокое (до 23 м) прямое дерево. Ареал у него уже, чем у предыдущего вида: от Новой Шотландии до юго-востока Манитобы (Канада), а на юге - до Северной Каролины и Теннесси. Тополя осинообразный и крупнозубчатый часто образуют смешанные древостои, но первый отличается более крупными и толстыми крупнозубчатыми листьями. У всех трех этих "осин" известны плакучие разновидности. Все тополя легко размножаются вегетативно (корневыми отпрысками, черенками, кольями), широко используются как почво- и водозащитные, а некоторые виды - как декоративные и озеленительные деревья. Древесина тополя умеренно-мягкая, светлая, довольно легкая, непрочная (особенно низка ударопрочность). Идет в основном на изготовление ящиков и упаковочных клетей, внутренних частей мебели, деревянной посуды, корыт, кадок для упаковки масла и других продовольственных товаров, на производство бумаги, набивочной стружки и спичек.

Тополь чёрный: 1 - побег с мужской сережкой; 2 - побег с женской сережкой; 3 - лист.

ТОПОЛЬ, род листопадных деревьев (семейство ивовые). Свыше 100 (по другим данным, около 30) видов, в Северном полушарии. В России около 20 видов, включая осину. Высота 30 - 45 м, недолговечны (лишь некоторые доживают до 150 - 200 лет). Быстрорастущая неприхотливая порода. Широко используется для озеленения: разводят главным образом мужские особи, т.к. тополиный "пух" (мелкие семена с волосками) женских особей засоряет улицы и вызывает у многих аллергию. Древесина мягкая, используется в бумажном, спичечном производстве и др. Настой коры и почек тополя черного применяется в народной медицине (противовоспалительное и жаропонижающее действие).

Ля-ля тополя. Жарг. мол. Шутл. 1. Пустой разговор, болтовня. 2. Обман. Максимов, 233.

Три тополя на Плющихе. Жарг. шк. Шутл.-ирон. Школьная линейка. По названию кинофильма. ВМН 2003, 134.

см.: ляля

то́поль, -я, мн. ч. -я́, -е́й

то́поль, -я; мн. тополя́, -е́й

то́поль, м., род. то́поля (устарелое то́поль, ж., род. то́поли); мн. тополя́, род. тополе́й и то́поли, то́полей.

то́поль, тополя́, то́поля, тополе́й, то́полю, тополя́м, то́полем, тополя́ми, то́поле, тополя́х

сущ., кол-во синонимов: 8

осина, серебристый тополь, осокорь, тополек

высокий (Апухтин, Белоусов); голенастый (Сергеев-Ценский); длинный (Бальмонт); серебристый (Тургенев, Суриков, Пушкин); стройный (Белоусов); тонкий (Гиппиус)

то́поль/.

то́поль м 2c① [поэтич. также м 2a]

Общеславянское слово, соответствующее латинскому populus с тем же значением.

Общеслав. Происхождение неясно. Обычно связывают с лат. populus «тополь» с диссимиляцией p - p > т - п.

то́поль

род. п. -я, м., укр. топо́ля, др.-русск. тополь м., собир. тополиɪе ср. р., цслав. тополь ж. λεύκη, болг. топо́ла, сербохорв. топо̀ла, словен. tорólа, чеш. tороl м., слвц. tороl᾽ м., польск. tороlа, tороl ж., в.-луж., н.-луж. tороɫ.

Предполагают связь с лат. pōpulus ж. "тополь" и диссимиляцию р - р > t - р (см. Нидерман, IF 26, 59), далее - родство с греч. πτελέα ж. "вяз", эпидаврск. πελέα - то же, греч. άπελλόν . αἴγειρος; см. Вальде - Гофм. 2, 340; Мейе - Эрну 924. Заимствование из лат. было бы возможно, если бы можно было исходить из ср.-лат. papulus, как в случае с д.-в.-н. papilboum, ср.-в.-н. рареl "тополь" (см. Клюге-Гётце 431; Вальде - Гофм.; Мейе - Эрну, там же); так, напр., Брюкнер 573; но вост. часть территории ром. языков имеет форму *plōp(u)lus : рум. рlор, алб. рlер, ит. рiорро (см. М.-Любке 552 и сл.); ср. Мi. ЕW 358; LР 997; Младенов 636; Голуб - Копечный 387.

- Дерево, устраивающее зиму среди лета.

- Дерево, которое вспоминают после фразы «ля-ля-ля».

- Дерево, вносящее пуховый вклад в аллергию.

- «Пуховое» дерево.

- Дерево, из которого пух летит.

- Дерево на Плющихе.

- Дерево семейства ивовых.

- Осокорь.

- Российский космический корабль.

- Стратегический мобильный комплекс с трёхступенчатой твёрдотопливной межконтинентальной баллистической ракетой РТ-2ПМ.

- Лекарственное растение.

- Баллада украинского писателя Тараса Шевченко.

- Стихотворение Афанасия Фета.

Составить слова из слова тополь

ТОПОЛЬ Эдуард Хаимович - ТО́ПОЛЬ Эдуард Хаимович (р. 1938), русский писатель. С 1978 в эмиграции в США. В романах («Журналист для Брежнева, или Смертельные игры», 1981, «Красная площадь», 1983, оба совместно с Ф. Е. Незнанским (см. НЕЗНАНСКИЙ Фридрих Евсеевич); «Чужое лицо»,1986, «Завтра в России», 1988 и др.), сочетающих факты и вымысел, острые социально-политические коллизии в СССР.

ТОПОЛЬ Эдуард Хаимович (р. 1938) - русский писатель. С 1978 в эмиграции в США. В романах ("Журналист для Брежнева, или Смертельные игры", 1981, "Красная площадь", 1983, оба совместно с Ф. Е. Незнанским; "Чужое лицо",1986, "Завтра в России", 1988 и др.), сочетающих факты и вымысел, острые социально-политические коллизии в СССР.

Составить слова из слова тополь эдуард хаимович