сущ., кол-во синонимов: 1

относчик

Составить слова из слова относитель

ОТНОСИТЕЛЬНАЯ БИОЛОГИЧЕСКАЯ ЭФФЕКТИВНОСТЬ - ОТНОСИ́ТЕЛЬНАЯ БИОЛОГИ́ЧЕСКАЯ ЭФФЕКТИ́ВНОСТЬ излучений, отношение поглощенной дозы стандартного излучения (обычно рентгеновские лучи), вызывающей определенный биологический эффект, к поглощенной дозе рассматриваемого излучения, вызывающей такой же биологический эффект, напр. гибель 50% клеток или мышей.

ОТНОСИТЕЛЬНАЯ БИОЛОГИЧЕСКАЯ ЭФФЕКТИВНОСТЬ излучений - отношение поглощенной дозы стандартного излучения (обычно рентгеновские лучи), вызывающей определенный биологический эффект, к поглощенной дозе рассматриваемого излучения, вызывающей такой же биологический эффект, напр. гибель 50% клеток или мышей.

Составить слова из слова относительная биологическая эффективность

▲ величина

↑ соотношение

относительная величина - величина соотношения, частное двух величин.

градация.

масштаб (# цен). | декремент.

бел. децибел. непер.

эффективность

▼ СТЕПЕНЬ

Составить слова из слова относительная величина (какая)

Относи́тельная вла́жность - отношение упругости водяного пара, содержащегося в воздухе, к упругости насыщенного пара при той же температуре; выражается в процентах.

* * *

ОТНОСИТЕЛЬНАЯ ВЛАЖНОСТЬ - ОТНОСИ́ТЕЛЬНАЯ ВЛА́ЖНОСТЬ, отношение упругости водяного пара (см. УПРУГОСТЬ ВОДЯНОГО ПАРА), содержащегося в воздухе, к упругости насыщенного пара при той же температуре; выражается в процентах.

ОТНОСИТЕЛЬНАЯ ВЛАЖНОСТЬ - отношение упругости водяного пара, содержащегося в воздухе, к упругости насыщенного пара при той же температуре; выражается в процентах.

Составить слова из слова относительная влажность

Относи́тельная высота́ - превышение, разность абсолютных высот какой-либо точки земной поверхности относительно другой точки.

* * *

ОТНОСИТЕЛЬНАЯ ВЫСОТА - ОТНОСИ́ТЕЛЬНАЯ ВЫСОТА́, превышение, разность абсолютных высот (см. АБСОЛЮТНАЯ ВЫСОТА) какой-либо точки земной поверхности относительно другой точки.

ОТНОСИТЕЛЬНАЯ ВЫСОТА - превышение, разность абсолютных высот какой-либо точки земной поверхности относительно другой точки.

Составить слова из слова относительная высота

Относи́тельная погре́шность - см. Погрешность.

* * *

ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ - ОТНОСИ́ТЕЛЬНАЯ ПОГРЕ́ШНОСТЬ, см. Погрешность (см. ПОГРЕШНОСТЬ).

ОТНОСИТЕЛЬНАЯ Погрешность - см. Погрешность.

Составить слова из слова относительная погрешность

Относительная хронология (в лингвистике) - Установление возраста фактов и явлений в истории языка в терминах относительного времени, в соотнесении с другими фактами языковой системы («до» - «после», «раньше» - «позже», «предшествует» - «следует за», а также «вызывает» - «вытекает из», «изменяется в» - «возникает из»)

В сравнительно-историческом языкознании относительная хронология играет более существенную роль, чем абсолютная хронология, поскольку связана с выяснением причинно-следственных отношений между языковыми явлениями.

Составить слова из слова относительная хронология (в лингвистике)

относительная частота - относительная частота словарной единицы получается от деления ее абсолютной частоты на длину текста (корпуса).

Составить слова из слова относительная частота

сущ., кол-во синонимов: 1

Составить слова из слова относительница

I нареч. качеств.-обстоят.

В известной мере, до некоторой степени.

II предл. с род.

Соответствует по значению сл.: в отношении кого-либо или чего-либо, по поводу кого-либо или чего-либо.

ОТНОСИ́ТЕЛЬНО, нареч. (книжн.).

1. Более или менее, до некоторой степени, сравнительно. Опыт прошел относительно удачно.

2. в знач. предлога с род. Что касается, по отношению к кому-чему-нибудь, в отношении чего-нибудь. Относительно хода дела еще ничего нельзя сказать.

ОТНОСИ́ТЕЛЬНО

I. нареч. В известной мере, до некоторой степени; сравнительно. Прыжок о. высокий. Море было о. спокойно. Конец повести о. благополучный.

II. предлог. кого-чего. По отношению к кому-, чему-л., в отношении кого-, чего-л. Симметрия геометрических фигур о. оси. Исполнить свой долг о. наследников. Не иметь определённых намерений о. кого-л.

нареч. и предлог.

1. нареч.

Более или менее, до некоторой степени.

[Лиза] выпрыгнула [из шарабана]. Прыжок был относительно счастливый, - она могла зацепиться за колесо. Л. Толстой, Дьявол.

Море было относительно спокойно. Белесая полоса тумана закрывала горизонт. Чаковский, У нас уже утро.

2. предлог с род. п. По отношению к кому-, чему-л., в отношении кого-, чего-л.

Симметрия геометрических фигур относительно оси.

◊

[Гурмыжская:] Я должна исполнить долг свой относительно наследников. А. Островский, лес.

Относительно ее я не имел никаких определенных намерений и ни о чем не мечтал. Чехов, Страх.

относи́тельно, нареч. и предлог

относительно

нареч, кол-во синонимов: 14

сравнительно, более или менее

сравнительно, условно, насчет, более или менее, релятивно, про, по поводу, касательно

неизм.

сравнительно

в сравнении с чем-либо)

соотношение

▲ в отношении

↑ какой-л. объект

относительно - в отношении кого - чего (обязанности # детей).

в отношении того, что.

в деле чего.

в. во. в деле (успехи в деле укрепления мира).

относительно того .

о (забота о детях). об (удариться обо что).

про (думать # это).

по (скучать по родине).

по отношению к.

по поводу чего (пройтись по этому поводу).

по поводу того . по тому поводу, что.

по случаю (# праздника).

по части чего (# торговли).

вокруг чего (# этого идет много споров).

к чему (понятно # он клонит).

касательно чего. насчет чего.

дело касается кого - чего.

что касается кого - чего, то . .

что до (# меня, то я согласен).

на счет (принимать на свой счет. на этот счет).

по адресу.

дело с чем. обстановка [ситуация] с чем.

для кого - чего (вредно # здоровья. время # меня дорого).

к (способность к абстракции).

по отношению к [ко] кому - чему.

перед (преклоняться # героями).

насчет того. насчет того, что.

↓ любой, быть темой, отрицательный сигнал, физика, репутация

см. уточнение - пояснение, соответствие (между)

относи́тельн/о.

относи́тельно н; предл.

Составить слова из слова относительно

прил., кол-во синонимов: 2

Составить слова из слова относительно близкий по родству

прил., кол-во синонимов: 1

Составить слова из слова относительно большой

относи/тельно бы/стрый

Составить слова из слова относительно быстрый

относи/тельно вла/жный

прил., кол-во синонимов: 1

Составить слова из слова относительно влажный

прил., кол-во синонимов: 1

Составить слова из слова относительно высокий

прил., кол-во синонимов: 1

Составить слова из слова относительно густозасёленный

прил., кол-во синонимов: 1

Составить слова из слова относительно густозаселенный

прил., кол-во синонимов: 1

Составить слова из слова относительно жёсткий

прил., кол-во синонимов: 2

Составить слова из слова относительно жесткий

прил., кол-во синонимов: 1

Составить слова из слова относительно завершённый

прил., кол-во синонимов: 1

Составить слова из слова относительно завершенный

относи/тельно кру/пный

Составить слова из слова относительно крупный

прил., кол-во синонимов: 1

Составить слова из слова относительно мягкий

относи/тельно небольшо/й

Составить слова из слова относительно небольшой

относи/тельно незави/симый

Составить слова из слова относительно независимый

прил., кол-во синонимов: 1

Составить слова из слова относительно неизменённый

прил., кол-во синонимов: 1

Составить слова из слова относительно неизмененный

Я осмеливаюсь попросить вас относительно одного очень тонкого обстоятельства

Гоголь. Ревизор. 4, 7. Добчинский.

Ср. Тонкий намек на толстые обстоятельства.

Составить слова из слова относительно одного очень тонкого обстоятельства

относи/тельно постоя/нный

Составить слова из слова относительно постоянный

относи/тельно ро/вный

Составить слова из слова относительно ровный

относи/тельно свобо/дный

Составить слова из слова относительно свободный

относи/тельно си/льный

Составить слова из слова относительно сильный

относи/тельно стаби/льный

Составить слова из слова относительно стабильный

прил., кол-во синонимов: 1

Составить слова из слова относительно тёплый

прил., кол-во синонимов: 1

Составить слова из слова относительно теплый

союз

1. Употребляется при присоединении придаточной части сложноподчиненного предложения (в которой содержится описательная передача чьей-либо речи, мысли, состояния), соответствуя по значению сл.: насчёт того что; по поводу того что.

2. Употребляется при присоединении придаточной части сложноподчиненного предложения (в которой говорится о действии, являющемся объектом высказывания, который необходимо выделить), соответствуя по значению сл.: насчёт того что; по поводу того что.

Составить слова из слова относительно того что

прил., кол-во синонимов: 1

Составить слова из слова относительно удалённый

прил., кол-во синонимов: 1

Составить слова из слова относительно удаленный

относи/тельно уме/ренный

Составить слова из слова относительно умеренный

относи/тельно-безли/чный

Составить слова из слова относительно-безличный

То же, что косвенно-вопросительное подчинение.

Составить слова из слова относительно-вопросительное подчинение

относи/тельно-вопроси/тельный

прил., кол-во синонимов: 1

Составить слова из слова относительно-вопросительный

относи/тельно-материа/льный

Составить слова из слова относительно-материальный

относи/тельно-притяжа/тельный

Составить слова из слова относительно-притяжательный

Глагольная форма времени, определяющаяся не соотношением с моментом речи, а соотношением с другой временной формой (в предложении. Секретарь сказал, что директор находится у себя в кабинете (форма настоящего времени находится указывает на совпадение времени действия не с моментом речи, а с временем действия, выраженного глаголом сказал). ср.: абсолютное время.

Составить слова из слова относительное время

Относи́тельное движе́ние - движение точки (или тела) по отношению к системе отсчёта, перемещающейся относительно некоторой другой, основной, системы отсчёта, условно называемой неподвижной.

* * *

ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ - ОТНОСИ́ТЕЛЬНОЕ ДВИЖЕ́НИЕ, движение точки (или тела) по отношению к системе отсчета, перемещающейся относительно некоторой другой, основной, системы отсчета, условно называемой неподвижной.

ОТНОСИТЕЛЬНОЕ движение - движение точки (или тела) по отношению к системе отсчета, перемещающейся относительно некоторой другой, основной, системы отсчета, условно называемой неподвижной.

Составить слова из слова относительное движение

ОТНОСИТЕЛЬНОЕ ОТВЕРСТИЕ - ОТНОСИ́ТЕЛЬНОЕ ОТВЕ́РСТИЕ, отношение диаметра действующего отверстия объектива к его фокусному расстоянию. Квадрат относительного отверстия определяет освещенность в плоскости изображения и часто называется геометрической светосилой объектива.

ОТНОСИТЕЛЬНОЕ ОТВЕРСТИЕ - отношение диаметра действующего отверстия объектива к его фокусному расстоянию. Квадрат относительного отверстия определяет освещенность в плоскости изображения и часто называется геометрической светосилой объектива.

Составить слова из слова относительное отверстие

Относи́тельное отве́рстие объекти́ва - светотехническая характеристика объектива, определяющая освещённость формируемого им изображения. Геометрическое относительное отверстие объектива - отношение диаметра входного зрачка (отверстия) объектива к его заднему фокусному расстоянию. Квадрат относительного отверстия объектива определяет освещённость в плоскости изображения и часто называется геометрической светосилой объектива.

Составить слова из слова относительное отверстие объектива

относительное подчинение - см. подчинение относительное (в статье подчинение предложений),

Составить слова из слова относительное подчинение

То же, что союзное слово.

Составить слова из слова относительное слово

Относи́тельности при́нцип - фундаментальный физический закон, согласно которому любой процесс протекает одинаково в изолированной материальной системе, находящейся в состоянии покоя, и в такой же системе в состоянии равномерного прямолинейного движения. Состояния движения или покоя определяются по отношению к произвольно выбранной инерциальной системе отсчёта. Относительности принцип лежит в основе специальной теории относительности Эйнштейна.

* * *

ОТНОСИТЕЛЬНОСТИ ПРИНЦИП - ОТНОСИ́ТЕЛЬНОСТИ ПРИ́НЦИП, фундаментальный физический закон, согласно которому любой процесс протекает одинаково в изолированной материальной системе, находящейся в состоянии покоя, и в такой же системе в состоянии равномерного прямолинейного движения. Состояния движения или покоя определяются по отношению к произвольно выбранной инерциальной системе отсчета. Принцип относительности лежит в основе специальной теории относительности Эйнштейна.

ОТНОСИТЕЛЬНОСТИ Принцип - фундаментальный физический закон, согласно которому любой процесс протекает одинаково в изолированной материальной системе, находящейся в состоянии покоя, и в такой же системе в состоянии равномерного прямолинейного движения. Состояния движения или покоя определяются по отношению к произвольно выбранной инерциальной системе отсчета. Принцип относительности лежит в основе специальной теории относительности Эйнштейна.

ОТНОСИТЕЛЬНОСТИ ПРИНЦИП, согласно которому во всех инерциальных системах отсчёта физические явления протекают одинаково; впервые высказан А. Пуанкаре в 1895, окончательно сформулирован А. Эйнштейном в 1905.

Составить слова из слова относительности принцип

Относи́тельности тео́рия - Эйнштейна, физическая теория, рассматривающая пространственно-временные свойства физических процессов. Так как закономерности, устанавливаемые теорией относительности, - общие для всех физических процессов, то обычно о них говорят просто как о свойствах пространства-времени. Эти свойства зависят от полей тяготения в данной области пространства-времени. Теория, описывающая свойства пространства-времени в приближении, когда полями тяготения можно пренебречь, называется специальной или частной теорией относительности, или просто теория относительности (создана А. Эйнштейном в 1905). Свойства пространства-времени при наличии полей тяготения исследуются в общей теории относительности, называемой также теорией тяготения Эйнштейна (создана в 1915-16; см. Тяготение). Физические явления, описываемые теорией относительности, называются релятивистскими и проявляются при скоростях v движения тел, близких к скорости света в вакууме с.

В основе теории относительности лежат 2 положения: 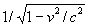m тела растёт с увеличением его скорости v по формуле 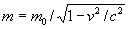, где m₀ - масса покоя тела. Полная энергия движущегося тела определяется соотношением Эйнштейна Е = mc²; покоящееся тело обладает энергией Е = m₀с². Все эти закономерности теории относительности надёжно подтверждены на опыте. Теория относительности выявила ограниченность представлений классической физики об «абсолютных» пространстве и времени, неправомерность их обособления от движущейся материи; она даёт более точное, по сравнению с классической механикой, отображение объективных процессов реальной действительности.

* * *

ОТНОСИТЕЛЬНОСТИ ТЕОРИЯ - ОТНОСИ́ТЕЛЬНОСТИ ТЕО́РИЯ Эйнштейна, физическая теория, рассматривающая пространственно-временные свойства физических процессов. Т. к. закономерности, устанавливаемые теорией относительности, - общие для всех физических процессов, то обычно о них говорят просто как о свойствах пространства-времени. Эти свойства зависят от полей тяготения в данной области пространства-времени. Теория, описывающая свойства пространства-времени в приближении, когда полями тяготения можно пренебречь, называется специальной или частной теорией относительности, или просто теорией относительности (создана А. Эйнштейном (см. ЭЙНШТЕЙН Альберт)в 1905). Свойства пространства-времени при наличии полей тяготения исследуются в общей теории относительности, называемой также теорией тяготения Эйнштейна (создана в 1915-16; см. Тяготение (см. ТЯГОТЕНИЕ)). Физические явления, описываемые теорией относительности, называются релятивистскими и проявляются при скоростях v движения тел, близких к скорости света в вакууме с.

В основе теории относительности лежат 2 положения: относительности принцип (см. ОТНОСИТЕЛЬНОСТИ ПРИНЦИП), означающий равноправие всех инерциальных систем отсчета (см. ИНЕРЦИАЛЬНАЯ СИСТЕМА ОТСЧЕТА)(и. с. о.), и постоянство скорости света в вакууме, ее независимость от скорости движения источника света. Эти 2 постулата определяют формулы перехода от одной инерциальной системы отсчета к другой - преобразования Лоренца, для которых характерно, что при таких переходах изменяются не только пространственные координаты, но и моменты времени (относительность времени). Из преобразований Лоренца получаются основные эффекты специальной теории относительности: существование предельной скорости передачи любых взаимодействий - максимальной скорости, до которой можно ускорить тело, совпадающей со скоростью света в вакууме; относительность одновременности (события, одновременные в одной инерциальной системе отсчета, в общем случае не одновременны в другой); замедление течения времени в быстро движущемся теле (физические процессы в теле, движущемся со скоростью v относительно некоторой инерциальной системы отсчета, протекают в раз медленнее, чем в данной инерциальной системе отсчета) и сокращение продольных - в направлении движения - размеров тел (во столько же раз) и др. Масса m тела растет с увеличением его скорости v по формуле , где m₀- масса покоя (см. МАССА ПОКОЯ)тела. Полная энергия движущегося тела определяется соотношением Эйнштейна E=mc²; покоящееся тело обладает энергией E=m₀c². Все эти закономерности теории относительности надежно подтверждены на опыте. Теория относительности выявила ограниченность представлений классической физики об «абсолютных» пространстве и времени, неправомерность их обособления от движущейся материи; она дает более точное, по сравнению с классической механикой, отображение объективных процессов реальной действительности.

* * *

ОТНОСИ́ТЕЛЬНОСТИ ТЕО́РИЯ - физическая теория пространства и времени. В частной (специальной) теории относительности рассматриваются только инерциальные системы отсчета (см. ИНЕРЦИАЛЬНАЯ СИСТЕМА ОТСЧЕТА).

Относительность движения по Галилею

Впервые положение об относительности механического движения было высказано в 1638 одним из основоположников современного естествознания Галилео Галилеем (см. ГАЛИЛЕЙ Галилео) в его труде «Диалог о двух основных системах мира - птоломеевой и коперниковой». Там же сформулирован один из фундаментальных принципов физики - принцип относительности. Галилей использовал наглядный и образный метод изложения. Он писал, что находясь «в помещении под палубой корабля» и проводя опыты и наблюдения над всем, что там происходит, нельзя определить, покоится ли корабль, или же он движется «без толчков», то есть равномерно и прямолинейно. При этом подчеркивались два положения, составляющие суть принципа относительности:

1) движение относительно: по отношению к наблюдателю «в помещении под палубой» и к тому, кто смотрит с берега, движение выглядит по-разному;

2) физические законы, управляющие движением тел в этом помещении, не зависят от того, как движется корабль (если только это движение равномерно). Иначе говоря, никакие опыты в «закрытой кабине» не позволяют определить, покоится кабина или движется равномерно и прямолинейно.

Таким образом, Галилей сделал вывод, что механическое движение относительно, а законы, которые его определяют, абсолютны, то есть безотносительны. Эти положения коренным образом отличались от общепринятых в то время представлений Аристотеля (см. АРИСТОТЕЛЬ) о существовании «абсолютного покоя» и «абсолютного движения».

Принцип относительности и законы Ньютона

Принцип относительности Галилея органически вошел в созданную И. Ньютоном (см. НЬЮТОН Исаак) классическую механику. Ее основу составляют три «аксиомы» - три знаменитых закона Ньютона. Уже первый из них, гласящий: «Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не принуждается приложенными силами изменить это состояние», говорит об относительности движения и одновременно указывает на существование систем отсчета (они были названы инерциальными), в которых тела, не испытывающие внешних воздействий, движутся «по инерции», не ускоряясь и не замедляясь. Именно такие инерциальные системы имеются ввиду и при формулировке двух остальных законов Ньютона. При переходе из одной инерциальной системы в другую меняются многие величины, характеризующие движение тел, например, их скорости или формы траектории движения, но законы движения, то есть соотношения, связывающие эти величины, остаются постоянными.

Преобразования Галилея

Чтобы описывать механические движения, то есть изменение положения тел в пространстве, Ньютон четко сформулировал представления о пространстве и времени. Пространство мыслилось как некий «фон», на котором развертывается движение материальных точек. Их положение можно определять, например, с помощью декартовых координат x, у, z, зависящих от времени t. При переходе из одной инерциальной системы отсчета К в другую К", движущуюся по отношению к первой вдоль оси x со скоростью v, координаты преобразуются: x"=x-vt, y"=у, z"=z, а время остается неизменным: t"=t. Таким образом принимается, что время абсолютно. Эти формулы получили название преобразований Галилея.

По Ньютону, пространство выступает как некая координатная сетка, на которую не влияет материя и ее движение. Время в такой «геометрической» картине мира как бы отсчитывается некими абсолютными часами, ход которых ничто не может ни ускорить, ни замедлить.

Принцип относительности в электродинамике

Принцип относительности Галилея более трехсот лет относили только к механике, хотя в первой четверти 19 в., прежде всего благодаря трудам М. Фарадея (см. ФАРАДЕЙ Майкл), возникла теория электромагнитного поля, получившая затем дальнейшее развитие и математическую формулировку в работах Дж. К. Максвелла (см. МАКСВЕЛЛ Джеймс Клерк). Но перенос принципа относительности на электродинамику представлялся невозможным, так как считалось, что все пространство заполнено особой средой - эфиром, натяжения в котором и истолковывались как напряженности электрического и магнитного полей. При этом эфир не влиял на механические движения тел, так что в механике он «не чувствовался», но на электромагнитных процессах движение относительно эфира («эфирный ветер») должно было сказываться. В результате находящийся в закрытой кабине экспериментатор при помощи наблюдения над такими процессами мог, казалось, определить, находится ли его кабина в движении (абсолютном!), или же она покоится. В частности, ученые полагали, что «эфирный ветер» должен влиять на распространение света. Попытки обнаружить «эфирный ветер», однако, не увенчались успехом, и концепция механического эфира была отвергнута, благодаря чему принцип относительности как бы родился заново, но уже как универсальный, справедливый не только в механике, но и в электродинамике, и других областях физики.

Преобразования Лоренца

Подобно тому, как математической формулировкой законов механики являются уравнения Ньютона, уравнения Максвелла являются количественным представлением законов электродинамики. Вид этих уравнений также должен оставаться неизменным при переходе из одной инерциальной системы отсчета в другую. Чтобы удовлетворить этому условию, необходимо заменить преобразования Галилея иными: x"= g (x-vt); y"=y; z"=z; t"= g (t-vx/c²), где g = (1-v²/c²)^-1/2, а с- скорость света в вакууме. Последние преобразования, установленные Х. Лоренцем (см. ЛОРЕНЦ Хендрик Антон)в 1895 и носящие его имя, являются основой специальной (или частной) теории относительности. При v

ОТНОСИТЕЛЬНОСТИ Теория - физическая Теория пространства и времени. В частной (специальной) теории относительности рассматриваются только инерциальные системы отсчета. Относительность движения по ГалилеюВпервые положение об относительности механического движения было высказано в 1638 одним из основоположников современного естествознания Галилео Галилеем в его труде "Диалог о двух основных системах мира - птоломеевой и коперниковой". Там же сформулирован один из фундаментальных принципов физики - принцип относительности. Галилей использовал наглядный и образный метод изложения. Он писал - что находясь "в помещении под палубой корабля" и проводя опыты и наблюдения над всем, что там происходит, нельзя определить, покоится ли корабль, или же он движется "без толчков", то есть равномерно и прямолинейно. При этом подчеркивались два положения, составляющие суть принципа относительности: 1) движение относительно: по отношению к наблюдателю "в помещении под палубой" и к тому, кто смотрит с берега, движение выглядит по-разному;

2) физические законы, управляющие движением тел в этом помещении, не зависят от того, как движется корабль (если только это движение равномерно). Иначе говоря, никакие опыты в "закрытой кабине" не позволяют определить, покоится кабина или движется равномерно и прямолинейно.Таким образом, Галилей сделал вывод, что механическое движение относительно, а законы, которые его определяют, абсолютны, то есть безотносительны. Эти положения коренным образом отличались от общепринятых в то Время представлений Аристотеля о существовании "абсолютного покоя" и "абсолютного движения".принцип относительности и законы НьютонаПринцип относительности Галилея органически вошел в созданную И.

Ньютоном классическую механику. Ее основу составляют три "аксиомы" - три знаменитых закона Ньютона. Уже первый из них, гласящий: "Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не принуждается приложенными силами изменить это состояние", говорит об относительности движения и одновременно указывает на существование систем отсчета (они были названы инерциальными), в которых тела, не испытывающие внешних воздействий, движутся "по инерции", не ускоряясь и не замедляясь. Именно такие инерциальные системы имеются ввиду и при формулировке двух остальных законов Ньютона. При переходе из одной инерциальной системы в другую меняются многие величины, характеризующие движение тел, например, их скорости или формы траектории движения, но законы движения, то есть соотношения, связывающие эти величины, остаются постоянными. Преобразования ГалилеяЧтобы описывать механические движения, то есть изменение положения тел в пространстве, Ньютон четко сформулировал представления о пространстве и времени. пространство мыслилось как некий "фон", на котором развертывается движение материальных точек. Их положение можно определять, например, с помощью декартовых координат x, у, z, зависящих от времени t. При переходе из одной инерциальной системы отсчета К в другую К , движущуюся по отношению к первой вдоль оси x со скоростью v, координаты преобразуются: x =x-vt, y =у, z =z, а Время остается неизменным: t =t. Таким образом принимается, что Время абсолютно. Эти формулы получили название преобразований Галилея. По Ньютону, пространство выступает как некая координатная сетка, на которую не влияет материя и ее движение. Время в такой "геометрической" картине мира как бы отсчитывается некими абсолютными часами, ход которых ничто не может ни ускорить, ни замедлить. принцип относительности в электродинамикеПринцип относительности Галилея более трехсот лет относили только к механике, хотя в первой четверти 19 в., прежде всего благодаря трудам М. Фарадея, возникла Теория электромагнитного поля, получившая затем дальнейшее развитие и математическую формулировку в работах Дж. К. Максвелла. Но перенос принципа относительности на электродинамику представлялся невозможным, так как считалось, что все пространство заполнено особой средой - эфиром, натяжения в котором и истолковывались как напряженности электрического и магнитного полей. При этом эфир не влиял на механические движения тел, так что в механике он "не чувствовался", но на электромагнитных процессах движение относительно эфира ("эфирный ветер") должно было сказываться. В результате находящийся в закрытой кабине экспериментатор при помощи наблюдения над такими процессами мог, казалось, определить, находится ли его кабина в движении (абсолютном!), или же она покоится. В частности, ученые полагали, что "эфирный ветер" должен влиять на распространение света. Попытки обнаружить "эфирный ветер", однако, не увенчались успехом, и концепция механического эфира была отвергнута, благодаря чему принцип относительности как бы родился заново, но уже как универсальный, справедливый не только в механике, но и в электродинамике, и других областях физики. Преобразования ЛоренцаПодобно тому, как математической формулировкой законов механики являются уравнения Ньютона, уравнения Максвелла являются количественным представлением законов электродинамики. вид этих уравнений также должен оставаться неизменным при переходе из одной инерциальной системы отсчета в другую. Чтобы удовлетворить этому условию, необходимо заменить преобразования Галилея иными: x = ? (x-vt); y =y; z =z; t = ? (t-vx/c2), где ? = (1-v2/c2)-1/2, а с - скорость света в вакууме. Последние преобразования, установленные Х. Лоренцем в 1895 и носящие его имя, являются основой специальной (или частной) теории относительности. При v""c они переходят в преобразования Галилея, но если v близко к c, то проявляются существенные отличия от картины пространства - времени, которую принято называть нерелятивистской. Прежде всего, обнаруживается несостоятельность привычных интуитивных представлений о времени, выясняется, что события, которые происходят одновременно в одной системе отсчета, перестают быть одновременными в другой. Меняется и закон преобразования скоростей. Преобразование физических величин в релятивистской теорииВ релятивистской теории пространственные расстояния и промежутки времени не остаются неизменными при переходе из одной системы отсчета в другую, движущуюся относительно первой со скоростью v. Длины сокращаются (в направлении движения) в 1/? раз, и в такое же число раз "растягиваются" промежутки времени. Относительность одновременности - основная принципиально новая черта современной частной теории относительности. Релятивистское обобщение законов механикиРешающий шаг в создании специальной теории относительности был сделан А. Эйнштейном в 1905. Исходя из невозможности обнаружить абсолютное движение, Эйнштейн сделал вывод о равноправии всех инерциальных систем отсчета. Он сформулировал два важнейших постулата, делавших излишней гипотезу о существовании эфира, которые составили основу обобщенного принципа относительности: 1) все законы физики одинаково применимы в любой инерциальной системе отчета и не должны меняться при преобразованиях Лоренца;

2) свет всегда распространяется в свободном пространстве с одной и той же скоростью, независимо от движения источника. Требование, чтобы вид основных уравнений физики был одинаков во всех инерциальных системах отсчета, применительно к уравнениям классической механики приводит к необходимости некоторой их модификации, сводящейся к замене массы тела mо (так называемой массы покоя) выражением m = ?mо, причем m неограниченно возрастает по мере приближения v к c. Поскольку масса является мерой инерции, последнее утверждение означает, что даже непрерывно подталкивая тело (частицу), невозможно сообщить ему (ей) скорость, большую или равную c. Из уравнений релятивистской механики (как и механики Ньютона) вытекает закон сохранения энергии, для которого получается новое выражение: E=mc2 . Это - знаменитое соотношение Эйнштейна, связывающее массу тела и его энергию. Иногда это соотношение ошибочно истолковывают как указание на возможность взаимных превращений массы и энергии. В действительности же оно означает лишь то, что масса всегда пропорциональна энергии. В частности, наличие у покоящейся частицы массы говорит и о наличии у нее энергии (энергии покоя), что не играет роли в классической механике, но приобретает принципиальное значение при рассмотрении процессов, в которых число и сорт частиц может изменяться и поэтому энергия покоя может переходить в другие формы. В атомных ядрах энергия притяжения частиц приводит к тому, что общая масса ядра оказывается меньше суммы масс отдельных частиц (дефект массы). Установление этого факта явилось одним из важнейших шагов к возникновению ядерной энергетики, так как позволило оценить ту значительную энергию, которая должна высвобождаться при делении тяжелых и слиянии легких ядер.Представления о пространстве и времени составляют основу физического миропонимания, что уже само по себе определяет значение теории относительности. Особенно велика ее роль в физике ядра и элементарных частиц, в том числе и для расчетов гигантских установок, которые предназначены для потоков очень быстрых частиц, необходимых для экспериментов, позволяющих продвинуться в изучении строения материи.Литература:Вавилов С. И. Экспериментальные основания теории относительности. М.; Л., 1928.Борн М. Эйнштейновская Теория относительности. 11 изд. М., 1972.Логунов А. А. Основы теории относительности. М., 1982.Паули В. Теория относительности. 11 изд. М., 1983.В. И. Григорьев ОТНОШЕНИЕ - частное от деления одной величины на другую.

ОТНОСИТЕЛЬНОСТИ ТЕОРИЯ, физическая теория, рассматривающая пространственно-временные свойства физических

процессов. Так как закономерности, устанавливаемые относительности теорией, - общие для всех физических процессов,

то обычно о них говорят просто как о свойствах пространства-времени. Теория, описывающая свойства пространства-времени

в приближении, когда тяготением можно пренебречь, называется специальной (частной) относительности теорией, или

просто относительности теорией (создана А. Эйнштейном в 1905). свойства пространства-времени при наличии полей

тяготения исследуются в общей относительности теории, называемой также теорией тяготения (Эйнштейн, 1915 - 16).

В основе относительности теории лежат 2 положения:

относительности принцип

и независимость скорости света от движения системы отсчёта [во всех инерциальных системах отсчёта (ИСО)

скорость света постоянна и равна c].

Эти два постулата определяют формулы перехода от одной ИСО к другой ИСО - преобразования Лоренца, при которых

изменяются не только пространственные координаты, но и моменты времени (относительность времени). Из преобразований

Лоренца вытекают основные физические следствия (называемые иногда релятивистскими эффектами): существование

предельной скорости передачи любых взаимодействий; относительность одновременности (события, одновременные в одной

ИСО, в общем случае неодновременны в другой); замедление течения времени в быстродвижущемся теле

[при наблюдении из

некоторой ИСО физические процессы в теле, движущемся

со скоростью v относительно этой ИСО, протекают в

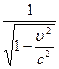
 раз медленнее, чем в теле, неподвижном в данной ИСО] и сокращение продольных - в направлении движения - размеров тел (во столько же раз) и др. Согласно относительности теории, не только кинематические (длина, время), но и динамические физические величины (импульс, энергия и др.) зависят от состояния движения тела (а следовательно, и от ИСО). Относительности теория выявила ограниченность представлений классической физики об "абсолютных" пространстве и времени; она даёт более точное, по сравнению с классической механикой, отображение реальных процессов. Относительности теория получила надёжное экспериментальное подтверждение, в частности, в опытах по измерению времени жизни нестабильных элементарных частиц, а также при работе с пучками заряженных частиц в ускорителях, электронно-лучевых трубках, электронных микроскопах и др.

Составить слова из слова относительности теория

ОТНОСИТЕЛЬНОСТИ Теория Эйнштейна - физическая Теория, рассматривающая пространственно-временные свойства физических процессов. Т. к. закономерности, устанавливаемые теорией относительности, - общие для всех физических процессов, то обычно о них говорят просто как о свойствах пространства-времени. Эти свойства зависят от полей тяготения в данной области пространства-времени. Теория, описывающая свойства пространства-времени в приближении, когда полями тяготения можно пренебречь, называется специальной или частной теорией относительности, или просто теорией относительности (создана А. Эйнштейном в 1905). Свойства пространства-времени при наличии полей тяготения исследуются в общей теории относительности, называемой также теорией тяготения Эйнштейна (создана в 1915-16; см.

Тяготение). Физические явления, описываемые теорией относительности, называются релятивистскими и проявляются при скоростях v движения тел, близких к скорости света в вакууме с. В основе теории относительности лежат 2 положения: относительности принцип, означающий равноправие всех инерциальных систем отсчета (и. с. о.), и постоянство скорости света в вакууме, ее независимость от скорости движения источника света. Эти 2 постулата определяют формулы перехода от одной инерциальной системы отсчета к другой - преобразования Лоренца, для которых характерно, что при таких переходах изменяются не только пространственные координаты, но и моменты времени (относительность времени). Из преобразований Лоренца получаются основные эффекты специальной теории относительности: существование предельной скорости передачи любых взаимодействий - максимальной скорости, до которой можно ускорить тело, совпадающей со скоростью света в вакууме; относительность одновременности (события, одновременные в одной инерциальной системе отсчета, в общем случае не одновременны в другой); замедление течения времени в быстро движущемся теле (физические процессы в теле, движущемся со скоростью v относительно некоторой инерциальной системы отсчета, протекают в раз медленнее, чем в данной инерциальной системе отсчета) и сокращение продольных - в направлении движения - размеров тел (во столько же раз) и др. масса m тела растет с увеличением его скорости v по формуле , где m0 - масса покоя тела. Полная энергия движущегося тела определяется соотношением Эйнштейна E=mc2; покоящееся тело обладает энергией E=m0c2. Все эти закономерности теории относительности надежно подтверждены на опыте. Теория относительности выявила ограниченность представлений классической физики об "абсолютных" пространстве и времени, неправомерность их обособления от движущейся материи; она дает более точное, по сравнению с классической механикой, отображение объективных процессов реальной действительности.

Составить слова из слова относительности теория эйнштейна

ж.

отвлеч. сущ. по прил. относительный I 1., 2.

ОТНОСИ́ТЕЛЬНОСТЬ, относительности, мн. нет, жен. (книжн.). отвлеч. сущ. к относительный; значение чего-нибудь, обнаруживающееся только в сопоставлении с другим, условность. «…В каждой научной истине, несмотря на ее относительность, есть элемент абсолютной истины…» Ленин. Теория относительности (учение в физике).

ОТНОСИ́ТЕЛЬНЫЙ, -ая, -ое; -лен, -льна.

-и, ж.

Свойство по прил. относительный (во 2 знач.).

Материалистическая диалектика --- признает относительность всех наших знаний не в смысле отрицания объективной истины, а в смысле исторической условности пределов приближения наших знаний к этой истине. Ленин, Материализм и эмпириокритицизм.

◊

теория относительности

физическая теория, рассматривающая пространственно-временные свойства физических процессов.

Теории относительности образуют существенную часть теоретического базиса современной физики. Существуют две основные теории: частная (специальная) и общая. Обе были созданы А.Эйнштейном, частная - в 1905, общая - в 1915. В современной физике частная теория относительности (ТО) вместе с квантовой механикой (которая в окончательном виде была сформулирована к 1925) играет такую же роль, какую раньше играла механика Ньютона. Ньютоновская механика хорошо описывала поведение объектов средних размеров, движущихся со скоростями, намного меньшими скорости света, но не могла описать движение очень малых объектов, таких, как атомы и входящие в состав атомов частицы или же частицы, из которых состоят космические лучи. Эти несоответствия стали проявляться в начале 20 в., и средства их преодоления оказались поистине революционными: квантовая механика, рассматривающая поведение очень малых частиц, отвергла ньютоновский детерминизм, а частная теория относительности, применимая к быстро движущимся телам, отвергла ньютоновское представление об абсолютном времени. Ньютоновская механика по-прежнему применяется в практических расчетах и в тех разделах астрономии, где рассматриваемые объекты - планеты, самолеты, автомобили - достаточно велики и движутся со скоростью, намного меньшей скорости света. Но как частная ТО, так и квантовая механика очень важны для теоретического мышления физика, тем более что их правильность подтверждается многочисленными экспериментами. На этих теориях основывается почти вся современная ядерная физика.

См. также

АТОМ;

МЕХАНИКА;

КВАНТОВАЯ МЕХАНИКА. В то же время общая теория относительности (ОТО), несмотря на ее огромное теоретическое значение, имеет довольно узкую область практического применения. Это в основном теория тяготения и инерции, заменяющая ньютоновскую теорию тяготения в точных расчетах очень больших систем (планетарного масштаба и более).

Она позволяет в рамках физики и астрономии рассматривать структуру Вселенной как целого. ОТО включает в себя частную ТО как частный случай и потому пригодна для описания всех явлений, которые правильно описываются как теорией Ньютона, так и частной ТО. При этом все практические отличия ОТО связаны только с гравитационным полем. Истоки возникновения теории относительности коренятся в противоречии между ньютоновской механикой и электромагнитной теорией Дж.Максвелла, выявившемся в конце 19 в. Созданию частной ТО, разрешающей это противоречие, мы обязаны не только Эйнштейну, но также Г.Лоренцу и А.Пуанкаре. Именно Лоренц и Пуанкаре создали математический аппарат частной ТО. Благодаря Эйнштейну, глубоко постигшему ее физический смысл, частная ТО получила быстрое и всеобщее признание. Среди более поздних исследователей, внесших существенный вклад в развитие частной ТО, следует упомянуть Г.Минковского (1864-1909). Минковский развил концепцию четырехмерного пространственно-временнго континуума, в котором времення координата рассматривается как равноправная с пространственными координатами; он предложил также удобную геометрическую интерпретацию уравнений частной ТО. Заслуга создания ОТО принадлежит исключительно Эйнштейну. Он ввел в физику новый математический аппарат - тензорное исчисление, разработанное Г.Риччи и Т.Леви-Чивитой. В математическом отношении теория оказалась весьма сложной, практических выводов из нее было мало, а проверить их путем наблюдений было трудно. В отличие от частной ТО, которая теперь почти полностью исследована, ОТО еще далека от этого. ОТО стала популярной не только среди физиков, но и в широких слоях образованных людей, когда наблюдения за затмением Солнца в 1919 подтвердили ее предсказание, согласно которому свет от далеких звезд, проходящий вблизи Солнца, должен испытывать отклонение. На ОТО базировались многочисленные попытки создания единых теорий поля, охватывавших не только гравитационные, но также электромагнитные и прочие физические явления. Такие попытки, однако, имели мало успеха, а после смерти Эйнштейна, который и сам предпринял ряд таких попыток, активность в этом направлении снизилась. Физики, уверенные в возможности создания единых теорий, объясняющих все физические явления, полагают, что более перспективен синтез ОТО с квантовой теорией. Релятивистская квантовая теория, в некоторой мере объединившая частную ТО и квантовую теорию, добилась заметного успеха в подтверждении теории электрона П.Дирака (1928). И хотя разработка общей релятивистской квантовой теории еще далека от завершения, есть основание надеяться, что именно с ее развитием будут связаны дальнейшие успехи теоретической физики в целом.

ЧАСТНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ

Ньютоновская механика. Данная статья написана так, что ее можно читать, не имея специальной математической подготовки. Необходимо лишь некоторое знание ньютоновской теории, имеющей с частной ТО ряд общих понятий. Начнем этот раздел с их рассмотрения. Основные представления ньютоновской теории заключаются в следующем. Пространство и время рассматриваются как абсолютные и первичные. Абсолютное пространство однородно и изотропно. Это означает, что все его точки, как и все направления в нем, равноправны. Параллельные линии не сходятся и не расходятся, а это означает, что рассматривается евклидово пространство, свойства которого полностью описываются евклидовой геометрией. На поведение тел влияет лишь их относительное расположение, а следовательно, их абсолютное расположение в пространстве не играет никакой роли. Любым подходящим твердым телом определяется "система отсчета", а положение и движение других тел описываются относительно системы координат, связанной с этим выбранным телом. Если система отсчета покоится или находится в состоянии равномерного прямолинейного движения по отношению к абсолютному пространству, то она называется инерциальной, галилеевской или ньютоновской. В любой инерциальной системе отсчета законы механики имеют одну и ту же форму, в чем и выражается принцип относительности Галилея (галилеевская инвариантность). Согласно второму закону Ньютона, в любой инерциальной системе отсчета скорость изменения импульса любого тела пропорциональна приложенной к нему силе. Из принципа относительности Галилея следует, что путем одних лишь механических экспериментов невозможно установить, находится ли данное тело в состоянии покоя или равномерного прямолинейного движения по отношению к абсолютному пространству. Если же система отсчета движется ускоренно по отношению к абсолютному пространству, то для удовлетворения законов Ньютона нужно ввести фиктивные силы инерции, типичными примерами которых являются центробежная сила и сила Кориолиса. "Абсолютное, истинное, математическое время само по себе и по самой своей сущности, без всякого отношения к чему-либо внешнему, протекает равномерно", - писал Ньютон в Математических началах натуральной философии (Philosophiae naturalis principia mathematica, 1687). Оно одно и то же в любой системе отсчета. Это очень важно, поскольку, как будет показано далее, время существенным образом входит в законы движения.

Пространственно-временные диаграммы. Диаграммы хорошо дополняют уравнения при объяснении принципов теории относительности, равно как и ньютоновской механики. Более всего наглядны графики, показывающие, как положение объектов меняется со временемми диаграммами. На рис. 1,а представлена ньютоновская пространственно-времення диаграмма, соответствующая равномерному и прямолинейному движению частицы Q вдоль оси х некоторой системы отсчета, в которой частица Р покоится. Координата х откладывается вправо, а время t - вверх. (Координаты y и z пока несущественны.) Диаграмма дает положение частицы Q в любой момент t. Наклонная линия, которая представляет историю частицы Q, называется мировой линией частицы. Любой момент в истории частицы Q, т.е. точка на мировой линии, называется мировой точкой или событием. Вертикальная ось - это мировая линия точки Р, которая находится в состоянии покоя. При t = 0 частица Q проходит мимо P. Можно сказать, что эта диаграмма вычерчена в системе отсчета, связанной с точкой Р. Тонкие горизонтальные линии являются линиями постоянного времени t (на которых время одинаково во всех точках). Они соединяют мировые точки, в которых события происходят одновременно. На рис. 1,б показана та же пара точек, но в системе отсчета, связанной с точкой Q. Теперь движется точка P, но влево от Q, поскольку ранее точка Q относительно P двигалась вправо. На рис. 1,в, как и на рис. 1,а, показаны точки P и Q и, кроме того, точка R, которая в начальный момент совпадает с Р, а затем уходит влево с нарастающей скоростью. Далее она замедляет движение и возвращается к Р. Изменения скорости характеризуются наклоном мировой линии относительно вертикали: чем больше скорость, тем больше изменение х при данном изменении t и тем больше наклон мировой линии.

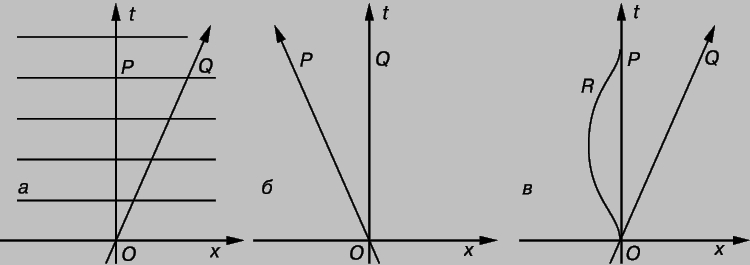
Рис. 1. ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ДИАГРАММЫ показывают, как изменяется положение тел во времени. Пространственная координата х (y и z для простоты не рассматриваются) увеличивается вправо от начала координат, а времення координата t - в направлении вверх. На рис. 1,а тело Q движется равномерно вправо относительно системы, в которой P покоится. Линия OQ - мировая линия тела Q, представляющая его историю. На рис. 1,б те же события представлены относительно системы, в которой тело Q покоится; тело P теперь движется влево относительно тела Q. На рис. 1,в происходит то же, что и на рис. 1,а, но добавлено тело R (при t = 0 оно находилось в начале координат вместе с телом P), которое движется с ускорением влево, замедляет движение, ускоренно движется вправо и встречается с P.

Наряду со временем на пространственно-временнй диаграмме можно представить и две пространственные координаты; гораздо труднее - три. На рис. 2 показана мировая линия планеты (в двух пространственных координатах), движущейся вокруг Солнца. Ее орбита приблизительно круговая, и потому мировая линия имеет вид винтовой линии. Расстояние по вертикали между двумя ее соседними витками равно времени одного полного оборота планеты вокруг Солнца.

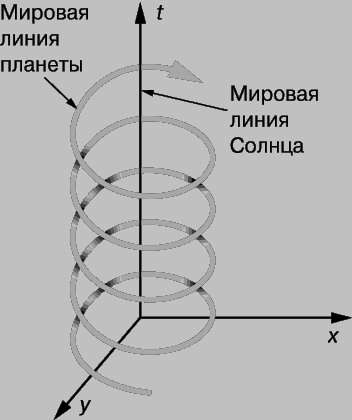
Рис. 2. МИРОВАЯ ЛИНИЯ ПЛАНЕТЫ относительно Солнца. Координаты x, y (z не показана) - пространственные, а t - времення. В координатах пространства-времени пространственная круговая орбита планеты становится винтовой линией. Поскольку пространственные координаты для каждого обращения планеты одни и те же, вертикальное расстояние между соседними витками винтовой линии есть время обращения планеты по орбите.

Распространение света. Как уже отмечалось, частная ТО возникла в результате противоречия между ньютоновской механикой и максвелловской электромагнитной теорией света. Согласно теории Максвелла, свет представляет собой электромагнитные колебания, которые в виде волны распространяются с определенной скоростью. Скорость света в вакууме, обозначаемая буквой с, составляет 299 792 458 м/с. Скорость света в материальных средах меньше, чем в вакууме. Во второй половине 19 в. было принято искать механические модели для всех физических явлений. Так, световые колебания рассматривались как колебания некоторой физической среды - "светоносного эфира". Предполагалось, что эфир неподвижен в абсолютном пространстве ньютоновской механики. Поэтому в принципе представлялось возможным в опытах со светом выявить движение Земли относительно эфира, т.е. ее абсолютное движение. При этом, если Земля движется в эфире со скоростью v, а свет - со скоростью с, то свет, движущийся в том же направлении, что и Земля, должен, согласно механике Ньютона, перемещаться относительно Земли со скоростью (с - v), а свет, движущийся в противоположном направлении, должен иметь относительно Земли скорость (с + v). Стало быть, если с помощью закрепленного на Земле прибора удастся измерить скорость света в двух противоположных направлениях, то можно найти как (с - v), так и (с + v), а следовательно, и вычислить v, т.е. скорость Земли относительно эфира или, что то же самое, относительно абсолютного пространства. Такие измерения невозможно выполнить посредством чисто механических экспериментов, поскольку для них справедлив принцип относительности Галилея, но распространение света в светоносном эфире с этим принципом не связано. Первая попытка измерения скорости движения Земли относительно светоносного эфира была сделана А.Майкельсоном в 1881. Этот "эфирный" эксперимент он впоследствии с большей точностью повторил вместе с Э.Морли, а потому теперь эти эксперименты называются опытами Майкельсона - Морли. Опыт основан на сравнении скорости света в двух взаимно перпендикулярных направлениях. Подробности опыта мы рассматривать не будем, но его результат имеет огромнейшее значение. Он показал, что скорость Земли относительно эфира в любой момент не превышает 1 км/с. Однако, как известно, скорость Земли на орбите составляет около 30 км/с, а поскольку направление ее движения изменяется на противоположное каждые 6 мес, то ее скорость в любом заданном направлении должна изменяться на протяжении полугода примерно на 60 км/с (рис. 3). Поэтому был сделан вывод, что скорость света относительно прибора практически не зависит от движения прибора относительно эфира - результат, который совершенно не согласуется с механикой Ньютона. Затем была выполнена серия еще более точных опытов, и результат неизменно оставался отрицательным.

См. также СВЕТ.

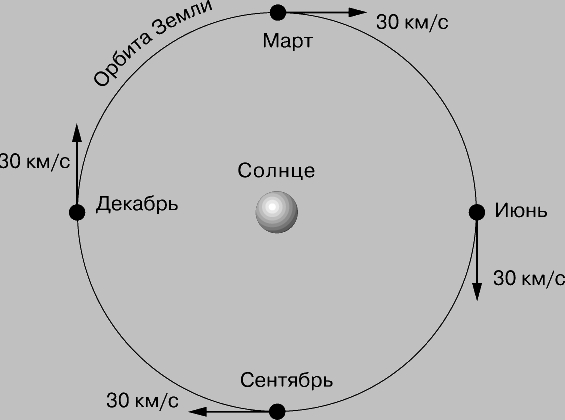
Рис. 3. СКОРОСТЬ ЗЕМЛИ, измеряемая в одном направлении, изменяется на протяжении полугода примерно на 60 км/с. Если пространство абсолютно и в нем существует неподвижный светоносный эфир, то в экспериментах, проведенных на Земле, скорость света должна была бы изменяться на 60 км/с. Эксперимент Майкельсона - Морли такого изменения не обнаружил, что поставило под вопрос существование эфира.

Это неожиданное открытие объяснялось по-разному. Предполагалось, что Земля должна каким-то образом увлекать за собой окружающий эфир. Однако гипотеза "увлекаемого эфира" противоречила некоторым астрономическим наблюдениям (таким, как звездная аберрация). Дж. Фитцджеральд (1851-1901) и независимо от него Г. Лоренц высказали предположение, что движение прибора (или любого другого предмета) в эфире должно вызывать сокращение его размеров на величину, необходимую для того, чтобы скомпенсировать ожидаемый эффект. Однако эта гипотеза о сокращении размеров, изначально базировавшаяся на ньютоновских представлениях, оказалась в противоречии с модифицированным опытом Майкельсона - Морли, выполненным в 1932 Р.Кеннеди и Э.Торндайком. В.Ритц выступил с утверждением, что скорость света в вакууме всегда должна быть равна с не относительно эфира, а относительно источника света, но это противоречило опытам Р.Томашека (выполненным с использованием солнечного света и света звезд в 1924 в духе опытов Майкельсона - Морли), а также астрономическим наблюдениям орбит двойных звезд.

Все разнообразие этих наблюдений можно свести к одному положению, с которым не согласуется ни одна из упомянутых гипотез: наблюдаемая скорость света, испускаемого движущимся в вакууме источником, не зависит от движения наблюдателя. Это положение явно противоречит ньютоновской механике.

Пространственно-временные диаграммы в частной ТО. Противоречие было разрешено частной ТО, основные положения которой следуют из эмпирического заключения об инвариантности скорости света, принципа относительности Галилея и модифицированного второго закона Ньютона. Должны быть также модифицированы и уравнения преобразований Галилея. Чтобы согласовать утверждение об инвариантности скорости света с классическими преобразованиями Галилея, последние нужно изменить так, чтобы скорость света во всех инерциальных системах отсчета была одной и той же. Пространственно-временне диаграммы, представленные на рис. 4, показывают, чту из этого следует. На них мы видим мировые линии двух наблюдателей P и Q, с каждым из этого следует. На них мы видим мировые линии двух наблюдателей P и Q, с каждым из которых связана инерциальная система отсчета. На верхних диаграммах покоится Р, а Q движется вправо со скоростью v. В момент, когда Q проходит мимо Р, там вспыхивает лампа и световые лучи L и R расходятся влево и вправо со скоростью с. Поскольку скорости в обоих направлениях равны, лучи наклонены по отношению к вертикали одинаково. На нижних диаграммах представлен случай, когда путем надлежащего преобразования был осуществлен переход к другой инерциальной системе отсчета, где Q покоится, а Р движется влево со скоростью v. Левая диаграмма соответствует механике Ньютона: лампа наблюдателя Р теперь движется вместе с ним со скоростью v и, следовательно, световой луч L, распространяющийся влево, имеет скорость (c + v), тогда как луч R, распространяющийся вправо, имеет скорость (с - v). Это различие представлено разным наклоном лучей.

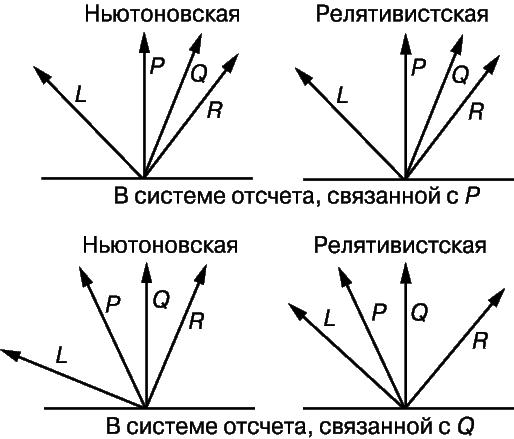
Рис. 4. ПРИНЦИП ИНВАРИАНТНОСТИ СКОРОСТИ СВЕТА есть основа теории относительности, тогда как в ньютоновской теории скорость света зависит от скорости наблюдателя. В момент прохождения наблюдателя Q мимо наблюдателя P последний включает лампу. Световые лучи L и R расходятся влево и вправо. Как ньютоновская, так и релятивистская диаграммы показывают, что в системе отсчета, связанной с P, L и R расходятся с равными скоростями. В системе же отсчета, связанной с Q, скорость луча L на ньютоновской диаграмме больше, чем луча R, тогда как на релятивистской диаграмме лучи L и R распространяются с одинаковыми скоростями. Для согласования ньютоновских и релятивистских результатов потребовались преобразования Лоренца. Как и на рис. 2, здесь изображены мировые линии, а не геометрические траектории.

К сожалению, приведенное рассуждение противоречит требованию постоянства скорости света с в любой инерциальной системе отсчета. Представленная же справа диаграмма - релятивистская - соответствует случаю, когда это требование выполняется. В новой системе отсчета скорости обоих световых лучей равны с. Поэтому пространство-время должно быть подвергнуто таким преобразованиям, чтобы скорость света осталась неизменной. Этому условию удовлетворяют преобразования Лоренца.

Концепция пространства-времени. То, каким образом пространственные координаты x, y, z и время t входят в уравнения преобразований Лоренца, навело Минковского на мысль, что пространство и время следует рассматривать не так, как в механике Ньютона с ее трехмерным евклидовым пространством и совершенно обособленной временнй координатой, а всегда вместе, в виде некой четырехмерной комбинации. Новая концепция оказалась очень плодотворной и благодаря наглядной геометрической интерпретации во многом способствовала развитию теории. (Такое пространство-время часто называют пространством Минковского.) Вместо того чтобы рассматривать физическую систему как совокупность частиц в пространстве, ее следует представить как совокупность мировых линий частиц в пространстве-времени, которая описывает полную историю системы. Как и евклидово пространство в механике Ньютона, пространство-время Минковского однородно, изотропно и обладает дополнительными свойствами симметрии, вытекающими из преобразований Лоренца.

Главные следствия частной ТО.

Многие результаты частной ТО вытекают из преобразований Лоренца. Ниже приводятся лишь сами результаты, а не их вывод.

Относительность времени (относительность одновременности). В теории относительности не существует абсолютного ньютоновского времени. В преобразованиях Галилея время остается без изменений. Из формул преобразований Лоренца следует, однако, что время в разных системах отсчета течет по-разному. На рис. 5 представлены две пространственно-временне диаграммы. На обеих отображены одни и те же события, но одна соответствует системе отсчета, связанной с Р, а другая - системе, связанной с Q и движущейся относительно Р. Таким образом, они согласуются с релятивистскими диаграммами рис. 4 (справа), но здесь вместо одной оси х имеются две - для P и Q. Оси и мировые точки D, E, F, G и Н изображены так, что их положения на обеих диаграммах согласуются с преобразованиями Лоренца. На рис. 5,а, в системе, где Р покоится, мировые точки E, F и G лежат на горизонтальной линии, а это означает, что все три представленных события происходят в одно время в разных местах (одно и то же t, но разные х). Событие D наступает раньше других, а событие Н - позже. На рис. 5,б, в системе, где Q покоится, мировые точки, соответствовавшие в предыдущем случае одновременным событиям (при одном и том же значении t), теперь соответствуют событиям, происходящим при разных значениях tў. Рассмотрим диаграмму. События E, F и G более не являются одновременными: сначала произойдет G, затем F и, наконец, E. Событие D по-прежнему произойдет раньше Е, но позжеF, хотя в предыдущем случае оно, как и следует из преобразований Лоренца, происходило раньше F. Аналогично ведут себя события H и G. Таким образом, относительна не только одновременность событий, но и порядок их наступления. Рассмотрим события D и E, а также события G и H. Каждая пара событий имеет на левой диаграмме одинаковую абсциссу х, указывающую на то, что пара событий происходила в одном и том же месте. Все эти события теперь будут происходить в разных местах (рис. 5,б ). Конечно, то же самое происходит и в ньютоновской теории. Упорядоченность событий от прошлого к будущему нарушается в ТО далеко не всегда. Некоторые события имеют вполне определенный порядок, вне зависимости от используемой для их описания системы отсчета. Например, опыт показывает, что события на мировой линии некоторого наблюдателя должны происходить в определенном порядке, и два наблюдателя всегда согласятся по поводу порядка событий, при которых они оба присутствовали.

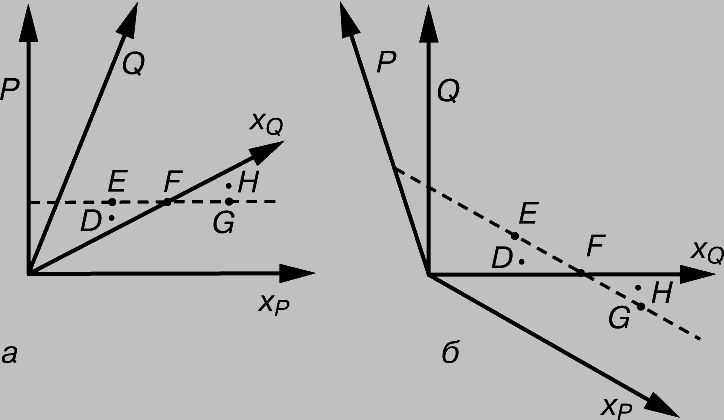
Рис. 5. ОТНОСИТЕЛЬНОСТЬ ОДНОВРЕМЕННОСТИ рушит представления о времени как не зависящем от движения в какой-либо системе отсчета. События, одновременные в одной системе отсчета, не являются таковыми в другой, и наоборот. В системе отсчета, связанной с P (в которой Q равномерно движется вправо от P), событие D происходит раньше одновременных событий E, F, G, а событие H - позже них. В системе отсчета, связанной с Q (в которой P движется равномерно влево от Q), события E, F, G более не являются одновременными; событие D происходит после F, а событие H - раньше F.

Рассмотрим это подробнее. Если (x1, y1, z1, t1) и (x2, y2, z2, t2) - пространственно-временне координаты двух событий, то выражение

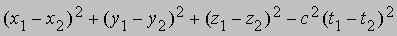
не меняет своего вида при преобразованиях Лоренца и, следовательно, имеет одно и то же определенное значение независимо от того, в какой системе отсчета ведутся измерения. Если для некоторых двух событий это выражение равно нулю или отрицательно, то, как можно показать, события должны происходить в определенном порядке, одинаковом для всех систем отсчета. Если же это выражение положительно, то порядок событий зависит от системы отсчета: в различных системах одно или другое событие произойдет раньше, причем есть и такая система, в которой оба они произойдут одновременно. На рис. 6 представлена пространственно-времення диаграмма истории световой вспышки, произошедшей в мировой точке O в момент t = 0. Спустя время t свет распространится на расстояние ct во всех направлениях и будет находиться на поверхности сферы радиусом ct. История этой сферы на диаграмме имеет вид конуса с вершиной в точке O. Этот конус (верхний на рис. 6) называется конусом будущего. События, свет от которых достигнет точки O в момент t = 0, образуют конус прошлого (нижний конус на рис. 6). Он выглядит точно так же, как конус будущего, но обращен назад. Вместе конусы прошлого и будущего образуют двойной конус с вершиной в пространственно-временнй точке O, называемый "световым конусом".

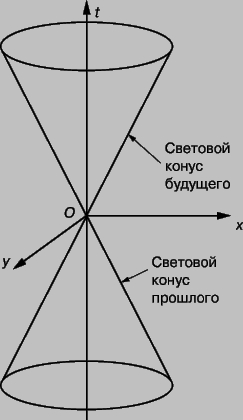
Рис. 6. СВЕТОВОЙ КОНУС на пространственно-временнй диаграмме иллюстрирует некоторые следствия теории относительности для понятия времени. В ньютоновской теории время абсолютно. В теории относительности время между событиями и их последовательность зависят от системы отсчета. Световой конус будущего, исходящий из точки O вверх (при фиксированном t - сфера, соответствующая распространению света во всех направлениях на расстояние ct, начавшемуся в момент t = 0, из точки О), представляет события, которые должны случиться после события O. Световой конус прошлого представляет события, которые должны произойти ранее O: он состоит из точек, откуда свет достигнет O в момент t = 0. Все точки вне двойного конуса представляют события, которые в зависимости от системы отсчета могут случиться как раньше, так и позже события O.

Любое событие, располагающееся внутри конуса будущего, всегда (во всех системах отсчета) происходит после события O. Поэтому событие O может, в принципе, быть его причиной. Любое событие, лежащее внутри конуса прошлого, всегда происходит до события O. Поэтому оно может, в принципе, быть причиной O. Любое событие, лежащее вне светового конуса, может происходить как до, так и после O, в зависимости от система отсчета. Поэтому между ним и событием O не может быть причинно-следственной связи. Сам световой конус не меняет формы при преобразованиях Лоренца, т.е. выглядит одинаково во всех системах отсчета, и это согласуется с опытным фактом, на котором основывается частная ТО, а именно, что скорость света в вакууме не зависит ни от движения источника, ни от движения наблюдателя.

Сокращение Фитцджеральда - Лоренца (лоренцево сокращение). Из преобразований Лоренца сразу же следует, что измеренная длина движущегося объекта отличается от его длины, измеренной, когда он покоится. Рассмотрим стержень, который покоится в некоторой системе отсчета, и пусть его длина, измеренная в этой системе, равна L. Если положение концов стержня измерить одновременно в системе отсчета, которая движется относительно первой со скоростью v (в направлении длины стержня), то выяснится, что расстояние между концами стержня равно уже не L, а L/g, где

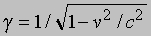
, а c - скорость света. Таким образом, вследствие движения измеренная длина стержня сокращается в g раз. Величина g очень близка к единице, если скорость стержня мала по сравнению со скоростью света, и резко возрастает, когда его скорость приближается к c. Этим без всяких дополнительных гипотез о поведении объектов относительно абсолютного пространства или о свойствах эфира объясняется отрицательный результат опыта Майкельсона - Морли. Лоренцево сокращение объясняется только относительным движением объектов. То же относится и ко всем другим вопросам, рассматриваемым в рамках частной ТО.

Замедление времени. Так называемое замедление времени или замедление хода движущихся часов, - явление, аналогичное рассмотренному выше сокращению длины. Оно состоит в изменении в g раз длительности измеряемых временных промежутков. Здесь есть два важных следствия, одно из которых имеет непосредственное приложение в физике. Рассмотрим, как и прежде, двух наблюдателей P и Q и два события D и E, например в истории Q. Предположим, что в системе отсчета, где Q покоится (система Q), событие E происходит t секундами позже события D. Тогда в системе, где покоится P (система P), эти два события происходят в точках, разделенных расстоянием vg t, а E происходит после D не через t, а через g t секунд. Поскольку всегда g > 1, время между двумя событиями, измеренное в систем

относи́тельность, -и

относи́тельность, относи́тельности, относи́тельностей, относи́тельностям, относи́тельностью, относи́тельностями, относи́тельностях

сущ., кол-во синонимов: 4

условность, релятивность (книжн.)

релятивность, релятивизм, условность

Syn: см. условность

относи́тельн/ость/.

относи́тельность ж 8a

- Литография голландского художника Эшера.

- Оценивание в сравнении с другими.

Составить слова из слова относительность

относительные местоимения - см. местоимения вопросительно-относительные (в статье местоимение),

Составить слова из слова относительные местоимения

Разряд прилагательных, которые называют признак через отношение к другому предмету или явлению: горное село, завтрашний день. Грамматическими показателями относительных прилагательных являются наличие полной склоняемой формы и отсутствие краткой формы.

относительные прилагательные - см. прилагательные относительные (в статье имя прилагательное).

Составить слова из слова относительные прилагательные

относительные синонимы - семантические конструкции, соотносимые по построению и совпадающие по значению.

Составить слова из слова относительные синонимы

I прил.

1. Устанавливаемый по сравнению, по сопоставлению с чем-либо другим.

Ant:

абсолютный

2. Изменяющийся в зависимости от окружающих условий; не безусловный, не абсолютный.

3. Ограниченный, умеренный, небольшой.

II прил.

Показывающий, выражающий отношения между главным и придаточным предложениями (в лингвистике).

ОТНОСИ́ТЕЛЬНЫЙ -ая, -ое; -лен, -льна, -льно.

1. Устанавливаемый по сравнению с чем-л. другим, верный только в определённых отношениях; сравнительный. Счастье - понятие о-ое. Яркость и цвет - характеристики весьма о-ые. Всё относительно на этом свете. О-ая влажность воздуха (по отношению к абсолютной влажности).

2. Некоторый, сравнительно небольшой, умеренный. О-ые успехи. Тишина была относительна. Находиться в относительной безопасности.

3. только полн. Грамм. Показывающий отношение к чему-л., между чем-л. О-ое местоимение. О-ое прилагательное. О-ое слово (местоимение).

◁ Относи́тельность, -и; ж. (1 зн.). О. знаний. О. истины. Теория относительности (устанавливающая общие закономерности протекания физических процессов во времени и пространстве).

ОТНОСИТЕЛЬНЫЙ, устанавливаемый в сравнении, в сопоставлении с чем-либо другим (например, относительная влажность); сравни Абсолютный.

Составить слова из слова относительный