м.
Специалист в области геометрии [геометрия I 1., 2.].
Á сущ см. Приложение II
Сведения о старой норме ударения:
Неудивительно, если вы произносите данное слово по-иному. Ударение на третьем слоге, соответствующее греческому языку-источнику, ср. γεωμέτρης, долгое время приводилось словарями как вариант нормы. Вы также можете попадать под влияние аналогии: геоме́трия - геоме́тр. Отличное от современной нормы ударение встречается у поэтов:
Скажи мне, чертежник пустыни,
Арабских песков геоме́тр,
Ужели безудержность линий
Сильнее, чем дующий ветр?
О. Э. Мандельштам, «Скажи мне, чертежник пустыни...»
геоме́тр, геоме́тры, геоме́тра, геоме́тров, геоме́тру, геоме́трам, геоме́тром, геоме́трами, геоме́тре, геоме́трах
- Математик с циркулем.
- И Евклид, и Лобачевский.
- Именно так древние греки называли просто землемера.
ГЕОМЕТРАЛЬНЫЙ ая, ое. géométral adj. <, лат. geometralis. Изображенный со всеми измерениями, но без перспективы. Михельсон 1877. Всякой архитектор делает планы и геометральные фасады. Баженов 119. План Геометральной, или по Руски плоскость земле мерная. Витр. (к). 14. - Лекс. Сл. 18: геометральный 1768.
Геометриза́ция месторожде́ния - комплекс работ по сбору, систематизации, математической обработке и графическому изображению данных о структурных и качественных особенностях месторождения полезного ископаемого.
* * *
ГЕОМЕТРИЗАЦИЯ МЕСТОРОЖДЕНИЯ - ГЕОМЕТРИЗА́ЦИЯ МЕСТОРОЖДЕ́НИЯ, комплекс работ по сбору, систематизации, математической обработке и графическому изображению данных о структурных и качественных особенностях месторождения полезного ископаемого (см. МЕСТОРОЖДЕНИЕ ПОЛЕЗНОГО ИСКОПАЕМОГО) .
ГЕОМЕТРИЗАЦИЯ МЕСТОРОЖДЕНИЯ - комплекс работ по сбору, систематизации, математической обработке и графическому изображению данных о структурных и качественных особенностях месторождения полезного ископаемого.
геометриза́ция недр
(см. геометрия) горн, составление маркшейдерских планов (см. маркшейдерия), характеризующих условия залегания, качество и структуру месторождения полезного ископаемого.
Геометрия - раздел математики, тесно связанный с понятием пространства; в зависимости от форм описания этого понятия возникают различные виды геометрии. Предполагается, что читатель, приступая к чтению этой статьи, обладает некоторыми представлениями об элементарной геометрии, а также о законах арифметики и алгебры.
См. также
Первый важный вопрос: как описать наше понятие пространства? В поисках ответа перед нами открывается несколько возможностей, но проще, а возможно, естественнее и полезнее воспользоваться для этого понятиями "точка" и "прямая". Оба они коренятся в процессе визуального восприятия. Точку можно мысленно представлять как "точку зрения", из которой ведется наблюдение, а прямую, определяемую двумя объектами, считать состоящей из множества точек зрения, при наблюдении из которых один объект заслоняет другой. При таком подходе вводится понятие "прямизны", которое воплощается в термине "прямая линия" (или просто "прямая"). Можно считать, что мы абстрагировали понятия "точка" и "прямая" из окружающего мира. В нашем повседневном опыте коренится еще одно представление - о расстоянии АВ между точками А и В. (Мы говорим также о "длине" отрезка АВ.) О расстоянии мы судим, сравнивая его с некоторым эталоном. Одна из возможных единиц длины - метр; изготовив копии с эталона метра, мы сравниваем расстояния и говорим, что расстояние АВ больше (>), равно (=) или меньше (
(эллиптический параболоид)
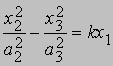
(гиперболический параболоид). Некоторые из этих поверхностей являются "линейчатыми". Это означает, что через каждую точку такой поверхности можно провести по крайней мере две прямые, целиком лежащие на этой поверхности; в результате получим два семейства прямых, любое из которых образует всю поверхность. Эти прямые называют образующими. Если мы ограничимся рассмотрением какой-нибудь одной плоскости, например, положив для этого в уравнении квадратичной поверхности x3 = 0, то получим уравнения конических сечений - кривых, по которым эти поверхности пересекают плоскость x3 = 0. Это - эллипс (частным случаем которого является окружность), гипербола и парабола
(см. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ; КОНИЧЕСКИЕ СЕЧЕНИЯ). Исследование геометрических мест точек, заданных уравнениями, порядок которых больше двух, значительно сложнее. В 1704 И.Ньютон (1643-1727) классифицировал кубические кривые, и с тех пор кривые и поверхности третьего и четвертого порядков стали предметом интенсивного изучения. Хотя методы Декарта существенно упростили идеи греческой геометрии, они же породили много новых трудностей. Некоторые из этих трудностей были преодолены с помощью средств, которыми располагал математический анализ 19 в. Справиться с другими удалось лишь позднее, когда была создана т. н. алгебраическая геометрия (см. АЛГЕБРАИЧЕСКАЯ ГЕОМЕТРИЯ). Интересно отметить, что аналитическая геометрия Ферма и Декарта появилась как раз в то время, когда И. Кеплер (1571-1630), исходя из многочисленных астрономических наблюдений, сделал вывод о том, что планеты движутся по эллипсам, в одном из фокусов которых расположено Солнце. Это подготовило почву для открытия Ньютоном закона всемирного тяготения. Природа даже тогда, когда речь шла о местоположениях далеких планет, соответствовала описанию человеком его представлений о пространстве! Нужно ли удивляться, что для Ньютона "абсолютное пространство по самой своей сущности, безотносительно к чему бы то ни было внешнему, остается всегда одинаковым и неподвижным". Для великого современника Ньютона Г. фон Лейбница (1646-1716) пространство было совокупностью всех возможных отношений расстояния. В следующем разделе мы будем понимать слово "пространство" в более ограниченном смысле.
Проективная геометрия. Наступление 17 в. ознаменовалось настоящим взрывом научной активности. В развитии математики началась новая эра; наряду с Декартом Ж. Дезарг (1593-1662) и Б. Паскаль (1623-1662) попытались по-новому и критически взглянуть на старую евклидову геометрию, чтобы понять, все ли ее результаты представимы в терминах одних лишь точек и прямых. К возникшей в результате такого критического пересмотра проективной геометрии можно подойти, вводя новую систему аксиом, но гораздо поучительнее рассмотреть наши предыдущие исходные допущения и попытаться понять, как их надлежит изменить. Если следовать зрительным восприятиям, то первое, что сразу подпадает под подозрение, - это постулат о параллельных прямых. Нам кажется, что такие прямые все-таки пересекаются в бесконечности. Предположим, что это действительно так, и дополним евклидову плоскость одной "идеальной точкой" или "бесконечно удаленной точкой", общей для любого множества параллельных прямых. Тогда утверждение о том, что прямые l и m параллельны, перейдет в утверждение о том, что прямые l и m пересекаются в бесконечности. Необходимо доказать, что все такие идеальные точки ведут себя так, как если бы они принадлежали "идеальной прямой", которая обладает всеми свойствами, которыми по предположению обладают обычные прямые. Доказательство этого утверждения основывается на знаменитой теореме Дезарга: если соответствующие вершины двух треугольников можно соединить тремя прямыми, пересекающимися в одной точке, то соответствующие стороны пересекаются в точках, лежащих на одной прямой, и обратно. Обосновав присоединение идеальных элементов к евклидовой плоскости, мы можем теперь сказать, что любые две прямые имеют точку пересечения, и в этом заключается основное отличие проективной геометрии. Аналогичным образом мы можем присоединить к трехмерному евклидову пространству "бесконечно удаленную плоскость" и построить проективное пространство любой размерности. Заметим, что теперь мы можем полностью отказаться от понятия "расстояние". Нужно подчеркнуть, что проективная геометрия не есть что-то абстрактное, практически не связанное с внешним миром. Рассмотрим произвольную точку Р и любую плоскость p, не проходящую через точку Р, в обычной евклидовой геометрии. Любая плоскость p1, проходящая через Р, пересекается с плоскостью p по некоторой прямой l1; в частности, плоскость pҐ , проходящая через точку Р и параллельная плоскости p, пересекается с p по прямой lҐ , бесконечно удаленной прямой, лежащей в плоскости p. Таким образом, существует взаимно однозначное соответствие между плоскостями, проходящими через точку Р, и прямыми, лежащими в плоскости p. Если воспользоваться интерпретацией точка = прямая, проходящая через Р, прямая = плоскость, проходящая через Р, то можно проверить, что все аксиомы проективной геометрии выполняются, а потому "пучок" прямых и плоскостей, проходящих через точку Р, образует проективную геометрию плоскости. Вклад Паскаля в геометрию заключается в том, что он показал проективную природу известных со времен Аполлония свойств конических сечений, которые позднее были переведены Декартом на алгебраический язык. Эта работа была завершена Ф. де Лаиром (1640-1718), и, хотя дальнейшее развитие проективной геометрии прервалось и затем продолжилось лишь в 19 в., начало критическому анализу понятия длины было положено.
Непрерывность. Понятие касательной к кривой восходит по крайней мере к Архимеду, но только после того, как Ферма и Ньютон осознали его значение для дифференциального исчисления, это понятие обрело удобную для приложений явную форму. Однако прошло немало лет, прежде чем О.Коши (1789-1857) придал строгость огромному числу теорем, разложениям в степенные ряды, решениям дифференциальных уравнений и т.п., что позволило математическому анализу занять в математике место, сравнимое с геометрией. Понятие числа точек на прямой ничему не соответствует в нашем опыте визуального восприятия пространства, и именно это привело Зенона Элейского к упомянутым выше комментариям. Есть два способа интерпретации понятия непрерывности в терминах интуитивных представлений об окружающем нас мире: 1) через скрупулезный анализ отношений между точками и прямыми и 2) в терминах движения, т.е. средствами математического анализа (см. МАТЕМАТИЧЕСКИЙ АНАЛИЗ).
Конечная геометрия. Хотя целые числа возникают не обязательно в связи с точками прямой, тем не менее естественно рассматривать их как числа, представляющие кратные некоторого единичного отрезка. Это позволяет придать рациональным числам геометрическую интерпретацию, известную еще древним грекам. Однако такой подход к числу недостаточно тонок и сталкивается с трудностями, на которые и указал Зенон; наша концепция пространства включает в себя понятие числа, но для определения чисел понятие пространства не подходит. Возвращаясь к аксиомам проективной геометрии
(см. ПРОЕКТИВНАЯ ГЕОМЕТРИЯ),
заметим, что они не содержат понятия длины и не имеют следствием бесконечность числа точек на прямой. То, что число точек на прямой может быть конечным, подтверждается следующим примером. Предположим, что под точками мы понимаем 15 символов (ab), (ac), (ad), (ae), (af), (bc), (bd), (be), (bf), (cd), (ce), (cf), (de), (df), (ef), где (ij) = (ji). Существуют 35 прямых, каждая из которых содержит три и только три из этих точек. Такие прямые можно разбить на два типа: 1) прямая типа I содержит три точки вида (аb), (bc), (ca); таких прямых 20; 2) прямая типа II содержит три точки вида (ab), (cd), (ef); таких прямых 15. Любая тройка точек, не принадлежащих ни к одному из этих двух типов, определяет некоторую плоскость; существуют 15 плоскостей, каждая из которых содержит семь точек и семь прямых. На прилагаемом рис. 5 показаны расположения точек и прямых на одной из этих плоскостей. (Заметим, что окружность представляет в конечной геометрии прямую.) Нетрудно проверить, что все аксиомы проективной геометрии выполняются, из чего мы заключаем, что они непротиворечивы, но такая геометрия не очень соответствует нашему представлению о пространстве. Чтобы перебросить мост между привычным понятием пространства и построенной нами геометрией, необходимо исследовать возможную связь между точками на прямой и числами арифметики.
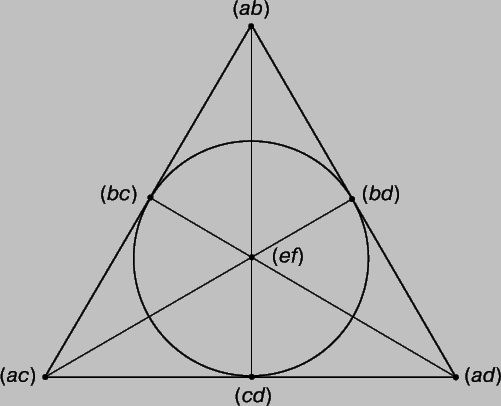
Рис. 5. ПЛОСКОСТЬ ОПРЕДЕЛЯЕТСЯ любыми тремя точками, не лежащими на одной прямой. Например, (ab), (ef), (bc) определяют одну плоскость.
Первым, кто предложил средства, позволяющие геометрически определять операции сложения и умножения, был немецкий математик К.Штаудт (1798-1867), но именно Д. Гильберт (1862-1943) продемонстрировал, что законы арифметики в их геометрической интерпретации зависят от двух теорем - Дезарга и Паппа. В случае конечной геометрии из теоремы Дезарга следует теорема Паппа, а потому если она верна, то верна и теорема Паппа. В этом случае и сложение, и умножение ассоциативны, коммутативны и дистрибутивны, и координаты, которые можно поставить в соответствие точкам на прямой, могут образовать конечное "поле". Если число точек на прямой бесконечно (например, если точки на прямой, за исключением бесконечно удаленной точки, могут быть поставлены во взаимно однозначное соответствие с рациональными числами), то "сложение" точек на прямой ассоциативно и коммутативно при условии, что выполняется теорема Дезарга. Если размерность n > 2, то это заведомо так. Однако из семи аксиом проективной геометрии теорема Паппа не следует; это означает, что умножение, будучи ассоциативным, необязательно коммутативно. При n = 2 теорема Дезарга может не выполняться, и "алгебра" точек на прямой еще более усложняется. Возможные недезарговы плоскости исследуются с 1902, но многое еще остается неизвестным. Если потребовать, чтобы для каждого действительного числа нашлась соответствующая ему точка на прямой, то мы получим т.н. "непрерывную" геометрию. Это требование выполняется введением дополнительного предположения, которое в свою очередь можно использовать для доказательства теоремы Паппа. Такая аксиома непрерывности описывает тот аспект нашего понятия пространства, который был Лейбницем охарактеризован как "лабиринт континуума". Тем не менее роль алгебры в геометрии стала очевидна, и в дальнейшем обе эти ветви математики стали нерасторжимы.
Дифференциальная геометрия. Определив касательную к плоской кривой в точке (y1, y2) с помощью "углового коэффициента" m = dy2/dy1, мы можем записать ее уравнение в виде
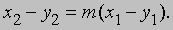
Записанное с помощью дифференциалов, это уравнение принимает вид
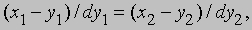
и его непосредственное обобщение приводит к уравнениям касательной к неплоской кривой в точке (y1, y2, y3):
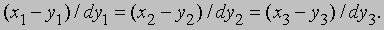
В то время как понятие углового коэффициента не допускает обобщения, понятие направляющего числа легко обобщается, и в качестве направляющих чисел рассматриваемой прямой можно принять дифференциалы. Уравнение соприкасающейся плоскости (плоскости касательных) к неплоской кривой задается определителем
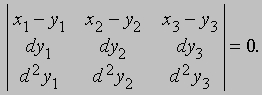
Все эти уравнения имеют явный вид, если рассматриваемое геометрическое место точек задано аналитически, например, параметрически формулами y1 = y1 (t), y2 = y2 (t), y3 = y3 (t). Дифференциальная геометрия стала самостоятельным разделом математики после того, как Б.Риман (1826-1866) заметил, что теорема Пифагора допускает дальнейшее обобщение, и предложил определять меру длины как
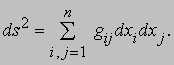
При n = 3 и gij = 1 (если i = j) и gij = 0 (если i № j) мы получаем евклидову геометрию в декартовых (прямоугольных) координатах; другие возможные выборы величин gij приводят к множеству новых геометрических систем, в частности, к геометрии специальной и общей теорий относительности. В конце 19 в. для разработки этих идей был изобретен тензорный анализ, который оказался одним из наиболее подходящих языков для современной физики. Таким образом, методы математического анализа привели нас к идеям, весьма отличным от тех, которые были известны древним грекам. В частности, огромное значение получило понятие "геодезической" - линии, целиком лежащей на поверхности и являющейся кратчайшим путем между двумя точками. Если уравнение некоторой поверхности записать в параметрическом виде: x1 = x1 (u,v), x2 = x2 (u,v), x3 = x3 (u,v), то геометрические места точек u = const, v = const называются "параметрическими кривыми" этой поверхности, а параметры (u,v) задают на этой поверхности "криволинейные координаты". На поверхности Земли мы определяем свое местонахождение, указывая "широту" и "долготу"; из этих двух систем параметрических кривых линии долготы являются большими кругами и, следовательно, геодезическими. В случае декартовой геометрии параметрическими кривыми служат прямые, параллельные осям координат, и все такие прямые - геодезические.
См. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ. Неевклидова геометрия. Смелое допущение Евклида о параллельных прямых, содержавшееся в его знаменитом пятом постулате, почти две тысячи лет было для математиков источником смутного беспокойства, но серьезные попытки доказать его на основе иных допущений были предприняты только в 18 в. И хотя они оказались безуспешными, математикам все же удалось показать, что постулат о параллельных Евклида эквивалентен требованию равенства суммы углов треугольника двум прямым углам, или, что то же, p радианам. Поэтому скорее психологическим, чем математическим прорывом стало осознание существования двух других возможных вариантов: 1) сумма углов треугольника всегда больше p; в этом случае параллельных прямых не существует, и любые две прямые пересекаются; 2) сумма углов треугольника всегда меньше p; в этом случае для любой точки Р, не лежащей на данной прямой l, существуют две прямые l' и l ", проходящие через Р и параллельные данной прямой l, и любая прямая, лежащая внутри угла, заключенного между l' и l ", не пересекается с l. Непротиворечивость второго варианта была осознана К. Гауссом (1777-1855), но впервые опубликована независимо друг от друга Я. Бойяи (1802-1860) и Н.И.Лобачевским (1792-1856) в 30-х годах 19 в. Риман был первым, кто понял, что первый вариант реализуется в сферической геометрии, развитой для нужд астрономии и мореплавания. Было бы ошибкой думать, будто математика на протяжении столетий не претерпела никаких изменений. Постижение тонких идей происходит медленно, и когда мы оглядываемся назад, в прошлое, наши величайшие достижения нередко представляются очень простыми. А. Кэли (1821-1895) и Ф. Клейн (1849-1925) прояснили связь между двумя упомянутыми вариантами, разработав в аналитической форме то, что ими было названо "эллиптической" и "гиперболической" геометриями. Евклидова геометрия является предельным случаем каждой из них, и это верно в отношении любой из аналитических формул таких геометрий. Большие круги (геодезические) на сфере, являющейся поверхностью постоянной положительной кривизны, играют роль прямых и порождают эллиптическую геометрию; аналогичным образом, на поверхности постоянной отрицательной кривизны геодезические порождают гиперболическую геометрию. Можно построить и другие наглядные и поучительные модели эллиптической и гиперболической геометрий, но важно сознавать, что все эти модели содержатся в более общем подходе Римана. Трудно переоценить философское значение этих идей. Человек словно снял темные очки и увидел свое представление о пространстве "при дневном свете", что открыло новые, более интересные и захватывающие возможности, чем он мог себе вообразить. То, что Гаусс предпринял попытку измерить сумму углов треугольника, образованного тремя горными вершинами в Германии, было естественным следствием его понимания того, что постулат Евклида о параллельных явился результатом выбора из ряда возможностей, хотя выбора, несомненно, наилучшего для наших повседневных нужд. И хотя Гауссу не удалось обнаружить никаких отклонений от p, выходящих за пределы допустимой экспериментальной ошибки, это отнюдь не положило конец попыткам предпринять аналогичные крупномасштабные измерения с помощью гигантских телескопов и электронных устройств (см. НЕЕВКЛИДОВА ГЕОМЕТРИЯ). В последние десятилетия наши представления о пространстве сильно изменились под воздействием повсеместного принятия в физике концепции "пространства-времени". Связывание воедино двух фундаментальных понятий вынуждает нас перенести все внимание с "положения" на "событие". Выбирая из многообразия римановых метрик некоторую, в чем-то более предпочтительную, мы может более удовлетворительным образом скоординировать результаты современной физики. См. ОТНОСИТЕЛЬНОСТЬ.
Понятие группы. Расцвет геометрических идей в 19 в. убедительно свидетельствовал о необычайной жизненности математических исследований в целом. Но, возможно, самым важным событием в развитии математического мышления в 19 в. стала постепенная кристаллизация понятия "группы" в алгебре и осознание его значения для геометрии. Древние греки вполне могли бы натолкнуться на эту идею, будь они более настойчивы в поиске внутреннего смысла симметрии. К проблеме симметрии можно подходить двояко. Если геометрическая фигура остается инвариантной относительно вращения или, более общо, относительно какого-нибудь "преобразования", то можно выписать некоторую систему уравнений, выражающих эти преобразования аналитически. Но возможен и другой подход: мы можем представить себе, что геометрическая фигура остается неизменной, а меняется избранный нами способ ее описания относительно системы координат. По существу речь идет о двух возможных способах интерпретации одного и того же преобразования, но иногда одна интерпретация бывает предпочтительнее другой. Если мы имеем в виду все возможные линейные преобразования, которые оставляют фигуру инвариантной, то говорим, что эти преобразования образуют "группу", которую абстрактно можно определить следующим образом. Если обозначить эти преобразования Т1, Т2 и т.д., а совокупность всех таких преобразований - G, то для любых двух преобразований Ti и Tj из G должны выполняться следующие условия: I. TiTj = Tk также принадлежит G; II. Ti (TjTk) = (TiTj)Tk (свойство ассоциативности); III. В G существует некоторое преобразование Т0, называемое тождественным преобразованием или единицей, такое, что TiT0 = T0Ti = Ti; IV. Для каждого Ti из G существует "обратное преобразование" Ti-1, такое, что TiTi-1 = Ti-1Ti = T0. Число g преобразований Т, содержащихся в G, называется "порядком" группы G. Существует 6 симметрий треугольника, они представлены на рис. 6. Нетрудно проверить, что если ограничиться только вращениями, то для тетраэдра g = 12, для куба и октаэдра g = 24, а для икосаэдра и додекаэдра g = 60. Если же кроме вращений допустить отражения и отражения с вращениями, то число g возрастет вдвое. То, что у куба и октаэдра должна быть одна и та же группа вращений, неудивительно, т.к. вершины одного многогранника служат центрами граней другого. Аналогичное утверждение справедливо относительно икосаэдра и додекаэдра. Эти фигура "двойственны" друг другу, тогда как тетраэдр "самодвойствен".
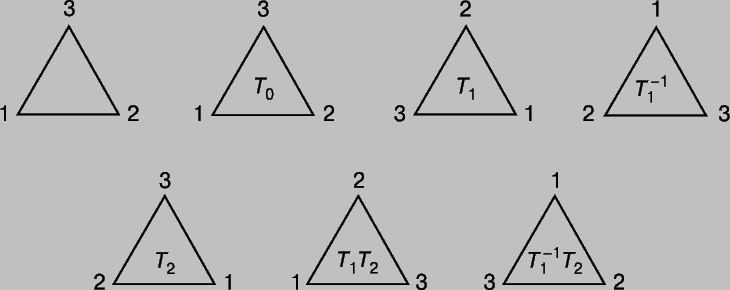
Рис. 6. ШЕСТЬ СИММЕТРИЙ ТРЕУГОЛЬНИКА. Любой из изображенных здесь треугольников может быть получен из первого соответствующим поворотом.
Все преобразования, о которых шла речь, линейны; они переводят точку в точку, прямую - в прямую и плоскость - в плоскость. Такие "коллинеации" имеют особое значение для описания нашего представления о пространстве, основанного на точках и прямых. Клейн первым понял, что множество всех линейных преобразований, оставляющих метрику инвариантной, позволяет адекватно описывать рассматриваемую геометрию, и это привело Клейна к классификации геометрий по их группам коллинеаций. В проективной геометрии метрика отсутствует, поэтому соответствующая ей группа называется "полной линейной группой". В евклидовой геометрии любое вращение оставляет инвариантной сумму квадратов координат, и соответствующая коллинеация называется "ортогональной"; т.к. комбинация двух ортогональных преобразований есть снова ортогональное преобразование, все ортогональные преобразования образуют "ортогональную группу". Параллельные переносы также оставляют метрику инвариантной, поэтому группа "перемещений фигуры как твердого тела" содержит ортогональную группу в качестве своей нормальной подгруппы. Такой подход к изучению геометрии был предложен Клейном в его Эрлангенской программе (1872), которая явилась большим шагом вперед, поскольку предлагала единую точку зрения на ранее существовавшие различные геометрии. Понятие группы получило дальнейшее развитие. До сих пор мы предполагали, что каждое преобразование линейно, но это ограничение несущественно, коль скоро каждое преобразование имеет обратное, которое однозначно определено. Исследование таких "бирациональных" преобразований в общем виде началось с работ Л. Кремоны (1830-1903). В 1870 было доказано, что любое бирациональное преобразование может быть порождено составными квадратичными преобразованиями. Важно подчеркнуть существование некоторых особых точек или геометрических мест, для которых взаимно однозначное соответствие нарушается; именно это обстоятельство порождает специфические проблемы алгебраической геометрии, над решением которых билось немало математиков.
См. также АЛГЕБРА АБСТРАКТНАЯ.
Топология. Общая теория групп преобразований была построена С. Ли (1842-1899), который почти в одиночку возделал огромную территорию математики, оказавшую впоследствии воздействие почти на все ее разделы. Что же касается влияния Ли на геометрию, то оно сказалось прежде всего на расширении самого смысла термина "геометрия", в результате чего граница между геометрией и анализом оказалась размытой. Та часть "ничейной земли", в которой алгебраический характер преобразования предается забвению, получила название "топологии". Топология имеет дело с взаимно однозначными и непрерывными преобразованиями, называемыми "гомеоморфизмами". Изучение топологических пространств позволило открыть множество красивейших теорем. С 1895, когда А.Пуанкаре впервые в явном виде рассмотрел гомеоморфные преобразования топологических пространств, и по сей день топология находится в состоянии интенсивного беспрецедентного развития. Поясним суть ее проблем на одном примере. Возьмем некоторую поверхность и будем ее рассматривать как резиновую пленку, которую можно сжимать и растягивать, но не рвать. Тогда никакие из разрешенных операций не могут преобразовать сферу в тор (бублик); число дыр в поверхности называется ее "родом" и является "топологическим инвариантом". Аналогичный инвариант существует и для односторонних поверхностей, таких как лист Мебиуса (см. также ТОПОЛОГИЯ). Существует масса примеров, когда к топологии обращаются в поисках новых, стимулирующих идей и подходов, чувствуя, что иначе "не пробиться", как, например, в теории контурного интегрирования Коши. Наше представление о пространстве - это наиболее изученная модель, позволяющая лучше всего понять те абстракции, которые и составляют суть математики в целом. Именно такая интерпретация слова "геометрия" позволила уяснить истинное значение этой науки и причину, по которой люди занимаются ее изучением на протяжении вот уже 2500 лет.
ГЕОМЕТРИЧЕСКАЯ АБСТРАКЦИЯ - ГЕОМЕТРИ́ЧЕСКАЯ АБСТРА́КЦИЯ, один из видов абстрактного искусства (см. АБСТРАКТНОЕ ИСКУССТВО), предпочитающий композиции, в основе которых - строгая ритмика геометрических или (в скульптуре) стереометрических фигур. Ее ранние варианты (отчасти орфизм (см. ОРФИЗМ) Р. Делоне (см. ДЕЛОНЕ Робер) и Ф. Купки (см. КУПКА Франтишек), а также супрематизм (см. СУПРЕМАТИЗМ) К. С. Малевича (см. МАЛЕВИЧ Казимир Северинович) и неопластицизм (см. НЕОПЛАСТИЦИЗМ) П. Мондриана (см. МОНДРИАН Пит)) сочетают рационализм с романтикой, тяготея к построению «абсолютных» красочно-графических монументальных символов, выражающих мистические законы космоса. В то же время геометрическая абстракция впитала в себя и технократический пафос конструктивизма (см. КОНСТРУКТИВИЗМ). Во второй половине 20 в. в таких течениях, как оп-арт (см. ОП-АРТ) и постживописная абстракция (см. ПОСТЖИВОПИСНАЯ АБСТРАКЦИЯ), геометрическая абстракция сохраняет свой «рационалистический мистицизм», еще теснее сближаясь с многообразной динамикой современной жизни.
ГЕОМЕТРИЧЕСКАЯ абстракция - один из видов абстрактного искусства, предпочитающий композиции, в основе которых - строгая ритмика геометрических или (в скульптуре) стереометрических фигур. Ее ранние варианты (отчасти орфизм Р. Делоне и Ф. Купки, а также супрематизм К. С. Малевича и неопластицизм П. Мондриана) сочетают рационализм с романтикой, тяготея к построению "абсолютных" красочно-графических монументальных символов, выражающих мистические законы космоса. В то же время геометрическая абстракция впитала в себя и технократический пафос конструктивизма. Во второй половине 20 в. в таких течениях, как оп-арт и постживописная абстракция, геометрическая абстракция сохраняет свой "рационалистический мистицизм", еще теснее сближаясь с многообразной динамикой современной жизни.
Геометри́ческая изомери́я - то же, что цис-транс-изомерия.
* * *
ГЕОМЕТРИЧЕСКАЯ ИЗОМЕРИЯ - ГЕОМЕТРИ́ЧЕСКАЯ ИЗОМЕРИ́Я, то же, что цис-транс-изомерия (см. ЦИС-ТРАНС-ИЗОМЕРИЯ).
ГЕОМЕТРИЧЕСКАЯ ИЗОМЕРИЯ - то же, что цис-транс-изомерия.
Геометри́ческая о́птика - раздел оптики, в котором распространение света в прозрачных средах рассматривается на основе представления о световом луче как линии, вдоль которой распространяется световая энергия. Законы геометрической оптики применяются для расчётов построения изображения при прохождении света через оптические системы.
* * *
ГЕОМЕТРИЧЕСКАЯ ОПТИКА - ГЕОМЕТРИ́ЧЕСКАЯ О́ПТИКА, раздел оптики, в котором распространение света в прозрачных средах рассматривается на основе представления о световом луче как линии, вдоль которой распространяется световая энергия. Законы геометрической оптики применяются для расчетов построения изображения при прохождении света через оптические системы.
ГЕОМЕТРИЧЕСКАЯ ОПТИКА - раздел оптики, в котором распространение света в прозрачных средах рассматривается на основе представления о световом луче как линии, вдоль которой распространяется световая энергия. Законы геометрической оптики применяются для расчетов построения изображения при прохождении света через оптические системы.
ГЕОМЕТРИЧЕСКАЯ ОПТИКА, раздел оптики, в котором распространение света в прозрачных средах описывается с помощью представления о световых лучах, а волновые и квантовые свойства не учитываются. Основные законы геометрической оптики - отражения света и преломления света на границе раздела 2 однородных сред - в основном достаточны для построения изображений оптических в оптических системах, а также для описания аберраций и методов их исправления. По аналогии с геометрической оптикой применяется также понятие геометрическая акустики.
преломление. лучепреломление.
преломить, -ся.
аберрация. астигматизм. дисторсия. кома.
каустика, каустическая поверхность.
фокус. фокальный.
диоптрия.
диоптрика.
увеличительный (# линза). <-> уменьшительный.
менисковые системы.
гомоцентрический пучок лучей.
параксиальный.
виньетирование.
эйконал.
анаморфоз. анаморфирование. анаморфоты.
растр. растровая оптика.
катоптрика.
Геометри́ческая прогре́ссия - последовательность чисел, из которых каждое следующее получается из предыдущего умножением на постоянное число q, называемое знаменателем геометрической прогрессии, например 2, 8, 32, 128, ..., q = 4.
* * *
ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ - ГЕОМЕТРИ́ЧЕСКАЯ ПРОГРЕ́ССИЯ, последовательность чисел, из которых каждое следующее получается из предыдущего умножением на постоянное число q, называемого знаменателем геометрической прогрессии, напр., 2, 8, 32, 128,..., q = 4.
ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ - последовательность чисел, из которых каждое следующее получается из предыдущего умножением на постоянное число q, называемого знаменателем геометрической прогрессии, напр., 2, 8, 32, 128,..., q = 4.
ГЕОМЕТРИЧЕСКАЯ РЕЗЬБА ПО ДЕРЕВУ - ГЕОМЕТРИ́ЧЕСКАЯ РЕЗЬБА́ ПО ДЕ́РЕВУ, один из самых древних и распространенных видов деревянной орнаментальной резьбы. Выполняется в виде выемок двух-, трех-, четырехгранной формы, которые в сочетании дают большое число разнообразных композиций. Главный инструмент резчика - резец со скошенным концом, так называемый «косячок».
Геометрическая резьба подразделяется на две основные разновидности: трехгранно-выемчатая резьба и ногтевидная (или скобчатая).
В основе первой лежит заглубленная внутрь трехгранная пирамидка, из которой формируются разнообразные орнаменты. Ногтевидная резьба получила свое название от полукруглого углубления - «ноготка», наносимого полукруглой стамеской. Сочетания «ноготков» дают более сложные узоры - листики, трилистники, глазки.
Орнаментика геометрической резьбы восходит к древним языческим символам. Например, один из наиболее распространенных элементов - розетка - был связан с культом солнца. Розетки и сияния присутствуют во всех композициях, выполненных в технике трехгранно-выемчатой резьбы. Геометрическая резьба использовалась в домовом декоре Русского Севера и при украшении прялок (см. ПРЯЛКА) и различных предметов домашней утвари - вальков, рубелей, трепал. Геометрический узор встречается на предметах из новгородских раскопок 10-12 веков. Подобные орнаменты украшают изделия западноевропейских ремесленников, мастеров Средней Азии.
В конце 19 века, на гребне волны интереса к народному искусству, геометрическую резьбу вновь начинают широко применять в архитектуре, при оформлении мебели и деталей интерьера. Эту технику использовали столярные мастерские в Талашкине (см. ТАЛАШКИНО), Абрамцеве (см. АБРАМЦЕВО), Нижнем Новгороде, эскизы для орнамента делали профессиональные художники. Сегодня геометрическая резьба применяется главным образом при отделке мелких бытовых предметов и в сувенирном производстве.
нареч. качеств.-обстоят.
1. В соответствии с законами и принципами геометрии [геометрия I 1.] как раздела математики, изучающего пространственные отношения и формы.
2. Геометрическим способом.
Геометри́чески неизменя́емая систе́ма (в строительной механике), система соединённых между собой тел (например, стержней, дисков), изменение формы которых невозможно без деформации материала. Все несущие конструкции зданий и сооружений являются геометрически неизменяемыми системами.
* * *
ГЕОМЕТРИЧЕСКИ НЕИЗМЕНЯЕМАЯ СИСТЕМА - ГЕОМЕТРИ́ЧЕСКИ НЕИЗМЕНЯ́ЕМАЯ СИСТЕ́МА, в строительной механике - система соединенных между собой тел (напр., стержней, дисков), изменение формы которых невозможно без деформации материала. Все несущие конструкции зданий и сооружений являются геометрически неизменяемыми системами.
ГЕОМЕТРИЧЕСКИ НЕИЗМЕНЯЕМАЯ система - в строительной механике - система соединенных между собой тел (напр., стержней, дисков), изменение формы которых невозможно без деформации материала. Все несущие конструкции зданий и сооружений являются геометрически неизменяемыми системами.
Геометри́ческие построе́ния - приёмы, позволяющие по графически данным элементам (точкам, прямым, окружностям) найти (построить) с помощью наперёд заданных средств другие элементы, связанные с данными некоторыми условиями. Наиболее известны построения с помощью циркуля и линейки (односторонней, без делений). В связи с этим типом геометрических построений возникли классические задачи древности: квадратура круга, трисекция угла и удвоение куба.
* * *
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ - ГЕОМЕТРИ́ЧЕСКИЕ ПОСТРОЕ́НИЯ, приемы, позволяющие по графически данным элементам (точкам, прямым, окружностям) найти (построить) с помощью наперед заданных средств другие элементы, связанные с данными некоторыми условиями. Наиболее известны построения с помощью циркуля и линейки (односторонней, без делений). В связи с этим типом геометрических построений возникли классические задачи древности: квадратура круга (см. КВАДРАТУРА КРУГА), трисекция угла и удвоение куба (см. УДВОЕНИЕ КУБА).
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ - приемы, позволяющие по графически данным элементам (точкам, прямым, окружностям) найти (построить) с помощью наперед заданных средств другие элементы, связанные с данными некоторыми условиями. Наиболее известны построения с помощью циркуля и линейки (односторонней, без делений). В связи с этим типом геометрических построений возникли классические задачи древности: квадратура круга, трисекция угла и удвоение куба.
прил.
1. соотн. с сущ. геометрия I 1., связанный с ним
2. Свойственный геометрии [геометрия I 1.], характерный для неё.
3. Образованный линиями и схематическими фигурами (треугольниками, окружностями, прямоугольниками и т.п.).
ГЕОМЕТРИ́ЧЕСКИЙ, геометрическая, геометрическое (научн.).
1. прил. к геометрия. Геометрическая теорема. Геометрические тела (шар, конус, пирамида, призма и др.). Геометрические фигуры (треугольник, квадрат, круг и др.).
2. Состоящий из линий, точек, геометрических фигур (спец.). Геометрический орнамент. Геометрический стиль. Геометрическая резьба.
ГЕОМЕТРИ́ЧЕСКИЙ -ая, -ое.
1. к Геоме́трия. Г-ая задача. Г-ая аксиома. Г-ая теорема. Г-ое понятие. Г-ая прогрессия.
2. Состоящий из линий, точек и схематических фигур (треугольников, конусов, кривых и т.п.). Г. орнамент.
◁ Геометри́чески, нареч. Г. расчерченные дорожки. Г. точно проложить улицы.
-ая, -ое.
1. прил. к геометрия.
Геометрическая задача. Геометрическая
аксиома. Геометрический метод.
2. Состоящий из линий, точек и схематических фигур (треугольников, конусов, кривых и т. п.).
Геометрический орнамент.
геометри́ческий, геометри́ческая, геометри́ческое, геометри́ческие, геометри́ческого, геометри́ческой, геометри́ческих, геометри́ческому, геометри́ческим, геометри́ческую, геометри́ческою, геометри́ческими, геометри́ческом, геометри́ческ, геометри́ческа, геометри́ческо, геометри́чески
геометри́ческий
- прил. от сл. геометрия;
г-ое среднее двух положительных чисел - квадратный корень из произведения этих чисел;
г-ая прогрессия - ряд чисел, в котором каждое число, начиная со второго, есть геометрическое среднее своих соседей;
г-ое место точек - совокупность точек, удовлетворяющих нек-рому условию, напр.: окружность есть г-ое место точек на плоскости, равноотстоящих от данной точки (центра этой окружности).
Геометри́ческий стиль - в искусстве, ранняя (IX-VIII вв. до н. э.) стадия развития древнегреческого искусства: геометрический орнамент, геометризованной фигуры людей и животных в вазописи, схематичные бронзовые статуэтки.
* * *
ГЕОМЕТРИЧЕСКИЙ СТИЛЬ - ГЕОМЕТРИ́ЧЕСКИЙ СТИЛЬ в искусстве, ранняя (9-8 вв. до н. э.) стадия развития древнегреческого искусства: геометрический орнамент, геометризованные фигуры людей и животных в вазописи, схематичные бронзовые статуэтки.
ГЕОМЕТРИЧЕСКИЙ СТИЛЬ в искусстве - ранняя (9-8 вв. до н. э.) стадия развития древнегреческого искусства: геометрический орнамент, геометризованные фигуры людей и животных в вазописи, схематичные бронзовые статуэтки.

Геометрический стиль.
Аттическая амфора.
2-я четверть 8 в. до н.э.
ГЕОМЕТРИЧЕСКИЙ СТИЛЬ, одна из ранних стадий (9 - 8 вв. до нашей эры) развития древнегреческого искусства. Наиболее ярко проявился в вазописи, отчасти в мелкой пластике и глиптике: геометрический орнамент, геометризованные фигуры людей и животных в росписи ваз, схематичные статуэтки.
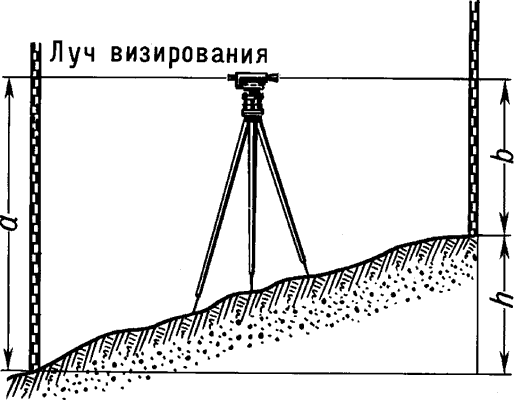
Геометри́ческое нивели́рование - метод определения превышений путём визирования горизонтальным лучом с помощью нивелира и отсчёта разности высот по рейкам. Точность отсчёта по рейкам 1-2 мм (техническое нивелирование) и до 0,1 мм (высокоточное нивелирование).
* * *
ГЕОМЕТРИЧЕСКОЕ НИВЕЛИРОВАНИЕ - ГЕОМЕТРИ́ЧЕСКОЕ НИВЕЛИ́РОВАНИЕ, метод определения превышений путем визирования горизонтальным лучом с помощью нивелира (см. НИВЕЛИР) и отсчета разности высот по рейкам (см. РЕЙКА) . Точность отсчета по рейкам 1-2 мм (техническое нивелирование) и до 0,1 мм (высокоточное нивелирование).
ГЕОМЕТРИЧЕСКОЕ нивелирование - метод определения превышений путем визирования горизонтальным лучом с помощью нивелира и отсчета разности высот по рейкам. Точность отсчета по рейкам 1-2 мм (техническое нивелирование) и до 0,1 мм (высокоточное нивелирование).
Геометри́ческое преобразова́ние - взаимно однозначное отображение прямой, плоскости или пространства на себя. Примеры геометрического преобразования: подобие, движение, аффинное преобразование.
* * *
ГЕОМЕТРИЧЕСКОЕ ПРЕОБРАЗОВАНИЕ - ГЕОМЕТРИ́ЧЕСКОЕ ПРЕОБРАЗОВА́НИЕ, взаимно однозначное отображение прямой, плоскости или пространства на себя. Примеры геометрического преобразования: подобие (см. ПОДОБИЕ), движение (см. ДВИЖЕНИЕ (в геометрии)), аффинное преобразование (см. АФФИННОЕ ПРЕОБРАЗОВАНИЕ).
ГЕОМЕТРИЧЕСКОЕ ПРЕОБРАЗОВАНИЕ - взаимно однозначное отображение прямой, плоскости или пространства на себя. Примеры геометрического преобразования: подобие, движение, аффинное преобразование.
геометрическое пространство - непрерывная последовательность положений, мест;
пространство положений;
система, состоящая из элементов, которые характеризуются только своим положением;
сфера, среда существования объектов (# - непрерывное пространство).
↓ квадрант. октант.
объемный, движение, физическое поле, РАСПОЛОЖЕНИЕ
♥ место
Геометри́ческое сре́днее - величина (а*), равная корню n-й степени из произведения п данных величин (а1, а2, … аn):
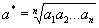 .
.
Геометрическое среднее двух чисел а, b, равное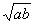 , называют также средним пропорциональным между а и b.
, называют также средним пропорциональным между а и b.
* * *
ГЕОМЕТРИЧЕСКОЕ СРЕДНЕЕ - ГЕОМЕТРИ́ЧЕСКОЕ СРЕ́ДНЕЕ, величина (a*), равная корню n-й степени из произведения n данных величин (а1, а2,...,аn):
Геометрическое среднее двух чисел а, b, равное , называется также средним пропорциональным между а и b.
ГЕОМЕТРИЧЕСКОЕ СРЕДНЕЕ - величина (a*), равная корню n-й степени из произведения n данных величин (а1, а2,...,аn):Геометрическое среднее двух чисел а, b, равное , называется также средним пропорциональным между а и b.
I ж.
1. Раздел математики, изучающий пространственные формы и способы их измерения.
2. Учебный предмет, содержащий теоретические основы данного раздела математики.
3. разг.
Учебник, излагающий содержание данного учебного предмета.
II ж.
Очертания, контуры чего-либо.
ГЕОМЕ́ТРИЯ, геометрии, мн. нет, жен. (от греч. ge - земля и metreo - измеряю). Отдел математики, в котором изучаются пространственные формы, их измерение и взаимное расположение. Элементарная геометрия. Аналитическая геометрия (пользующаяся методами алгебры и анализа). Начертательная геометрия (занимающаяся решением геометрических задач в пространстве при помощи проектирования на плоскость).
ГЕОМЕ́ТРИЯ, -и, жен. Раздел математики, изучающий пространственные отношения и формы.
| прил. геометрический, -ая, -ое.
Геометрия
-и, только ед., ж.
Раздел математики, в котором изучаются пространственные отношения, формы и их обобщения.
Начертательная геометрия.
Задача по геометрии.
Кроме арифметики, Малевич преподавал мне также геометрию и алгебру (Ковалевская).
Родственные слова:
гео́метр, геометри́ческий
Этимология:
Заимствовано древнерусским языком из греческого (geōmetria ‘измерение земли’ ← gē ‘земля’ и metreō ‘мерю’).
Энциклопедический комментарий:
Возникновение геометрии относится к глубокой древности и было обусловлено практическими потребностями измерения земельных участков, объемов и пр. Строгое построение геометрии как системы теорем, последовательно выводимых из немногочисленных определений, основных понятий и истин, принимаемых без доказательства, было дано в Древней Греции. Такое изложение геометрии в "Началах" Евклида (ок. 300 г. до н. э.) в течение почти двух тысячелетий служило образцом применения аксиоматического метода и основой построения т. н. евклидовой геометрии. В 1826 г. Н. И. Лобачевский построил т. н. геометрию Лобачевского, отличающуюся от евклидовой аксиомой о параллельных прямых. В середине XIX в. были рассмотрены многомерные пространства. Некоторый принцип построения различных обобщений понятия пространства был дан Ф. Клейном (1872 г.). Обширная область геометрии - риманова геометрия - была заложена во второй половине XIX в. в работах Б. Римана. Геометрия применяется в самых различных областях не только математики, но и других наук.
ГЕОМЕ́ТРИЯ, -и, ж
Раздел математики, изучающий пространственные отношения (например, взаимное расположение) и формы (например, геометрические тела).
Профессор Д. М. Синцов вел семинар по геометрии, предметом которого было современное понятие о кривой линии в связи с развитием понятия о функции (Журн.).
ГЕОМЕ́ТРИЯ -и; ж. [греч. gē - Земля и metreō - измеряю]. Раздел математики, изучающий пространственные формы и отношения. // Учебный предмет, излагающий этот раздел математики. Урок геометрии. Преподаватель геометрии. // Разг. Учебник по этому предмету.
* * *
геоме́трия (от гео... и ...метрия), раздел математики, в котором изучаются пространственные отношения (например, взаимное расположение) и формы (например, геометрического тела) и их обобщения. Возникновение геометрии относится к глубокой древности и обусловлено практическими потребностями измерения земельных участков, объёмов и др. Строгое построение геометрии как системы предложений (теорем), последовательно выводимых из немногочисленных определений основных понятий и истин, принимаемых без доказательства (аксиом), было дано в Древней Греции. Такое изложение геометрии в «Началах» Евклида (около 300 до н. э.) в течение почти 2 тысяч лет служило образцом применения аксиоматического метода и основного построения так называемой евклидовой геометрии. Возрождение наук и искусств в Европе стимулировало развитие геометрии: теоретической основой построения изображений явилась проективная геометрия. Р. Декарт предложил метод координат, позволивший связать геометрию с алгеброй и математическим анализом, что породило аналитическую геометрию и дифференциальную геометрию. В 1826 Н. И. Лобачевский построил так называемую Лобачевского геометрию, отличающуюся от евклидовой аксиомой (постулатом) о параллельных. В середине XIX в. были рассмотрены многомерные пространства. Некоторый общий принцип построения различных обобщений понятия пространства (и соответствующих им геометрий) на основе теории групп преобразований был дан Ф. Клейном (1872). Обширная область геометрии - риманова геометрия - была заложена во второй половине XIX в. в работах Б. Римана. Обобщение основного предмета геометрии - пространства - привело к плодотворному применению геометрии в самых различных областях не только математики, но и других наук (физики, механики и др.).
* * *
ГЕОМЕТРИЯ - ГЕОМЕ́ТРИЯ (от гео- и греч. metreo - измеряю), раздел математики, в котором изучаются пространственные отношения (например, взаимное расположение) и формы (например, геометрические тела) и их обобщения. Возникновение геометрии относится к глубокой древности и обусловлено практическими потребностями измерения земельных участков, объемов и др. Строгое построение геометрии как системы предложений (теорем), последовательно выводимых из немногочисленных определений основных понятий и истин, принимаемых без доказательства (аксиом), было дано в Древней Греции. Такое изложение геометрии в «Началах» Евклида (около 300 до н. э.) в течение почти 2 тысяч лет служило образцом применения аксиоматического метода и основного построения евклидовой геометрии (см. ЕВКЛИДОВА ГЕОМЕТРИЯ). Возрождение наук и искусств в Европе стимулировало развитие геометрии: теоретической основой построения изображений явилась проективная геометрия (см. ПРОЕКТИВНАЯ ГЕОМЕТРИЯ). Р. Декарт предложил метод координат (см. КООРДИНАТЫ (в математике)), позволивший связать геометрию с алгеброй и математическим анализом, что породило аналитическую геометрию (см. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ) и дифференциальную геометрию (см. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ). В 1826 году Н. И. Лобачевский построил Лобачевского геометрию (см. ЛОБАЧЕВСКОГО ГЕОМЕТРИЯ), отличающуюся от евклидовой аксиомой (постулатом) о параллельных. В середине 19 века были рассмотрены многомерные пространства (см. МНОГОМЕРНОЕ ПРОСТРАНСТВО). Некоторый общий принцип построения различных обобщенных понятий пространства (и соответствующих им геометрий) на основе теории групп преобразований был дан Ф. Клейном (1872). Обширная область геометрии - риманова геометрия (см. РИМАНОВА ГЕОМЕТРИЯ) - была заложена во второй половине 19 века в работах Б. Римана. Обобщение основного предмета геометрии - пространства - привело к плодотворному применению геометрии в самых различных областях не только математики, но и других наук (физики, механики).
ГЕОМЕТРИЯ (от гео... и ...метрия) - раздел математики, в котором изучаются пространственные отношения (напр., взаимное расположение) и формы (напр., геометрические тела) и их обобщения. Возникновение геометрии относится к глубокой древности и обусловлено практическими потребностями измерения земельных участков, объемов и др. Строгое построение геометрии как системы предложений (теорем), последовательно выводимых из немногочисленных определений основных понятий и истин, принимаемых без доказательства (аксиом), было дано в Др. Греции. Такое изложение геометрии в "Началах" Евклида (ок. 300 до н. э. ) в течение почти 2 тыс. лет служило образцом применения аксиоматического метода и основного построения т. н. евклидовой геометрии. Возрождение наук и искусств в Европе стимулировало развитие геометрии: теоретической основой построения изображений явилась проективная геометрия. Р. Декарт предложил метод координат, позволивший связать геометрию с алгеброй и математическим анализом, что породило аналитическую геометрию и дифференциальную геометрию. В 1826 Н. И. Лобачевский построил т. н. Лобачевского геометрию, отличающуюся от евклидовой аксиомой (постулатом) о параллельных. В сер. 19 в. были рассмотрены многомерные пространства. Некоторый общий принцип построения различных обобщенных понятий пространства (и соответствующих им геометрий) на основе теории групп преобразований был дан Ф. Клейном (1872). Обширная область геометрии - риманова геометрия - была заложена во 2-й пол. 19 в. в работах Б. Римана. Обобщение основного предмета геометрии - пространства - привело к плодотворному применению геометрии в самых различных областях не только математики, но и других наук (физики, механики и др.).
ГЕОМЕТРИЯ - раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В планиметрии рассматриваются фигуры на плоскости; в стереометрии изучаются пространственные фигуры.
ИСТОРИЯ
Египет. Если не учитывать весьма скромный вклад древних обитателей долины между Тигром и Евфратом и Малой Азии, то геометрия зародилась в Древнем Египте до 1700 до н.э. Во время сезона тропических дождей Нил пополнял свои запасы воды и разливался. Вода покрывала участки обработанной земли, и в целях налогообложения нужно было установить, сколько земли потеряно. Землемеры использовали в качестве измерительного инструмента туго натянутую веревку. Еще одним стимулом накопления геометрических знаний египтянами стали такие виды их деятельности, как возведение пирамид и изобразительное искусство. Основным источником наших знаний о древнеегипетской геометрии является относящийся примерно к 1700 до н.э. папирус Ринда, названный по имени владельца, египтолога Ринда (этот папирус также называется папирусом Ахмеса) и хранящийся ныне в Лондоне в Британском музее. Папирус Ринда свидетельствует о том, что древних египтян интересовали главным образом практические аспекты геометрии и что при накоплении геометрических фактов египтяне почти всецело руководствовались интуицией, экспериментом и приближенными представлениями.
Греция. Около 600 до н.э. ионийские греки, совершившие путешествие в Египет, привезли на родину первые сведения о геометрии. Самым известным путешественником в Египет был Фалес (ок. 640 - ок. 546 до н.э.). Он был преуспевающим купцом, посвятившим последние годы жизни науке и политике. Фалес первым начал доказывать истинность геометрических соотношений, последовательно выводя их логически из некоторого набора общепринятых утверждений, называемых аксиомами или постулатами. Этот метод дедуктивного рассуждения, которому предстояло стать доминирующим в геометрии и фактически - во всей математике, сохраняет свое фундаментальное значение и в наши дни.
Одним из наиболее знаменитых учеников Фалеса был Пифагор (ок. 570 - ок. 500 до н.э.). Он много путешествовал, а потом поселился в Кротоне, в Италии, где основал общество, занимавшееся изучением арифметики, музыки, геометрии и астрономии. Пифагор и его последователи доказали много новых теорем о треугольниках, окружностях, пропорциях и некоторых трехмерных телах. Пифагор доказал также знаменитую теорему, носящую ныне его имя, согласно которой площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах. Пифагор умер в изгнании, но его влияние на греческих математиков ощущалось на протяжении многих веков. После его кончины в Элее (город в Италии) новыми центрами развивающейся геометрии становились по очереди Афины и Александрия. Архит Тарентский (ок. 428 - ок. 365 до н.э.) и Гиппий Элидский (р. ок. 425 до н.э.) затратили много усилий на решение трех задач, игравших важную роль в древнегреческой математике: это задачи о трисекции угла, о построении квадрата, площадь которого равна площади данного круга (задача о квадратуре круга), и о построении куба, имеющего вдвое больший объем, чем данный куб (задача об удвоении куба). Хотя ныне известно, что с помощью циркуля и линейки (единственных орудий геометрических построений, известных древнегреческим математикам) эти задачи решить нельзя, тем не менее попытки это сделать не были напрасны. Они стимулировали изучение конических сечений и способствовали совершенствованию математических методов.
Александрия. Афинская школа числила в своих рядах таких великих людей, как Платон и Аристотель. После смерти Аристотеля центр научной мысли переместился в Александрию (Египет), где в начале 3 в. до н.э. был основан знаменитый Александрийский Мусейон - один из главных научных центров античного мира. Живший в Александрии математик Евклид (3 в. до н.э.), биографические сведения о котором крайне скудны, собрал в 13 книгах своего сочинения значительную часть математических знаний того времени. Семь книг из 13 были посвящены геометрии, предмет которой был им тщательно и систематически изложен, различные утверждения и теоремы расположены в определенном порядке и перенумерованы. Была включена также теория пространственных тел, ограниченных плоскими поверхностями. Называлось это великое сочинение Начала, и последующие издания, точно придерживающиеся оригинала, стали основой обучения геометрии вплоть до нашего времени. Величайшим математиком античности был грек Архимед (ок. 287-212 до н.э.). Кроме множества других полученных им научных результатов и открытий, Архимед расширил ту часть Начал Евклида, в которой рассматривались пространственные тела, включив в их число сферу, цилиндр и конус. Другими великими александрийскими геометрами были Аполлоний Пергский (3 в. до н.э.; конические сечения), Птолемей (2 в. н.э.; астрономия) и Папп (3 в. н.э.; плоские кривые высших порядков). В 641 н.э. арабы разграбили Александрию и разрушили Мусейон и его библиотеку. Впрочем, греческая математика вступила в период застоя еще в начале 4 в. н.э, после кончины Паппа.
Средневековье. После падения Александрии большинство работ древнегреческих математиков были рассеяны или утрачены. Некоторые из них, в том числе Начала Евклида, были переведены и изучались арабами и индийцами. И хотя эти народы породили нескольких великих математиков, среди которых наиболее известны индийские математики Ариабхата (ок. 476 - ок. 550) и Бхаскара II (ок. 1114-1185), все же их самой большой заслугой следует считать сохранение геометрии в период Средневековья. После падения Римской империи в 5 в. наука в Европе долгое время находилась почти в полном забвении. В 12 и 13 вв. Начала были переведены с греческого и арабского на латынь и современные европейские языки, а геометрия вошла в программу монастырских школ. Первый из этих переводов был выполнен Аделардом Батским в 1120.
Новое время. За последние 300 лет доказательная геометрия была существенно расширена, а по своим методам и степени общности результатов она стала заметно отличаться от элементарной геометрии (т.е. геометрии, изложенной в Началах). Французский математик Ж.Дезарг (1593-1662) в связи с развитием учения о перспективе занялся исследованием свойств геометрических фигур в зависимости от их проекций. Тем самым он заложил основу проективной геометрии, которая изучает те свойства фигур, которые остаются неизменными при различных проекциях. В 19 в. это направление получило существенное развитие. Проективная геометрия, конические сечения и новая геометрия треугольников и окружностей составили содержание современной т.н. чистой геометрии. Тесно связанная с проективной, начертательная геометрия была введена французским математиком Г. Монжем (1746-1818). Эта новая область геометрии была связана с представлением изображений геометрических фигур на плоскости и определением геометрическими средствами расстояний, углов и линий пересечения. Начертательная геометрия представляет собой основу технического черчения. В 1637 Р. Декарт (1596-1650), французский философ и математик, опубликовал свою Геометрию - первый труд по аналитической геометрии, позволивший применить в геометрии мощные алгебраические методы. Геометрические задачи всех видов теперь могли решаться в рамках единого подхода; кроме того, благодаря новым методам стала возможной постановка и решение новых задач, о которых древние не могли даже помыслить, но которые ныне находятся в самом центре математики и математической физики. Со времен первого появления Начал математики тщетно пытались доказать пятый постулат Евклида: через точку, не лежащую на прямой, можно провести только одну прямую, ей параллельную. В 19 в. было доказано, что можно построить непротиворечивую геометрию, используя все аксиомы и постулаты Евклида и отрицание постулата о параллельных, а это означало, что искомого доказательства пятого постулата не существует. Любая такая непротиворечивая геометрия получила название неевклидовой геометрии. Около 1830 Я.Бойяи (1802-1860) и Н.И.Лобачевский (1792-1856) независимо друг от друга построили геометрию, использовавшую постулат, согласно которому через точку, лежащую вне прямой, можно провести много прямых, ей параллельных. В 1854 Б.Риман (1826-1866) сформулировал постулат, согласно которому через точку вне прямой невозможно провести ни одной параллельной, что дало начало т.н. римановой геометрии. Неевклидова математика расширилась и стала включать в себя тригонометрию, аналитическую и дифференциальную геометрии, охватив не только планиметрию, но и стереометрию, а также геометрию пространств размерности больше трех (геометрию гиперпространств). Евклидова и обе неевклидовы геометрии одинаково хорошо служат для описания той ограниченной области пространства, в которой мы живем, хотя геометрия Евклида проще по форме. В то же время при переходе к римановой геометрии некоторые современные физические теории существенно упрощаются.
ЭЛЕМЕНТАРНАЯ ПЛАНИМЕТРИЯ
Аксиомы и постулаты. Существует набор исходных посылок, называемых аксиомами и постулатами, на которых базируется вся структура геометрии.
Аксиомы. Аксиомы - это утверждения, принимаемые за истинные без доказательств. Аксиомы обычно подразделяются на две группы: общие, относящиеся ко всей математике, и геометрические. К числу общих аксиом относятся следующие.
1. Равные одному и тому же равны между собой. 2. Если к равным прибавляются равные, то суммы будут равны. 3. Если от равных отнимаются равные, то остатки будут равны. 4. Если равные умножить на равные, то произведения будут равны. 5. Если равные разделить на равные, то частные будут равны. Деление на нуль запрещается. 6. Одинаковые степени равных, а также корни одинаковой степени из равных равны. 7. Целое больше любой своей части. 8. Целое равно сумме своих частей.
К числу геометрических аксиом относятся следующие.
1. Через любые две данные точки можно провести только одну прямую. 2. Геометрическую фигуру можно перемещать в пространстве, не изменяя ни ее размеров, ни ее формы. 3. Геометрические фигуры, которые совпадают после наложения, конгруэнтны (т.е. равны). 4. Прямая есть кратчайшее расстояние между двумя точками.
Постулаты. Следующие постулаты касаются построений и принимаются за истинные без доказательств.
1. Через любые две данные точки можно провести прямую. 2. Прямая может быть продолжена бесконечно или же ограничена в любой своей точке. 3. Окружность может быть описана вокруг любой данной точки как центра и с любым радиусом. 4. Все прямые углы равны. 5. Через точку, не лежащую на прямой, можно провести одну и только одну прямую, ей параллельную.
Некоторые геометрические фигуры, построения и заключения. Многие термины, используемые для описания фигур в геометрии, настолько фундаментальны, что определить их не представляется возможным. Все попытки сделать это приводили лишь к замене одних терминов другими, столь же неопределимыми, или к простому описанию некоторых свойств фигур. Например, термин "точка" не поддается определению.
Линии. Термин "линия" (или "кривая" в широком смысле слова) не имеет определения, хотя мысленно линию можно представить как след движущейся точки. Бесчисленные попытки определить прямую линию (рис. 1,а) не имели успеха. Многие из этих попыток апеллировали к физическому эксперименту, например, "прямая - это туго натянутая линия". Чаще других приводится описание прямой, предложенное Архимедом: "Прямая - это кратчайшее расстояние между двумя точками". Это "определение", однако, лишь заменяет неопределяемое понятие прямизны столь же неопределяемым понятием расстояния. Предполагается, что прямая бесконечна, т.е. ее можно неограниченно продолжить в обе стороны. Часть прямой называется отрезком. Ломаная (рис. 1,б) состоит из прямолинейных отрезков. Кривой (рис. 1,в) называется линия, никакая часть которой не является прямой.
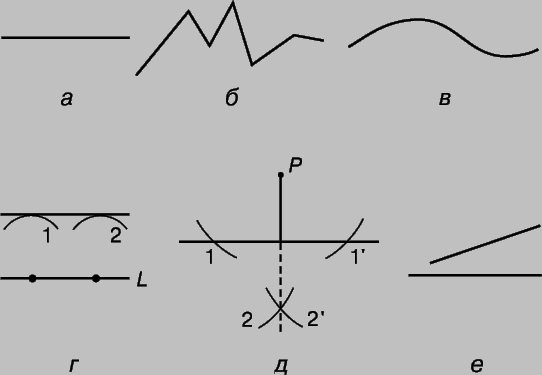
Рис. 1. ЛИНИИ. а - прямая; б - ломаная; в - гладкая кривая; г - параллельные прямые; д - перпендикулярные прямые; е - наклонные прямые.
Как показано на рис. 1,г, 1,д и 1,е, прямые могут быть параллельными, перпендикулярными и наклонными. Параллельные прямые - это прямые, расстояние между которыми всюду одинаково. На рис. 1,г показано, как построить прямую, параллельную данной прямой L и отстоящую от нее на заданное расстояние. Берется окружность, радиус которой равен данному расстоянию. Проводятся две дуги с центрами в двух различных точках прямой L. Прямая, касательная к обеим дугам, и есть та прямая, которую требовалось построить. На рис. 1,д показано, как построить прямую, проходящую через точку Р и перпендикулярную прямой L. Порядок, в котором делаются засечки дугами, указаны номерами [[первыми следует провести (в любой последовательности) либо дугу 1, либо дугу 1']]. Для проведения дуг 2 и 2' циркуль устанавливается в точки пересечения прямой L дугами 1 и 1' соответственно, радиусы остаются те же самые. Прямая, проходящая через точку Р и точку пересечения дуг 2 и 2', есть искомый перпендикуляр. Перпендикуляр - это кратчайшая линия, которую можно провести от точки до прямой, на которую он опущен, и расстояние от точки до прямой по определению равно длине перпендикуляра, опущенного из нее на прямую.
Углы. Углом называется фигура, образованная двумя полупрямыми, исходящими из одной точки. Эта точка называется вершиной угла, а полупрямые - сторонами угла. Если стороны угла перпендикулярны друг другу, то образуемый ими угол называется прямым (рис. 2,а). Углы меньше прямого называются острыми (рис. 2,б), а углы больше прямого - тупыми (рис. 2,в). Развернутым называется угол, обе стороны которого лежат на одной прямой (рис. 2,г); такой угол равен двум прямым углам. Биссектрисой угла называется прямая, проходящая через его вершину и делящая угол пополам. Углы можно измерять количественно, если определить единицу измерения угла (угол в один градус) как 1/180 развернутого угла. Таким образом, прямой угол содержит 90°, а угол на рис. 2,д содержит больше 180°, но меньше 360°.
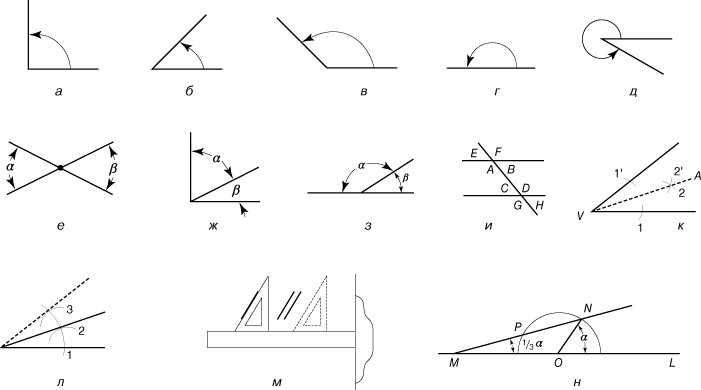
Рис. 2. УГЛЫ. а - прямой угол; б - острый угол; в - тупой угол; г - развернутый угол; д - угол, больший 180° и меньший 360°; е - вертикальные углы; ж - дополнительные углы (до 90°); з - смежные углы (до 180°); и - углы, образованные при пересечении параллельных прямой; к - деление угла пополам; л - удвоение угла; м - вычерчивание параллельных с помощью треугольника и рейсшины; н - трисекция угла по Архимеду.
На рис. 2,е, 2,ж, 2,з и 2,и показано, как соотносятся между собой углы некоторых фигур. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого (рис. 2,е). Вертикальные углы равны. Дополнительные углы в сумме составляют 90° (рис. 2,ж), а смежные углы в сумме дают 180° (рис. 2,з). Если прямая пересекает две параллельные прямые, как на рис. 2,и, то углы E, B, C и H равны, и углы F, A, D и G также равны между собой. Углы между параллельными (углы А, В, С, D на рисунке) называются внутренними, а углы, лежащие вне параллельных - внешними. Тот факт, что параллельные образуют с пересекающей их прямой равные углы, используется при вычерчивании параллельных прямых (рис. 2,м). На рис. 2,к показано, как с помощью циркуля и линейки разделить пополам данный угол: прямая VA - биссектриса угла. На рис. 2,л показано, как удвоить данный угол. Традиционно в элементарной геометрии выполнялись лишь геометрические построения, которые можно осуществить, используя только циркуль и линейку без делений. Общего подхода к таким построениям не существует, и успех почти целиком зависит от настойчивости и изобретательности. Так, например, может показаться, что задача о разделении угла на три равные части, т.н. трисекция угла, достаточно легка, поскольку сходная с ней задача деления угла пополам решается довольно просто. Однако на протяжении веков все усилия как любителей, так и профессионалов осуществить трисекцию угла неизменно оканчивались неудачей. Правда, эту задачу удалось решить, используя некоторые плоские кривые высших порядков, например, конхоиду и квадратриссу, а Архимед показал, как можно было бы решить задачу о трисекции угла с помощью линейки с двумя отметинами (рис. 2,н). В предложенном им решении задачи на ребре линейки откладывается расстояние МР, равное радиусу ON. Линейка кладется так, чтобы ее край проходил через точку N, тогда точка М попадает на продолжение прямой OL, а точка P - на окружность. Задача о трисекции угла эквивалентна поиску геометрического построения, позволяющего находить корни уравнения x3 - 2 = 0. В 1837 вопрос о трисекции был окончательно решен французским математиком П.Ванцелем, давшим строгое доказательство невозможности точной трисекции угла в общем случае с помощью циркуля и линейки.
Треугольники. Треугольником называется плоская фигура, ограниченная тремя прямыми. У треугольника могут быть три неравные стороны (разносторонний треугольник), две равные стороны (равнобедренный треугольник) или три равные стороны (равносторонний треугольник) (рис. 3,а, 3,б, 3,в). В равнобедренном треугольнике углы, лежащие против равных сторон (углы a и b на рис. 3,б), равны; в равностороннем треугольнике все углы равны.
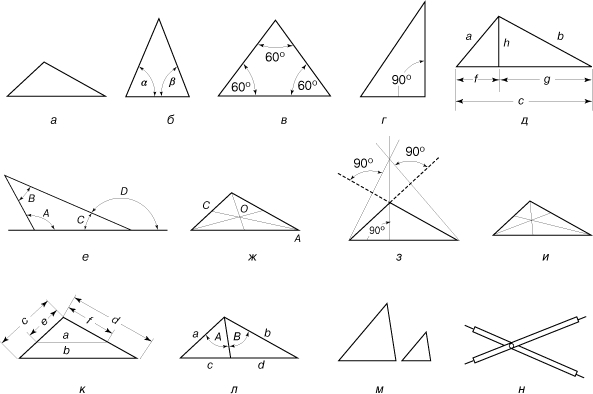
Рис. 3. ТРЕУГОЛЬНИКИ. а - разносторонний; б - равнобедренный; в - равносторонний; г - прямоугольный; д - длины сторон и отрезков в прямоугольном треугольнике; е - углы треугольника; ж - медианы; з - высоты; и - биссектрисы углов; к - треугольник, рассеченный прямой, параллельной одной из сторон; л - треугольник, рассеченный биссектрисой одного из углов; м - подобные треугольники; н - пропорциональный делитель.
Прямоугольным называется треугольник (рис. 3,г), у которого один из углов прямой. Сторона, лежащая против прямого угла, называется гипотенузой; две стороны, образующие прямой угол, называются катетами. Некоторые соотношения между длинами сторон прямоугольного треугольника мы приведем в обозначениях, указанных на рис. 3,д. Знаменитая теорема Пифагора гласит; квадрат длины гипотенузы в прямоугольном треугольнике равен сумме квадратов длин катетов, или c2 = a2 + b2. Длина перпендикуляра h, опущенного из вершины прямого угла на гипотенузу, есть среднее пропорциональное длин отрезков, на которые основание перпендикуляра делит гипотенузу:
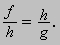
Углы внутри треугольника называются внутренними; углы, которые образуются, если стороны треугольника продлить за их вершины, называются внешними (рис. 3,е). Сумма внутренних углов треугольника равна развернутому углу. Любой внешний угол равен сумме двух внутренних углов, не имеющих с ним общей вершины (РD = РA + РB). Отрезок прямой, соединяющий вершину треугольника с серединой противолежащей стороны, называется медианой. Три медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины. Например, на рис. 3,ж отрезок АО составляет 2/3 от длины отрезка АС. Точка пересечения медиан является также центром тяжести треугольника (треугольник, вырезанный из однородного по толщине и плотности материала и подвешенный в этой точке, будет находиться в равновесии). Высотой треугольника называется перпендикуляр, опущенный из одной из его вершин на противоположную сторону (или ее продолжение). Все три высоты треугольника пересекаются в одной точке, которая называется ортоцентром (рис. 3,з); биссектрисы всех углов треугольника также пересекаются в одной точке, которая является центром вписанной окружности (рис. 3,и) и равноудалена от всех сторон треугольника. Прямая, пересекающая треугольник и параллельная одной из его сторон, делит две другие стороны на пропорциональные отрезки. На рис. 3,к a/b = e/c = f/d. Биссектриса любого угла треугольника делит противоположную сторону на отрезки, пропорциональные длинам сторон, образующих угол. На рис. 3,л, если РA = РB, то c/a = d/b. Два треугольника (любые фигуры) называются равными (или конгруэнтными), если они переводятся друг в друга преобразованиями движения. Преобразование одной фигуры в другую называется движением, если оно сохраняет расстояния между точками. Можно доказать три признака равенства треугольников: два треугольника равны, если 1) две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника; 2) сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ним углам другого треугольника; и 3) три стороны одного треугольника равны соответственно трем сторонам другого треугольника. Если треугольники можно перевести друг в друга преобразованием движения, не выводящим их из плоскости, в которой оба они лежат, то они называются собственно конгруэнтными; если же один из треугольников необходимо перевернуть, то треугольники называются несобственно конгруэнтными. Преобразование одной фигуры в другую называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одно и то же число раз. Две фигуры подобны, если они переводятся друг в друга преобразованием подобия. Если два треугольника подобны (рис. 3,м), то их углы равны, а соответствующие стороны пропорциональны. Пропорциональным делителем, изображенным на рис. 3,н, пользуются для того, чтобы увеличить или уменьшить чертеж в требуемое число раз. Площадь любого треугольника равна половине произведения его стороны на проведенную в ней высоту:
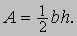
Если треугольник равносторонний, то его площадь равна
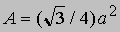
, где а - длина стороны. Если а, b, c - длины сторон треугольника, то его площадь определяется по формуле
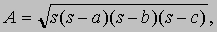
вывод которой приписывают Герону (s - полупериметр).
Четырехугольники. Четырехугольником является всякая плоская фигура, ограниченная четырьмя прямыми (рис. 4). Параллелограммом называется четырехугольник, у которого противоположные стороны имеют равную длину. Ромб (рис. 4,г) - это параллелограмм, все стороны которого равны, а прямоугольник (рис. 4,д) - это параллелограмм, у которого все углы прямые. Диагонали параллелограмма (рис. 4,ж) в точке пересечения делятся пополам; в прямоугольнике диагонали равны. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие - непараллельны. Параллельные стороны называются основаниями. Площадь трапеции равна произведению высоты на полусумму ее оснований: A = h [[(b + d)/2]]. Площадь параллелограмма A = bh. Один из методов определения площади четырехугольника состоит в разбиении фигуры на два треугольника с помощью диагонали и в вычислении суммы площадей образовавшихся треугольников.
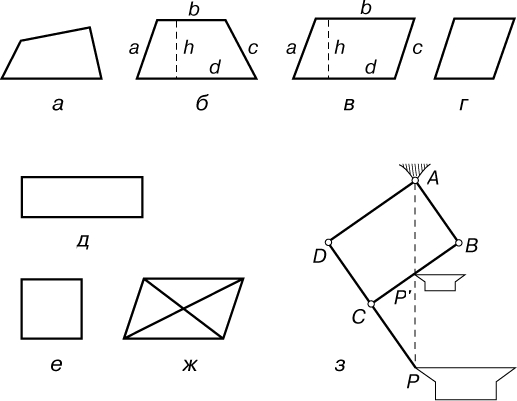
Рис. 4. ЧЕТЫРЕХУГОЛЬНИКИ. а - четырехугольник, у которого никакие стороны не параллельны; б - трапеция; в - параллелограмм; г - ромб; д - прямоугольник; е - квадрат; ж - диагонали параллелограмма; з - пантограф.
Интересным приложением свойств параллелограмма служит шарнирный пантограф (рис. 4,з), используемый для перечерчивания чертежей и других графических изображений в большем или меньшем масштабе. Пантограф представляет собой шарнирный механизм, имеющий форму параллелограмма, закрепленный в вершине А, со звеном DC, продленным до точки Р. Прямая РА пересекает звено СВ в точке Р'. Звено СВ всегда параллельно звену DA, следовательно, треугольники PDA и PCP' подобны. Поэтому CP' = DAЧPC/PD, а эта величина постоянна, поэтому точка Р' звена СВ также лежит на прямой, соединяющей точки Р и А. Из двух рассмотренных выше подобных треугольников следует, что отношение РА/Р'А также постоянно. Следовательно, в любом положении пантографа перемещение точки Р' пропорционально перемещению точки Р. Если точка Р движется по контуру какой-либо фигуры, то точка Р', в которой находится острие карандаша, повторяет без искажений этот контур в уменьшенном масштабе. Отношение масштабов оригинала и копии равно РА/Р'А = PD/CD.
Многоугольники. Многоугольником называется плоская фигура, ограниченная замкнутой ломаной линией, звенья которой называются сторонами. Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону. Выпуклый многоугольник называется правильным, если все стороны и углы его равны. Расстояние от центра правильного многоугольника до какой-либо его стороны равно радиусу вписанной в него окружности (обозначен на рис. 5,а буквой а). Площадь правильного многоугольника равна произведению половины радиуса на периметр:
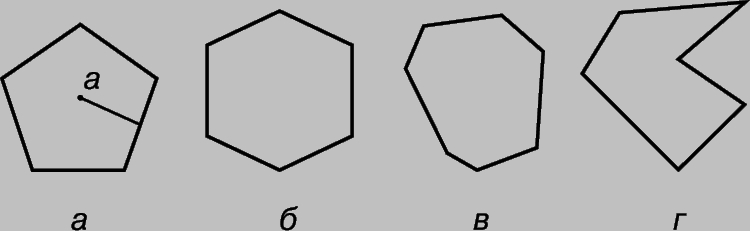
Рис. 5. ОБРАЗЦЫ МНОГОУГОЛЬНИКОВ. а - правильный пятиугольник; б - правильный шестиугольник; в - неправильный семиугольник; г - вогнутый многоугольник.
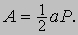
В табл. 1 приведены названия и формулы для площадей некоторых правильных многоугольников (s означает длину стороны).
Древние греки научились строить правильные многоугольники с 3, 4, 5, 6, 8, 10 и 15 сторонами. И сами греки, и многие после них безуспешно пытались разработать методы построения других многоугольников. В 1796 К.Гаусс, которому тогда было всего 19 лет, обнаружил, что правильный многоугольник можно построить с помощью циркуля и линейки только в том случае, если число сторон n равно простому числу вида или произведению простых чисел такого вида. В этой формуле t - любое целое число. Таким образом, построение с помощью циркуля и линейки правильных 7-, 9-, 11- и 13-угольников невозможно. Гаусс построил правильный 17-угольник, и из его работы следовало, что могут быть построены правильные 257-угольник и 65537-угольник.
Окружность. Окружностью называется замкнутая плоская кривая, все точки которой одинаково удалены от данной точки, называемой центром и лежащей в той же плоскости, что и кривая. Через три точки, не лежащие на одной прямой, можно провести только одну окружность. Часть плоскости, ограниченная окружностью, называется кругом. Различные термины, используемые при изучении окружности, представлены на рис. 6,а и 6,б.
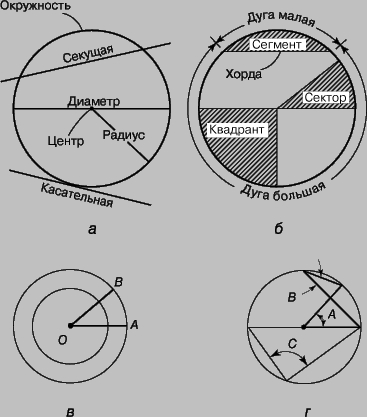
Рис. 6. ОКРУЖНОСТЬ. а и б - элементы окружности; в - концентрические окружности; г - вписанные углы.
Концентрическими называются окружности, имеющие общий центр (рис. 6,в). Угол называется центральным углом окружности, если его вершина совпадает с центром окружности, а стороны - с ее радиусами. Например, угол АОВ на рис. 6,в - центральный угол обеих концентрических окружностей. Окружность делится на 360 равных долей, и число градусов в центральном угле, опирающемся на дугу окружности, равно числу 1/360 долей окружности, укладывающихся в этой дуге. На рис. 6,г А - центральный угол, а В - вписанный угол (т.е. угол, вершина которого лежит на окружности), опирающийся на ту же дугу окружности, что и центральный угол А. Согласно одной из теорем геометрии вписанный угол измеряется половиной дуги, на которую он опирается. Например,
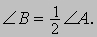
Следовательно, вписанный угол С, опирающийся на половину окружности, - прямой. Площадь круга равна четверти произведения длины его окружности на диаметр. Отношение длины окружности к диаметру приближенно равно 3,14159265 (Пи); площадь круга можно также записать в виде A = p r2, где r - радиус. История точного определения числа p (читается "пи") очень интересна сама по себе. В 1882 немецкий математик Ф.Линдеман (1852-1939) доказал, что древняя проблема квадратуры круга, геометрически эквивалентная построению отрезка неразрешима, так как число p не удовлетворяет никакому алгебраическому уравнению с целыми коэффициентами. Примеры элементарных геометрических доказательств. Утверждения элементарной геометрии распадаются на две группы: на теоремы, в которых доказательство утверждения предъявляется в явном виде, и задачи, в которых излагается способ построения, а затем проверяется его правильность. В качестве примера теоремы рассмотрим следующее доказательство. Утверждение: в равнобедренном треугольнике углы, лежащие против равных стороны, равны. Дано: треугольник АВС с равными сторонами АВ и АС. Требуется доказать: РB = РC.
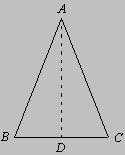
Рассмотрим пример задачи на построение. Задача: построить правильный шестиугольник, вписанный в окружность. Дано: Окружность с центром О.
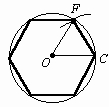
СТЕРЕОМЕТРИЯ
Плоскость. Плоскость (рис. 7,а) определяется: 1) тремя точками; 2) двумя пересекающимися прямыми; 3) двумя параллельными прямыми; и 4) прямой и точкой, лежащей вне ее. Прямые, которые не пересекаются и не лежат в одной плоскости, называются скрещивающимися. На рис. 7,б изображены две параллельные плоскости А и В. Если пересечь их третьей плоскостью С, то линии пересечения будут параллельны.
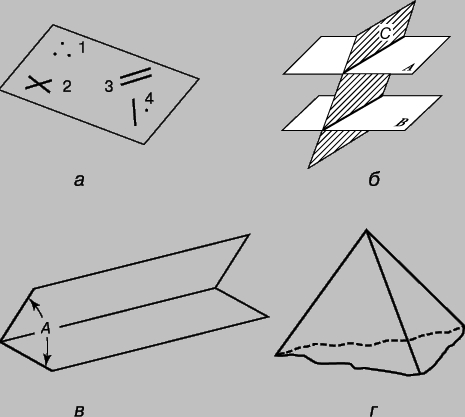
Рис. 7. ПЛОСКОСТИ. а - задание плоскости; б - параллельные плоскости, пересеченные третьей плоскостью; в - двугранный угол; г - трехгранный угол.
Двугранным углом называется фигура, образованная двумя полуплоскостями с общей ограничивающей их прямой. Его величина измеряется углом, полученным от пересечения этих плоскостей плоскостью, перпендикулярной к ним (рис. 7,в). Фигура, образованная тремя или более плоскостями, которые пересекаются в одной точке, называется многогранным углом (рис. 7,г).
Многогранник. Это фигура, ограниченная со всех сторон плоскими многоугольниками, называемыми гранями. Многогранник называется выпуклым, если он расположен по одну сторону плоскости. Декарт и Эйлер доказали, что любой выпуклый многогранник обладает замечательным свойством, состоящим в том, что сумма числа его граней и вершин равна числу его ребер плюс два. Если все грани выпуклого многогранника - конгруэнтные правильные многоугольники, то многогранник называется правильным.
Призма. Призмой (рис. 8) называется многогранник, у которого две грани лежат в параллельных плоскостях и имеют форму конгруэнтных многоугольников, а остальные грани имеют форму параллелограммов. Параллелепипед (рис. 8,в) - это призма, основаниями которой служат параллелограммы. Площадь боковой поверхности любой призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра. Объем равен произведению площади основания на высоту.
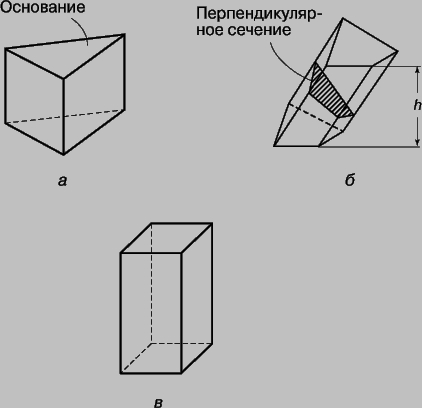
Рис. 8. ПРИЗМЫ. а - прямая треугольная призма; б - наклонная призма; в - прямоугольный параллелепипед.
Пирамида. Пирамидой (рис. 9) называется многогранник, основанием которого служит плоский многоугольник, а боковые грани имеют форму треугольников с общей вершиной. Площадь боковой поверхности правильной прямой пирамиды равна 1/2 произведения периметра основания на высоту боковой грани s (рис. 9). Объем любой пирамиды равен 1/3 произведения площади основания на высоту h.
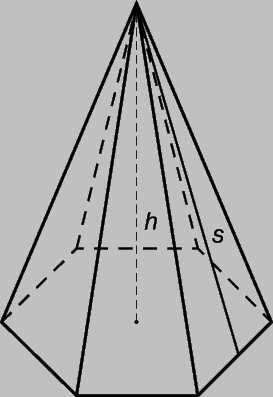
Рис. 9. ПРЯМАЯ ПРАВИЛЬНАЯ ПИРАМИДА.
Цилиндр и конус. Цилиндром (или цилиндрической поверхностью) (рис. 10,а) называется поверхность, порожденная прямой Е, называемой образующей, которая движется параллельно самой себе по некоторой фиксированной кривой D, называемой директрисой. Если образующая, двигаясь по директрисе, всегда проходит через одну и ту же точку А, называемую вершиной (рис. 10,г), то получаемая в результате движения поверхность называется конусом. Призма - частный случай цилиндра, а пирамида - частный случай конуса. Формулы для площадей боковой поверхности и объемов призмы и пирамиды применимы, соответственно, к цилиндру и конусу.
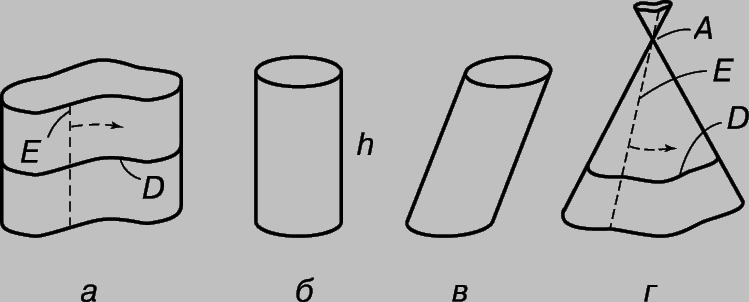
Рис. 10. ЦИЛИНДРЫ И КОНУСЫ. а - образующая цилиндра; б - прямой круговой цилиндр; в - наклонный круговой цилиндр; г - образующая конуса.
Сфера. Сферой называется замкнутая поверхность, все точки которой равноудалены от одной точки, называемой центром. Если плоскость пересекает сферу, то линия пересечения имеет форму окружности. Наибольшая окружность (называемая большим кругом) получается, когда секущая плоскость проходит через центр сферы. Параллели, соответствующие различным широтам, - малые круги Земли, экватор и все меридианы - большие круги. Часть пространства, ограниченная сферой и содержащая ее центр, называется шаром. Площадь поверхности сферы равна A = 4p r2, объем шара
ГЕОМЕТРИЯ (от гео... и ...метрия), часть математики, изучающая пространственные формы (например, фигуры и тела), их отношения (например, взаимное расположение) и их обобщения. Зарождение геометрии относится ко 2-му тысячелетию до нашей эры, в самостоятельную отрасль математики сформировалась в 4 - 3 вв. до нашей эры.
геоме́трия, геоме́трии, геоме́трий, геоме́триям, геоме́трию, геоме́трией, геоме́триею, геоме́триями, геоме́триях
сущ., кол-во синонимов: 9
астероид (579)
линиолонгиметрия (2)
линиометрия (2)
лонгиметрия (1)
математика (29)
микрогеометрия (1)
планиметрия (2)
психогеометрия (1)
стереометрия (2)
Др.-рус. заимств. из греч. яз., в котором geōmetria - сложносуффиксальное образование на базе gē «земля» и metreō «мерить».
геоме́трия
геоме́тр, геометрист (в эпоху Петра I; см. Смирнов 88). Первонач. через польск. geometria или прямо из лат. geometria; см. еще Горяев, ЭС 445 [у которого прямо из греч. - Ред.]; геометрист, возм., через польск. geometrysta.
ГЕОМЕТРИЯ (греч. geometria, от ge - земля, и metron - мера). Часть математики, имеющая предметом свойства и измерения линий, поверхностей и объемов тел.
- Треугольная наука.
- Раздел математики.
- Начертательная ...
- В каком разделе математики изучают теорему Пифагора?
- Раздел математики, изучающий пространственные формы и способы их измерения.
- Этой науке посвящался учебник «Землемерие радиксом и циркулем», составленный Елизарьевым в 1600 году.
- Одна из семи свободных наук.
- Понселе занимался проективной ею, а Монж - начертательной.
- Фильм Гильермо Дель Торо.