м.

Целая величина, рассматриваемая как сумма своих бесконечно малых частей (в математике).

ИНТЕГРА́Л, интеграла, муж. (от лат. integer - целый) (мат.). Конечная измеримая величина в отношении к бесконечно малой части ее - к диференциалу.

ИНТЕГРА́Л [тэ ], -а, муж. В математике: величина, получающаяся в результате действия, обратного дифференцированию.

| прил. интегральный, -ая, -ое. Интегральное исчисление.

ИНТЕГРАЛ - муж., мат., лат. конечная, измеримая величина, в отношении к бесконечно малой части ее, к дифференциалу. Интегральное вычисление, искусство отыскивать интеграл по дифференциалу. Интегрировать, вычислять, находить интеграл; интеграция жен. действие это.

ИНТЕГРА́Л [тэ], -а; м. [от лат. integer - целый] Матем. Величина, получающаяся в результате действия, обратного дифференцированию.

◁ Интегра́льный, -ая, -ое. И-ое исчисление (раздел математики, в котором изучаются свойства и способы вычисления интегралов и их приложения). И-ые уравнения (содержащие неизвестные функции под знаком интеграла).

* * *

интегра́л (от лат. integer - целый), см. Интегральное исчисление.

* * *

ИНТЕГРАЛ - ИНТЕГРА́Л (от лат. integer - целый), см. Интегральное исчисление (см. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ).

ИНТЕГРАЛ (от лат. integer - целый) - см. Интегральное исчисление.

-а, м. мат.

Величина, получающаяся в результате действия, обратного дифференцированию.

[От лат. integer - целый]

ИНТЕГРАЛ (от латинского integer - целый), одно из основных понятий интегрального исчисления.

интегра́л, -а

интегра́л [тэ]

интегра́л. Произносится [интэгра́л].

интегра́л, интегра́лы, интегра́ла, интегра́лов, интегра́лу, интегра́лам, интегра́лом, интегра́лами, интегра́ле, интегра́лах

сущ., кол-во синонимов: 2

первообразная, термин

интегр/а́л/.

интегра́л м 1a

Латинское - integralis, integer (целый, полный).

В русском языке слово «интеграл» как математический термин появилось в 50-70-х гг. XVIII в. из французского языка. Впервые его ввел в обиход швейцарский математик Я. Бернулли, опираясь на латинское существительное.

Производные: интегральный, интегрировать, интеграция.

Заимств. во второй половине XVIII в. из франц. яз., где оно является неологизмом швейцарского математика Я. Бернулли на базе лат. integralis, суф. производного от integer «целый, полный».

ИНТЕГРАЛ а, м. intégrale f. <лат. integer целый. Математическое понятие о целой величине как сумме своих бесконечно малых частей. Нахождение интеграла. БАС-1. Найти интеграл уравнения. 1766. Котельников Геодет 175. // Сл. 18. Алферинька недурно разложил в "серию" интеграл Эмилии Осиповны. Черн. Перл создания. // ПСС 12 186. Отец проверяет тетрадку сына: - Ты почему так неровно пишешь крючочки? - Это не крючочки, это интегралы. Крокодил 1994 9 11. || перен. Что же я заметил? - Во-первых, что управление губернское в интеграле идет несравненно лучше, нежели я думал. 1835. Герц. // 30-21 44. Скорость человеческой эволюции в данном направлении зависит от интеграла единичных воль. Кропоткин Зап. 251. Интегралист а, м. Наконец по контракту служили два француза: Ламе и Клаперон; первый - превосходный физик, механик, интегралист и вообще математик-теорист, а второй ветреная голова. Щук. сб. 4 256. - Лекс. САН 1847: интегра/л; Сл. 186 интеграл 1766.

ИНТЕГРАЛ (вово-лат., от лат. integer - ценный). В математике - количество, дифференциал которого равен данной величине.

- Математическая «загогулина».

- Величина, получающаяся в результате действия, обратного дифференцированию.

- Криволинейный в алгебре.

- Какой знак из математики стал символом бионики?

- F(x)+C, где F(x) - первообразная.

- Экс-группа Бари Алибасова.

Составить слова из слова интеграл

ИНТЕГРАЛИСТ а, м. intégrale adj., intégration f. Сторонник политической интеграции. В одном <лагере>- великодержавники, славянофилы и евразийцы, в другом - западники, интегралисты или космополиты. НС 1998 2 270.

Составить слова из слова интегралист

ИНТЕГРАЛЫ - новолатинск. Голландские государственный бумаги, которые принадлежат к совокупности государственных долгов, как дополнительная часть.

Составить слова из слова интегралы

ИНТЕГРАЛЫ или ИНТЕГРИРОВАННЫЕ (ново-лат.). Голландские государственные бумаги, которые принадлежат к совокупности государственных долгов, как дополнительная часть.

Составить слова из слова интегралы или интегрированные

Интегра́льная микросхе́ма - см. Интегральная схема.

* * *

ИНТЕГРАЛЬНАЯ МИКРОСХЕМА - ИНТЕГРА́ЛЬНАЯ МИКРОСХЕ́МА, см. Интегральная схема (см. ИНТЕГРАЛЬНАЯ СХЕМА).

ИНТЕГРАЛЬНАЯ МИКРОСХЕМА - см. Интегральная схема.

Составить слова из слова интегральная микросхема

ИНТЕГРАЛЬНАЯ МИКРОЭЛЕКТРОНИКА - ИНТЕГРА́ЛЬНАЯ МИКРОЭЛЕКТРО́НИКА, см. Микроэлектроника (см. МИКРОЭЛЕКТРОНИКА).

ИНТЕГРАЛЬНАЯ Микроэлектроника - см. Микроэлектроника.

Составить слова из слова интегральная микроэлектроника

Интегра́льная о́птика - раздел оптики, исследующий миниатюрные оптические системы, содержащие тонкоплёночные диэлектрические световоды (толщиной порядка длины световой волны), генераторы и другие элементы. Эти системы осуществляют преобразование, усиление и передачу световых сигналов, подобно электрическим сигналам в интегральных схемах.

* * *

ИНТЕГРАЛЬНАЯ ОПТИКА - ИНТЕГРА́ЛЬНАЯ О́ПТИКА, раздел оптики, исследующий миниатюрные оптические системы, содержащие тонкопленочные диэлектрические световоды (толщиной порядка длины световой волны), генераторы и другие элементы. Эти системы осуществляют преобразование, усиление и передачу световых сигналов, подобно электрическим сигналам в интегральных схемах (см. ИНТЕГРАЛЬНАЯ СХЕМА).

ИНТЕГРАЛЬНАЯ ОПТИКА - раздел оптики, исследующий миниатюрные оптические системы, содержащие тонкопленочные диэлектрические световоды (толщиной порядка длины световой волны), генераторы и другие элементы. Эти системы осуществляют преобразование, усиление и передачу световых сигналов, подобно электрическим сигналам в интегральных схемах.

Составить слова из слова интегральная оптика

Интегра́льная схе́ма (ИС, интегральная микросхема, микросхема), микроминиатюрное электронное устройство, элементы которого изготовлены в едином технологическом цикле и неразрывно связаны (объединены) конструктивно и электрически. Интегральные схемы подразделяются: по способу объединения (интеграции) элементов - на полупроводниковые, или монолитные (основной тип), плёночные и гибридные (в том числе многокристальные); по виду обрабатываемой информации - на цифровые и аналоговые; по степени интеграции элементов - на малые, интегральные схемы со средней степенью интеграции, большие (БИС) и сверхбольшие (СБИС).

* * *

ИНТЕГРАЛЬНАЯ СХЕМА - ИНТЕГРА́ЛЬНАЯ СХЕ́МА (ИС, интегральная микросхема, микросхема), микроминиатюрное электронное устройство, элементы которого неразрывно связаны (объединены) конструктивно, технологически и электрически. ИС подразделяются: по способу объединения (интеграции) элементов - на полупроводниковые, или монолитные (основной тип), пленочные и гибридные (в т. ч. многокристальные); по виду обрабатываемой информации - на цифровые и аналоговые; по степени интеграции элементов - на малые, ИС со средней степенью интеграции, большие (БИС) и сверхбольшие (СБИС). См. также Микроэлектроника (см. МИКРОЭЛЕКТРОНИКА).

ИНТЕГРАЛЬНАЯ СХЕМА (ИС - интегральная микросхема, микросхема), микроминиатюрное электронное устройство, элементы которого неразрывно связаны (объединены) конструктивно, технологически и электрически. ИС подразделяются: по способу объединения (интеграции) элементов - на полупроводниковые, или монолитные (основной тип), пленочные и гибридные (в т. ч. многокристальные); по виду обрабатываемой информации - на цифровые и аналоговые; по степени интеграции элементов - на малые, ИС со средней степенью интеграции, большие (БИС) и сверхбольшие (СБИС).

ИНТЕГРАЛЬНАЯ СХЕМА (ИС), микроэлектронная схема, сформированная на крошечной пластинке (кристаллике, или "чипе") полупроводникового материала, обычно кремния, которая используется для управления электрическим током и его усиления. Типичная ИС состоит из множества соединенных между собой микроэлектронных компонентов, таких, как транзисторы, резисторы, конденсаторы и диоды, изготовленные в поверхностном слое кристалла. Размеры кремниевых кристаллов лежат в пределах от примерно 1,3ґ1,3 мм до 13ґ13 мм. Прогресс в области интегральных схем привел к разработке технологий больших и сверхбольших интегральных схем (БИС и СБИС). Эти технологии позволяют получать ИС, каждая из которых содержит многие тысячи схем: в одном чипе может насчитываться более 1 млн. компонентов.

См. также ПОЛУПРОВОДНИКОВЫЕ ЭЛЕКТРОННЫЕ ПРИБОРЫ. Интегральные схемы обладают целым рядом преимуществ перед своими предшественниками - схемами, которые собирались из отдельных компонентов, монтируемых на шасси. ИС имеют меньшие размеры, более высокие быстродействие и надежность; они, кроме того, дешевле и в меньшей степени подвержены отказам, вызываемым воздействиями вибраций, влаги и старения. Миниатюризация электронных схем оказалась возможной благодаря особым свойствам полупроводников. Полупроводник - это материал, обладающий гораздо большей электропроводностью (проводимостью), чем такой диэлектрик, как стекло, но существенно меньшей, чем проводники, например, медь. В кристаллической решетке такого полупроводникового материала, как кремний, при комнатной температуре имеется слишком мало свободных электронов, чтобы обеспечить значительную проводимость. Поэтому чистые полупроводники обладают низкой проводимостью. Однако введение в кремний соответствующей примеси увеличивает его электрическую проводимость.

См. также ТРАНЗИСТОР. Легирующие примеси вводят в кремний двумя методами. Для сильного легирования или в тех случаях, когда точное регулирование количества вводимой примеси необязательно, обычно пользуются методом диффузии. Диффузию фосфора или бора выполняют, как правило, в атмосфере легирующей примеси при температурах между 1000 и 1150° С в течение от получаса до нескольких часов. При ионной имплантации кремний бомбардируют высокоскоростными ионами легирующей примеси. Количество имплантируемой примеси можно регулировать с точностью до нескольких процентов; точность в ряде случаев важна, поскольку коэффициент усиления транзистора зависит от числа примесных атомов, имплантированных на 1 см2 базы (см. ниже).

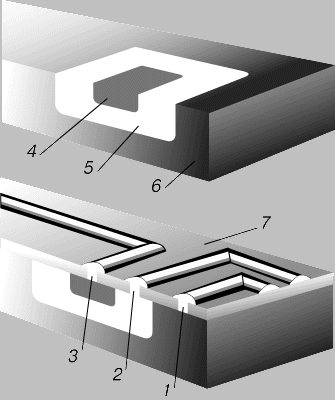
ВВЕДЕНИЕ ПРИМЕСЕЙ В КРЕМНИЙ методом диффузии - основа производства ИС. Для получения области коллектора с проводимостью n-типа добавляют фосфор, затем для создания области базы с проводимостью p-типа - бор и, наконец, снова фосфор для создания области эмиттера с проводимостью n-типа. 1 - контакт коллектора; 2 - контакт базы; 3 - контакт эмиттера; 4 - эмиттер (-); 5 - база (+); 6 - коллектор (-); 7 - защитный слой двуокиси кремния.

Производство. Изготовление интегральной схемы может занимать до двух месяцев, поскольку некоторые области полупроводника нужно легировать с высокой точностью. В ходе процесса, называемого выращиванием, или вытягиванием, кристалла, сначала получают цилиндрическую заготовку кремния высокой чистоты. Из этого цилиндра нарезают пластины толщиной, например, 0,5 мм. Пластину в конечном счете режут на сотни маленьких кусочков, называемых чипами, каждый из которых в результате проведения описываемого ниже технологического процесса превращается в интегральную схему. Процесс обработки чипов начинается с изготовления масок каждого слоя ИС. Выполняется крупномасштабный трафарет, имеющий форму квадрата площадью ок. 0,1 м2. На комплекте таких масок содержатся все составляющие части ИС: уровни диффузии, уровни межсоединений и т.п. Вся полученная структура фотографически уменьшается до размера кристаллика и воспроизводится послойно на стеклянной пластине. На поверхности кремниевой пластины выращивается тонкий слой двуокиси кремния. Каждая пластина покрывается светочувствительным материалом (фоторезистом) и экспонируется светом, пропускаемым через маски. Неэкспонированные участки светочувствительного покрытия удаляют растворителем, а с помощью другого химического реагента, растворяющего двуокись кремния, последний вытравливается с тех участков, где он теперь не защищен светочувствительным покрытием. Варианты этого базового технологического процесса используются в изготовлении двух основных типов транзисторных структур: биполярных и полевых (МОП).

Биполярный транзистор. Такой транзистор имеет структуру типа n-p-n или, намного реже, типа p-n-p. Обычно технологический процесс начинается с пластины (подложки) сильно легированного материала p-типа. На поверхности этой пластины эпитаксиально выращивается тонкий слой слабо легированного кремния n-типа; таким образом, выращенный слой имеет ту же самую кристаллическую структуру, что и подложка. Этот слой должен содержать активную часть транзистора - в нем будут сформированы индивидуальные коллекторы. Пластина сначала помещается в печь с парами бора. Диффузия бора в кремниевую пластину происходит только там, где ее поверхность подверглась обработке травлением. В результате формируются области и окна из материала n-типа. Второй высокотемпературный процесс, в котором используются пары фосфора и другая маска, служит для формирования контакта с коллекторным слоем. Проведением последовательных диффузий бора и фосфора формируются соответственно база и эмиттер. Толщина базы обычно составляет несколько микрон. Эти крошечные островки проводимостей n- и p-типа соединяются в общую схему посредством межсоединений, выполненных из алюминия, осаждаемого из паровой фазы или наносимого напылением в вакууме. Иногда для этих целей используются такие благородные металлы, как платина и золото. Транзисторы и другие схемные элементы, например резисторы, конденсаторы и индуктивности, вместе с соответствующими межсоединениями могут формироваться в пластине методами диффузии в ходе последовательности операций, создавая в итоге законченную электронную схему. См. также ТРАНЗИСТОР.

МОП-транзистор. Наибольшее распространение получила МОП (металл-окисел-полупроводник) - структура, состоящая из двух близко расположенных областей кремния n-типа, реализованных на подложке p-типа. На поверхности кремния наращивается слой его двуокиси, а поверх этого слоя (между областями n-типа и слегка захватывая их) формируется локализованный слой металла, выполняющий роль затвора. Две упомянутые выше области n-типа, называемые истоком и стоком, служат соединительными элементами для входа и выхода соответственно. Через окна, предусмотренные в двуокиси кремния, выполняются металлические соединения с истоком и стоком. Узкий поверхностный канал из материала n-типа соединяет исток и сток; в других случаях канал может быть индуцированным - создаваемым под действием напряжения, приложенного к затвору. Когда на затвор транзистора с индуцированным каналом подается положительное напряжение, расположенный под затвором слой p-типа превращается в слой n-типа, и ток, управляемый и модулируемый сигналом, поступающим на затвор, течет от истока к стоку. МОП-транзистор потребляет очень небольшую мощность; он имеет высокое входное сопротивление, отличается низким током цепи стока и очень низким уровнем шумов. Поскольку затвор, оксид и кремний образуют конденсатор, такое устройство широко используется в системах компьютерной памяти (см. ниже). В комплементарных, или КМОП-схемах, МОП-структуры применяются в качестве нагрузок и не потребляют мощности, когда основной МОП-транзистор находится в неактивном состоянии.

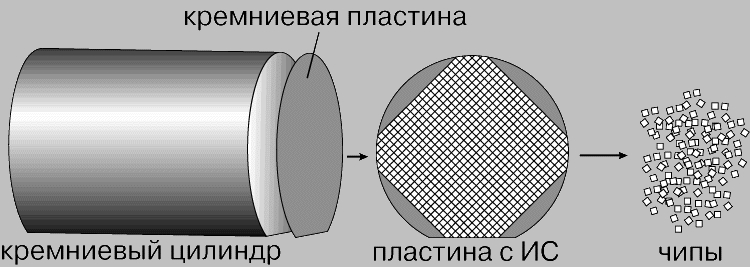
ИНТЕГРАЛЬНЫЕ СХЕМЫ. Очень чистый кристаллический кремний, необходимый для изготовления интегральных схем, выращивается в форме цилиндра, из которого затем нарезаются пластины, имеющие толщину бумажного листа. На каждой пластине создаются сотни ИС. Затем пластина разделяется на отдельные ИС, каждая из которых представляет собой квадратный кристалл (чип) со стороной 1,27 мм. ИС выпускаются в корпусах различных конфигураций.

После завершения обработки пластины разрезают на части. Операция резки выполняется дисковой пилой с алмазными кромками. Каждый кристаллик (чип, или ИС) заключается затем в корпус одного из нескольких типов. Для подсоединения компонентов ИС к рамке выводов корпуса используется золотая проволока толщиной 25 мкм. Более толстые выводы рамки позволяют подсоединить ИС к электронному устройству, в котором она будет работать.

Надежность. Надежность интегральной схемы примерно такая же, как у отдельного кремниевого транзистора, эквивалентного по форме и размеру. Теоретически транзисторы могут безотказно служить тысячи лет - один из важнейших факторов для таких областей применения, как ракетная и космическая техника, где единственный отказ может означать полный провал осуществляемого проекта.

Микропроцессоры и миникомпьютеры. Впервые представленные публично в 1971 микропроцессоры выполняли большинство основных функций компьютера на единственной кремниевой ИС, реализованной на кристалле размером 5ґ5 мм. Благодаря интегральным схемам стало возможным создание миникомпьютеров - малых ЭВМ, где все функции выполняются на одной или нескольких больших интегральных схемах. Такая впечатляющая миниатюризация привела к резкому снижению стоимости вычислений. Выпускаемые в настоящее время мини-ЭВМ ценой менее 1000 долл. по своей производительности не уступают первым очень большим вычислительным машинам, стоимость которых в начале 1960-х годов доходила до 20 млн. долл. Микропроцессоры находят применение в оборудовании для связи, карманных калькуляторах, наручных часах, селекторах телевизионных каналов, электронных играх, автоматизированном кухонном и банковском оборудовании, средствах автоматического регулирования подачи топлива и нейтрализации отработавших газов в легковых автомобилях, а также во многих других устройствах. Большая часть мировой электронной индустрии, оборот которой превышает 15 млрд. долл., так или иначе зависит от интегральных схем. В масштабах всего мира интегральные схемы находят применение в оборудовании, суммарная стоимость которого составляет многие десятки миллиардов долларов.

Компьютерные запоминающие устройства. В электронике термин "память" обычно относится к какому-либо устройству, предназначенному для хранения информации в цифровой форме. Среди множества типов запоминающих устройств (ЗУ) рассмотрим ЗУ с произвольной выборкой (ЗУПВ), приборы с зарядовой связью (ПЗС) и постоянные ЗУ (ПЗУ). У ЗУПВ время доступа к любой ячейке памяти, находящейся на кристалле, одинаково. Такие устройства могут запоминать 65 536 бит (двоичных единиц, обычно 0 и 1), по одному биту на ячейку, и представляют собой широко используемый тип электронной памяти; на каждом чипе у них насчитывается ок. 150 тыс. компонентов. Выпускаются ЗУПВ емкостью 256 Кбит (К = 210 = 1024; 256 К = 262 144). В устройствах памяти с последовательной выборкой циркуляция запомненных битов происходит как бы по замкнутому конвейеру (в ПЗС используется именно такой тип выборки). В ПЗС, представляющем собой ИС специальной конфигурации, пакеты электрических зарядов могут размещаться под расположенными на малых расстояниях друг от друга крошечными металлическими пластинками, электрически изолированными от чипа. Заряд (или его отсутствие) может, таким образом, перемещаться по полупроводниковому устройству от одной ячейки к другой. В результате появляется возможность запоминания информации в виде последовательности единиц и нулей (двоичного кода), а также доступа к ней, когда это требуется. Хотя ПЗС не могут конкурировать с ЗУПВ по быстродействию, они способны обрабатывать большие объемы информации при меньших затратах, и их используют там, где память с произвольной выборкой не требуется. ЗУПВ, выполненное на такой ИС, является энергозависимым, и записанная в нем информация теряется при отключении питания. В ПЗУ информация заносится в ходе производственного процесса и хранится постоянно. Разработки и выпуск ИС новых типов не прекращаются. В стираемых программируемых ПЗУ (СППЗУ) имеются два затвора, расположенные один над другим. При подаче напряжения на верхний затвор нижний может приобрести заряд, что соответствует 1 двоичного кода, а при переключении (реверсе) напряжения затвор может потерять свой заряд, что соответствует 0 двоичного кода.

См. также

ОРГТЕХНИКА И КАНЦЕЛЯРСКОЕ ОБОРУДОВАНИЕ;

КОМПЬЮТЕР;

ЭЛЕКТРОННЫЕ СРЕДСТВА СВЯЗИ;

ИНФОРМАЦИИ НАКОПЛЕНИЕ И ПОИСК.

ЛИТЕРАТУРА

Мейзда Ф. Интегральные схемы: технология и применения. М., 1981 Зи С. Физика полупроводниковых приборов. М., 1984 Технология СБИС. М., 1986 Маллер Р., Кеймин С. Элементы интегральных схем. М., 1989 Шур М.С. Физика полупроводниковых приборов. М., 1992

Составить слова из слова интегральная схема

нареч, кол-во синонимов: 3

совокупно, едино, цельно

Составить слова из слова интегрально

интегра/льно-пропорциона/льный

Составить слова из слова интегрально-пропорциональный

Интегра́льное исчисле́ние - раздел математики, в котором изучаются свойства и способы вычисления интегралов и их приложения к решению различных математических, физических и других задач. В систематической форме интегральное исчисление было предложено в XVII в. И. Ньютоном и Г. Лейбницем. Интегральное исчисление тесно связано с дифференциальным исчислением; интегрирование (нахождение интеграла) есть действие, обратное дифференцированию: по данной непрерывной функции f(x) ищется функция F(x) (первообразная), для которой f(x) является производной. Вместе с(х) первообразной функцией для f(x) является и f(x) + С, где С - любая постоянная. Общее выражение F(х) + С первообразных непрерывной функции f(x) называется неопределённым интегралом; он обозначается

∫f(x)dx = F(х) + С.

Определённым интегралом непрерывной функции f(х) на отрезке [а, b], разделённом точками x₁, х₂,..., x_n-1, называется предел интегральных сумм 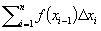, где Δх_i = x_i - x_i-1, при условии, что наибольшая разность Δx_i стремится к нулю и число точек деления неограниченно увеличивается; его обозначают ">Кратный интеграл, Криволинейный интеграл, Поверхностный интеграл).

">

* * *

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ - ИНТЕГРА́ЛЬНОЕ ИСЧИСЛЕ́НИЕ, раздел математики, в котором изучаются свойства и способы вычисления интегралов и их приложения к решению различных математических, физических и других задач. В систематической форме интегральное исчисление было предложено в 17 в. И. Ньютоном и Г. Лейбницем. Интегральное исчисление тесно связано с дифференциальным исчислением (см. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ); интегрирование (нахождение интеграла) есть действие, обратное дифференцированию: по данной непрерывной функции f(x) ищется функция F(x) (первообразная), для которой f(x) является производной. Вместе с F(x) первообразной функцией для f(x) является и F(x) + C, где С - любая постоянная. Общее выражение F(x) + C первообразных непрерывной функции f(x) называется неопределенным интегралом; он обозначается

Определенным интегралом непрерывной функции f(x) на отрезке [a, b], разделенном точками (рис.), называется предел интегральных сумм , где , при условии, что наибольшая разность стремится к нулю и число точек деления неограниченно увеличивается; его обозначают (самый знак возник из первой буквы S латинского слова Summa). Через определенные интегралы выражаются площади плоских фигур, длины кривых, объемы и поверхности тел, координаты центров тяжести, моменты инерции, работа, производимая данной силой, и т. д. О связи между определенным интегралом и первообразной см. -Ньютона Лейбница формула (см. НЬЮТОНА-ЛЕЙБНИЦА ФОРМУЛА). Понятие интеграла распространяется на функции многих переменных (см. Кратный интеграл (см. КРАТНЫЙ ИНТЕГРАЛ), Криволинейный интеграл (см. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ), Поверхностный интеграл (см. ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ))

ИНТЕГРАЛЬНОЕ исчисление - раздел математики, в котором изучаются свойства и способы вычисления интегралов и их приложения к решению различных математических, физических и других задач. В систематической форме интегральное исчисление было предложено в 17 в. И. Ньютоном и Г. Лейбницем. Интегральное исчисление тесно связано с дифференциальным исчислением; интегрирование (нахождение интеграла) есть действие, обратное дифференцированию: по данной непрерывной функции f(x) ищется функция F(x) (первообразная), для которой f(x) является производной. Вместе с F(x) первообразной функцией для f(x) является и F(x) + C, где С - любая постоянная. Общее выражение F(x) + C первообразных непрерывной функции f(x) называется неопределенным интегралом; он обозначается.Определенным интегралом непрерывной функции f(x) на отрезке ИНТЕГРАЛЬНОЕ уравнение - уравнение, содержащее неизвестную функцию под знаком интеграла.

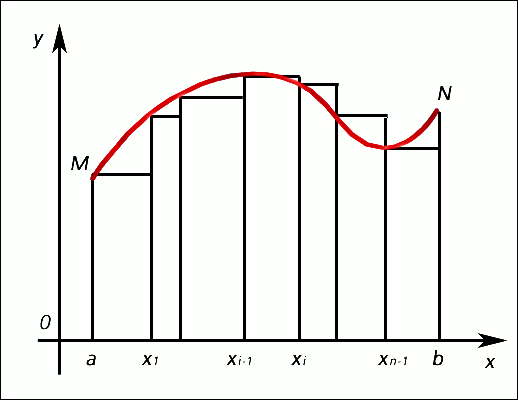
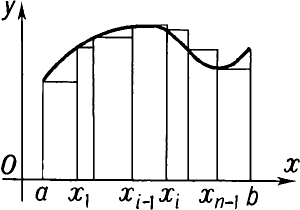
Интегральное исчисление. Построение интегральных сумм для вычисления определенного интеграла непрерывной функции f(x), график которой - кривая MN.

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ, раздел математики, в котором изучаются свойства и способы вычисления интегралов и их приложения к решению различных математических и физических задач. В систематической форме интегральное исчисление было предложено в 17 в. И. Ньютоном и Г. Лейбницем. Интегральное исчисление тесно связано с дифференциальным исчислением; интегрирование (нахождение интеграла) есть действие, обратное дифференцированию: по данной непрерывной функции f(x) ищется функция F(x) (первообразная), для которой f(x) является производной. Вместе с F(x) первообразной функцией для f(x) является и F(x)+C,

где C - любая постоянная. Общее выражение F(x)+C первообразных непрерывной функции f(x)

называется неопределенным интегралом; он обозначается

.

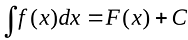Определенным интегралом непрерывной функции f(x) на отрезке [a,b], разделенном точками

x₁, x₂, ..., x_n-1, называется предел интегральных сумм

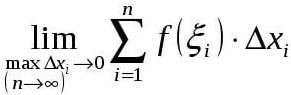
 где Dx_i-x_i-1,

при условии, что наибольшая разность стремится к нулю и число

точек деления неограниченно увеличивается; его обозначают

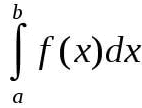
(самый знак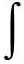

 возник из первой буквы S латинского слова Summa). Через определенные интегралы выражаются площади плоских фигур, длины кривых, объемы и поверхности тел, координаты центров тяжести, моменты инерции, работа, производимая данной силой, и т.д.

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ - отдел высшей математики, учение о действиях, противоположных дифференциальному вычислению, а именно - об определении зависимости между несколькими переменными величинами по данному дифференциальному уравнению из них. Таким образом, находится количество, определяемое малейшей ею частью.

Составить слова из слова интегральное исчисление

Часть высшего анализа, излагающая правила, как по данному количеству находить величину, дифференциал которой равняется этому количеству.

Составить слова из слова интегральное счисление

Интегра́льное уравне́ние - уравнение, содержащее неизвестную функцию под знаком интеграла.

* * *

ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ - ИНТЕГРА́ЛЬНОЕ УРАВНЕ́НИЕ, уравнение, содержащее неизвестную функцию под знаком интеграла.

Составить слова из слова интегральное уравнение

интегральные семы синонимической парадигмы - вычленяются из лексического значения доминанты.

интегральные семы синонимической парадигмы - вычленяются из лексического значения доминанты.

Составить слова из слова интегральные семы синонимической парадигмы

ИНТЕГРАЛЬНЫЕ ФУНКЦИИ - ИНТЕГРА́ЛЬНЫЕ ФУ́НКЦИИ, родственные между собой специальные функции второго рода, определяемые с помощью интегралов от элементарных функций. Примеры: интегральные синус, косинус, логарифм, показательная функция; интегралы вероятности и Френеля. Введены Л. Эйлером (см. ЭЙЛЕР Леонард) в 1768.

Составить слова из слова интегральные функции

I прил.

1. соотн. с сущ. интеграл, связанный с ним

2. Свойственный интегралу, характерный для него.

II прил.

Неразрывно связанный; цельный, единый.

ИНТЕГРА́ЛЬНЫЙ, интегральная, интегральное.

1. прил. к интеграл (мат.). Интегральное исчисление. Интегральная функция.

2. Неразрывно-связанный, составляющий неотъемлемую часть целого (научн.).

ИНТЕГРА́Л [тэ], -а, м. В математике: величина, получающаяся в результате действия, обратного дифференцированию.

-ая, -ое; -лен, -льна, -льно.

1. только полн. ф. мат.

прил. к интеграл.

Интегральное исчисление (раздел математики, в котором изучаются свойства и способы вычисления интегралов и их приложения).

Интегральные уравнения (содержащие неизвестные функции под знаком интеграла).

2. книжн.

Цельный, единый.

Если определенный тип организма не интегрален, но распадается на два или более соподчиненных по своим свойствам, то, кроме основного обозначения, соответствующего существительному, прибавляется еще прилагательное, более точно обозначающее свойства данного организма. В. Комаров, Учение о виде у растений.

интегра́льный

интегра́льный, интегра́льная, интегра́льное, интегра́льные, интегра́льного, интегра́льной, интегра́льных, интегра́льному, интегра́льным, интегра́льную, интегра́льною, интегра́льными, интегра́льном, интегра́лен, интегра́льна, интегра́льно, интегра́льны, интегра́льнее, поинтегра́льнее, интегра́льней, поинтегра́льней

прил., кол-во синонимов: 4

накопленный, кумулятивный; совокупный, цельный, единый. Ant. рассеяние, разъединение

Syn: накопленный, кумулятивный

Ant: рассеяние, разъединение

разрозненный

дифференциальный

интегр/а́ль/н/ый.

интегра́льный п 1*a

ИНТЕГРАЛЬНЫЙ ая, ое. intégral, нем.integral <, лат. integralis.

1. Отн. к интегралу. Сл. 18. О щете интегралном. Прим. Вед. 1728 40. Действия сея силы сыскивают посредством интегральнаго счисления. Астр. Лаланда 574. // Сл. 18. Дифференциальное, интегральное и вариационное исчисление. 1797. Алгебра Барсов (т. л.). ♦ Интегральное исчисление. Интегральная функция. Уш. 1934.

2. научн. Неразрывно-связанный, составляющий неотъемлемую часть целого. Уш. 1934. Хотя мы не можем представить себе, что делимость тел имела пределы; но если тела состоят из атомов или самомалейших интегральных частиц, то делимость не может простираться до бесконечности. Спасский Горн. сл. 1841. Между тем в этом определении и дальнейшем его развитии, что в опере три интегральных элемента: поэтический текст ( le poème), музыка и декорация, - Руссо весьма близок к истине. 1859. А. Серов Ст. о муз. 4 16. Государство мыслило себя "православным государством" и церковь - своей интегральной частью. Континент 2002 2 342. ♦ Интегральная кооперация. Кооперативная система смешанного типа, объединяющая все виды деятельности кооперации: потребительскую, промысловую, сельскохозяйственную, охотничью и др.; существовала до 1936 г. на советском Крайнем Севере. СИС 1954.

3. полит. Цельный, полный. Буржуазные партии берут у интегральных националистов их два основных принципа: национальный интерес и национальное единение. РБ 1913 9 302. Интегральный националист. Соврем. 1913 12 162. И только социал-демократы большевики с самого начала войны и до конца оставались интегральными пораженцами, пойдя на оплачиваемое сотрудничество со штабами воевавших с нами центральных держав. Деникин Путь рус. офицера. // Октябрь 1991 3 115. - Лекс. Ян. 1803: интегральный; САН 1847: интегра/льный; Сл. 18: интеграл(ь)ный 1728.

ИНТЕГРАЛЬНЫЙ (н.-лат.). Неразрывно-связанный.

Составить слова из слова интегральный

Интегральный билингвизм (Адекватный билингвизм)

Вид билингвизма, при котором оба языка (родной и второй) в одинаковой степени выполняют весь объем функций, независимо от ситуации и сферы общения.

(Адекватный билингвизм)

Вид билингвизма, при котором оба языка (родной и второй языки) в полной и одинаковой мере способны выполнять весь объем функций, независимо от ситуации и темы общения. Однако это достаточно редкое явление.

♦ билингвизм

См. также: Билингвизм, Регрессивный билингвизм

Составить слова из слова интегральный билингвизм

Вид билингвизма, при котором оба языка (родной и второй) в одинаковой степени выполняют весь объем функций, независимо от ситуации и сферы общения.

Составить слова из слова интегральный билингвизм (адекватный билингвизм)

ИНТЕГРА́ЛЬНЫЙ (от лат. integer - целый) МЕ́ТОД ОБУЧЕ́НИЯ.

Один из вариантов комбинированного метода обучения. Включает признаки, присущие сознательно-практическому, аудиовизуальному методам обучения, а также элементы программирования и суггестии, что позволяет относить этот метод обучения к группе комбинированных методов.

Опирается на следующие методические принципы, определяемые создателями метода (Г. Крампиц):

1. Преподавание языка имеет коммуникативную и страноведческую направленность. Коммуникативная направленность метода диктует отбор учебного материала, отражающего необходимые для учащихся сферы общения, и использование коммуникативных упражнений. Страноведческая направленность метода предполагает включение тем и ситуаций, знакомящих с различными сторонами жизни страны изучаемого языка.

2. Обучение ориентировано на формирование речевых навыков и развитие речевых умений. Организуется комплексное параллельное овладение всеми видами речевой деятельности с преобладанием слушания и говорения, а также с учетом различий между устной и письменной речью.

3. В качестве единицы обучения рассматривается предложение, а введение и закрепление материала осуществляется путем обучения на синтаксической основе.

4. Занятия организуются в последовательности от выработки автоматизма речевых действий, формируемых сознательно, к речевым умениям. Сознательное усвоение материала при этом сочетается с интуитивным его осмыслением на основе звучащего или читаемого текста и др.

5. Интерференция родного языка вытесняется, ибо родной язык применяется только тогда, когда это методически необходимо. Считается, что с помощью этого метода удается значительно интенсифицировать обучение русскому языку при профессиональной направленности занятий.

Составить слова из слова интегральный метод обучения

ИНТЕГРАЛЬНЫЙ ОПЕРАТОР - ИНТЕГРА́ЛЬНЫЙ ОПЕРА́ТОР, обобщение понятия матрицы (см. МАТРИЦА (в математике)) на бесконечномерный случай. Возникает при использовании интегральных преобразований.

Составить слова из слова интегральный оператор

Общий признак, который не может быть использован для разграничения фонем языка. Например, русские гласные [э] и [о] - неносовые, следовательно, это интегральный признак.

Составить слова из слова интегральный признак при характеристике фонем