Дека́ртов, -а, -о (Дека́ртова филосо́фия); но: дека́ртова систе́ма координа́т, дека́ртов ли́ст, дека́ртов ова́л
декартов лист
Энциклопедический словарь
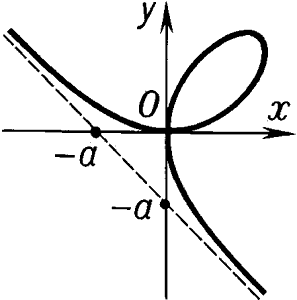
Дека́ртов лист - алгебраическая кривая 3-го порядка: х3 + у3 - 3аху = 0. Рассмотрена Р. Декартом (1638).
* * *
ДЕКАРТОВ ЛИСТ - ДЕКА́РТОВ ЛИСТ, алгебраическая кривая третьего порядка: х3 + у3 - 3аху = 0. Рассмотрена Р. Декартом (1638).
Большой энциклопедический словарь
ДЕКАРТОВ ЛИСТ - алгебраическая кривая 3-го порядка: х3 + у3 - 3аху = 0. Рассмотрена Р. Декартом (1638).
Полезные сервисы
декартова система координат
Энциклопедический словарь
ДЕКАРТОВА СИСТЕМА КООРДИНАТ - ДЕКА́РТОВА СИСТЕ́МА КООРДИНА́Т, прямолинейная система координат на плоскости или в пространстве (обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям). Названа по имени Р. Декарта (см. ДЕКАРТ Рене).
Декарт впервые ввел координатную систему, которая существенно отличалась от общепринятой в наши дни. Он использовал косоугольную систему координат на плоскости, рассматривая кривую относительно некоторой прямой с фиксированной системой отсчета. Положение точек кривой задавалось с помощью системы параллельных отрезков, наклонных или перпендикулярных к исходной прямой. Декарт не вводил второй координатной оси, не фиксировал направления отсчета от начала координат. Только в 18 в. сформировалось современное понимание координатной системы, получившее имя Декарта.
***
Для задания декартовой прямоугольной системы координат выбирают взаимно перпендикулярные прямые, называемые осями. Точка пересечения осей O называется началом координат. На каждой оси задается положительное направление и выбирается единица масштаба. Координаты точки P считаются положительными или отрицательными в зависимости от того, на какую полуось попадает проекция точки P.
Двухмерная система координат
Декартовыми прямоугольными координатами точки P на плоскости в двухмерной системе координат называются взятые с определенным знаком расстояния (выраженные в единицах масштаба) этой точки до двух взаимно перпендикулярных прямых - осей координат или проекции радиус-вектора r точки P на две взаимно перпендикулярные координатные оси.
В двухмерной системе координат горизонтальная ось называется осью абсцисс (ось OX), вертикальная ось - осью ординат (ось ОY). Положительные направления выбирают на оси OX - вправо, на оси OY - вверх. Координаты x и y называются соответственно абсциссой и ординатой точки. Запись P(a,b) означает, что точка P на плоскости имеет абсциссу a и ординату b.
Трехмерная система координат
Декартовыми прямоугольными координатами точки P в трехмерном пространстве называются взятые с определенным знаком расстояния (выраженные в единицах масштаба) этой точки до трех взаимно перпендикулярных координатных плоскостей или проекции радиус-вектора (см. РАДИУС-ВЕКТОР) r точки P на три взаимно перпендикулярные координатные оси.
Через произвольную точку пространства O - начало координат - проведены три попарно перпендикулярные прямые: ось OX (ось абсцисс), ось OY (ось ординат), ось OZ (ось аппликат).
На осях координат могут задаваться единичные вектора i, j, k по осям OX,OY, OZ соответственно.
В зависимости от взаимного расположения положительных направлений координатных осей возможны правая и левая координатные системы. Как правило, пользуются правой системой координат. В правой системе координат положительные направления выбирают следующим образом: по оси OX - на наблюдателя; по оси OY - вправо; по оси OZ - вверх. В правой системе координат кратчайший поворот от оси X к оси Y осуществляется против часовой стрелки; если одновременно с таким поворотом двигаться вдоль положительного направления оси Z, то получится движение по правилу правого винта.
Запись P(a,b,c) означает, что точка Р имеет абсциссу a, ординату b и аппликату c.
Каждая тройка чисел (a,b,c) задает единственную точку Р. Следовательно, прямоугольная декартова система координат устанавливает взаимно однозначное соответствие между множеством точек пространства и множеством упорядоченных троек действительных чисел.
Кроме координатных осей существуют также координатные плоскости. Координатными поверхностями, для которых одна из координат остается постоянной, здесь являются плоскости, параллельные координатным плоскостям, а координатными линиями, вдоль которых меняется только одна координата, - прямые, параллельные координатным осям. Координатные поверхности пересекаются по координатным линиям.
Координатная плоскость XOY содержит оси OX и OY, координатная плоскость YOZ содержит оси OY и OZ, координатная плоскость XOZ содержит оси OX и OZ.
Полезные сервисы
декартовы координаты
Энциклопедический словарь
Дека́ртовы координа́ты (декартова система координат), система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям - прямоугольные декартовы координаты. Названы по имени Р. Декарта.
Большой энциклопедический словарь
ДЕКАРТОВЫ координаты (декартова система координат) - система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям - прямоугольные декартовы координаты. Названы по имени Р. Декарта.