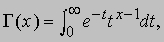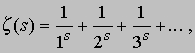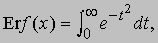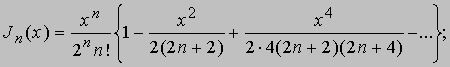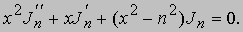I ж.

Зависимая переменная величина (в математике).

II ж.

Проявление жизнедеятельности организма, органа, тканей, клеток и т.п. (в физиологии).

III ж.

Явление, зависящее от другого, основного явления и служащее формой его проявления или осуществления.

IV ж.

1. Значение, назначение, роль.

2. Обязанность, круг деятельности, подлежащая исполнению работа.

ФУ́НКЦИЯ - сущ., ж., употр. сравн. часто

Морфология: (нет) чего? фу́нкции, чему? фу́нкции, (вижу) что? фу́нкцию, чем? фу́нкцией, о чём? о фу́нкции; мн. что? фу́нкции, (нет) чего? фу́нкций, чему? фу́нкциям, (вижу) что? фу́нкции, чем? фу́нкциями, о чём? о фу́нкциях

1. Функцией называется назначение, роль какого-либо объекта.

Дополнительные функции и возможности в мобильных телефонах.

2. Функцией называется значение элемента какой-либо структуры, системы языка.

Звательный падеж в функции именительного.

3. Функцией называется конкретное направление деятельности человека или профессиональной группы людей.

Взять на себя функцию распорядителя. | Выполнять чью-либо функцию. | Возложить на комитет функции контроля.

4. В медицине функцией какого-либо органа человеческого тела называется внешнее проявление его свойств, работа, которая им производится в связи с другими органами.

Восстановление нарушенных функций организма. | Пищеварительная, выделительная функция.

5. В математике функцией называется зависимость одних числовых величин от других.

Тригонометрические функции.

6. В компьютерном программировании функцией называется устойчивая операция по управлению каким-либо логическим процессом.

Вызвать, использовать, определить, объявить функцию. | Графические функции. | Функция ввода.

ФУ́НКЦИЯ, функции, жен. (лат. functio - выполнение работы).

1. Явление, зависящее от другого и изменяющееся по мере изменения этого другого явления (книжн.).

2. Переменная величина, меняющаяся в зависимости от изменения другой величины (мат.). Величина давления газа есть функция величины его объема.

3. Работа, производимая органом, организмом (биол., физиол.). Отделение слюны является основной функцией слюнной железы.

4. перен. Обязанность, круг деятельности чего-нибудь, подлежащая исполнению работа (книжн.). Служебные функции. Исполнять свою функцию в обществе. Функции государственного управления.

5. Значение, назначение, роль (книжн.). Функция математического знака. Функция родительного падежа.

ФУ́НКЦИЯ, -и, жен.

1. В философии: явление, зависящее от другого и изменяющееся по мере изменения этого другого явления.

2. В математике: закон, по к-рому каждому значению переменной величины (аргумента) ставится в соответствие нек-рая определённая величина, а также сама эта величина. Линейная ф. (меняющаяся прямо пропорционально изменению своего аргумента).

3. Работа производимая органом, организмом (книжн.). Ф. желёз.

4. Роль, значение чего-н. (книжн.). Функции кредита.

5. Обязанность, круг деятельности (книжн.). Служебные функции. Функции профкома.

| прил. функциональный, -ая, -ое (к 1, 2, 3 и 4 знач.).

ФУНКЦИЯ - жен., мат. обозначенье действий над количествами.

| Физиол. отправленье членами тела своих действий.

ФУ́НКЦИЯ^1́, -и, ж Спец.

Физиологический процесс, связанный с работой какого-л. органа в живом организме и свидетельствующий о его жизнедеятельности.

Каждый третий из комиссованных проходил по заболеваниям нервно-психической сферы и внутренних органов… каждый второй с нарушениями, как пишут в медицинских документах, опорно-двигательных функций, то есть не мог нормально ходить и владеть руками (Газ.).

ФУ́НКЦИЯ^2́, -и, ж

Круг занятий, направление деятельности в соответствии с назначением какой-л. организации, учреждения; задача, обязанность должностного лица.

Возложить на комитет функции контроля.

функция

1. Роль, выполняемая языковой единицей при воспроизведении в речи.

2. Назначение, применение, использование разных сторон языка и его элементов.

ФУ́НКЦИЯ -и; ж. [от лат. functio]

1. Значение, назначение чего-л. Ф. кредита. Звательный падеж в функции именительного. Выполнять чью-л. функцию. Нести, взять на себя функцию администратора, распорядителя. // Направление деятельности в соответствии с назначением какой-л. организации, учреждения; задача, обязанность должностного лица и т.п. Ф. кооперации. Возложить на комитет функции контроля.

2. Биол. Работа, производимая органом или организмом, как проявление его жизнедеятельности. Ф. надпочечников. Восстановление нарушенных функций организма. Пищеварительная, выделительная ф. Физиологические функции. Отправлять свои функции (о действии отдельных органов).

3. Матем. Зависимость одних переменных величин от других; переменная величина, меняющаяся в зависимости от изменения другой величины (аргумента). Тригонометрические функции.

4. Книжн. Явление, зависящее от другого и служащее формой его проявления, осуществления. Литература признаётся одной из функций общественного бытия.

◁ Функциона́льный (см.).

* * *

функция - I

(от лат. functio - исполнение, осуществление), 1) деятельность, обязанность, работа; внешнее проявление свойств какого-либо объекта в данной системе отношений (например, функция органов чувств, функция денег). 2) Функция в социологии - роль, которую выполняет определенный социальный институт или процесс по отношению к целому (например, функция государства, семьи и т. д. в обществе). 3) (Лингв.) назначение, роль (иногда и значение) языковой единицы или элемента языковой структуры.

II

(матем.), 1) зависимая переменная величина.

2) Соответствие у = f(х) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины х (аргумента, или независимого переменного) соответствует определённое значение другой величины y (зависимой переменной, или функции). Такое соответствие может быть задано различным образом, например формулой, графически или таблицей (типа таблицы логарифмов). С помощью функций математически выражаются многообразные количественные закономерности в природе.

ФУНКЦИЯ - в математике - ..1) зависимая переменная величина

2)] Соответствие y = f (x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента, или независимого переменного) соответствует определенное значение другой величины y (зависимой переменной, или функции). Такое соответствие может быть задано различным образом, напр. формулой, графически или таблицей (типа таблицы логарифмов). С помощью функции математически выражаются многообразные количественные закономерности в природе.

-----------------------------------

ФУНКЦИЯ (от лат. functio - исполнение - осуществление),..1) деятельность, обязанность, работа; внешнее проявление свойств какого-либо объекта в данной системе отношений (напр., функция органов чувств, функция денег)

2)] Функция в социологии - роль, которую выполняет определенный социальный институт или процесс по отношению к целому (напр., функция государства, семьи и т. д. в обществе)

3) В лингвистике - назначение, роль (иногда и значение) языковой единицы или элемента языковой структуры.

-и, ж.

1. Явление, зависящее от другого и изменяющееся по мере изменения другого явления.

Литература в целом мире признается как одна из функций общественного бытия. Салтыков-Щедрин, Признаки времени.

2. мат.

Переменная величина, меняющаяся в зависимости от изменения другой величины (аргумента).

Тригонометрические функции.

◊

[Володя], бойко постукивая мелом о черную доску, толкует о функциях, синусах, координатах и т. п. Л. Толстой, Отрочество.

3. биол.

Работа, производимая органом, организмом, как проявление его жизнедеятельности.

Вот вам азбука биологии: если какой-нибудь орган продолжительное время не упражнять, то он утрачивает способность отправлять свои функции. Федин, Города и годы.

[Котельников:] Проблема сводится к восстановлению жизненных функций организма, пораженного тем или иным ядом. Лавренев, Мы будем жить!

4. перен.

Обязанность, круг деятельности.

- [Развалихин] утром сказал, что пойдет в школу проводить обществоведение вместо тебя. «Это, говорит, моя прямая функция, а не Корчагина». Н. Островский, Как закалялась сталь.

5. Значение, назначение, роль.

Функция творительного падежа. Функции денег.

[От лат. functio - исполнение]

ФУНКЦИЯ - термин, используемый в математике для обозначения такой зависимости между двумя величинами, при которой если одна величина задана, то другая может быть найдена. Обычно функция (с 17 в.) задается формулой, выражающей зависимую переменную через одну или несколько независимых переменных. Например, площадь круга есть функция его радиуса, и эта зависимость записывается формулой A = pr2; периметр прямоугольника является функцией его длины и ширины или P = 2(l + w). Функцию можно изобразить графически, нанося точки, координатами которых служат независимые и зависимые переменные, на координатную плоскость (рис. 1).

См. также АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ.

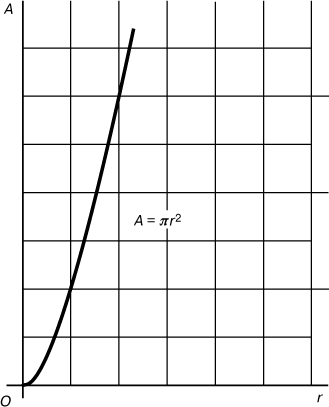
Рис. 1. ГРАФИК ФУНКЦИИ A = pr 2 (площадь круга как функция радиуса).

Считалось, что график, подобный изображенному на рис. 2, не может быть графиком одной функции, так как различные его части должны описываться различными формулами (y = x для x от 0 до 1; y = -x для x от -1 до 0; y = 2 - x для x от 1 до 2 и т.д.). Каково же было удивление математиков, когда в начале 19 в. они обнаружили, что график функции, изображенной на рис. 2, в действительности определяется формулой

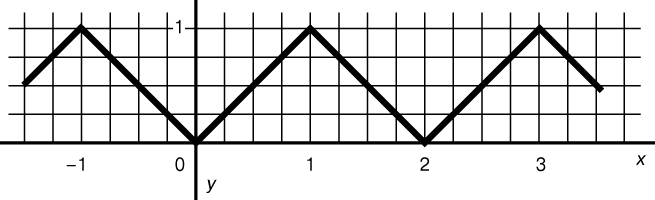
Рис. 2. ГРАФИК ФУНКЦИИ, представимой в виде бесконечного ряда.

где многоточие указывает на то, что формула неограниченно продолжается аналогичным образом.

См. также РЯДЫ. Это открытие привело к пересмотру определения функции. Согласно новому определению, под функцией надлежит понимать любое правило, позволяющее находить одно число (значение зависимой переменной), если задано другое число или набор чисел (значений независимых переменных). Такое правило может быть выражено формулой, но это необязательно. Его можно задать графически или просто описать словами. Например, "наибольшее целое число, не превосходящее x" обозначается как [[x]] и представляется графически, как показано на рис. 3. Другой пример: правило "продолжительность дня x заданного года в часах". При таком описательном определении функции отпадает необходимость предполагать, что независимая и зависимая переменные - числа; они могут быть чем угодно. Например, положение города на карте является функцией его положения на поверхности Земли, а фамилию взрослого человека можно определить как функцию номера его паспорта. В каждом случае первое может быть найдено, если задано второе. Наряду с термином "функция" употребляют также равнозначные ему термины "отображение", "операция", "преобразование", "соответствие". Например, функцию, заданную формулой y = x2, можно представить как отображение оси x на ось y, как операцию возведения числа x в квадрат и как преобразование, превращающее число x в его квадрат.

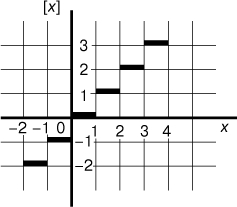
Рис. 3. ПЕРЕСМОТРЕННОЕ ОПРЕДЕЛЕНИЕ ФУНКЦИИ в графической форме.

В настоящее время такое определение функции заменено более общим. Определение функции как правила, ставящего в соответствие значение зависимой переменной каждому значению независимой переменной, не удовлетворяло, поскольку не определяло функцию как математический объект. Чтобы пояснить новое определение, предположим, что у нас имеется некоторое множество элементов A. Рассмотрим набор таких упорядоченных пар (a,b) (упорядоченность означает, что пара (a,b) считается отличной от пары (b,a)), в которых a принадлежит множеству A, а b может принадлежать A или какому-нибудь другому множеству. Такой набор упорядоченных пар называется отношением. Примерами могут служить пары чисел (x,x2) при любых значениях x; пары чисел (x,y), таких, что y < x2; или пары (a,b) отцов (a) и сыновей (b), в которых каждый отец встречается столько раз, сколько у него сыновей. Второй элемент упорядоченной пары не всегда определяется однозначно, если задан ее первый элемент. В первом примере он может быть однозначно определен, так как любое число имеет только один квадрат, но во втором и третьем примерах это не так, поскольку существует много чисел y, меньших, чем квадрат данного числа x, а у одного отца может быть несколько сыновей. Если второй элемент упорядоченной пары можно найти при заданном первом элементе, то каждый первый элемент встречается только один раз, и такое отношение называется функцией. Таким образом, функцией является только первое из трех приведенных выше примеров отношений. Если пары отцов и сыновей записать в обратном порядке, то они образуют функцию, так как у каждого сына есть только один отец. В более старой терминологии отношение, удовлетворяющее этому определению, называлось однозначной функцией, а некоторые другие типы отношений - многозначными функциями. Если функция задана графически, то упорядоченные пары представляют собой не что иное, как координаты точек графика, и новое определение сводится к утверждению, что функция есть геометрическое место точек, совпадающее с графиком. Традиционная запись y = f(x) означает, что y является функцией от x. Переменная x называется аргументом функции. Многие конкретные функции имеют свои названия; обычно такие функции задаются формулами. К числу элементарных функций относятся многочлены

логарифмическая функция, экспоненциальная функция, тригонометрические функции и их конечные комбинации. Примерами некоторых неэлементарных функций могут служить гамма-функция Эйлера

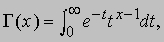
обобщающая факториал целого числа на нецелые значения x; при положительных целых x функция Г(x) сводится к (x - 1)! = 1*2*3*...*(x - 1) (это произведение называется факториалом числа x - 1); дзета-функция Римана

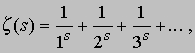
играющая важную роль в теории чисел, и функция ошибок

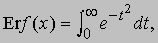
встречающаяся в статистике. В математической физике используются функции Бесселя

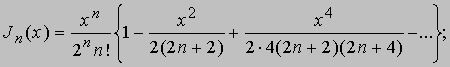
удовлетворяющие дифференциальному уравнению

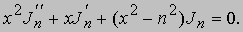
См также

АБСТРАКТНЫЕ ПРОСТРАНСТВА;

МАТЕМАТИЧЕСКИЙ АНАЛИЗ;

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ;

ФУНКЦИЙ ТЕОРИЯ;

ЛОГАРИФМ;

ЧИСЛО;

МНОЖЕСТВ ТЕОРИЯ.

ФУНКЦИЯ (от латинского functio - исполнение, осуществление),

1) деятельность, обязанность, работа; внешнее проявление свойств какого-либо объекта в данной системе отношений (например, функция органов чувств, функция денег).

2) Функция в социологии - роль, которую выполняет определенный социальный институт или процесс по отношению к целому (например, функция государства, семьи и т.д. в обществе).

3) Функция в математике - соответствие между переменными величинами, в силу которого каждому значению одной величины x (независимого переменного, аргумента) соответствует определенное значение другой величины y (зависимого переменного, функции). Функции могут быть заданы, например, формулой, графиком, таблицей, правилом.

ФУНКЦИЯ -

комплекс операций, посредством которых проявляет себя органическая, физическая и социальная жизнь. Когда Кант говорит, что ум - это функция, он имеет в виду, что ум существует не как абстрактная способность, но что, наоборот, он сводится к операциям познания и к действиям, посредством которых он себя проявляет (и «функционирует»).

функция (иноск.) - деятельность, обязанность (собств. должность)

Ср. В душе каждый из нас считал себя предназначенным для выполнения более высших функций, чем, например, копание помойных ям или чистка их.

М. Горький. Дело с застежками.

Ср. В руках двух палат - депутатов и пэров - сосредоточиваются важнейшие функции государственного управления.

А.Д. Градовский. Парламентаризм во Франции. 7.

Ср. Такие люди, как вы (свежие, можно сказать)... должны принимать на себя общественные функции...

Б.М. Маркевич. Бездна. 3, 12.

Ср. Fonction - functio - должность.

Ср. Functio (fungi, исполнять) - исполнение.

Ср. Fungi (functum) - исполнять.

фу́нкция, -и

фу́нкция, -и

фу́нкция, фу́нкции, фу́нкций, фу́нкциям, фу́нкцию, фу́нкцией, фу́нкциею, фу́нкциями, фу́нкциях

сущ., кол-во синонимов: 49

1. см. работа 1.

2. см. назначение.

3. см. обязанности

См. занятие...

1.

Syn: назначение

2.

Syn: выражение, связка

функция (лат. functio - отправление, исполнение]

1) Назначение; роль;

2) в лингвистике Ф.отражает соответствие между формой и значением языковых единиц. Целевая установка речи, потенциальная предназначенность языка в целом и отдельных его единиц для выполнения определенных целей.

функция (от лат. functio - деятельность, исполнение).

1) Роль, выполняемая языковой единицей (грамматической категорией, грамматической формой) при воспроизведении в речи. Функция сказуемого, выполняемая глаголом. Функция обстоятельства, выполняемая наречием. Функции именительного падежа существительных. Синтаксическая функция союзов.

2) Назначение (применение, использование) разных сторон языка и его элементов. Функция сообщения. Номинативная функция слова. см. функции слова, функции языка.

См. funzione.

фу́нкци/я [й/а].

фу́нкция ж 7a

возложить функции => перемещение / передача

выполнять функцию => действие

осуществлять функции => реализация

передать функции => перемещение / передача

разделить функции => совместность

функции выполнять => действие

Заимств. в XVIII в. из лат. яз., где functio «исполнение, функция» - суф. производное от fungi «осуществлять, исполнять».

ФУНКЦИЯ и, ж., ФОНКЦИЯ и, ж.fonction f. , пол. funcya <, лат. functio.

1.Фонкция. Должность. Курганов. Кардинал Аквавива управляющий здесь фонкции или дела гишпанского министра, торжествовал в прошлои вторник со многочисленною свитою праздник святаго Иакова в церкве сего имени. Вед. 1719 2 312. За болезнью господина канцлера .. токмо для фонкции и ответа на речи господина Понятовского ездил во дворец. 1756. АВ 33 220. Во всех публичных фонкциях помянутой Министр должен следовать безпосредственно за Цесарским Министром. 1774. ПСЗ 19 960. Служба наша приятна и видна, но не скоро полезна бывает, а представлять у двора приличную функции фигуру довольно подобно иждивения в таком месте, где что шаг ступить то и платить надобно. 1778. А. Безбородко. // РИО 26.

2. физиол. Проявление жизнедеятельности организма, тканей, клеток и т. п. БАС-1. Постоянно удивляться, постоянно находиться в процессе восхищения и восторга, это не жизнь, а некая особенная деятельность, специальное отправление (fonction) души. 25. 6. 1865. А. Ф. Тютчева. // И. Аксаков Письма 4 (1) 125.

3. Явление, зависящее от другого, основного явления и служащее формой его проявления, осуществления. БАС-1. < Литератора> терпят, на смотрят с снисходительным состраданием потому единственно, что литература в целом мире признается как одна из функций общественного бытия. Салт. Признаки времени. Без такого накопленного жизненного материала трудно будет разрешить безошибочно столь важное явление народной жизни со всеми его функциями. ВО 1882 2 4. - Лекс. Ян. 1806: функция; САН 1847: фу/нкция; СИЗ: функция 1707, фунция 1707, фунцион 1707.

ФУНКЦИЯ (лат. functio). В физиологии: отправление каким-либо органом ему одному свойственных действий, как напр., дыхание, пищеварение. 2) в математике: величина, зависящая от другой переменной величины.

- Математический статус синуса.

- Переменная величина, зависящая от значений другой.

- Тангенс по сути.

Составить слова из слова функция