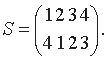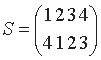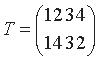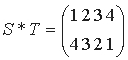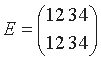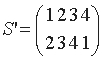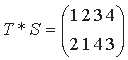Математику обычно определяют, перечисляя названия некоторых из ее традиционных разделов. Прежде всего, это арифметика, которая занимается изучением чисел, отношений между ними и правил действий над числами. Факты арифметики допускают различные конкретные интерпретации; например, соотношение 2 + 3 = 4 + 1 соответствует утверждению, что две и три книги составляют столько же книг, сколько четыре и одна. Любое соотношение типа 2 + 3 = 4 + 1, т.е. отношение между чисто математическими объектами без ссылки на какую бы то ни было интерпретацию из физического мира, называется абстрактным. Абстрактный характер математики позволяет использовать ее при решении самых разных проблем. Например, алгебра, рассматривающая операции над числами, позволяет решать задачи, выходящие за рамки арифметики. Более конкретным разделом математики является геометрия, основная задача которой - изучение размеров и форм объектов. Сочетание алгебраических методов с геометрическими приводит, с одной стороны, к тригонометрии (первоначально посвященной изучению геометрических треугольников, а теперь охватывающей значительно больший круг вопросов), а с другой стороны - к аналитической геометрии, в которой геометрические тела и фигуры исследуются алгебраическими методами. Существуют несколько разделов высшей алгебры и геометрии, обладающих более высокой степенью абстракции и не занимающихся изучением обычных чисел и обычных геометрических фигур; самая абстрактная из геометрических дисциплин называется топологией.
Математический анализ занимается изучением величин, изменяющихся в пространстве или во времени, и опирается на два основных понятия - функцию и предел, которые не встречаются в более элементарных разделах математики. Первоначально математический анализ состоял из дифференциального и интегрального исчислений, но теперь включает в себя и другие разделы. Различают две основные области математики - чистую математику, в которой акцент делается на дедуктивные рассуждения, и прикладную математику. Термин "прикладная математика" иногда относят к тем ветвям математики, которые созданы специально для того, чтобы удовлетворить запросы и требования науки, а иногда - к тем разделам различных наук (физики, экономики и т.п.), которые используют математику как средство решения своих задач.
Многие распространенные заблуждения в отношении математики возникают в результате смешения этих двух толкований "прикладной математики". Арифметика может служить примером прикладной математики в первом смысле, а бухгалтерский учет - во втором. Вопреки широко распространенному мнению, математика продолжает быстро развиваться. Журнал "Математическое обозрение" ("Mathematical Review") публикует ежегодно ок. 8000 кратких резюме статей, содержащих последние результаты - новые математические факты, новые доказательства старых фактов и даже сведения о совершенно новых областях математики. Существующая ныне тенденция в математическом образовании заключается в стремлении познакомить учащихся с современными, более абстрактными математическими идеями на более ранних стадиях преподавания математики.
См. также МАТЕМАТИКИ ИСТОРИЯ.
Математика - один из краеугольных камней цивилизации, однако очень немногие люди имеют представление о современном состоянии дел в этой науке. Математика за последние сто лет претерпела огромные изменения, касающиеся как предмета, так и методов исследования. В данной статье мы попытаемся дать общее представление об основных этапах эволюции современной математики, главными результатами которой можно считать, с одной стороны, увеличение разрыва между чистой и прикладной математикой, а с другой - полное переосмысление традиционных областей математики.
РАЗВИТИЕ МАТЕМАТИЧЕСКОГО МЕТОДА
Рождение математики. Около 2000 до н.э. было замечено, что в треугольнике со сторонами в 3, 4 и 5 единиц длины один из углов равен 90° (это наблюдение позволяло легко строить прямой угол для практических надобностей). Заметили ли тогда соотношение 52 = 32 + 42? Относительно этого мы не располагаем никакими сведениями. Через несколько веков было открыто общее правило: в любом треугольнике ABC с прямым углом при вершине A и сторонами b = АС и c = AB, между которыми заключен этот угол, и противолежащей ему стороной a = BC справедливо соотношение a2 = b2 + c2. Можно сказать, что наука начинается тогда, когда масса отдельных наблюдений объясняется одним общим законом; следовательно, открытие "теоремы Пифагора" можно рассматривать как один из первых известных примеров подлинно научного достижения.
Но еще более важное значение для науки вообще и для математики в частности имеет то, что наряду с формулировкой общего закона появляются попытки его доказать, т.е. показать, что он с необходимостью следует из других геометрических свойств. Одно из восточных "доказательств" особенно наглядно в своей простоте: четыре треугольника, равные данному, вписаны в квадрат BCDE так, как показано на чертеже. Площадь квадрата a2 оказывается разделенной на четыре равных треугольника общей площадью 2bc и квадрат AFGH площадью (b - c)2. Таким образом, a2 = (b - c)2 + 2bc = (b2 + c2 - 2bc) + 2bc = b2 + c2. Поучительно сделать еще один шаг и выяснить точнее, какие "предыдущие" свойства предполагаются известными. Наиболее очевидный факт заключается в том, что, поскольку треугольники BAC и BEF точно, без пробелов и наложения, "подогнаны" вдоль сторон BA и BF, это означает, что два угла при вершинах B и С в треугольнике ABС составляют вместе угол в 90° и поэтому сумма всех трех его углов равна 90° + 90° = 180°. В приведенном выше "доказательстве" используется также формула (bc/2) для площади треугольника ABC с углом в 90° при вершине A. Фактически были использованы и другие допущения, но и сказанного достаточно, чтобы мы могли наглядно увидеть существенный механизм математического доказательства - дедуктивное рассуждение, позволяющее с помощью чисто логических аргументов (на основе надлежащим образом подготовленного материала, в нашем примере - разбиения квадрата) вывести из известных результатов новые свойства, как правило, не следующие непосредственно из имеющихся данных.
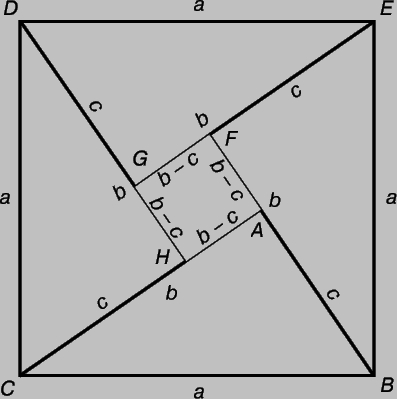
Рис. 1.
Аксиомы и методы доказательства. Одной из фундаментальных особенностей математического метода является процесс создания с помощью тщательно выстроенных чисто логических аргументов цепочки утверждений, в которой каждое последующее звено соединено с предыдущими. Первое достаточно очевидное соображение состоит в том, что в любой цепочке должно быть первое звено. Это обстоятельство стало очевидно грекам, когда они приступили к систематизации свода математических аргументов в 7 в. до н.э. Для осуществления этого замысла грекам понадобилось ок. 200 лет, и сохранившиеся документы позволяют составить лишь примерное представление о том, как именно они действовали. Точной информацией мы располагаем лишь об окончательном результате исследований - знаменитых Началах Евклида (ок. 300 до н.э.). Евклид начинает с перечисления исходных положений, из которых все остальные выводятся чисто логическим путем. Эти положения называются аксиомами или постулатами (термины практически взаимозаменяемые); они выражают либо весьма общие и несколько расплывчатые свойства объектов любого рода, например "целое больше части", либо какие-то конкретные математические свойства, например, что для любых двух точек существует единственная соединяющая их прямая. У нас нет никакой информации и о том, придавали ли греки некий более глубокий смысл или значимость "истинности" аксиом, хотя существуют кое-какие намеки, что, прежде чем принять те или иные аксиомы, греки некоторое время их обсуждали. У Евклида и его последователей аксиомы представлены лишь как исходные пункты для построения математики без всяких комментариев об их природе. Что касается методов доказательства, то они, как правило, сводились к прямому использованию ранее доказанных теорем. Иногда, правда, логика рассуждений оказывалась более сложной. Мы упомянем здесь излюбленный метод Евклида, вошедший в повседневную практику математики, - косвенное доказательство, или доказательство от противного. В качестве элементарного примера доказательства от противного покажем, что шахматную доску, из которой вырезаны два угловых поля, расположенных на противоположных концах диагонали, невозможно покрыть костями домино, каждая из которых равна двум полям. (Предполагается, что каждое поле шахматной доски должно быть покрыто только один раз.) Предположим, что верно противоположное ("противное") утверждение, т.е. что доску можно покрыть костями домино. Каждая кость покрывает одно черное и одно белое поле, поэтому независимо от расположения костей домино они покрывают равное число черных и белых полей. Однако из-за того, что два угловых поля удалены, шахматная доска (на которой первоначально было столько же черных полей, сколько белых) имеет полей одного цвета на два больше, чем полей другого цвета. Это означает, что наше исходное предположение не может быть истинным, так как приводит к противоречию. А поскольку противоречащие друг другу суждения не могут быть ложными одновременно (если одно из них ложно, то противоположное истинно), наше исходное предположение должно быть истинным, ибо противоречащее ему предположение ложно; следовательно, шахматную доску с двумя вырезанными угловыми полями, расположенными по диагонали, невозможно покрыть костями домино. Итак, чтобы доказать некоторое утверждение, мы можем предположить, что оно ложно, и вывести из этого предположения противоречие с каким-нибудь другим утверждением, истинность которого известна. Прекрасный пример доказательства от противного, ставший одной из вех в развитии древнегреческой математики, - доказательство того, что - не рациональное число, т.е. непредставимо в виде дроби p/q, где p и q - целые числа. Если , то 2 = p2/q2, откуда p2 = 2q2. Предположим, что существуют два целых числа p и q, для которых p2 = 2q2. Иначе говоря, мы предполагаем, что существует целое число, квадрат которого вдвое больше квадрата другого целого числа. Если какие-нибудь целые числа удовлетворяют этому условию, то одно из них должно быть меньше всех других. Сосредоточим внимание на наименьшем из таких чисел. Пусть это будет число p. Так как 2q2 - четное число и p2 = 2q2, то число p2 должно быть четным. Так как квадраты всех нечетных чисел нечетны, а квадрат p2 четен, значит само число p должно быть четным. Иначе говоря, число p вдвое больше некоторого целого числа r. Так как p = 2r и p2 = 2q2, имеем: (2r)2 = 4r2 = 2q2 и q2 = 2r2. Последнее равенство имеет тот же вид, что и равенство p2 = 2q2, и мы можем, повторяя те же рассуждения, показать, что число q четно и что существует такое целое число s, что q = 2s. Но тогда q2 = (2s)2 = 4s2, и, поскольку q2 = 2r2, мы заключаем, что 4s2 = 2r2 или r2 = 2s2. Так мы получаем второе целое число, которое удовлетворяет условию, что его квадрат вдвое больше квадрата другого целого числа. Но тогда p не может быть наименьшим таким числом (поскольку r = p/2), хотя первоначально мы предполагали, что оно - наименьшее из таких чисел. Следовательно, наше исходное предположение ложно, так как приводит к противоречию, и поэтому не существует таких целых чисел p и q, для которых p2 = 2q2 (т.е. таких, что ). А это означает, что число не может быть рациональным. От Евклида до начала 19 в. На протяжении этого периода математика существенно преобразилась в результате трех новаций. (1) В процессе развития алгебры был изобретен способ символической записи, позволявший представлять в сокращенном виде все более сложные соотношения между величинами. В качестве примера тех неудобств, которые возникли бы, не будь такой "скорописи", попробуем передать словами соотношение (a + b)2 = a2 + 2ab + b2: "Площадь квадрата со стороной, равной сумме сторон двух данных квадратов, равна сумме их площадей вместе с удвоенной площадью прямоугольника, стороны которого равны сторонам данных квадратов". (2) Создание в первой половине 17 в. аналитической геометрии, давшей возможность любую задачу классической геометрии свести к некоторой алгебраической задаче. (3) Создание и развитие в период с 1600 по 1800 исчисления бесконечно малых, позволявшего легко и систематически решать сотни задач, связанных с понятиями предела и непрерывности, лишь очень немногие из которых были решены древнегреческими математиками. Более подробно эти ветви математики рассматриваются в статьях
АЛГЕБРА;
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ;
МАТЕМАТИЧЕСКИЙ АНАЛИЗ;
ГЕОМЕТРИИ ОБЗОР. Начиная с 17 в. постепенно проясняется вопрос, который до тех пор оставался неразрешимым. Что такое математика? До 1800 ответ был достаточно простым. В то время четких границ между различными науками не существовало, математика была частью "натуральной философии" - систематического изучения природы методами, предложенными великими реформаторами эпохи Возрождения и начала 17 в. - Галилеем (1564-1642), Ф.Бэконом (1561-1626) и Р.Декартом (1596-1650). Считалось, что у математиков имеется своя собственная область исследования - числа и геометрические объекты и что математики не пользуются экспериментальным методом. Однако Ньютон и его последователи изучали механику и астрономию с помощью аксиоматического метода по аналогии с тем, как была изложена геометрия у Евклида. В более общем плане было признано, что любая наука, в которой результаты эксперимента представимы с помощью чисел или систем чисел, становится областью приложения математики (в физике это представление утвердилось лишь в 19 в.). Области экспериментальной науки, которые подверглись математической обработке, часто называют "прикладной математикой"; это очень неудачное название, так как ни по классическим, ни по современным стандартам в этих приложениях не существует (в строгом смысле) подлинно математических аргументов, поскольку в них предметом исследования являются нематематические объекты. После того как данные эксперимента переведены на язык чисел или уравнений (такой "перевод" зачастую требует большой находчивости со стороны "прикладного" математика), появляется возможность широкого применения математических теорем; затем результат подвергается обратному переводу и сравнивается с наблюдениями. То, что к процессу такого рода применяется термин "математика", служит одним из источников нескончаемых недоразумений. В "классические" времена, о которых сейчас идет речь, такого рода недоразумений не существовало, поскольку одни и те же люди являлись и "прикладными", и "чистыми" математиками, занимаясь одновременно и проблемами математического анализа или теории чисел, и проблемами динамики или оптики. Однако усилившаяся специализация и тенденция к обособлению "чистой" и "прикладной" математик значительно ослабили ранее существовавшую традицию универсальности, и ученые, которые, подобно Дж.фон Нейману (1903-1957), были способны вести активную научную деятельность как в прикладной, так и в чистой математике, стали скорее исключением, чем правилом. Какова природа математических объектов - чисел, точек, линий, углов, поверхностей и т.д., существование которых мы считали чем-то само собою разумеющимся? Что означает применительно к таким объектам понятие "истина"? На эти вопросы в классический период были даны вполне определенные ответы. Разумеется, ученые той эпохи отчетливо понимали, что в мире наших ощущений нет таких вещей, как "бесконечно протяженная прямая" или "не имеющая размеров точка" Евклида, как нет "чистых металлов", "монохроматического света", "теплоизолированных систем" и т.д., которыми оперируют в своих рассуждениях экспериментаторы. Все эти понятия - "платоновские идеи", т.е. своего рода порождающие модели эмпирических понятий, хотя и радикально иного характера. Тем не менее молчаливо предполагалось, что физические "образы" идей могут быть сколь угодно близки к самим идеям. В той мере, в какой вообще можно что-либо утверждать относительно близости объектов к идеям, говорят, что "идеи" являются, так сказать, "предельными случаями" физических объектов. С этой точки зрения, аксиомы Евклида и выводимые из них теоремы выражают свойства "идеальных" объектов, которым должны соответствовать предсказуемые экспериментальные факты. Например, измерение оптическими методами углов треугольника, образованного тремя точками в пространстве, в "идеальном случае" должно дать сумму, равную 180°. Иначе говоря, аксиомы поставлены на один уровень с физическими законами, и поэтому их "истинность" воспринимается так же, как истинность физических законов; т.е. логические следствия из аксиом подлежат проверке путем сравнения с экспериментальными данными. Разумеется, согласие можно достичь лишь в пределах ошибки, связанной и с "несовершенным" характером измерительного прибора, и "несовершенной природой" измеряемого объекта. Однако всегда предполагается, что если законы "истинны", то усовершенствования процессов измерения в принципе позволяют сделать ошибку измерения сколь угодно малой. На протяжении 18 в. находилось все больше подтверждений того, что все следствия, полученные из основных аксиом, в особенности в астрономии и механике, согласуются с данными экспериментов. А поскольку эти следствия получались с использованием существовавшего в то время математического аппарата, достигнутые успехи способствовали укреплению мнения об истинности аксиом Евклида, которая, как говорил Платон, "ясна каждому" и не подлежит обсуждению.
Сомнения и новые надежды. Неевклидова геометрия. Среди постулатов, приведенных Евклидом, один был настолько неочевиден, что даже первые ученики великого математика считали его слабым местом в системе Начал. Аксиома, о которой идет речь, утверждает, что через точку, лежащую вне данной прямой, можно провести только одну прямую, параллельную данной прямой. Большинство геометров считали, что аксиому о параллельных можно доказать с помощью других аксиом и что Евклид сформулировал утверждение о параллельных как постулат просто потому, что ему не удалось придумать такое доказательство. Но, хотя лучшие математики пытались разрешить проблему параллельных, никому из них не удалось превзойти Евклида. Наконец, во второй половине 18 в. были предприняты попытки доказать постулат Евклида о параллельных от противного. Предположили, что аксиома о параллельных ложна. Априори постулат Евклида мог оказаться ложным в двух случаях: если через точку вне данной прямой невозможно провести ни одной параллельной; или если через нее можно провести несколько параллельных. Оказалось, что первая априорная возможность исключается другими аксиомами. Приняв вместо традиционной аксиомы о параллельных новую аксиому (о том, что через точку вне данной прямой можно провести несколько прямых, параллельных данной), математики пытались вывести из нее утверждение, противоречащее другим аксиомам, но потерпели неудачу: сколько они ни пытались извлекать следствий из новой "антиевклидовой", или "неевклидовой" аксиомы, противоречие так и не появилось. Наконец, независимо друг от друга Н.И.Лобачевский (1793-1856) и Я. Бойяи (1802-1860) поняли, что постулат Евклида о параллельных недоказуем, или, иначе говоря, в "неевклидовой геометрии" противоречие не появится. С появлением неевклидовой геометрии сразу же возникло несколько философских проблем. Поскольку претензия на априорную необходимость аксиом отпала, оставался единственный способ проверки их "истинности" - экспериментальный. Но, как позднее заметил А. Пуанкаре (1854-1912), в описании любого явления скрыто такое множество физических допущений, что ни один эксперимент не может дать убедительного доказательства истинности или ложности математической аксиомы. Кроме того, даже если допустить, что наш мир является "неевклидовым", следует ли из этого, что вся евклидова геометрия ложна? Насколько известно, ни один математик никогда не рассматривал такую гипотезу всерьез. Интуиция подсказывала, что и евклидова и неевклидова геометрии являются примерами полноценной математики.
Математические "монстры". Неожиданно к таким же выводам пришли совершенно с другой стороны - были открыты объекты, повергшие математиков 19 в. в шок и получившие название "математических монстров". Это открытие имеет непосредственное отношение к весьма тонким вопросам математического анализа, возникшим лишь в середине 19 в. Трудности возникли при попытке найти точный математический аналог экспериментальному понятию кривой. То, что было сутью понятия "непрерывного движения" (например, острия чертежного пера, движущегося по листу бумаги), подлежало точному математическому определению, и эта цель была достигнута, когда понятие непрерывности обрело строгий математический смысл (см. также КРИВАЯ) . Интуитивно казалось, что "кривая" в каждой своей точке имеет как бы направление, т.е. в общем случае в окрестности каждой своей точки кривая ведет себя почти так же, как прямая. (С другой стороны, нетрудно представить, что кривая имеет конечное число угловых точек, "изломов", как многоугольник.) Это требование могло быть сформулировано математически, а именно, предполагалось существование касательной к кривой, и до середины 19 в. считалось, что "кривая" имеет касательную почти во всех своих точках, быть может, за исключением некоторых "особых" точек. Поэтому открытие "кривых", не имевших касательной в любой своей точке, вызвало настоящий скандал
(см. также ФУНКЦИЙ ТЕОРИЯ).
(Читатель, знакомый с тригонометрией и аналитической геометрией, может легко проверить, что кривая, задаваемая уравнением y = x sin (1/x) , не имеет касательной в начале координат, но определить кривую, не имеющую касательной ни в одной своей точке, значительно сложнее.) Несколько позднее был получен куда более "патологический" результат: удалось построить пример кривой, которая полностью заполняет квадрат. С тех пор были изобретены сотни таких "монстров", противоречивших "здравому смыслу". Следует подчеркнуть, что существование столь необычных математических объектов следует из основных аксиом столь же строго и логически безупречно, как существование треугольника или эллипса. Поскольку математические "монстры" не могут соответствовать никакому экспериментальному объекту, и единственное возможное заключение состоит в том, что мир математических "идей" гораздо богаче и необычнее, чем можно было ожидать, и лишь очень немногие из них имеют соответствия в мире наших ощущений. Но если математические "монстры" логически следуют из аксиом, то можно ли по-прежнему считать аксиомы истинными?
Новые объекты. Приведенные выше результаты получили подтверждение еще с одной стороны: в математике, главным образом в алгебре, один за другим стали возникать новые математические объекты, представлявшие собой обобщения понятия числа. Обычные целые числа достаточно "интуитивны", и придти к экспериментальному понятию дроби совсем не трудно (хотя нельзя не признать, что операция деления единицы на несколько равных частей и выбор нескольких из них по своей природе отличаются от процесса счета). После того как выяснилось, что число непредставимо в виде дроби, греки были вынуждены рассматривать иррациональные числа, корректное определение которых с помощью бесконечной последовательности приближений рациональными числами принадлежит к наивысшим достижениям человеческого разума, но вряд ли соответствует чему-нибудь реальному в нашем физическом мире (где любое измерение неизменно сопряжено с ошибками). Тем не менее введение иррациональных чисел происходило более или менее в духе "идеализации" физических понятий. А что сказать об отрицательных числах, которые медленно, встречая большое сопротивление, стали входить в научный обиход в связи с развитием алгебры? Со всей определенностью можно утверждать, что не было никаких готовых физических объектов, отправляясь от которых мы с помощью процесса прямой абстракции могли бы выработать понятие отрицательного числа, и в преподавания элементарного курса алгебры приходится вводить множество вспомогательных и достаточно сложных примеров (ориентированные отрезки, температуры, долги и т.д.), чтобы пояснить, что такое отрицательные числа. Такое положение очень далеко от понятия, "ясного каждому", как того требовал Платон от идей, лежащих в основе математики, и нередко приходится встречать выпускников колледжей, для которых все еще остается загадкой правило знаков (-a)(-b) = ab. См. также ЧИСЛО. Еще хуже обстоит дело с "мнимыми", или "комплексными" числами, поскольку в них входит "число" i, такое, что i2 = -1, что является явным нарушением правила знаков. Тем не менее математики с конца 16 в. не колеблясь производят вычисления с комплексными числами, как если бы они "имели смысл", хотя 200 лет назад не могли дать определения этих "объектов" или интерпретировать их с помощью какой-либо вспомогательной конструкции, как, например, были интерпретированы с помощью направленных отрезков отрицательные числа. (После 1800 было предложено несколько интерпретаций комплексных чисел, самая известная - с помощью векторов на плоскости.)
Современная аксиоматика. Переворот произошел во второй половине 19 в. И хотя он не сопровождался принятием официальных заявлений, в действительности речь шла именно о провозглашении своего рода "декларации независимости". Конкретнее - о провозглашении де факто декларации независимости математики от внешнего мира. С этой точки зрения, математические "объекты", если вообще имеет смысл говорить об их "существовании", - чистое порождение разума, и имеют ли они какие-нибудь "соответствия" и допускают ли какую-нибудь "интерпретацию" в физическом мире, для математики несущественно (хотя сам по себе этот вопрос интересен). "Истинные" утверждения о таких "объектах" - все те же логические следствия из аксиом. Но теперь аксиомы следует рассматривать как совершенно произвольные, и поэтому отпадает необходимость в их "очевидности" или выводимости из повседневного опыта посредством "идеализации". На практике полная свобода ограничена разного рода соображениями. Разумеется, "классические" объекты и их аксиомы остаются без изменений, но теперь их нельзя считать единственными объектами и аксиомами математики, и в повседневную практику вошла привычка выбрасывать или переделывать аксиомы так, чтобы была возможность использовать их различными способами, как это было сделано при переходе от евклидовой геометрии к неевклидовой. (Именно таким образом были получены многочисленные варианты "неевклидовых" геометрий, отличных от евклидовой геометрии и от геометрии Лобачевского - Бойяи; например, имеются неевклидовы геометрии, в которых не существует параллельных прямых.) Хотелось бы особенно подчеркнуть одно обстоятельство, следующее из нового подхода к математическим "объектам": все доказательства должны опираться исключительно на аксиомы. Если мы вспомним об определении математического доказательства, то подобное высказывание может показаться повтором. Однако это правило редко соблюдалось в классической математике из-за "интуитивной" природы ее объектов или аксиом. Даже в Началах Евклида, при всей их кажущейся "строгости", многие аксиомы не формулируются явно и многие свойства либо молчаливо предполагаются, либо вводятся без достаточного обоснования. Чтобы поставить евклидову геометрию на прочную основу, понадобился критический пересмотр самих ее начал. Вряд ли стоит говорить о том, что педантичный контроль за мельчайшими деталями доказательства является следствием появления "монстров", научивших современных математиков соблюдать крайнюю осторожность в выводах. Самое безобидное и "самоочевидное" утверждение о классических объектах, например утверждение о том, что кривая, соединяющая точки, расположенные по разные стороны от прямой, непременно пересекает эту прямую, в современной математике требует строгого формального доказательства. Возможно, покажется парадоксальным утверждение, что именно из-за своей приверженности аксиомам современная математика служит наглядным примером того, какой должна быть любая наука. Тем не менее такой подход иллюстрирует характерную особенность одного из наиболее фундаментальных процессов научного мышления - получения точной информации в ситуации неполного знания. Научное исследование некоторого класса объектов предполагает, что особенности, позволяющие отличать одни объекты от других, умышленно предаются забвению, а сохраняются лишь общие черты рассматриваемых объектов. То, что выделяет математику из общего ряда наук, заключается в неукоснительном следовании этой программе во всех ее пунктах. Считается, что математические объекты полностью определены аксиомами, используемыми в теории этих объектов; или, по словам Пуанкаре, аксиомы служат "замаскированными определениями" тех объектов, к которым они относятся.
СОВРЕМЕННАЯ МАТЕМАТИКА
Хотя теоретически возможно существование любых аксиом, до настоящего времени было предложено и исследовано лишь небольшое число аксиом. Обычно в ходе развития одной или нескольких теорий замечают, что какие-то схемы доказательства повторяются в более или менее аналогичных условиях. После того как свойства, используемые в общих схемах доказательств, обнаружены, их формулируют в виде аксиом, а следствия из них выстраивают в общую теорию, не имеющую прямого отношения к тем конкретным контекстам, из которых были абстрагированы аксиомы. Получаемые при этом общие теоремы применимы к любой математической ситуации, в которой существуют системы объектов, удовлетворяющие соответствующим аксиомам. Повторяемость одних и тех же схем доказательства в различных математических ситуациях свидетельствует о том, что мы имеем дело с различными конкретизациями одной и той же общей теории. Это означает, что после соответствующей интерпретации аксиомы этой теории в каждой ситуации становятся теоремами. Любое свойство, выводимое из аксиом, будет справедливо во всех этих ситуациях, но необходимость в отдельном доказательстве для каждого случая отпадает. В таких случаях говорят, что математические ситуации обладают одной и той же математической "структурой". Мы пользуемся представлением о структуре на каждом шагу в нашей повседневной жизни. Если термометр показывает 10° С и бюро прогнозов предсказывает повышение температуры на 5° С, мы без всяких вычислений ожидаем температуру в 15° С. Если книга открыта на 10-й странице и нас просят заглянуть на 5 страниц дальше, мы не колеблясь открываем ее на 15-й странице, не отсчитывая промежуточных страниц. В обоих случаях мы полагаем, что сложение чисел дает правильный результат независимо от их интерпретации - в виде температуры или номеров страниц. Нам нет нужды учить одну арифметику для термометров, а другую - для номеров страниц (хотя мы пользуемся особой арифметикой, имея дело с часами, в которой 8 + 5 = 1, так как часы обладают другой структурой, чем страницы книги). Интересующие математиков структуры отличаются несколько более высокой сложностью, в чем нетрудно убедиться на примерах, разбору которых посвящены два следующих раздела данной статьи. В одном из них речь пойдет о теории групп и математических понятиях структур и изоморфизмов.
Теория групп. Чтобы лучше понять процесс, обрисованный выше в общих чертах, возьмем на себя смелость заглянуть в лабораторию современного математика и присмотреться к одному из его основных инструментов - теории групп
(см. также АЛГЕБРА АБСТРАКТНАЯ).
Группой называется набор (или "множество") объектов G, на котором определена операция, ставящая в соответствие любым двум объектам или элементам a, b из G, взятым в указанном порядке (первым - элемент a, вторым - элемент b), третий элемент c из G по строго определенному правилу. Для краткости обозначим этот элемент a*b; звездочка (*) означает операцию композиции двух элементов. Эта операция, которую мы назовем групповым умножением, должна удовлетворять следующим условиям: (1) для любых трех элементов a, b, c из G выполняется свойство ассоциативности: a* (b*c) = (a*b) *c; (2) в G существует такой элемент e, что для любого элемента a из G имеет место соотношение e*a = a*e = a; этот элемент e называется единичным или нейтральным элементом группы; (3) для любого элемента a из G найдется такой элемент a', называемый обратным или симметричным к элементу a, что a*a' = a'*a = e. Если эти свойства принять за аксиомы, то логические следствия из них (независимые от каких-либо других аксиом или теорем) в совокупности образуют то, что принято называть теорией групп. Вывести раз и навсегда эти следствия оказалось очень полезно, поскольку группы широко применяются во всех разделах математики. Из тысяч возможных примеров групп выберем лишь несколько наиболее простых. (а) Дроби p/q, где p и q - произвольные целые числа і1 (при q = 1 мы получаем обыкновенные целые числа). Дроби p/q образуют группу относительно группового умножения (p/q) *(r/s) = (pr)/(qs). Свойства (1), (2), (3) следуют из аксиом арифметики. Действительно, [[(p/q) *(r/s)]] *(t/u) = (prt)/(qsu) = (p/q)*[[(r/s)*(t/u)]]. Единичным элементом служит число 1 = 1/1, так как (1/1)*(p/q) = (1*p)/(1*q) = p/q. Наконец, элементом, обратным к дроби p/q, является дробь q/p, так как (p/q)*(q/p) = (pq)/(pq) = 1.
(b) Рассмотрим в качестве G набор из четырех целых чисел 0, 1, 2, 3, а в качестве a*b - остаток от деления a + b на 4. Результаты таким образом введенной операции представлены в табл. 1 (элемент a*b стоит на пересечении строки a и столбца b). Нетрудно проверить, что свойства (1)-(3) выполняются, а единичным элементом служит число 0.
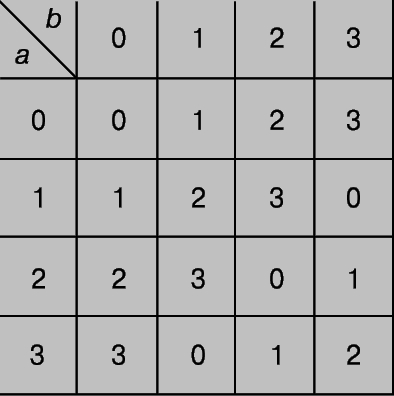
Таблица 1.
(с) Выберем в качестве G набор чисел 1, 2, 3, 4, а в качестве a*b - остаток от деления ab (обычного произведения) на 5. В результате получим табл. 2. Легко проверить, что свойства (1)-(3) выполняются, а единичным элементом служит 1.
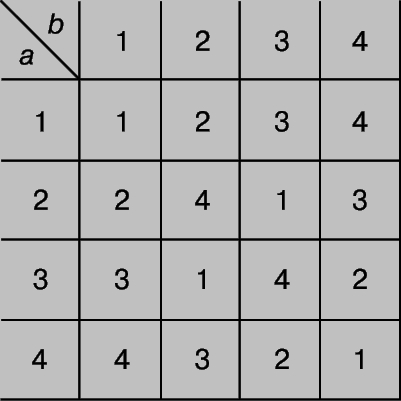
Таблица 2.
(d) Четыре объекта, например четыре числа 1, 2, 3, 4, можно расположить в ряд 24 способами. Каждое расположение можно наглядно представить как преобразование, переводящее "естественное" расположение в заданное; например, расположение 4, 1, 2, 3 получается в результате преобразования S: 1 -> 4, 2 -> 1, 3 -> 2, 4 -> 3,
которое можно записать в более удобном виде
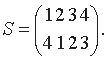
Для любых двух таких преобразований S, T мы определим S*T как преобразование, которое получится в результате
последовательного выполнения Т, а затем S.
Например, если
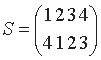
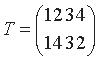
, то
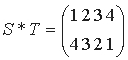
При таком определении все 24 возможных преобразования образуют группу; ее единичным элементом служит
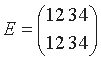
, а элемент, обратный к S, получается при замене стрелок в определении S на противоположные;
например, если
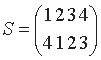
, то
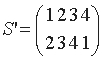
Нетрудно заметить, что в первых трех примерах a*b = b*a; в таких случаях говорят, что группа или групповое умножение
коммутативны. С другой стороны, в последнем примере
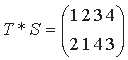
, и, следовательно, T*S отличается от S*T.
Группа из примера (d) является частным случаем т.н. симметрической группы, в сферу приложений которой входят,
среди прочего, методы решения алгебраических уравнений и поведение линий в спектрах атомов.
Группы из примеров (b) и (c) играют важную роль в теории чисел; в примере (b) число 4 можно заменить любым целым
числом n, а числа от 0 до 3 - числами от 0 до n - 1 (при n = 12 мы получим систему чисел, которые стоят на
циферблатах часов, о чем мы упоминали выше); в примере (с) число 5 можно заменить любым простым числом р,
а числа от 1 до 4 - числами от 1 до p - 1.
Структуры и изоморфизм. Предыдущие примеры показывают, сколь разнообразной может быть природа объектов, образующих группу. Но на самом деле в каждом случае все сводится к одному и тому же сценарию: из свойств множества объектов мы рассматриваем лишь те, которые превращают это множество в группу