ДИФФЕР а, м. différentiel m. разг. То же, что диференциал (дифференциальная коробка автомобиля). Цистерна тронулась и через десять шагов сползла в болото.. Машина села на диффер, и положение ее было безнадежно. 1941. В. М. Шпейер Восп. // ОА 2001 3 45. Ср. также Дифференциал 2. - Норм. "Дифер" вместо "дифференциал". Лотте 1932.

Составить слова из слова диффер

ДИФФЕР|А (2*), -Ы с. διφθέρα Короткая риза, надеваемая на поставляемых в церковный клир:

малы˫а же ризица гл҃тьсѩ грьчьскы||мь ˫азыкомь. диффера. или фелонь. КН 1280, 546а-б; то же КР 1284, 80б.

Составить слова из слова диффера

I.

ДИФФЕРАНС I différence f. Различие. Джюре, написавший автобиографическую повесть .. было проще: она, зная и даже подчеркивая свою différence и требуя уважения ее права на différence, сама и выбирает. Восток 1997 4 64.

II.

ДИФФЕРАНС II différance f. < différence f. различие. Понятия, которыми оперирует постмодернизм .. "симулякрум" .. "différance"( = и обозначение, и его отсроченность), "écriture" ( = и наличие, и неданность отправителя сообщения). И. П. Смирнов Теория и революция. // НЛО 1997 23 44. Сходным образом строится аргументация против классического идеала рациональности и в постструктурализме (жюль Делёз, Жак Деррида, Жан-Франсуа Лиотар). Здесь тоже речь идет о противостонии "мышления идентичности" - с этой целью упомянутые авторы разрабатывают понятие "различие (différence), а Деррида придумывает неологизм différance - слово, указывающее на различие весьма элегантным для слуха образом ( a вместо e неуловимо для слуха, видно на письме). Именно различию принадлежит приоритет перед тожддеством, говорят французские философы. В. с. Малахов Война культур. // Октябрь 1997 7 151.

Составить слова из слова дифферанс

I м.

Разница в осадке (углублении) носа и кормы корабля; угол продольного наклона судна (в морском деле).

II м.

Разница в цене товара при его заказе и при получении (в торговых операциях).

ДИФФЕРЕНТ - муж., мор. разность огрузки кормы и носа; разногруз, разносадка. Дифферент пускается на корму, огрузка кормы бывает глубже. Дифференциал муж., мат. бесконечно малое количество. Дифференциальное вычисление, способ вычисления посредством бесконечно малых величин. Дифференциальное деление, на термометре или другом снаряде, самое мелкое, точное. Дифференцировать величину, мат. искать разности величин, количеств дифференциальным способом.

ДИФФЕРЕ́НТ -а; м. [лат. differens]

1. Спец. Разница в осадке носа и кормы судна.

2. Финанс. Разница в цене на товар при заказе и получении его в процессе торговых операций.

* * *

диффере́нт (от лат. differens - разница), разница в осадке (углублении) судна носом и кормой.

* * *

ДИФФЕРЕНТ - ДИФФЕРЕ́НТ (от лат. differens - разница), разница в осадке (углублении) судна носом и кормой.

ДИФФЕРЕНТ (от лат. differens - разница) - разница в осадке (углублении) судна носом и кормой.

диффере́нт, -а (тех.; фин.)

диффере́нт (наклон судна)

диффере́нт, диффере́нты, диффере́нта, диффере́нтов, диффере́нту, диффере́нтам, диффере́нтом, диффере́нтами, диффере́нте, диффере́нтах

сущ., кол-во синонимов: 1

наклон

диффере́нт/ (наклон судна).

диффере́нт м 1a (в торговле; в кораблевождении)

ДИФФЕРЕНТ, ДИФЕРЕНТ а, м. différent m. <лат. differens (ntis различающийся.

1. мор. Разница погружения кормы и носа корабля. Сл. 18. В конце журнала пишут состояние корабля в ходу, как то диферент груза, то есть на сколько фут разнится форштевень с ахтерштевенем. Навиг. (б) 205. Каждому Капитану старатся привести свой корабль в самый лучший диферент, дабы чрез то выиграть у неприятеля ветр. Куш. МС 2 310. // Сл. 18. Если углубление носа больше, чем углубление кормы. то судно имеет дифферент на нос, и наоборот. СИС 1954.

2. Разница в цене на товар при заказе и при получении его. СИС 1954. - Лекс. Ян. 1803: дифферент; САН 1847: диффере/нт; Сл. 18: диферент 1764 (диффе- 1803).

ДИФФЕРЕНТ (лат., от differe - различать). Разность глубины погружения в воду кормы и носа корабля.

- Наклон судна на нос или в корму.

- Разница в цене за товар при заказе и при получении его.

Составить слова из слова дифферент

сущ., кол-во синонимов: 1

Тоже, что детерминизм.

Составить слова из слова дифферентизм

сущ., кол-во синонимов: 1

Составить слова из слова дифферентование

сущ., кол-во синонимов: 1

дифферентование

Составить слова из слова дифферентовка

дифференто́метр, -а

дифференто́метр

дифференто́метр, дифференто́метры, дифференто́метра, дифференто́метров, дифференто́метру, дифференто́метрам, дифференто́метром, дифференто́метрами, дифференто́метре, дифференто́метрах

дифферент/о́/метр/.

дифференто́метр м 1a

Составить слова из слова дифферентометр

I м.

Произвольное приращение независимой переменной величины; главная - линейная - часть приращения зависимой переменной величины, пропорциональная приращению независимой переменной (в математике).

II м.

Устройство, обеспечивающее вращение с разными скоростями ведущих колес автомобиля, трактора и т.п. при поворотах (в технике).

ДИФФЕРЕНЦИА́Л, -а, муж.

1. В математике: линейная функция, приближенно равная нек-рой функции в окрестности какой-н. точки. Д. функции.

2. Механизм, дающий возможность расположенным на одной оси колёсам, вращающимся деталям двигаться с разной скоростью для совместной работы (спец.).

| прил. дифференциальный, -ая, -ое (к 1 знач.). Дифференциальное исчисление. Дифференциальное уравнение.

ДИФФЕРЕНЦИА́Л -а; м. [от лат. differentia - разность]

1. Матем. Главная линейная часть приращения зависимой переменной величины (функции), приближённо выражающая значение этого приращения; приращение независимой переменной величины. Нахождение дифференциалов.

2. Техн. Механизм, обеспечивающий вращение ведущих колёс транспорта с различной скоростью при поворотах. Регулировка дифференциала.

* * *

дифференциал - I

(от лат. differentia - разность, различие), см. Дифференциальное исчисление.

II

название дифференциального механизма в приводе ведущих колёс автомобиля, трактора или других колёсных машин. Наиболее распространён дифференциал с коническими зубчатыми колёсами.

ДИФФЕРЕНЦИАЛ - название дифференциального механизма в приводе ведущих колес автомобиля, трактора или других колесных машин. Наиболее распространен дифференциал с коническими зубчатыми колесами.

-----------------------------------

ДИФФЕРЕНЦИАЛ (от лат. differentia - разность - различие), см. Дифференциальное исчисление.

-а, м.

1. мат.

Главная линейная часть приращения зависимой переменной величины (функции), приближенно выражающая значение этого приращения, а также приращение независимой переменной величины.

2. тех.

Механизм в автомобилях, тракторах, танках и т. п., позволяющий правому и левому ведущим колесам вращаться с различной скоростью.

[От лат. differentia - разность]

ДИФФЕРЕНЦИАЛ (от латинского differentia - разность, различие), одно из основных понятий дифференциального исчисления.

дифференциа́л, -а

дифференциа́л

дифференциа́л, дифференциа́лы, дифференциа́ла, дифференциа́лов, дифференциа́лу, дифференциа́лам, дифференциа́лом, дифференциа́лами, дифференциа́ле, дифференциа́лах

сущ., кол-во синонимов: 2

дифференци/а́л/.

дифференциа́л м 1a

ДИФФЕРЕНЦИАЛ а, м. différentiel m. , нем. Differenzial < differentia разность.

1. В математике - произвольное приращение независимой переменной величины; главная (линейная) часть приращения зависимой переменной величины, пропорциональная приращению независмой переменной. БАС-2. Возьми дифференциял сего уравнения. Кот. геодет 147. // Сл. 18. Иной читатель спросит: " а что же доказано этим?" - спросит, как спрашивал один французский математик после представления какой-то драмы, в которой он не нашел ни уравнений. ни дифференциалов. 1848. Т. И. Кокорев Чай в Москве. // Очерк 448.

2. В технике - механизм, обеспечивающий вращение с разными скоростями ведущих колес автомобиля. трактора и т. п. при поворотах. БАС-2. - Лекс. Энц. лекс. 1839: дифференциал; САН 1847: дифференциа/л.

ДИФФЕРЕНЦИАЛ (лат., от differe - различать). Предел бесконечно малой разности между функцией переменного, получившего бесконечно малое приращение, и первоначальной функцией того же переменного (мат. терм.).

- Устройство для передачи крутящего момента в приводе ведущих колёс.

- Часть трансмиссии.

- В математике именно так называется бесконечно малая разность значений переменной величины.

Составить слова из слова дифференциал

ДИФФЕРЕНЦИАЛ (в автомобильном деле) - ДИФФЕРЕНЦИА́Л, название дифференциального механизма в приводе ведущих колес автомобиля, трактора или других колесных машин. Наиболее распространен дифференциал с коническими зубчатыми колесами.

Составить слова из слова дифференциал (в автомобильном деле)

ДИФФЕРЕНЦИАЛ (см. Дифференциальное исчисление) - ДИФФЕРЕНЦИА́Л (от лат. differentia - разность, различие), см. Дифференциальное исчисление (см. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ).

Составить слова из слова дифференциал (см. дифференциальное исчисление)

Дифференциа́льная геоме́трия - раздел геометрии, в которой геометрические образы изучаются на основе метода координат средствами дифференциального исчисления. Первоначально предметом дифференциальной геометрии было изучение геометрических образов обычного трёхмерного пространства (линий, поверхностей). Со второй половины XIX в. рамки дифференциальной геометрии значительно расширились; в неё включается также изучение так называемых многомерных пространств. Дифференциальная геометрия - важное орудие исследования в механике, теории относительности и др.

* * *

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ - ДИФФЕРЕНЦИА́ЛЬНАЯ ГЕОМЕ́ТРИЯ, раздел геометрии, в которой геометрические образы изучаются на основе метода координат средствами дифференциального исчисления. Первоначально предметом дифференциальной геометрии было изучение геометрических образов обычного трехмерного пространства (линий, поверхностей). Со 2-й пол. 19 в. рамки дифференциальной геометрии значительно расширились, включив также изучение т. н. многомерных пространств. Дифференциальная геометрия - важное орудие исследования в механике, теории относительности и др.

ДИФФЕРЕНЦИАЛЬНАЯ геометрия - раздел геометрии, в которой геометрические образы изучаются на основе метода координат средствами дифференциального исчисления. Первоначально предметом дифференциальной геометрии было изучение геометрических образов обычного трехмерного пространства (линий, поверхностей). Со 2-й пол. 19 в. рамки дифференциальной геометрии значительно расширились, включив также изучение т. н. многомерных пространств. Дифференциальная геометрия - важное орудие исследования в механике, теории относительности и др.

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ - раздел геометрии, в котором свойства кривых, поверхностей и других геометрических многообразий изучаются методами математического анализа, в первую очередь - дифференциального исчисления. Работы по дифференциальной геометрии К. Гаусса (1777-1855), Г. Дарбу (1842-1917), Л. Бианки (1856-1928) и Л. Эйзенхарта (1876-1965) посвящены, главным образом, свойствам, проявляющимся в малой окрестности обычной точки многообразия. Это предмет так называемой дифференциальной геометрии "в малом". Более поздние работы, особенно начиная с 1930-х годов, посвящены изучению взаимосвязей между дифференциальной геометрией малых окрестностей и "глобальными" свойствами всего многообразия. Эту теорию называют дифференциальной геометрией "в целом". Кроме того, дифференциальная геометрия разбивается на разделы по аналогии с подразделением всей геометрии. Если на рассматриваемом многообразии определено расстояние, то возникает "метрическая" дифференциальная геометрия, называемая римановой в честь ее создателя Б. Римана (1826-1866). Аналогично проективная, аффинная и конформная дифференциальные геометрии занимаются изучением дифференциальных свойств пространств, в которых выделяются проективные, аффинные или конформные аспекты. Хотя первоначально дифференциальная геометрия занималась изучением свойств кривых и поверхностей в обычном пространстве, ныне она изучает многообразия любого числа измерений, которые могут быть (а могут и не быть) подпространствами евклидова пространства.

Кривые на плоскости и в пространстве. Будем задавать кривые на плоскости параметрическими уравнениями x = f (s), y = g (s), где s - натуральный параметр, длина дуги кривой. В векторной форме это можно записать так: X = F(s).

См. также ВЕКТОР. Тогда единичный вектор касательной к кривой задается формулой

Вектор dT/ds в каждой точке кривой перпендикулярен к касательной, а его длина равна кривизне k кривой. Прямая, перпендикулярная касательной, проходящая через точку касания, называется нормалью к кривой. Следовательно, если N - единичный вектор нормали, то

Кроме того, можно показать, что

Если k задана как функция от s, например, k = f(s), то уравнения (1)-(3) определяют кривую однозначно с точностью до ее положения на плоскости. Соотношение k = f(s) называется внутренним уравнением кривой. Кривая в обычном пространстве, не лежащая на плоскости, называется пространственной кривой. Чтобы исследовать дифференциальную геометрию такой кривой, зададим ее параметрическими уравнениями x = f(s), y = g(s), z = k(s) (s - натуральный параметр) или, в векторной форме, уравнением X = F(s). Единичный вектор касательной определяется равенством

Вектор dT/ds в каждой точке задает нормаль к кривой; заметим, что это лишь одна из бесконечного множества нормалей к пространственной кривой в этой точке. Единичный вектор в направлении вектора dT/ds называется единичным вектором главной нормали N кривой, а длина вектора dT/ds, как и в случае плоских кривых, называется кривизной кривой:

Вектор dN/ds перпендикулярен к N, и поэтому его можно записать в виде

где B - единичный вектор нормали, перпендикулярной к N. Прямая, определяемая вектором B, называется бинормалью к кривой, а коэффициент t в (6) - кручением кривой. Наконец, рассмотрим вектор dB/ds; можно показать, что

Соотношения (5)-(7) называются формулами Френе. Из них следует, что если функции k = f (s) и t = y (s) заданы, то кривая определена однозначно с точностью до положения в пространстве. Таким образом, в этих формулах содержится вся теория пространственных кривых. Плоскость, определяемая векторами T и N, называется соприкасающейся, плоскость, содержащая векторы N и B, - нормальной и плоскость, проходящая через векторы B и T, - спрямляющей.

Поверхности в пространстве. Дифференциальные свойства поверхностей в обычном пространстве выводятся из их первой и второй основных квадратичных форм. Пусть поверхность задана параметрическими уравнениями x = f (u1, u2), y = g (u1, u2), z = h (u1, u2) или векторным уравнением X = F (u1, u2). (Верхними индексами здесь нумеруются переменные.) Дифференциал длины дуги ds определяется первой основной формой, а именно

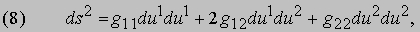
где g11, g12 и g22 - функции от u1 и u2, определяемые выражениями

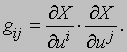
Полезно также ввести величины gij:

Первая фундаментальная форма полностью определяет внутреннюю геометрию поверхности, т.е. ту геометрию, которую наблюдал бы воображаемый обитатель поверхности, неспособный воспринимать происходящие вне нее явления. Такое двумерное существо находилось бы в положении, сравнимом с положением обычного трехмерного человека, воспринимающего геометрию нашего трехмерного пространства, но неспособного воспринимать свойства пространства большего числа измерений, в котором лежит наше пространство (если такое пространство действительно существует). Плоскость, касательная к поверхности в точке P, определяется двумя векторами в P, задаваемыми формулами

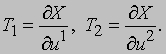
Единичный вектор нормали N определяется как общий перпендикуляр к T1 и T2. Как и в теории кривых, удобно рассмотреть векторы ¶Ti/¶uj (i, j = 1, 2). Эти векторы можно разложить по направлениям векторов T1, T2 и N :

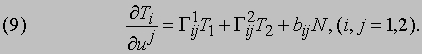
Величины Гijk в (9) называются символами Кристоффеля второго рода. Они определяются через величины [[i, j, k]] (символы Кристоффеля первого рода) соотношениями

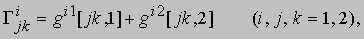
где по определению

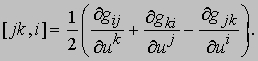
Величины bij в (9) называются коэффициентами второй основной формы поверхности. Сравнивая (9) с (5), нетрудно видеть, что для поверхности bij играют такую же роль, как кривизна для плоских кривых: они описывают внешние свойства поверхности - непостижимые для воображаемого двумерного существа, живущего на поверхности, но доступные пониманию обычного трехмерного человека. Любой единичный вектор, касательный к поверхности, может быть записан в виде

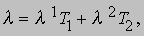
где g11l1l1 + 2g12l1l2 + g22l2l2 = 1. Кривизна поверхности в направлении вектора l равна

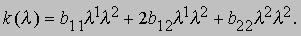
За полуоборот вектора l кривизна k(l) изменяется и достигает в общем случае ровно одного максимального и одного минимального значения. Эти значения соответствуют двум положениям вектора l, находящимся под прямым углом друг к другу, а соответствующие значения k(l) называются главными кривизнами поверхности. Произведение главных кривизн называется полной (гауссовой) кривизной K поверхности, а их сумма - средней кривизной H. Эти величины определяются выражениями

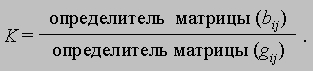
и

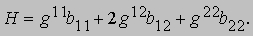
Важную роль играют поверхности с постоянной гауссовой кривизной. При K = 0 поверхность плоская, или развертывающаяся, поскольку у нее такая же внутренняя геометрия, как у плоскости. Примерами развертывающихся поверхностей могут служить прямые круговые конусы и цилиндры. При K > 0 поверхность имеет эллиптическую неевклидову геометрию, а при K < 0 - гиперболическую неевклидову геометрию. Гаусс доказал замечательную теорему относительно кривизны K, утверждающую, что она может быть выражена через одни лишь внутренние величины, а именно через gij и их производные. Это следует из того, что определитель матрицы (bij) равен R1212, где

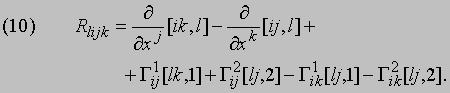
Величина (Rlijk) называется тензором кривизны поверхности.

Риманова геометрия. Обобщением и абстрактным вариантом только что описанной геометрии поверхности служит риманова геометрия. Она описывает n-мерное многообразие, на котором элемент длины дуги определяется формулой

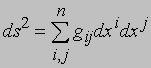
в некоторой системе координат по аналогии с (8). На обычной поверхности определитель матрицы (gij) положителен, в римановой же геометрии предполагается лишь, что он отличен от нуля. Риманово пространство с римановой геометрией необязательно является подпространством пространства какой-нибудь более высокой размерности. Символы Кристоффеля и тензор кривизны определяются через gij, как и в описанном выше случае обычных поверхностей. Секционная кривизна K12 риманова пространства в точке P определяется через ориентацию, задаваемую двумя векторами l1 и l2:

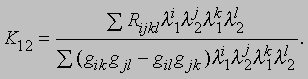
Если она одинакова для всех векторов l1 и l2, то она постоянна и для всех точек P, и пространство называется пространством постоянной кривизны, скажем K, где

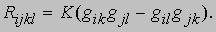
Свернутый тензор кривизны, определяемый выражением

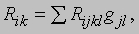
играет важную роль в общей теории относительности Эйнштейна. Пространство, в котором Rik = mgij, называется пространством Эйнштейна. Дифференциальная геометрия в целом. Наиболее фундаментальная из известных взаимосвязей между топологией и дифференциальной геометрией устанавливается теоремой Гаусса - Бонне, которая утверждает, что для обычных замкнутых поверхностей

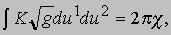
где интеграл берется по всей поверхности, K - гауссова кривизна и c - характеристика Эйлера - Пуанкаре. На произвольные замкнутые римановы пространства этот результат был распространен в 1943 К. Аллендерфером и А. Вейлем.

См. также

МАТЕМАТИЧЕСКИЙ АНАЛИЗ;

ТОПОЛОГИЯ.

ЛИТЕРАТУРА

Рашевский П.К. Курс дифференциальной геометрии. М., 1956 Погорелов А.В. Дифференциальная геометрия. М., 1969 Стернберг С. Лекции по дифференциальной геометрии. М., 1970

Составить слова из слова дифференциальная геометрия

Дифференциа́льная психоло́гия - отрасль психологии, изучающая индивидуальные различия между людьми. Основана Ф. Гальтоном (вторая половина XIX в.), термин введён В. Штерном (1900). Крупные представители: А. Бине, А. Ф. Лазурский, Дж. Кеттел (J. Cattell). В дифференциальной психологии применяются тесты и методы факторного анализа. Выводы важны для решения многих практических задач (отбор и обучение персонала, диагностика и прогностика развития способностей индивидов и др.).

* * *

ДИФФЕРЕНЦИАЛЬНАЯ ПСИХОЛОГИЯ - ДИФФЕРЕНЦИ́АЛЬНАЯ ПСИХОЛО́ГИЯ, отрасль психологии, изучающая индивидуальные различия между людьми. Основана Ф. Гальтоном (см. ГАЛЬТОН Фрэнсис) (2-я пол. 19 в.), термин введен В. Штерном (1900), крупные представители: А. Бине, А. Ф. Лазурский, Дж. Кеттел (J. Cattell). В дифференциальной психологии применяются тесты и методы факторного анализа. Выводы важны для решения многих практических задач (отбор и обучение персонала, диагностика и прогностика развития способностей индивидов и др.).

ДИФФЕРЕНЦИАЛЬНАЯ ПСИХОЛОГИЯ - отрасль психологии, изучающая индивидуальные различия между людьми. Основана Ф. Гальтоном (2-я пол. 19 в.), термин введен В. Штерном (1900), крупные представители: А. Бине, А. Ф. Лазурский, Дж. Кеттел (J. Cattell). В дифференциальной психологии применяются тесты и методы факторного анализа. Выводы важны для решения многих практических задач (отбор и обучение персонала, диагностика и прогностика развития способностей индивидов и др.).

ДИФФЕРЕНЦИА́ЛЬНАЯ ПСИХОЛО́ГИЯ (англ. differencial psychology).

Раздел психологии, изучающий индивидуально-психологические различия между людьми. Термин Д. п. введен немецким психологом В. Штерном (1900). Д. п. изучает как психологические различия конкретных людей, так и типологические различия психологических проявлений у представителей разных социальных, этнических, возрастных и др. групп. Для исследования особенностей индивида используются метод наблюдения, тесты или анализ результатов самонаблюдения. Для изучающих иностранные языки особенно важными представляются индивидуальные особенности памяти учащихся, способности к овладению языком, а также принадлежность учащегося к коммуникативному или некоммуникативному типу. См. индивидуально-психлогические различия.

Составить слова из слова дифференциальная психология

Дифференциа́льная ре́нта - форма земельной ренты, порождается монополией на землю как объект хозяйства. Представляет собой добавочную прибыль, возникающую как разница в производительности труда при равновеликих затратах на средних и лучших (по местоположению или плодородию) землях (дифференциальная рента I) или при добавочных вложениях капитала на одном и том же земельном участке (дифференциальная рента II). Источник дифференциальной ренты - прибавочная стоимость, создаваемая в сельском хозяйстве.

* * *

ДИФФЕРЕНЦИАЛЬНАЯ РЕНТА - ДИФФЕРЕНЦИА́ЛЬНАЯ РЕ́НТА, форма земельной ренты, порождается монополией на землю как объект хозяйства. Представляет собой добавочную прибыль, возникающую как разница в производительности труда при равновеликих затратах на средних и лучших (по местоположению или плодородию) землях (дифференциальная рента I) или при добавочных вложениях капитала на одном и том же земельном участке (дифференциальная рента II). Источник дифференциальной ренты - прибавочная стоимость, создаваемая в сельском хозяйстве.

ДИФФЕРЕНЦИАЛЬНАЯ рента - форма земельной ренты, порождается монополией на землю как объект хозяйства. Представляет собой добавочную прибыль, возникающую как разница в производительности труда при равновеликих затратах на средних и лучших (по местоположению или плодородию) землях (дифференциальная рента I) или при добавочных вложениях капитала на одном и том же земельном участке (дифференциальная рента II). Источник дифференциальной ренты - прибавочная стоимость, создаваемая в сельском хозяйстве.

Составить слова из слова дифференциальная рента

дифференциа/льно анализи/руемый

Составить слова из слова дифференциально анализируемый

дифференциа/льно рассмо/тренный

Составить слова из слова дифференциально рассмотренный

дифференциа/льно-алгебраи/ческий

Составить слова из слова дифференциально-алгебраический

дифференциа/льно-геометри/ческий

Составить слова из слова дифференциально-геометрический

дифференциа́льно-диагности́ческий

Составить слова из слова дифференциально-диагностический

дифференциа/льно-психологи/ческий

Составить слова из слова дифференциально-психологический

дифференциа́льно-ра́зностный

прил., кол-во синонимов: 1

дифференци/а́льн/о/-ра́зн/ост/н/ый.

Составить слова из слова дифференциально-разностный

дифференциа/льно-функциона/льный

Составить слова из слова дифференциально-функциональный

Дифференциа́льное исчисле́ние - раздел математики, в котором изучаются производные, дифференциалы и их применения к исследованию свойств функций. Производной функции у = f(х) называется предел отношения приращения Δу = у₁ - у₀ функции к приращению Δх = x₁ - х₀ аргумента при Δх, стремящемся к нулю (если этот предел существует).

Производная обозначается f'(х) или у'; т.о., 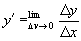. Дифференциалом функции у = f(х) называется выражение dy = у´dx, где dx = Δх - приращение аргумента х. Очевидно, что у' = dy/dx. Отношение dy/dx часто употребляют как знак производной. Вычисление производных и дифференциалов называют дифференцированием. Если производная f'(х) имеет, в свою очередь, производную, то её называют второй производной функции f(x) и обозначают f"(х), и т. д. Основные понятия дифференциального исчисления могут быть распространены на случай функций нескольких переменных. 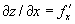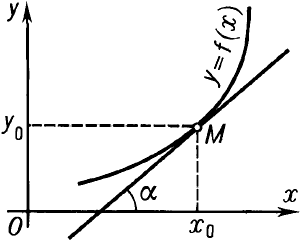Если z = f(х, у) - функция двух переменных х и у, то, зафиксировав для у какое-либо значение, можно дифференцировать z по х; полученная производная называется частной производной z по х. Аналогично определяются частная производная 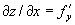, частные производные высших порядков, частные и полные дифференциалы. Для приложений дифференциального исчисления к геометрии важно, что так называемый угловой коэффициент касательной, то есть тангенс угла α (см. рис.) между осью Ох и касательной к кривой у = f(х) в точке М(х₀, у₀), равен значению производной при х = х₀, то есть f'(х₀). В механике скорость прямолинейно движущейся точки можно истолковать как производную пути по времени. Дифференциальное исчисление (как и интегральное исчисление) имеет многочисленные применения.

* * *

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ - ДИФФЕРЕНЦИА́ЛЬНОЕ ИСЧИСЛЕ́НИЕ, раздел математики, в котором изучаются производные, дифференциалы и их применения к исследованию свойств функций.

Производной функции y = f(х) называется предел отношения приращения Dy = y₁ - y₀ функции к приращению Dx = x₁ - x₀ аргумента при Dx, стремящемся к нулю (если этот предел существует). Дифференциалом функции y = f(x) называется выражение dy = yўdx, где dx = Dx - приращение аргумента x. Очевидно, что yў = dy/dx. Отношение dy/dx часто употребляют как знак производной. Вычисление производных и дифференциалов называют дифференцированием. Если производная fў(x) имеет, в свою очередь, производную, то ее называют 2-й производной функции f(x) и обозначают fўў(x), и т. д. Основные понятия дифференциального исчисления могут быть распространены на случай функций нескольких переменных. Если z = f(x,y) - функция двух переменных x и y, то, зафиксировав для y какое-либо значение, можно дифференцировать z по x; полученная производная dz/dx = fў_x называется частной производной z по x. Аналогично определяются частная производная dz/dy = fў_y, частные производные высших порядков, частные и полные дифференциалы.

Для приложений дифференциального исчисления к геометрии важно, что т. н. угловой коэффициент касательной, т. е. тангенс угла a между осью Ox и касательной к кривой y = f(x) в точке M(x₀, y₀), равен значению производной при x = x₀, т. е. fў(x₀). В механике скорость прямолинейно движущейся точки можно истолковать как производную пути по времени. Дифференциальное исчисление (как и интегральное исчисление (см. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ)) имеет многочисленные применения.

ДИФФЕРЕНЦИАЛЬНОЕ исчисление - раздел математики, в котором изучаются производные, дифференциалы и их применения к исследованию свойств функций. Производной функции y = f(х) называется предел отношения приращения ?y = y1 - y0 функции к приращению ?x = x1 - x0 аргумента при ?x, стремящемся к нулю (если этот предел существует). производная обозначается f?(x) или y?; таким образом, Дифференциалом функции y = f(x) называется выражение dy = y?dx, где dx = ?x - приращение аргумента x. Очевидно, что y? = dy/dx. Отношение dy/dx часто употребляют как знак производной.

Вычисление производных и дифференциалов называют дифференцированием. Если производная f?(x) имеет, в свою очередь, производную, то ее называют 2-й производной функции f(x) и обозначают f??(x), и т. д. Основные понятия дифференциального исчисления могут быть распространены на случай функций нескольких переменных. Если z = f(x,y) - функция двух переменных x и y, то, зафиксировав для y какое-либо значение, можно дифференцировать z по x; полученная производная dz/dx = f?x называется частной производной z по x. Аналогично определяются частная производная dz/dy = f?y, частные производные высших порядков, частные и полные дифференциалы. Для приложений дифференциального исчисления к геометрии важно, что т. н. угловой коэффициент касательной, т. е. тангенс угла ? (см. рис.) между осью Ox и касательной к кривой y = f(x) в точке M(x0, y0), равен значению производной при x = x0, т. е. f?(x0). В механике скорость прямолинейно движущейся точки можно истолковать как производную пути по времени. Дифференциальное исчисление (как и интегральное исчисление) имеет многочисленные применения.

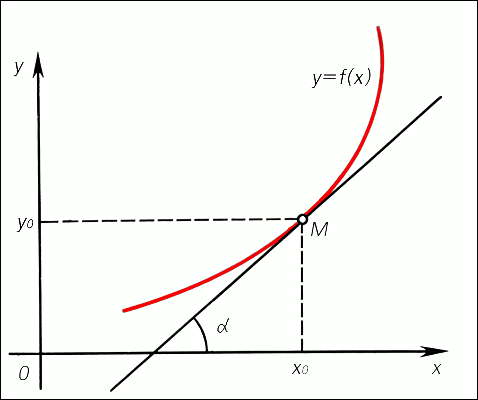
Дифференциальное исчисление. Проведение касательной к графику функции y=f(x) в точке M.

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ, раздел математики, в котором изучаются производные, дифференциалы и их применения к исследованию свойств функций. Производной функции y=f(x) называется предел отношения приращения функции Dy=y₁-y₀ к приращению аргумента Dx=x₁-x₀ при Dx, стремящемся к нулю (если этот предел существует). Производная обозначается y'' т.о. y'=lim Dy/Dx при Dx®0. Дифференциалом функции y=f(x) называется выражение dy=y', где dx=y'Dx - приращение аргумента x. Очевидно, что y'=dy/dx. Отношение dy/dx часто употребляют как знак производной. Вычисление производных и дифференциалов называется дифференцированием. Если производная f' (x) имеет, в свою очередь, производную, то ее называют 2-й производной функции f (x) и обозначают f" (x), и т.д. Основные понятия дифференциального исчисления могут быть распространены на случай функций нескольких переменных. Для приложений дифференциального исчисления к геометрии важно, что так называемый угловой коэффициент касательной, т.е. тангенс угла a между осью Ox и касательной к кривой y=f(x) в точке M(x₀, y₀), равен значению производной при x=x₀, т.е. f' (x₀). С точки зрения механики производную от пути по времени можно истолковать как скорость прямолинейно движущейся точки. Дифференциальное исчисление (как и интегральное исчисление) имеет многочисленные применения.

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ - математическая наука, занимающаяся изучением дифференциалов функций, т. е. выражений, показывающих, в какой зависимости переменные величины находятся друг от друга. Дифференциалом функции назыв. бесконечно малое приращение, получаемое ею, соответственно бесконечно малому приращению переменной величины.

Составить слова из слова дифференциальное исчисление

ДИФФЕРЕНЦИАЛЬНОЕ СЧИСЛЕНИЕ (этим. см. предыд. сл.). Часть высшего анализа, имеющая своим предметом дифференциалы (см. это сл.).

Составить слова из слова дифференциальное счисление

Дифференциа́льное уравне́ние - уравнение, связывающее искомую функцию, её производные (или дифференциалы) и независимые переменные, например dy = 2xdx. Решением или интегралом дифференциального уравнения называется функция, при подстановке которой в дифференциальном уравнении последнее обращается в тождество; в приведённом примере решением является всякая функция вида у = х² + С, где С - любая постоянная. Процесс решения дифференциального уравнения называется его интегрированием. При помощи дифференциального уравнения записываются многие реальные процессы, поэтому дифференциальные уравнения имеют исключительно важное значение для естествознания и техники.

* * *

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ - ДИФФЕРЕНЦИА́ЛЬНОЕ УРАВНЕ́НИЕ, уравнение, связывающее искомую функцию, ее производные (или дифференциалы) и независимые переменные, напр. dy = 2xdx. Решением или интегралом дифференциального уравнения называется функция, при подстановке которой в дифференциальное уравнение последнее обращается в тождество; в приведенном примере решением является всякая функция вида y = x² + C, где С - любая постоянная. Процесс решения дифференциального уравнения называется его интегрированием. При помощи дифференциального уравнения записываются многие реальные процессы, поэтому дифференциальные уравнения имеют исключительно важное значение для естествознания и техники.

ДИФФЕРЕНЦИАЛЬНОЕ уравнение - уравнение, связывающее искомую функцию, ее производные (или дифференциалы) и независимые переменные, напр. dy = 2xdx. Решением или интегралом дифференциального уравнения называется функция, при подстановке которой в дифференциальное уравнение последнее обращается в тождество; в приведенном примере решением является всякая функция вида y = x2 + C, где С - любая постоянная. Процесс решения дифференциального уравнения называется его интегрированием. При помощи дифференциального уравнения записываются многие реальные процессы, поэтому дифференциальные уравнения имеют исключительно важное значение для естествознания и техники.

Составить слова из слова дифференциальное уравнение

решать дифференциальные уравнения => решение

Составить слова из слова дифференциальные

дифференциальные признаки - дистинктивные, различительные признаки.

Составить слова из слова дифференциальные признаки

1) закрытость структуры;

2) разнотипность частей в семантическом плане;

3) возможность различного грамматического оформления предикативных частей;

4) использование различных типов интонационного оформления конструкций.

1) закрытость структуры;

2) разнотипность частей в семантическом плане;

3) возможность различного грамматического оформления предикативных частей;

4) использование различных типов интонационного оформления конструкций.

Составить слова из слова дифференциальные признаки бессоюзных сложных предложений неоднородного состава

1) характер соотношения чужой и авторской речи:

а) с точки зрения героя и автора совмещаются;

б) типична буквальная передача содержания чужой речи;

2) лингвистические признаки способов передачи несобственно-прямой речи:

а) позволяет сохранить все особенности передаваемой речи;

б) наличие вводящих слов автора типично, но не обязательно;

в) интонация независимая;

г) грамматические признаки: связь частей конструкции бессоюзная; формы лица употребляются с точки зрения автора (зависимое употребление);

д) кавычками и тире не выделяется (в остальных случаях пунктуационное оформление, как у прямой речи).

1) характер соотношения чужой и авторской речи: а) с точки зрения героя и автора совмещаются; б) типична буквальная передача содержания чужой речи;

2) лингвистические признаки способов передачи несобствен-нопрямой речи: а) позволяет сохранить все особенности передаваемой речи; б) наличие вводящих слов автора типично, но не обязательно; в) интонация независимая; г) грамматические признаки: связь частей конструкции бессоюзная; формы лица употребляются с точки зрения автора (зависимое употребление); д) кавычками и тире не выделяется (в остальных случаях пунктуационное оформление, как у прямой речи).

Составить слова из слова дифференциальные признаки несобственно-прямой речи

1) основной способ действия механизмов связи - повтор;

2) ведущие средства связи: лексические повторы, слова одной тематической или лексико-семантической группы;

3) последовательность с константной темой или с производными темами.

1) основной способ действия механизмов связи - повтор;

2) ведущие средства связи: лексические повторы, слова одной тематической или лексико-семантической группы;

3) последовательность с константной темой или с производными темами.

Составить слова из слова дифференциальные признаки параллельной связи

1) характер соотношения чужой и авторской речи:

а) чужая речь передается с точки зрения говорящего (героя);

б) типична буквальная передача содержания чужой речи;

2) лингвистические признаки прямой речи:

а) позволяет сохранить все лексико-фразеологические и синтаксические особенности передаваемой речи;

б) наличие слов автора типично, но их может не быть;

в) интонация независимая;

г) грамматические признаки: связь прямой речи и слов автора бессоюзная; употребление форм лица независимое;

д) прямая речь выделяется кавычками или тире с абзаца.

1) характер соотношения чужой и авторской речи: а) чужая речь передается с точки зрения говорящего (героя); б) типична буквальная передача содержания чужой речи;

2) лингвистические признаки прямой речи: а) позволяет сохранить все лексико-фразеологические и синтаксические особенности передаваемой речи; б) наличие слов автора типично, но их может не быть; в) интонация независимая; г) грамматические признаки: связь прямой речи и слов автора бессоюзная; употребление форм лица независимое; д) прямая речь выделяется кавычками или тире с абзаца.

Составить слова из слова дифференциальные признаки прямой речи

1) зависимость придаточной предикативной части от главной;

2) наличие подчинительного союза или союзного слова, вводящего придаточную часть в СПП;

3) ступенчатость (многоярусность) коммуникативной структуры.

1) зависимость придаточной предикативной части от главной;

2) наличие подчинительного союза или союзного слова, вводящего придаточную часть в СПП;

3) ступенчатость (многоярусность) коммуникативной структуры.

Составить слова из слова дифференциальные признаки сложноподчиненного предложения

дифференциальные признаки сложноподчиненных предложений с неоднородным (параллельным) соподчинением:

1) придаточные части относятся к разным словам в главной части (разночленное соподчинение) или являются присловными, присоставными;

2) между придаточными частями не возникает сочинительной связи;

3) разнофункциональность и разнотипность придаточных определяют различие средств связи.

Составить слова из слова дифференциальные признаки сложноподчиненных предложений с неоднородным

1) придаточные части относятся к разным словам в главной части (разночленное соподчинение) или являются присловными, присоставными;

2) между придаточными частями не возникает сочинительной связи;

3) разнофункциональность и разнотипность придаточных определяют различие средств связи.

Составить слова из слова дифференциальные признаки сложноподчиненных предложений с неоднородным (параллельным) соподчинением

1) придаточные части распространяют одно слово главной части или весь ее состав;

2) придаточные части могут быть связаны сочинительной связью;

3) придаточные части присоединяются к главной части одинаковыми союзами или союзными словами.

1) придаточные части распространяют одно слово главной части или весь ее состав;

2) придаточные части могут быть связаны сочинительной связью;

3) придаточные части присоединяются к главной части одинаковыми союзами или союзными словами.

Составить слова из слова дифференциальные признаки сложноподчиненных предложений с однородным соподчинением

1) закрытость структуры: количество предикативных частей не может быть увеличено;

2) неравноправие предикативных частей в смысловом отношении;

3) более широкий круг союзных средств связи и употребление союзов, подчеркивающих неравноправие частей;

4) различная оформленность предикативных частей;

5) использование различных интонационных типов: разделительной, противительной, пояснительной интонации, интонации, характерной для присоединения.

Формальные показатели неоднородности состава ССП:

1) невозможность общего члена, одновременно относящегося к двум предикативным частям;

2) наличие во второй предикативной части анафорических местоимений и местоименных наречий - показателей синсемантичности (неполноценности) той части, в которой они находятся;

3) употребление во второй предикативной части наречий и частиц со значением следствия, уступки, ограничения, возмещения - конкретизаторов частного синтаксического значения, подчеркивающих неравноправие одной из частей сложносочиненного предложения.

1) закрытость структуры: количество предикативных частей не может быть увеличено;

2) неравноправие предикативных частей в смысловом отношении;

3) более широкий круг союзных средств связи и употребление союзов, подчеркивающих неравноправие частей;

4) различная оформленность предикативных частей;

5) использование различных интонационных типов: разделительной, противительной, пояснительной интонации, интонации, характерной для присоединения.

Формальные показатели неоднородности состава ССП:

1) невозможность общего члена, одновременно относящегося к двум предикативным частям;

2) наличие во второй предикативной части анафорических местоимений и местоименных наречий - показателей синсемантичности (неполноценности) той части, в которой они находятся;

3) употребление во второй предикативной части наречий и частиц со значением следствия, уступки, ограничения, возмещения - конкретизаторов частного синтаксического значения, подчеркивающих неравноправие одной из частей сложносочиненного предложения.

Составить слова из слова дифференциальные признаки сложносочиненных предложений неоднородного состава

1) открытость структуры: ряд, состоящий из двух частей, может быть продолжен до трех и более;

2) смысловое и граматическое равноправие частей;

3) использование в качестве основных средств связи соединительных, разделительных союзов, противительного союза а (в редких случаях);

4) одинаковая оформленность каждой предикативной части: общий модальный план, единство функциональных типов;

5) перечислительная интонация, характеризующаяся однообразием ритмико-мелодического рисунка

Об однородности состава ССП свидетельствуют следующие показатели

1) наличие или возможность общего второстепенного члена или общей предикативной части;

2) наличие общего для обеих предикативных частей предложения в предшествующем или последующем контексте, с которым они одинаково соотносятся;

3) наличие общей оценки или общей картины, определяющей тематическое сходство частей или их ассоциативное сближение.

1) открытость структуры: ряд, состоящий из двух частей, может быть продолжен до трех и более;

2) смысловое и граматическое равноправие частей;

3) использование в качестве основных средств связи соединительных, разделительных союзов, противительного союза а (в редких случаях);

4) одинаковая оформленность каждой предикативной части: общий модальный план, единство функциональных типов;

5) перечислительная интонация, характеризующаяся однообразием ритмикомелодического рисунка.

Об однородности состава ССП свидетельствуют следующие показатели:

1) наличие или возможность общего второстепенного члена или общей предикативной части;

2) наличие общего для обеих предикативных частей предложения в предшествующем или последующем контексте, с которым они одинаково соотносятся;

3) наличие общей оценки или общей картины, определяющей тематическое сходство частей или их ассоциативное сближение.

Составить слова из слова дифференциальные признаки сложносочиненных предложений однородного состава

1) характер соотношения чужой и авторской речи:

а) чужая речь передается с точки зрения автора;

б) типична передача основного содержания чужой речи;

2) лингвистические признаки чужой речи:

а) не позволяет сохранить всех особенностей передаваемой речи;

б) наличие вводящих слов автора обязательно;

в) интонация предложений косвенной речи зависимая;

г) грамматические признаки: связь с помощью союзов или союзных слов, т.к. косвенная речь передается придаточным предложением; формы лица употребляются с точки зрения автора (зависимое употребление);

д) косвенная речь кавычками не выделяется.

1) характер соотношения чужой и авторской речи: а) чужая речь передается с точки зрения автора; б) типична передача основного содержания чужой речи;

2) лингвистические признаки чужой речи: а) не позволяет сохранить всех особенностей передаваемой речи; б) наличие вводящих слов автора обязательно; в) интонация предложений косвенной речи зависимая; г) грамматические признаки: связь с помощью союзов или союзных слов, т.к. косвенная речь передается придаточным предложением; формы лица употребляются с точки зрения автора (зависимое употребление); д) косвенная речь кавычками не выделяется.

Составить слова из слова дифференциальные признаки способов передачи косвенной речи

дифференциальные признаки фонем (от лат. differens - различающий). Признаки, которыми данная фонема противопоставляется другим фонемам языка, ее смыслоразличительные признаки (например, вокальность - невокальность, консонатность - неконсонантность; глухость - звонкость, взрывность -фрикативность, огубление - неогубление и т. д.).

Составить слова из слова дифференциальные признаки фонем

1) основной способ действия механизмов связи - зацепление;

2) средства связи:

а) анафорические замены (местоименные слова);

б) синсемантические элементы (союзы, наречия, слова широкой семантики, отсылающие к предшествующим предложениям);

3) простая линейная тематическая последовательность, когда рема предшествующего предложения становится темой последующего, или комбинации, основанные на такой последовательности.

1) основной способ действия механизмов связи - зацепление;

2) средства связи: а) анафорические замены (местоименные слова); б) синсемантические элементы (союзы, наречия, слова широкой семантики, отсылающие к предшествующим предложениям);

3) простая линейная тематическая последовательность, когда рема предшествующего предложения становится темой последующего, или комбинации, основанные на такой последовательности.

Составить слова из слова дифференциальные признаки цепной связи

1) семы содержательного характера;

2) семы, характеризующие стилевую принадлежность синонима;

3) стилистические коннотативные семы.

1) семы содержательного характера;

2) семы, характеризующие стилевую принадлежность синонима;

3) стилистические коннотативные семы.

Составить слова из слова дифференциальные семы в синонимической парадигме

Многие физические законы, которым подчиняются те или иные явления, записываются в виде математического уравнения, выражающего определенную зависимость между какими-то величинами. Часто речь идет о соотношении между величинами, изменяющимися с течением времени, например экономичность двигателя, измеряемая расстоянием, которое автомашина может проехать на одном литре горючего, зависит от скорости движения автомашины. Соответствующее уравнение содержит одну или несколько функций и их производных и называется дифференциальным уравнением. (Темп изменения расстояния со временем определяется скоростью; следовательно, скорость - производная от расстояния; аналогично, ускорение - производная от скорости, так как ускорение задает темп изменения скорости со временем.) Большое значение, которое имеют дифференциальные уравнения для математики и особенно для ее приложений, объясняются тем, что к решению таких уравнений сводится исследование многих физических и технических задач. Дифференциальные уравнения играют существенную роль и в других науках, таких, как биология, экономика и электротехника; в действительности, они возникают везде, где есть необходимость количественного (числового) описания явлений (коль скоро окружающий мир изменяется во времени, а условия изменяются от одного места к другому).

См. также МАТЕМАТИЧЕСКИЙ АНАЛИЗ.

Примеры. Следующие примеры позволяют лучше понять, как различные задачи формулируются на языке дифференциальных уравнений. 1) Закон распада некоторых радиоактивных веществ состоит в том, что скорость распада пропорциональна наличному количеству этого вещества. Если x - количество вещества в некоторый момент времени t, то этот закон можно записать так:

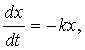
где dx/dt - скорость распада, а k - некоторая положительная постоянная, характеризующая данное вещество. (Знак "минус" в правой части указывает на то, что x убывает со временем; знак "плюс", подразумеваемый всегда, когда знак явно не указан, означал бы, что x возрастает со временем.) 2) Емкость первоначально содержит 10 кг соли, растворенной в 100 м3 воды. Если чистая вода вливается в емкость со скоростью 1 м3 в минуту и равномерно перемешивается с раствором, а образовавшийся раствор вытекает из емкости с такой же скоростью, то сколько соли окажется в емкости в любой последующий момент времени? Если x - количество соли (в кг) в емкости в момент времени t, то в любой момент времени t в 1 м3 раствора в емкости содержится x/100 кг соли; поэтому количество соли убывает со скоростью x/100 кг/мин, или

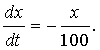
3) Пусть на тело массы m, подвешенное к концу пружины, действует возвращающая сила, пропорциональная величине растяжения пружины. Пусть x - величина отклонения тела от положения равновесия. Тогда по второму закону Ньютона, который утверждает, что ускорение (вторая производная от x по времени, обозначаемая d 2x/dt 2) пропорционально силе:

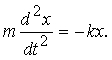
Правая часть стоит со знаком минус потому, что возвращающая сила уменьшает растяжение пружины. 4) Закон охлаждения тел утверждает, что количество тепла в теле убывает пропорционально разности температур тела и окружающей среды. Если чашка кофе, разогретого до температуры 90° С находится в помещении, температура в котором равна 20° С, то

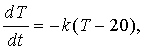
где T - температура кофе в момент времени t. 5) Министр иностранных дел государства Блефуску утверждает, что принятая Лиллипутией программа вооружений вынуждает его страну увеличить военные расходы на сколько это только возможно. С аналогичными заявлениями выступает и министр иностранных дел Лиллипутии. Возникающую в результате ситуацию (в простейшей интерпретации) можно точно описать двумя дифференциальными уравнениями. Пусть x и y - расходы на вооружение Лиллипутии и Блефуску. Предполагая, что Лиллипутия увеличивает свои расходы на вооружение со скоростью, пропорциональной скорости увеличения расходов на вооружение Блефуску, и наоборот, получаем:

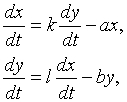
где члены -ax и -by описывают военные расходы каждой из стран, k и l - положительные постоянные. (Эту задачу впервые таким образом сформулировал в 1939 Л.Ричардсон.) После того, как задача записана на языке дифференциальных уравнений, следует попытаться их решить, т.е. найти величины, скорости изменения которых входят в уравнения. Иногда решения находятся в виде явных формул, но чаще их удается представить лишь в приближенном виде или же получить о них качественную информацию. Часто бывает трудно установить, существует ли решение вообще, не говоря уже о том, чтобы найти его. Важный раздел теории дифференциальных уравнений составляют так называемые "теоремы существования", в которых доказывается наличие решения у того или иного типа дифференциальных уравнений. Первоначальная математическая формулировка физической задачи обычно содержит упрощающие предположения; критерием их разумности может служить степень согласованности математического решения с имеющимися наблюдениями.

Решения дифференциальных уравнений. Дифференциальному уравнению, например dy/dx = x/y, удовлетворяет не число, а функция, в данном конкретном случае такая, что ее график в любой точке, например в точке с координатами (2,3), имеет касательную с угловым коэффициентом, равным отношению координат (в нашем примере 2/3). В этом нетрудно убедиться, если построить большое число точек и от каждой отложить короткий отрезок с соответствующим наклоном. Решением будет функция, график которой касается каждой своей точкой соответствующего отрезка. Если точек и отрезков достаточно много, то мы можем приближенно наметить ход кривых-решений (три такие кривые показаны на рис. 1). Существует ровно одна кривая-решение, проходящая через каждую точку с y № 0. Каждое отдельное решение называется частным решением дифференциального уравнения; если удается найти формулу, содержащую все частные решения (за исключением, быть может, нескольких особых), то говорят, что получено общее решение. Частное решение представляет собой одну функцию, в то время как общее - целое их семейство. Решить дифференциальное уравнение - это значит найти либо его частное, либо общее решение. В рассматриваемом нами примере общее решение имеет вид y2 - x2 = c, где c - любое число; частное решение, проходящее через точку (1,1), имеет вид y = x и получается при c = 0; частное решение, проходящее через точку (2,1), имеет вид y2 - x2 = 3. Условие, требующее, чтобы кривая-решение проходила, например, через точку (2,1), называется начальным условием (так как задает начальную точку на кривой-решении).

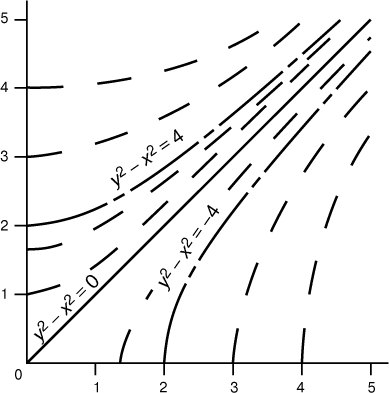
Рис. 1.

Можно показать, что в примере (1) общее решение имеет вид x = ce-kt, где c - постоянная, которую можно определить, например, указав количество вещества при t = 0. Уравнение из примера (2) - частный случай уравнения из примера (1), соответствующий k = 1/100. Начальное условие x = 10 при t = 0 дает частное решение x = 10e-t/100. Уравнение из примера (4) имеет общее решение T = 70 + ce-kt и частное решение 70 + 130-kt; чтобы определить значение k, необходимы дополнительные данные. Дифференциальное уравнение dy/dx = x/y называется уравнением первого порядка, так как содержит первую производную (порядком дифференциального уравнения принято считать порядок входящей в него самой старшей производной). У большинства (хотя и не у всех) возникающих на практике дифференциальных уравнений первого рода через каждую точку проходит только одна кривая-решение. Существует несколько важных типов дифференциальных уравнений первого порядка, допускающих решения в виде формул, содержащих только элементарные функции - степени, экспоненты, логарифмы, синусы и косинусы и т.д. К числу таких уравнений относятся следующие. Уравнения с разделяющимися переменными. Уравнения вида dy/dx = f(x)/g(y) можно решить, записав его в дифференциалах g(y)dy = f(x)dx и проинтегрировав обе части. В худшем случае решение представимо в виде интегралов от известных функций. Например, в случае уравнения dy/dx = x/y имеем f(x) = x, g(y) = y. Записав его в виде ydy = xdx и проинтегрировав, получим y2 = x2 + c. К уравнениям с разделяющимися переменными относятся уравнения из примеров (1), (2), (4) (их можно решить описанным выше способом).

Уравнения в полных дифференциалах. Если дифференциальное уравнение имеет вид dy/dx = M(x,y)/N(x,y), где M и N - две заданные функции, то его можно представить как M(x,y)dx - N(x,y)dy = 0. Если левая часть является дифференциалом некоторой функции F(x,y), то дифференциальное уравнение можно записать в виде dF(x,y) = 0, что эквивалентно уравнению F(x,y) = const. Таким образом, кривые-решения уравнения - это "линии постоянных уровней" функции, или геометрические места точек, удовлетворяющих уравнениям F(x,y) = c. Уравнение ydy = xdx (рис. 1) - с разделяющимися переменными, и оно же - в полных дифференциалах: чтобы убедиться в последнем, запишем его в виде ydy - xdx = 0, т.е. d(y2 - x2) = 0. Функция F(x,y) в этом случае равна (1/2)(y2 - x2); некоторые из ее линий постоянного уровня представлены на рис. 1.

Линейные уравнения. Линейные уравнения - это уравнения "первой степени" - неизвестная функция и ее производные входят в такие уравнения только в первой степени. Таким образом, линейное дифференциальное уравнение первого порядка имеет вид dy/dx + p(x) = q(x), где p(x) и q(x) - функции, зависящие только от x. Его решение всегда можно записать с помощью интегралов от известных функций. Многие другие типы дифференциальных уравнений первого порядка решаются с помощью специальных приемов.

Уравнения старших порядков. Многие дифференциальные уравнения, с которыми сталкиваются физики, это уравнения второго порядка (т.е. уравнения, содержащие вторые производные) Таково, например, уравнение простого гармонического движения из примера (3), md 2x/dt 2 = -kx. Вообще говоря, можно ожидать, что уравнение второго порядка имеет частные решения, удовлетворяющие двум условиям; например, можно потребовать, чтобы кривая-решение проходила через данную точку в данном направлении. В случаях, когда дифференциальное уравнение содержит некоторый параметр (число, величина которого зависит от обстоятельств), решения требуемого типа существуют только при определенных значениях этого параметра. Например, рассмотрим уравнение md 2x/dt 2 = -kx и потребуем, чтобы y(0) = y(1) = 0. Функция y є 0 заведомо является решением, но если - целое кратное числа p, т.е. k = m2n2p2, где n - целое число, а в действительности только в этом случае, существуют другие решения, а именно: y = sin npx. Значения параметра, при которых уравнение имеет особые решения, называются характеристическими или собственными значениями; они играют важную роль во многих задачах. Уравнение простого гармонического движения служит примером важного класса уравнений, а именно: линейных дифференциальных уравнений с постоянными коэффициентами. Более общий пример (также второго порядка) - уравнение

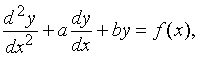
где a и b - заданные постоянные, f(x) - заданная функция. Такие уравнения можно решать различными способами, например, с помощью интегрального преобразования Лапласа. То же можно сказать и о линейных уравнениях более высоких порядков с постоянными коэффициентами. Не малую роль играют также и линейные уравнения с переменными коэффициентами.

Нелинейные дифференциальные уравнения. Уравнения, содержащие неизвестные функции и их производные в степени выше первой или каким-либо более сложным образом, называются нелинейными. В последние годы они привлекают все большее внимание. Дело в том, что физические уравнения обычно линейны лишь в первом приближении; дальнейшее и более точное исследование, как правило, требует использования нелинейных уравнений. Кроме того, многие задачи нелинейны по своей сути. Так как решения нелинейных уравнений зачастую очень сложны и их трудно представить простыми формулами, значительная часть современной теории посвящена качественному анализу их поведения, т.е. разработке методов, позволяющих, не решая уравнения, сказать нечто существенное о характере решений в целом: например, что все они ограниченны, или имеют периодический характер, или определенным образом зависят от коэффициентов. Приближенные решения дифференциальных уравнений могут быть найдены в численном виде, но для этого требуется много времени. С появлением быстродействующих компьютеров это время сильно сократилось, что открыло новые возможности численного решения многих, ранее не поддававшихся такому решению, задач.

Теоремы существования. Теоремой существования называется теорема, утверждающая, что при определенных условиях данное дифференциальное уравнение имеет решение. Встречаются дифференциальные уравнения, не имеющие решений или имеющие их больше, чем ожидается. Назначение теоремы существования - убедить нас в том, что у данного уравнения действительно есть решение, а чаще всего заверить, что оно имеет ровно одно решение требуемого типа. Например, уже встречавшееся нам уравнение dy/dx = -2y имеет ровно одно решение, проходящее через каждую точку плоскости (x,y), а так как одно такое решение мы уже нашли, то тем самым полностью решили это уравнение. С другой стороны, уравнение (dy/dx)2 = 1 - y2 имеет много решений. Среди них прямые y = 1, y = -1 и кривые y = sin(x + c). Решение может состоять из нескольких отрезков этих прямых и кривых, переходящих друг в друга в точках касания (рис. 2).

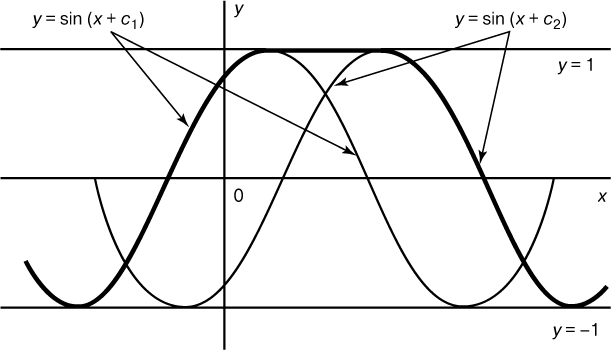
Рис. 2.

Дифференциальные уравнения в частных производных. Обыкновенное дифференциальное уравнение - это некоторое утверждение о производной неизвестной функции одной переменной. Дифференциальное уравнение в частных производных содержит функцию двух или более переменных и производные от этой функции по крайней мере по двум различных переменным. В физике примерами таких уравнений являются уравнение Лапласа

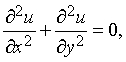
где, согласно одной из возможных интерпретаций, u - температура в плоской области, точки которой задаются координатами x и y; уравнение теплопроводности

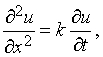
где t - время, x - расстояние от одного из концов однородного стержня, по которому распространяется тепловой поток; и волновое уравнение

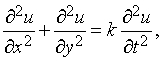
где t - снова время, x и y - координаты точки колеблющейся струны. Решая дифференциальные уравнения в частных производных, обычно не стремятся найти общее решение, поскольку оно скорее всего окажется слишком общим, чтобы быть полезным. Если решение обыкновенного дифференциального уравнения определяется заданием условий в одной или нескольких точках; то решение дифференциального уравнения в частных производных обычно определяется заданием условий на одной или нескольких кривых. Например, решение уравнения Лапласа может быть найдено в точке (x, y) внутри круга, если значения u заданы в каждой точке ограничивающей окружности. Поскольку проблемы с более чем одной переменной в физике являются скорее правилом, чем исключением, легко представить, сколь обширен предмет теории дифференциальных уравнений в частных производных.

ЛИТЕРАТУРА

Тихонов А.Н., Самарский А.А. Уравнения математической физики. М., 1977 Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М., 1982 Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М., 1984 Эрроусмит Д., Плейс К. Обыкновенные дифференциальные уравнения. Качественная теория с приложениями. М., 1986

Составить слова из слова дифференциальные уравнения

I прил.

соотн. с сущ. дифференциал I, связанный с ним

II прил.

соотн. с сущ. дифференциал II, связанный с ним

III прил.

1. соотн. с сущ. дифференциация, связанный с нею

2. Неодинаковый при разных условиях; различный.

3. Основанный на различии; различительный.

ДИФФЕРЕНЦИА́ЛЬНЫЙ -ая, -ое.

1. к Дифференциа́л (1 зн.). Д-ая геометрия. Д-ое исчисление.

2. Различный, неодинаковый; способствующий различию кого-, чего-л. Д. подход к проблеме. Д. тариф. Д-ая плата. Д-ые признаки видов растений.

-ая, -ое.

1. Различный, неодинаковый при разных условиях.

Дифференциальная рента. Дифференциальный тариф.

2. мат.

Относящийся к дифференциалу (в 1 знач.).

Дифференциальная геометрия (раздел геометрии, в котором геометрические образы изучаются методами математического анализа).

Дифференциальное исчисление (раздел математики, в котором изучаются производные и дифференциалы функций).

Дифференциальные уравнения (содержащие искомые функции, их производные различных порядков и независимые переменные).

Составить слова из слова дифференциальный