Элемента́рная длина́ - то же, что фундаментальная длина.
* * *
ЭЛЕМЕНТАРНАЯ ДЛИНА - ЭЛЕМЕНТА́РНАЯ ДЛИНА́, то же, что фундаментальная длина (см. ФУНДАМЕНТАЛЬНАЯ ДЛИНА).
ЭЛЕМЕНТАРНАЯ длина - то же, что фундаментальная длина.
ЭЛЕМЕНТА́РНАЯ (от лат. elementarius - первоначальный, простейший, основной) ЕДИНИ́ЦА ОБУЧЕ́НИЯ.
Минимальная структурная единица методической организации учебного материала, используемого в учебном процессе. Э. е. о. обычно считается упражнение. В отличие от урока упражнение не может дробиться на меньшие по объему единицы, что и позволяет говорить об упражнении как об Э. е. о.
Элемента́рная матема́тика - несколько неопределённое понятие, охватывающее совокупность таких разделов, задач и методов математики, в которых не пользуются общими понятиями переменной, функции, предела.
* * *
ЭЛЕМЕНТАРНАЯ МАТЕМАТИКА - ЭЛЕМЕНТА́РНАЯ МАТЕМА́ТИКА, несколько неопределенное понятие, охватывающее совокупность таких разделов, задач и методов математики, в которых не пользуются общими понятиями переменной, функции, предела.
ЭЛЕМЕНТАРНАЯ МАТЕМАТИКА - несколько неопределенное понятие, охватывающее совокупность таких разделов, задач и методов математики, в которых не пользуются общими понятиями переменной, функции, предела.
Элемента́рная яче́йка криста́лла - часть кристаллической решётки, параллельные переносы которой в трёх измерениях (трансляции) позволяют построить всю кристаллическую решётку. Выбор элементарной ячейки кристалла производится различными способами. Элементарная ячейка кристалла в общем случае имеет форму параллелепипеда. Длины рёбер обозначают a, b, с, а углы между ними - α, β, γ (рис.).
* * *
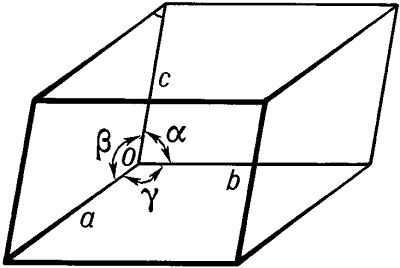
ЭЛЕМЕНТАРНАЯ ЯЧЕЙКА КРИСТАЛЛА - ЭЛЕМЕНТА́РНАЯ ЯЧЕ́ЙКА КРИСТА́ЛЛА, часть кристаллической решетки, параллельные переносы которой в трех измерениях (трансляции) позволяют построить всю кристаллическую решетку. Выбор элементарной ячейки кристалла производится различными способами. За ребра элементарной ячейки, т. е. за элементарные трансляции, принимают те направления в пространственной решетке (см. ПРОСТРАНСТВЕННАЯ РЕШЕТКА), в которых период трансляции наименьший и которые наилучшим образом отражают симметрию решетки. Если по соображениям симметрии это возможно, то предпочтение отдается трансляциям взаимно перпендикулярным и (или) таким, чтобы периоды элементарных трансляций были равны друг другу.
Выбор основных трансляций в структуре кристалла определяет кристаллографическую систему координат. Параллелепипед, построенный на трех элементарных трансляциях a, b, c называется элементарным параллелепипедом или элементарной ячейкой. В трехмерной системе координат X, Y, Z трансляции a, b, c направлены, соответственно, вдоль осей X, Y, Z, а углы элементарной ячейки a, b, g лежат против осей X, Y, Z. Направления кристаллографических осей координат соответствуют направлениям ребер элементарной ячейки, а масштабные отрезки - длинам этих ребер.
Объем примитивной элементарной ячейки не зависит от ее формы и является величиной постоянной для данной решетки, он равен объему, приходящемуся на один узел.
ЭЛЕМЕНТАРНАЯ ЯЧЕЙКА КРИСТАЛЛА - часть кристаллической решетки, параллельные переносы которой в трех измерениях (трансляции) позволяют построить всю кристаллическую решетку. Выбор элементарной ячейки кристалла производится различными способами. Элементарная ячейка кристалла в общем случае имеет форму параллелепипеда. Длины ребер обозначают a, b, c, а углы между ними - ?, ?, ?.
ЭЛЕМЕНТАРНАЯ ЯЧЕЙКА МАГНИТНАЯ - ЭЛЕМЕНТА́РНАЯ ЯЧЕ́ЙКА МАГНИ́ТНАЯ, наименьшая совокупность групп атомов кристаллической решетки, периодическим повторением которой (трансляциями) получается вся магнитная структура кристалла. Кристаллическая элементарная ячейка может или совпадать с магнитной, или быть кратной ей.
Макроскопический суммарный момент единицы объема IS называется спонтанной намагниченностью.
Все кристаллы с магнитным упорядочением подразделяются на две группы:
- кристаллы, в которых суммарный магнитный момент элементарной магнитной ячейки IS не равно 0. Эти кристаллы называют ферромагнетиками (см. ФЕРРОМАГНЕТИК).
- кристаллы, в которых суммарный магнитный моментом элементарной магнитной ячейки IS=0. Такие кристаллы являются антиферромагнетиками (см. АНТИФЕРРОМАГНЕТИК).
Кристаллографически все атомы, имеющие одинаковое направление магнитных моментов в структуре, можно объединить в магнитные подрешетки. Магнитная подрешетка - это совокупность всех атомных магнитных моментов, получающихся один из другого с помощью параллельных переносов на расстояния, кратные периодам магнитной элементарной ячейки. В общем случае магнитная структура может содержать несколько подрешеток, образованных атомами, находящимися в кристаллографически неэквивалентных позициях.