дифференциа/льно анализи/руемый
дифференциально-разностный
Орфографический словарь
Синонимы к слову дифференциально-разностный
Морфемно-орфографический словарь
Полезные сервисы
дифференциальное исчисление
Энциклопедический словарь
Дифференциа́льное исчисле́ние - раздел математики, в котором изучаются производные, дифференциалы и их применения к исследованию свойств функций. Производной функции у = f(х) называется предел отношения приращения Δу = у1 - у0 функции к приращению Δх = x1 - х0 аргумента при Δх, стремящемся к нулю (если этот предел существует).
Производная обозначается f'(х) или у'; т.о., 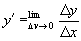 . Дифференциалом функции у = f(х) называется выражение dy = у´dx, где dx = Δх - приращение аргумента х. Очевидно, что у' = dy/dx. Отношение dy/dx часто употребляют как знак производной. Вычисление производных и дифференциалов называют дифференцированием. Если производная f'(х) имеет, в свою очередь, производную, то её называют второй производной функции f(x) и обозначают f"(х), и т. д. Основные понятия дифференциального исчисления могут быть распространены на случай функций нескольких переменных. Если z = f(х, у) - функция двух переменных х и у, то, зафиксировав для у какое-либо значение, можно дифференцировать z по х; полученная производная
. Дифференциалом функции у = f(х) называется выражение dy = у´dx, где dx = Δх - приращение аргумента х. Очевидно, что у' = dy/dx. Отношение dy/dx часто употребляют как знак производной. Вычисление производных и дифференциалов называют дифференцированием. Если производная f'(х) имеет, в свою очередь, производную, то её называют второй производной функции f(x) и обозначают f"(х), и т. д. Основные понятия дифференциального исчисления могут быть распространены на случай функций нескольких переменных. Если z = f(х, у) - функция двух переменных х и у, то, зафиксировав для у какое-либо значение, можно дифференцировать z по х; полученная производная 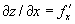 называется частной производной z по х. Аналогично определяются частная производная
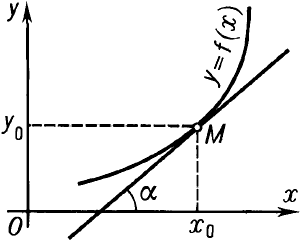
называется частной производной z по х. Аналогично определяются частная производная 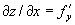 , частные производные высших порядков, частные и полные дифференциалы. Для приложений дифференциального исчисления к геометрии важно, что так называемый угловой коэффициент касательной, то есть тангенс угла α (см. рис.) между осью Ох и касательной к кривой у = f(х) в точке М(х0, у0), равен значению производной при х = х0, то есть f'(х0). В механике скорость прямолинейно движущейся точки можно истолковать как производную пути по времени. Дифференциальное исчисление (как и интегральное исчисление) имеет многочисленные применения.
, частные производные высших порядков, частные и полные дифференциалы. Для приложений дифференциального исчисления к геометрии важно, что так называемый угловой коэффициент касательной, то есть тангенс угла α (см. рис.) между осью Ох и касательной к кривой у = f(х) в точке М(х0, у0), равен значению производной при х = х0, то есть f'(х0). В механике скорость прямолинейно движущейся точки можно истолковать как производную пути по времени. Дифференциальное исчисление (как и интегральное исчисление) имеет многочисленные применения.
* * *
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ - ДИФФЕРЕНЦИА́ЛЬНОЕ ИСЧИСЛЕ́НИЕ, раздел математики, в котором изучаются производные, дифференциалы и их применения к исследованию свойств функций.
Производной функции y = f(х) называется предел отношения приращения Dy = y1 - y0 функции к приращению Dx = x1 - x0 аргумента при Dx, стремящемся к нулю (если этот предел существует). Дифференциалом функции y = f(x) называется выражение dy = yўdx, где dx = Dx - приращение аргумента x. Очевидно, что yў = dy/dx. Отношение dy/dx часто употребляют как знак производной. Вычисление производных и дифференциалов называют дифференцированием. Если производная fў(x) имеет, в свою очередь, производную, то ее называют 2-й производной функции f(x) и обозначают fўў(x), и т. д. Основные понятия дифференциального исчисления могут быть распространены на случай функций нескольких переменных. Если z = f(x,y) - функция двух переменных x и y, то, зафиксировав для y какое-либо значение, можно дифференцировать z по x; полученная производная dz/dx = fўx называется частной производной z по x. Аналогично определяются частная производная dz/dy = fўy, частные производные высших порядков, частные и полные дифференциалы.
Для приложений дифференциального исчисления к геометрии важно, что т. н. угловой коэффициент касательной, т. е. тангенс угла a между осью Ox и касательной к кривой y = f(x) в точке M(x0, y0), равен значению производной при x = x0, т. е. fў(x0). В механике скорость прямолинейно движущейся точки можно истолковать как производную пути по времени. Дифференциальное исчисление (как и интегральное исчисление (см. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ)) имеет многочисленные применения.
Большой энциклопедический словарь
ДИФФЕРЕНЦИАЛЬНОЕ исчисление - раздел математики, в котором изучаются производные, дифференциалы и их применения к исследованию свойств функций. Производной функции y = f(х) называется предел отношения приращения ?y = y1 - y0 функции к приращению ?x = x1 - x0 аргумента при ?x, стремящемся к нулю (если этот предел существует). производная обозначается f?(x) или y?; таким образом, Дифференциалом функции y = f(x) называется выражение dy = y?dx, где dx = ?x - приращение аргумента x. Очевидно, что y? = dy/dx. Отношение dy/dx часто употребляют как знак производной.
Вычисление производных и дифференциалов называют дифференцированием. Если производная f?(x) имеет, в свою очередь, производную, то ее называют 2-й производной функции f(x) и обозначают f??(x), и т. д. Основные понятия дифференциального исчисления могут быть распространены на случай функций нескольких переменных. Если z = f(x,y) - функция двух переменных x и y, то, зафиксировав для y какое-либо значение, можно дифференцировать z по x; полученная производная dz/dx = f?x называется частной производной z по x. Аналогично определяются частная производная dz/dy = f?y, частные производные высших порядков, частные и полные дифференциалы. Для приложений дифференциального исчисления к геометрии важно, что т. н. угловой коэффициент касательной, т. е. тангенс угла ? (см. рис.) между осью Ox и касательной к кривой y = f(x) в точке M(x0, y0), равен значению производной при x = x0, т. е. f?(x0). В механике скорость прямолинейно движущейся точки можно истолковать как производную пути по времени. Дифференциальное исчисление (как и интегральное исчисление) имеет многочисленные применения.
Иллюстрированный энциклопедический словарь
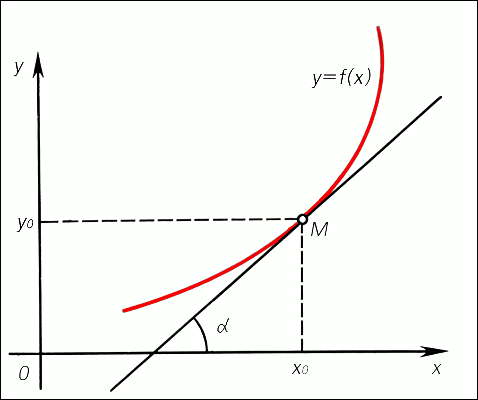
Дифференциальное исчисление. Проведение касательной к графику функции y=f(x) в точке M.
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ, раздел математики, в котором изучаются производные, дифференциалы и их применения к исследованию свойств функций. Производной функции y=f(x) называется предел отношения приращения функции Dy=y1-y0 к приращению аргумента Dx=x1-x0 при Dx, стремящемся к нулю (если этот предел существует). Производная обозначается y'' т.о. y'=lim Dy/Dx при Dx®0. Дифференциалом функции y=f(x) называется выражение dy=y', где dx=y'Dx - приращение аргумента x. Очевидно, что y'=dy/dx. Отношение dy/dx часто употребляют как знак производной. Вычисление производных и дифференциалов называется дифференцированием. Если производная f' (x) имеет, в свою очередь, производную, то ее называют 2-й производной функции f (x) и обозначают f" (x), и т.д. Основные понятия дифференциального исчисления могут быть распространены на случай функций нескольких переменных. Для приложений дифференциального исчисления к геометрии важно, что так называемый угловой коэффициент касательной, т.е. тангенс угла a между осью Ox и касательной к кривой y=f(x) в точке M(x0, y0), равен значению производной при x=x0, т.е. f' (x0). С точки зрения механики производную от пути по времени можно истолковать как скорость прямолинейно движущейся точки. Дифференциальное исчисление (как и интегральное исчисление) имеет многочисленные применения.
Словарь иностранных слов
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ - математическая наука, занимающаяся изучением дифференциалов функций, т. е. выражений, показывающих, в какой зависимости переменные величины находятся друг от друга. Дифференциалом функции назыв. бесконечно малое приращение, получаемое ею, соответственно бесконечно малому приращению переменной величины.
Полезные сервисы
дифференциальное счисление
дифференциальное уравнение
Энциклопедический словарь
Дифференциа́льное уравне́ние - уравнение, связывающее искомую функцию, её производные (или дифференциалы) и независимые переменные, например dy = 2xdx. Решением или интегралом дифференциального уравнения называется функция, при подстановке которой в дифференциальном уравнении последнее обращается в тождество; в приведённом примере решением является всякая функция вида у = х2 + С, где С - любая постоянная. Процесс решения дифференциального уравнения называется его интегрированием. При помощи дифференциального уравнения записываются многие реальные процессы, поэтому дифференциальные уравнения имеют исключительно важное значение для естествознания и техники.
* * *
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ - ДИФФЕРЕНЦИА́ЛЬНОЕ УРАВНЕ́НИЕ, уравнение, связывающее искомую функцию, ее производные (или дифференциалы) и независимые переменные, напр. dy = 2xdx. Решением или интегралом дифференциального уравнения называется функция, при подстановке которой в дифференциальное уравнение последнее обращается в тождество; в приведенном примере решением является всякая функция вида y = x2 + C, где С - любая постоянная. Процесс решения дифференциального уравнения называется его интегрированием. При помощи дифференциального уравнения записываются многие реальные процессы, поэтому дифференциальные уравнения имеют исключительно важное значение для естествознания и техники.
Большой энциклопедический словарь
ДИФФЕРЕНЦИАЛЬНОЕ уравнение - уравнение, связывающее искомую функцию, ее производные (или дифференциалы) и независимые переменные, напр. dy = 2xdx. Решением или интегралом дифференциального уравнения называется функция, при подстановке которой в дифференциальное уравнение последнее обращается в тождество; в приведенном примере решением является всякая функция вида y = x2 + C, где С - любая постоянная. Процесс решения дифференциального уравнения называется его интегрированием. При помощи дифференциального уравнения записываются многие реальные процессы, поэтому дифференциальные уравнения имеют исключительно важное значение для естествознания и техники.