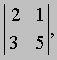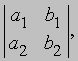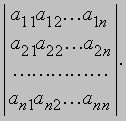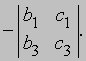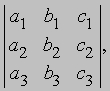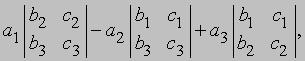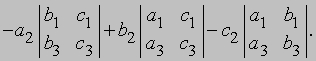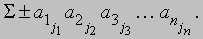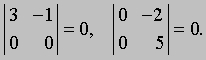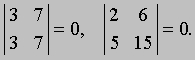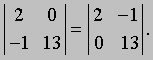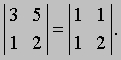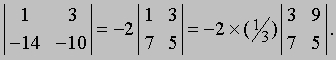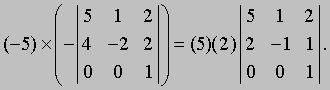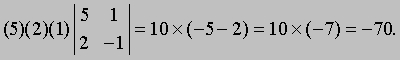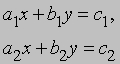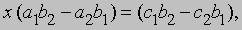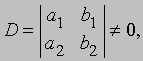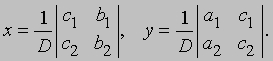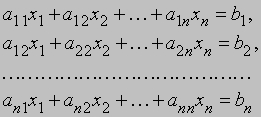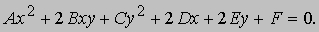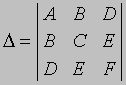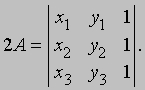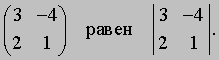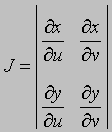ОПРЕДЕЛИ́ТЕЛЬ -я; м.
1. Книжн. То, чем определяется, обусловливается что-л. Звук может быть определителем скорости. Главным определителем времени является движение Солнца в космическом пространстве.
2. Спец. Руководство (книга или таблица) для определения чего-л. О. растений. О. рыб.
3. Матем. Математическое выражение, с помощью которого можно просто и кратко сформулировать правила решения и исследования алгебраических уравнений первой степени.
* * *
определи́тель (детерминант), составленное по определенному правилу из n2 чисел математическое выражение, применяемое при решении и исследовании систем алгебраических уравнений 1-й степени. Число n называется порядком определитель. Так, определитель. 2-го порядка, составленный из четырёх чисел a1, b1, а2, b2, обозначается
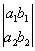 1, b2, b1, a2.
1, b2, b1, a2.
* * *
ОПРЕДЕЛИТЕЛЬ - ОПРЕДЕЛИ́ТЕЛЬ (детерминант), составленное по определенному правилу из n2 чисел математическое выражение, применяемое при решении и исследовании систем алгебраических уравнений 1-й степени. Число n называется порядком определителя. Так, определитель 2-го порядка, составленный из четырех чисел a1, b1, a2, b2, обозначается:
и равен a1b2-b1a2.
ОПРЕДЕЛИТЕЛЬ - или детерминант, - в математике запись чисел в виде квадратной таблицы, в соответствие которой ставится другое число ("значение" определителя). Очень часто под понятием "определитель" имеют в виду как значение определителя, так и форму его записи. Определители позволяют удобно записывать сложные выражения, возникающие, например, при решении линейных уравнений в аналитической геометрии и в математическом анализе. Открытие определителей приписывают японскому математику С. Кова (1683) и, независимо, Г. Лейбницу (1693). Современная теория восходит к работам Ж. Бине, О. Коши и К. Якоби в начале 19 в. Простейший определитель состоит из 4 чисел, называемых элементами и расположенных в виде 2-х строк и 2-х столбцов. О таком определителе говорят, что он 2-го порядка. Например, таков определитель
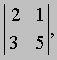
значение которого равно 2*5 - 3*1 (т.е. 10 - 3 или 7). В общем случае определитель 2-го порядка принято записывать в виде
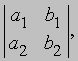
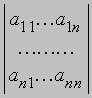
а его значение равно a1b2 - a2b1, где a и b - числа или функции. Определитель 3-го порядка состоит из 9 элементов, расположенных в виде 3-х строк и 3-х столбцов. В общем случае определитель n-го порядка состоит из n2 элементов, и обычно его записывают как
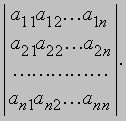
Первый индекс каждого элемента указывает номер строки, второй - номер столбца, на пересечении которых стоит этот элемент, поэтому aij - элемент i-й строки и j-го столбца. Часто такой определитель записывают в виде |aij|. Один из методов вычисления определителя, почти всегда используемый при вычислении определителей высокого порядка, состоит в разложении по "минорам". Минором, соответствующим любому элементу определителя, называется определитель меньшего на 1 порядка, получаемый из исходного вычеркиванием строки и столбца, на пересечении которых стоит этот элемент. Например, минором, соответствующим элементу a2 из определителя

"Алгебраическим дополнением" элемента называется его минор, взятый со знаком плюс, если сумма номеров строки и столбца, на пересечении которых стоит элемент, четна, и со знаком минус, если она нечетна. В приведенном выше примере элемент a2 состоит в 1-м столбце и во 2-й строке; сумма (1 + 2) нечетна, и поэтому алгебраическое дополнение элемента a2 равно его минору, взятому со знаком минус, т.е.
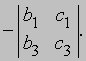
Значение определителя равно сумме произведений элементов любой строки (или любого столбца) на их алгебраические дополнения. Например, определитель
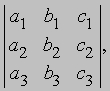
разложенный по первому столбцу, имеет вид
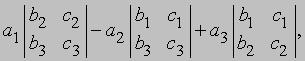
а его разложение по второй строке, имеет вид
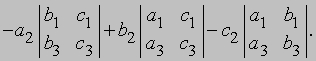
Вычислив каждый минор и умножив его на коэффициент, нетрудно убедиться в том, что оба выражения совпадают. Значение определителя. Под значением определителя
принято понимать сумму всех произведений из n элементов, т.е.
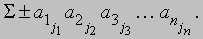
В этой формуле суммирование ведется по всем перестановкам j1, ј, jn чисел 1, 2, ј, n и перед членом ставится знак плюс, если перестановка четна, и минус, если эта перестановка нечетна. Такая сумма насчитывает ровно n! членов, половина которых берется со знаком плюс, половина - со знаком минус. Каждый член суммы содержит по одному члену из каждого столбца и каждой строки определителя. Можно доказать, что эта сумма совпадает с выражением, получаемым при разложении определителя по минорам.
Свойства определителя. Среди наиболее важных свойств определителя назовем следующие. (i) Если все элементы любой строки (или любого столбца) равны нулю, то и значение определителя равно нулю:
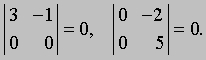
(ii) Если элементы двух строк (или двух столбцов) равны или пропорциональны, то значение определителя равно нулю:
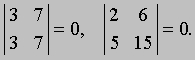
(iii) Значение определителя не изменится, если все его строки и столбцы поменять местами, т.е. записать первую строку в виде первого столбца, вторую строку - в виде второго столбца и т.д. (такая операция называется транспонированием). Например,
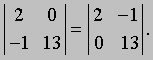
(iv) Значение определителя не изменится, если к элементам одной строки (или столбца) прибавить соответствующие элементы другой строки (или столбца), умноженные на произвольный множитель. В следующем примере элементы второй строки умножаются на -2 и прибавляются к элементам первой строки:
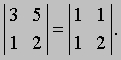
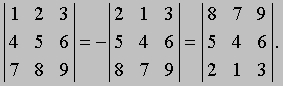
(v) Если поменять местами две строки (или два столбца), то определитель изменит знак:
(vi) Если все элементы одной строки (или одного столбца) содержат общий множитель, то этот множитель можно вынести за знак определителя:
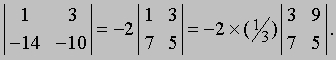
Пример. Вычислим значение следующего определителя 4-го порядка:

Прибавим к 1-й строке 4-ю строку:
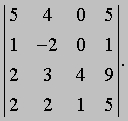
Вычтем 1-й столбец из 4-го столбца:

Умножим 3-й столбец на 3 и вычтем из 4-го столбца:

Если угодно, то строки и столбцы можно поменять местами:

Разложим определитель по элементам четвертой строки. Три элемента этой строки равны нулю, ненулевой элемент стоит в третьем столбце, а поскольку сумма (3 + 4) нечетна, его алгебраическое дополнение имеет знак минус. В результате получаем:
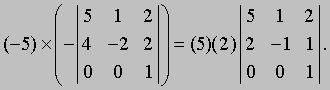
Минор можно разложить по элементам третьей строки: два ее элемента равны нулю, а отличный от нуля элемент стоит в третьем столбце; сумма (3 + 3) четна, поэтому предыдущее равенство можно продолжить:
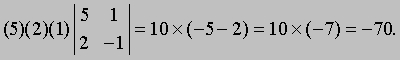
Применения. Решение системы уравнений
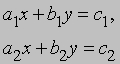
можно получить, если первое уравнение умножить на b2, второе - на b1, а затем вычесть одно уравнение из другого. Проделав эти операции, мы получим
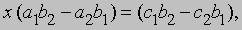
или, если
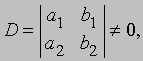
то
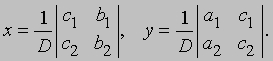
Такая запись решения с помощью определителей допускает обобщение на случай решения системы n линейных уравнений с n неизвестными; каждый определитель будет n-го порядка. Определителем системы линейных уравнений
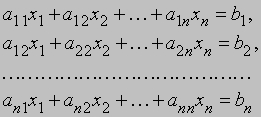
будет

Заметим, что если D = 0, то уравнения либо несовместны, либо не являются независимыми. Поэтому предварительное вычисление определителя D позволяет проверить, разрешима ли система линейных уравнений.
Определители в аналитической геометрии. Общее уравнение конического сечения представимо в виде
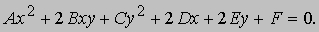
Определитель
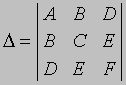
называется дискриминантом. Если D = 0, то кривая вырождается в пару параллельных или пересекающихся прямых либо в точку (см. также КОНИЧЕСКИЕ СЕЧЕНИЯ). Другой пример: площадь треугольника A с вершинами в точках (обход - против часовой стрелки) (x1, y1), (x2, y2) и (x3, y3) определяется выражением
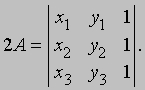
Связь определителей с матрицами. Матрицей называется запись массива чисел в виде прямоугольной таблицы. Определители связаны с квадратными матрицами; например, определитель матрицы
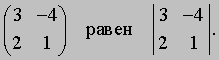
Если A, B и С - квадратные матрицы и , то |A|*|B| = |C|.
См. также АЛГЕБРА АБСТРАКТНАЯ.
Якобиан. Если x = f (u, v), y = g (u, v) - преобразование координат, то определитель
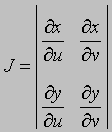
называется якобианом или определителем Якоби этого преобразования. Если J не равен 0 в некоторой точке, то в ее окрестности уравнения преобразования можно однозначно разрешить относительно u и v, представив их как функции от x и y.
См. МАТЕМАТИЧЕСКИЙ АНАЛИЗ.
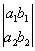 1, b2, b1, a2.
1, b2, b1, a2.