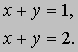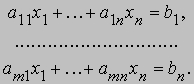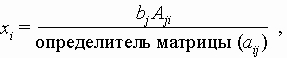Уравнением называется математическое соотношение, выражающее равенство двух алгебраических выражений. Если равенство справедливо для любых допустимых значений входящих в него неизвестных, то оно называется тождеством; например, соотношение вида (x - 1)2 = (x - 1)(x - 1) выполняется при всех значениях переменной x. Для обозначения тождества часто вместо обычного знака равенства = пишут знак є, который читается "тождественно равно". Тождества используются в алгебре при записи разложения многочленов на множители (как в приведенном выше примере). Встречаются они и в тригонометрии в таких соотношениях, как sin2x + cos2x = 1, а в общем случае выражают формальное отношение между двумя на первый взгляд различными математическими выражениями. Если уравнение, содержащее переменную x, выполняется только при определенных, а не при всех значениях x, как в случае тождества, то может оказаться полезным определить те значения x, при которых это уравнение справедливо. Такие значения x называются корнями или решениями уравнения. Например, число 5 является корнем уравнения 2x + 7= 17. Уравнения служат мощным средством решения практических задач. Точный язык математики позволяет просто выразить факты и соотношения, которые, будучи изложенными обычным языком, могут показаться запутанными и сложными. Неизвестные величины, обозначаемые в задаче символами, например x, можно найти, сформулировав задачу на математическом языке в виде уравнений. Методы решения уравнений составляют в основном предмет того раздела математики, который называется теорией уравнений.
ТИПЫ УРАВНЕНИЙ
Алгебраические уравнения. Уравнения вида fn = 0, где fn - многочлен от одной или нескольких переменных, называются алгебраическими уравнениями. Многочленом называется выражение вида fn = a0 xiyj... vk + a1 xlym... vn + ј + asxpyq... vr, где x, y, ..., v - переменные, а i, j, ..., r - показатели степеней (целые неотрицательные числа). Многочлен от одной переменной записывается так: f(x) = a0xn + a1xn - 1 + ... + an - 1x + an или, в частном случае, 3x4 - x3 + 2x2 + 4x - 1. Алгебраическим уравнением с одним неизвестным называется любое уравнение вида f(x) = 0. Если a0 № 0, то n называется степенью уравнения. Например, 2x + 3 = 0 - уравнение первой степени; уравнения первой степени называются линейными, так как график функции y = ax + b имеет вид прямой. Уравнения второй степени называются квадратными, а уравнения третьей степени - кубическими. Аналогичные названия имеют и уравнения более высоких степеней.
Трансцендентные уравнения. Уравнения, содержащие трансцендентные функции, такие, как логарифмическая, показательная или тригонометрическая функция, называются трансцендентными. Примером могут служить следующие уравнения:
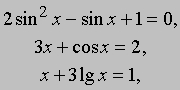
где lg - логарифм по основанию 10.
Дифференциальные уравнения. Так называются уравнения, содержащие одну или несколько функций и их производные или дифференциалы. Дифференциальные уравнения оказались исключительно ценным средством точной формулировки законов природы.
Интегральные уравнения. Уравнения, содержащие неизвестную функцию под знаком интеграла, например, f (s) = тK (s, t) f (t) dt, где f (s) и K(s,t) заданы, а f (t) требуется найти.
Диофантовы уравнения. Диофантовым уравнением называется алгебраическое уравнение с двумя или более неизвестными с целыми коэффициентами, решение которого ищется в целых или рациональных числах. Например, уравнение 3x - 5y = 1 имеет решение x = 7, y = 4; вообще же его решениями служат целые числа вида x = 7 + 5n, y = 4 + 3n.
РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Для всех перечисленных выше типов уравнений общих методов решения не существует. И все же во многих случаях, особенно для алгебраических уравнений определенного типа, имеется достаточно полная теория их решения.
Линейные уравнения. Эти простые уравнения решаются путем их сведения к эквивалентному уравнению, из которого непосредственно видно значение неизвестного. Например, уравнение x + 2 = 7 можно свести к эквивалентному уравнению x = 5 вычитанием числа 2 из правой и левой частей. Шаги, совершаемые при сведении простого уравнения, например, x + 2 = 7, к эквивалентному, основаны на использовании четырех аксиом. 1. Если равные величины увеличить на одно и то же число, то результаты будут равны. 2. Если из равных величин вычесть одно и то же число, то результаты будут равны. 3. Если равные величины умножить на одно и то же число, то результаты будут равны. 4. Если равные величины разделить на одно и то же число, то результаты будут равны. Например, чтобы решить уравнение 2x + 5 = 15, мы воспользуемся аксиомой 2 и вычтем число 5 из правой и левой частей, в результате чего получим эквивалентное уравнение 2x = 10. Затем мы воспользуемся аксиомой 4 и разделим обе части полученного уравнения на 2, в результате чего исходное уравнение сведется к виду x = 5, что и является искомым решением.
Квадратные уравнения. Решения общего квадратного уравнения ax2 + bx + c = 0 можно получить с помощью формулы
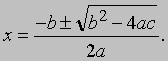
Таким образом, существуют два решения, которые в частном случае могут совпадать.
Другие алгебраические уравнения. Явные формулы, аналогичные формуле для решения квадратного уравнения, можно выписать только для уравнений третьей и четвертой степеней. Но и эти формулы сложны и далеко не всегда помогают легко находит корни. Что же касается уравнений пятой степени или выше, то для них, как доказал Н.Абель в 1824, нельзя указать общую формулу, которая выражала бы корни уравнения через его коэффициенты при помощи радикалов. В отдельных частных случаях уравнения высших степеней удается легко решить, факторизуя их левую часть, т.е. разлагая ее на множители. Например, уравнение x3 + 1 = 0 можно записать в факторизованном виде (x + 1)(x2 - x + 1) = 0. Решения мы находим, полагая каждый из множителей равным нулю:
Таким образом, корни равны x = -1,
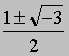 т.е. всего 3 корня. Если уравнение не факторизуется, то следует воспользоваться приближенными решениями. Основные методы нахождения приближенных решений были разработаны Горнером, Ньютоном и Греффе. Однако во всех случаях существует твердая уверенность в том, что решение существует: алгебраическое уравнение n-й степени имеет ровно n корней." alt=", т.е. всего 3 корня. Если уравнение не факторизуется, то следует воспользоваться приближенными решениями. Основные методы нахождения приближенных решений были разработаны Горнером, Ньютоном и Греффе. Однако во всех случаях существует твердая уверенность в том, что решение существует: алгебраическое уравнение n-й степени имеет ровно n корней.">
т.е. всего 3 корня. Если уравнение не факторизуется, то следует воспользоваться приближенными решениями. Основные методы нахождения приближенных решений были разработаны Горнером, Ньютоном и Греффе. Однако во всех случаях существует твердая уверенность в том, что решение существует: алгебраическое уравнение n-й степени имеет ровно n корней." alt=", т.е. всего 3 корня. Если уравнение не факторизуется, то следует воспользоваться приближенными решениями. Основные методы нахождения приближенных решений были разработаны Горнером, Ньютоном и Греффе. Однако во всех случаях существует твердая уверенность в том, что решение существует: алгебраическое уравнение n-й степени имеет ровно n корней.">
, т.е. всего 3 корня. Если уравнение не факторизуется, то следует воспользоваться приближенными решениями. Основные методы нахождения приближенных решений были разработаны Горнером, Ньютоном и Греффе. Однако во всех случаях существует твердая уверенность в том, что решение существует: алгебраическое уравнение n-й степени имеет ровно n корней.
Системы линейных уравнений. Два линейных уравнения с двумя неизвестными можно записать в виде
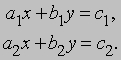
Решение такой системы находится с помощью определителей
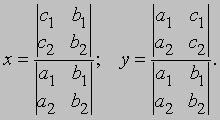
Оно имеет смысл, если
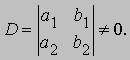
Если же D = 0, то возможны два случая. (1) По крайней мере один из определителей
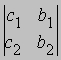 и
и 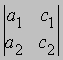
отличен от нуля. В этом случае решения уравнений не существует;
уравнения несовместны. Численный пример такой ситуации - система
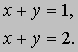
(2) Оба определителя равны нулю. В этом случае второе уравнение просто кратно первому и существует бесконечное
число решений. Общая теория рассматривает m линейных уравнений с n переменными:
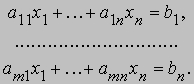
Если m = n и матрица (aij) невырожденна, то решение единственно и может быть найдено по правилу Крамера:
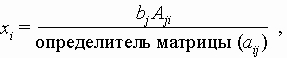
где Aji - алгебраическое дополнение элемента aij в матрице (aij). В более общем плане существуют следующие теоремы.
Пусть r - ранг матрицы (aij), s - ранг окаймленной матрицы (aij; bi), которая получается из aij присоединением столбца
из чисел bi. Тогда: (1) если r = s, то существует n - r линейно независимых решений; (2) если r < s, то уравнения
несовместны и решений не существует.
См. также АЛГЕБРА.
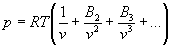 ,
,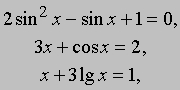
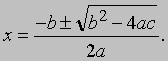
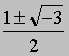 т.е.
т.е. 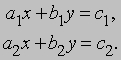
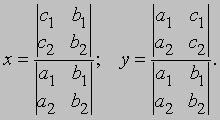
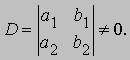
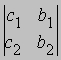 и
и