аэр/о/дина́м/ик/.
аэродинамика
Толковый словарь
ж.
Раздел аэромеханики, изучающий законы движения воздуха и других газов и силы, возникающие на обтекаемых ими телах.
Толковый словарь Ушакова
АЭРОДИНА́МИКА, аэродинамики, мн. нет, жен. (от греч. aer - воздух и dynamis - сила) (научн.). Учение о сопротивлении воздуха при движении тел.
Толковый словарь Ожегова
АЭРОДИНА́МИКА, -и, жен. Раздел аэромеханики, изучающий движение воздуха и других газов и взаимодействие газов с обтекаемыми ими телами.
| прил. аэродинамический, -ая, -ое. А. нагрев (повышение температуры тела, движущегося с большой скоростью в воздухе или другом газе).
Энциклопедический словарь
АЭРОДИНА́МИКА -и; м. Раздел аэромеханики, изучающий законы движения воздуха и других газов и силы, возникающие на обтекаемых ими телах.
◁ Аэродинами́ческий, -ая, -ое. А-ая сила. А-ая труба (установка для наглядного изучения явлений, связанных с воздействием воздушного потока на физическое тело).
* * *
аэродина́мика - раздел аэромеханики, в котором изучаются законы движения газа (например, воздуха) и силы, возникающие на поверхности обтекаемого газом тела. Сформировалась в XX в. в связи с развитием авиации. Основные задачи аэродинамики: определение сил, действующих на обтекаемое газом тело, распределения давления на его поверхности и скоростей в газе, его обтекающем.
* * *
АЭРОДИНАМИКА - АЭРОДИНА́МИКА, раздел аэромеханики, в котором изучаются законы движения газа (напр., воздуха) и силы, возникающие на поверхности обтекаемого газом тела. Сформировалась в 20 в. в связи с развитием авиации. Основные задачи аэродинамики: определение сил, действующих на обтекаемое газом тело, распределение давления на его поверхности и скоростей в газе, его обтекающем.
Большой энциклопедический словарь
АЭРОДИНАМИКА - раздел аэромеханики, в котором изучаются законы движения газа (напр., воздуха) и силы, возникающие на поверхности обтекаемого газом тела. Сформировалась в 20 в. в связи с развитием авиации. Основные задачи аэродинамики: определение сил, действующих на обтекаемое газом тело, распределение давления на его поверхности и скоростей в газе, его обтекающем.
Академический словарь
-и, ж.
Часть аэромеханики, изучающая законы движения воздуха и др. газов и воздействие газов на обтекаемые ими тела.
Энциклопедия Кольера
АЭРОДИНАМИКА - раздел механики сплошных сред, в котором изучаются закономерности движения воздуха и других газов, а также характеристики тел, движущихся в воздухе. К аэродинамическим характеристикам тел относятся подъемная сила и сила сопротивления и их распределения по поверхности, а также тепловые потоки к поверхности тела, вызванные его движением в воздухе. В аэродинамике рассматриваются такие тела, как самолеты, ракеты, воздушно-космические летательные аппараты и автомобили. В атмосферной аэродинамике изучаются процессы диффузии твердых частиц (например, дыма, смога, пыли) в атмосфере и аэродинамические силы, действующие на здания и другие сооружения. Ниже рассматриваются проблемы, связанные с движением летательных аппаратов, однако те же принципы можно применить к описанию других явлений, изучаемых в общей гидроаэромеханике. Здесь изложены физические законы, управляющие движениями воздуха, и концепции, необходимые для понимания механизмов возникновения подъемной силы и силы сопротивления при различных скоростях полета, включая течения с ударными волнами. На очень больших высотах (свыше 60 км) вследствие очень низкой плотности воздуха возникают некоторые изменения картины обтекания тела.
ХАРАКТЕРИСТИКИ ВОЗДУХА И ДРУГИХ ТЕКУЧИХ СРЕД
В аэродинамике принимаются во внимание такие свойства воздуха, как плотность, давление, температура и молекулярный состав. Воздух состоит из молекул ряда химических элементов, в основном азота (78%) и кислорода (21%). Имеются также небольшие примеси аргона, углекислого газа, водорода и других газов. Число молекул в единице объема воздуха чрезвычайно велико: на уровне моря при температуре 15° С в 1 м3 содержится 2,7Ч1025 молекул. Плотность определяется как масса воздуха, содержащегося в единице объема. Давление представляет собой силу, действующую на единицу площади. Молекулы воздуха находятся в непрерывном движении; они соударяются с ограничивающей воздух поверхностью и отражаются от нее. Сумма всех импульсов, сообщаемых молекулами, падающими на единицу площади поверхности за единицу времени, равна давлению.
Температура воздуха (или какого-либо другого газа) служит мерой средней кинетической энергии молекул (равной половине произведения массы на квадрат скорости), отнесенной к единице массы. Важной физической характеристикой газа, зависящей только от температуры, является скорость звука. Скорость звука a (м/с) в воздухе можно вычислить, зная абсолютную температуру T (K), по формуле . Связь между давлением p, плотностью r и абсолютной температурой T дается формулой p = rRT, где R - газовая постоянная, равная 287,14 м2/с2ЧК для воздуха. Из этой формулы следует закон Бойля, согласно которому при постоянной температуре p/r = const, т.е. изменение плотности прямо пропорционально изменению давления. Изменения давления и плотности воздуха по высоте согласуются с этими законами. Давление и плотность уменьшаются, по сравнению с их значениями на уровне моря, в 2 раза на высоте 6 км, в 5 раз на высоте 12 км и в 100 раз на высоте 30 км. В нижних слоях атмосферы температура воздуха также снижается при увеличении высоты. Стандартная температура на уровне моря составляет 288 К. Она уменьшается до 256 К на высоте 5 км и до 217 К на высоте 12 км. Важной характеристикой движущейся среды является ее вязкость. Вязкость проявляется через свойство прилипания текучей среды к поверхности, тогда как невязкая среда свободно скользит вдоль обтекаемой поверхности. Чтобы проиллюстрировать влияние вязкости, порождающей силу, замедляющую течение (силу сопротивления), рассмотрим две большие параллельные друг другу пластины A и B (рис. 1), одна из которых движется относительно другой. Вязкая среда прилипает к каждой из пластин. Случайные движения молекул создают эффект "перемешивания", стремящегося выровнять средние скорости течения, скорость которого на пластине B равна V, а на пластине A - нулю. Результирующее распределение скоростей также приведено на рис. 1, где длина стрелок пропорциональна величине скорости в данной точке течения по высоте между пластинами. Таким образом, на движущуюся пластину B действует сила, тормозящая ее движение. Чтобы обеспечить движение пластины B при наличии торможения, к ней должна быть приложена противодействующая сила. Такая же сила стремится привести в движение пластину A.
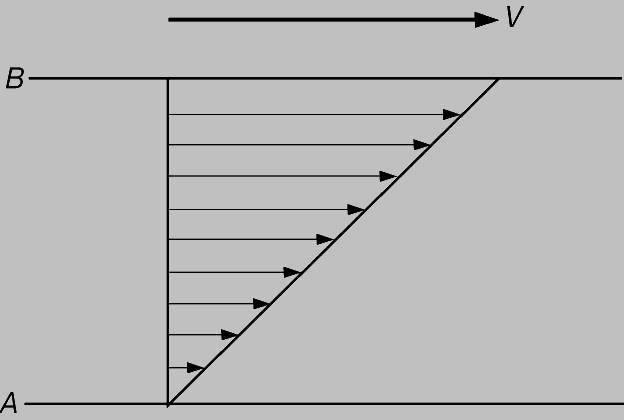
Рис. 1. СИЛА ВЯЗКОГО СОПРОТИВЛЕНИЯ, или влияние вязкости течения на пластины A и B. Пластина B движется по отношению к пластине A со скоростью V, изображенной стрелкой. Распределение скоростей жидкости между пластинами также показано соответствующими стрелками.
Величина силы, необходимой для поддержания движения пластины B со скоростью 1 м/с (или удержания на месте неподвижной пластины A), при условии, что расстояние между пластинами равно 1 м, а площадь каждой из них - 1 м2, называется коэффициентом вязкости m. Для воздуха при температуре 0° С и давлении 1 атм m = 1,73*10-5 H*c/м2. Эксперименты показывают, что коэффициент вязкости воздуха изменяется в зависимости от температуры пропорционально T0,76.
ФУНДАМЕНТАЛЬНЫЕ ЗАКОНЫ
Аэродинамика описывается фундаментальными физическими законами механики сплошных сред. Эти законы называются "законами сохранения", так как они выражают свойство сохранения массы, энергии и импульса для каждого элементарного объема движущейся среды. При использовании законов сохранения важную роль играет принцип относительности движения, сформулированный Галилео Галилеем (1564-1642), согласно которому сила, действующая на тело в воздушном потоке, зависит только от относительной скорости движений тела и воздуха и не зависит от того, движется ли тело в покоящемся воздухе или же воздух движется относительно неподвижного тела. Применим законы сохранения не к отдельным молекулам, а к некоторому движущемуся элементарному объему среды, содержащему большое число молекул. Этот упрощенный подход представляется неизбежным, если вспомнить, что молекулы, помимо своего перемещения вместе с течением, совершают случайные движения, и законы, описывающие эти движения, должны учитывать столкновения между различными молекулами, в которых изменяются их направления движения, скорости и т. д. Рассмотрим, например, элементарный объем в форме кубика со стороной 0,01 мм, объем которого равен 10-6 мм3. В этом малом объеме все еще содержится 2,7*10 10 молекул, и каждая из них движется случайно. Однако вследствие того, что объем содержит большое число молекул, он будет перемещаться со средней скоростью вдоль линий тока течения, изображенных на рис. 2.
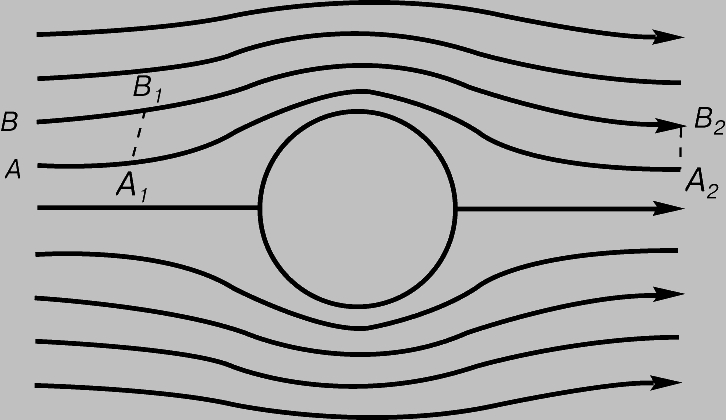
Рис. 2. ЛИНИИ ТОКА при обтекании цилиндра. Между линиями тока A и B расход (массовый поток) воздуха через линию A1B1 равен расходу через линию A2B2.
Согласно другому условию, этот элементарный объем должен быть настолько мал, чтобы средние скорости в каждой его точке можно было считать приблизительно одинаковыми. Например, если рассматривается обтекание сферы диаметром 10 мм, то элементарный кубик со стороной 0,01 мм будет достаточно малым для того, чтобы он рассматривался как одно целое, перемещающееся вдоль линии тока. Таким образом, мы рассматриваем элементарный объем среды, который достаточно велик для того, чтобы в нем содержалось большое число молекул, и достаточно мал по сравнению с "характерным масштабом" течения. На очень больших высотах, где плотность воздуха мала, понятие частицы среды теряет смысл, и приходится рассматривать движения отдельных молекул. Линии тока течения определяются как траектории частиц текущей среды. Линии тока могут быть визуализированы с помощью струек дыма, вдуваемого в воздушный поток. В применении к рассматриваемым частицам текущей среды закон сохранения массы означает, что массовый поток воздуха, проходящего между линиями тока A и B на рис. 2, один и тот же, в каком бы месте он ни измерялся. Следовательно, поток воздуха через линию A1B1 такой же, как поток воздуха через линию A2B2. Этот закон называется еще уравнением неразрывности, и течение, удовлетворяющее этому условию, называется непрерывным течением. Закон сохранения импульса является выражением второго закона Ньютона в применении к частицам текущей среды. Он может быть записан в следующей форме: Сила = Изменение импульса за секунду. Следствием этого закона является связь между давлением p, плотностью r и скоростью v. Если скорость течения достаточно мала (так что плотность можно считать постоянной всюду в поле течения), то выполняется следующее простое соотношение: p + 1/2 rv2 = const. Эта формула, известная как закон Бернулли, была получена швейцарским математиком и инженером Даниилом Бернулли (1700-1782). Течение, которое удовлетворяет этому уравнению, называется несжимаемым, поскольку оно применимо как к жидкостям, которые практически несжимаемы, так и к газам, если скорости их движения малы по сравнению со скоростью звука. Если скорость в какой-либо точке потока больше половины скорости звука, то расчеты по этой формуле будут содержать значительные погрешности. Такие течения называются сжимаемыми. Третий закон сохранения, используемый для описания деталей поля течения, выражает условие сохранения энергии. Применительно к течениям можно рассматривать два рода кинетической энергии: энергию, связанную с основным (упорядоченным) течением, и энергию, соответствующую случайным движениям молекул. Энергию, связанную со структурой отдельных молекул и атомов, мы рассматривать не будем, так как ее влияние становится заметным лишь при очень высоких температурах. В расчете на единицу объема кинетическая энергия упорядоченного движения записывается как 1/2 rv2, тогда как кинетическая энергия случайных (неупорядоченных) движений равна rcpT, где cp - удельная теплоемкость при постоянном давлении и T - абсолютная температура воздуха. Согласно закону сохранения энергии для установившихся течений, сумма отнесенных к единице объема энергиий упорядоченного и случайного движений сохраняет постоянное значение: срT + 1/2 v2 = const. Из этого уравнения энергии видно, что если скорость течения v увеличивается, то его температура T уменьшается. Параметры течения и движущегося тела. Силу, действующую на движущееся тело, можно выразить с помощью некоторого безразмерного параметра. Этот параметр получается, если силу отнести к некоторой комбинации существенных характеристик среды и течения, также имеющей размерность силы. По второму закону Ньютона сила F равна произведению массы на ускорение и имеет размерность ml/t 2, где m - масса, выраженная в кг, l - длина и t - время (с). Величиной, имеющей размерность силы, является произведение плотности r, квадрата скорости движения тела в среде v2 и площади S. Искомый безразмерный параметр, который называется коэффициентом силы, определяется следующим соотношением:
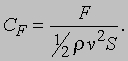
Множитель 1/2 вводится из соображений удобства, так как такой же множитель содержится в уравнении Бернулли, приведенном выше. Сила как векторная величина, характеризуется своими компонентами, имеющими различные направления. Соответственно этому различают три коэффициента сил: коэффициент подъемной силы (нормальной к скорости набегающего потока), коэффициент силы сопротивления (направленной вдоль скорости набегающего потока) и коэффициент боковой силы (ортогональной двум предыдущим). Сам коэффициент силы зависит от других безразмерных параметров. Одним из них является число Рейнольдса Re, введенное английским инженером Осборном Рейнольдсом (1842-1912). Этот критерий определяется формулой
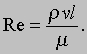
Здесь m - коэффициент вязкости, имеющий размерность m/lt. Длина l, входящая в определение критерия Рейнольдса, является характерным масштабом течения. Для течения около сферы в качестве l можно взять диаметр сферы, для самолета это хорда крыла, а для трубы - ее диаметр. Это означает, что можно сравнивать числа Рейнольдса для течений различных сред (с различными значениями r и m) около двух сфер или двух геометрически подобных самолетов. Однако не имеет смысла сравнивать числа Рейнольдса течений около сферы и около самолета, так как эти тела не являются геометрически подобными и нельзя определить один масштаб длины, устанавливающий соответствие между этими двумя видами течений. Сопоставление чисел Рейнольдса для течений около двух сфер может служить указанием об относительном влиянии вязкости среды на характер течения. Вторым определяющим критерием является число Маха M, M = v/a, введенное австрийским физиком Эрнстом Махом (1838-1916). Число Маха может служить мерой влияния сжимаемости на аэродинамические характеристики тел. Излагаемые здесь сведения касаются главным образом влияния чисел Рейнольдса и Маха на аэродинамические характеристики, т.е. на подъемную силу и сопротивление крыльев и других элементов самолета. Ниже будет показано, что каждое из этих чисел определяет некоторые особенности обтекания, соответствующие высоким или низким значениям размера тела, скорости или высоты полета.
НЕСЖИМАЕМЫЕ ТЕЧЕНИЯ
Подъемная сила. Когда крыло обтекает поток, движущийся с числом Маха, значительно меньшим единицы (т.е. скорость течения значительно меньше скорости звука), то распределения давлений по его верхней и нижней поверхностям имеют вид, показанный на рис. 3. Приведенные там же линии тока характеризуют траектории элементарных частиц текущей среды, скорости которых связаны с давлением уравнением Бернулли. Возникновение областей пониженного и повышенного давления означает, что скорость течения на верхней поверхности больше, чем на нижней. Так как давление на нижней поверхности соответственно больше, то на крыло действует сила, направленная вверх, или подъемная сила. При постоянном значении числа Рейнольдса подъемная сила Y пропорциональна плотности воздуха r, квадрату скорости полета v2, площади крыла S и углу атаки a между хордой крыла и направлением движения. Эта зависимость записывается в виде Y = 1/2 rv2Ska, где k - коэффициент пропорциональности. Разделив обе стороны этого соотношения на 1/2 rv2S, получим выражение для безразмерного коэффициента подъемной силы
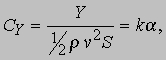
т.е. CY пропорционален углу атаки.
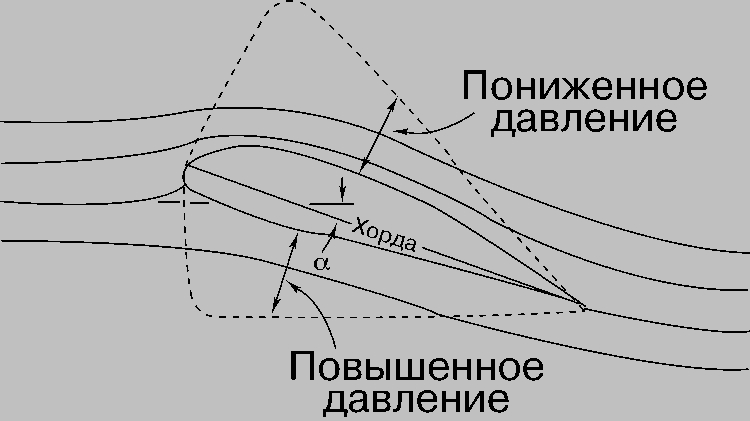
Рис. 3. ПОДЪЕМНАЯ СИЛА КРЫЛА образуется при обтекании воздухом поверхности крыла, создающего показанные пунктиром распределения давления: на верхней поверхности давление уменьшается вследствие увеличения скорости течения, а на нижней поверхности - увеличивается, толкая крыло вверх.
Коэффициент пропорциональности k принимает различные значения для крыльев различной формы в плане (рис. 4), и его величина зависит также от удлинения крыла l, определяемого соотношением l = b2/S, т.е. от отношения квадрата размаха крыла b2 к площади его поверхности S. Согласно теории, разработанной немецким ученым Людвигом Прандтлем (1875-1953),
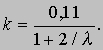
При углах атаки, меньших чем 12°, истинное значение k приблизительно на 10% меньше значения, определяемого по этой формуле.
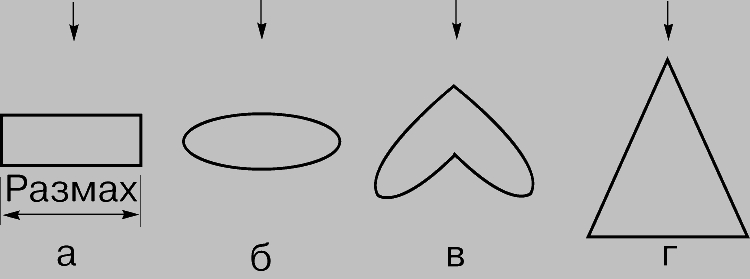
Рис. 4. ФОРМЫ КРЫЛА В ПЛАНЕ - возможные формы крыла (вид сверху). а - прямоугольное крыло; б - эллиптическое крыло; в - стреловидное крыло; г - треугольное крыло.
Влияние удлинения на величину коэффициента k и, следовательно, на подъемную силу крыла называется концевым эффектом. На рис. 5 приведен вид крыла сзади. Вследствие разности давлений происходит перетекание воздуха с нижней поверхности на верхнюю около конца крыла. Это круговое движение воздуха сохраняется позади крыла, и оно порождает концевые вихри, показанные на рис. 5,б.
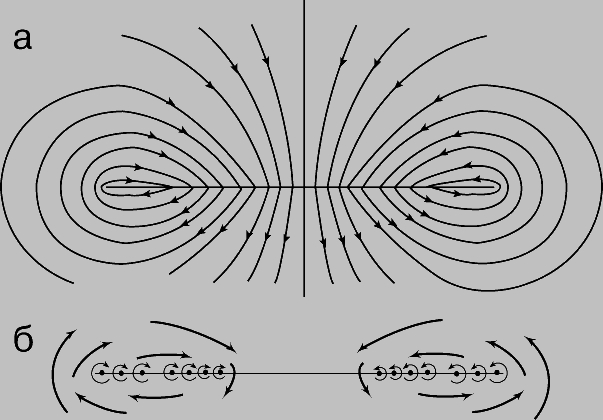
Рис. 5. ОБТЕКАНИЕ КРЫЛА (вид сзади). а - крыло, изображенное прямолинейным отрезком, окружено линиями тока, иллюстрирующими перетекание воздуха из области повышенного давления на нижней поверхности в область пониженного давления на верхней поверхности; б - вихри, образующиеся около концов крыла. Эти концевые вихри вызывают некоторое уменьшение эффективности крыла как несущей поверхности. Снижение эффективности, отражаемое уменьшением коэффициента k в соответствии с приведенным выше выражением, тем больше, чем меньше удлинение крыла.
На образование концевых вихрей расходуется некоторая часть мощности, необходимой для осуществления полета, и, следовательно, должна появляться сила сопротивления, обусловленная подъемной силой, которая называется индуктивным сопротивлением Xi. Согласно теории крыла Прандтля,
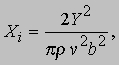
или
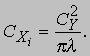
Наличие в знаменателе формулы для Xi величины b2 имеет важное значение при проектировании самолета: при заданных весе и скорости полета самолета индуктивное сопротивление в установившемся полете (когда вес уравновешивается подъемной силой) существенно уменьшается при увеличении размаха крыла. Эти соотношения выполняются строго только для крыла эллиптической формы в плане (рис. 4), однако они пригодны для приближенной оценки аэродинамических характеристик прямоугольных крыльев с удлинениями свыше трех. Прежде чем обсуждать другие ограничения, касающиеся применимости этих формул, необходимо понять происхождение вязкого сопротивления и влияния вязкости на подъемную силу крыла.
Влияние вязкости. Выше был определен коэффициент вязкости и отмечалось, что вязкая среда характеризуется свойством прилипания к твердой поверхности. Вследствие этого на поверхности тела, движущегося в вязкой среде, образуется пограничный слой, в котором скорость изменяется от скорости движения поверхности тела до скорости свободного течения на внешней границе пограничного слоя. Пограничный слой схематически изображен на рис. 6. В настоящее время исследования пограничного слоя базируются на результатах основополагающих работ Прандтля и Теодора фон Кармана (1881-1963).
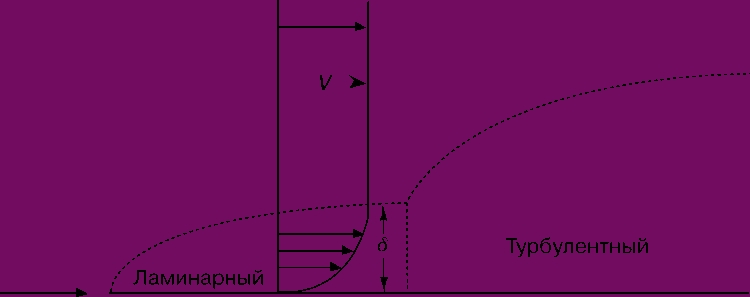
Рис. 6. ПОГРАНИЧНЫЙ СЛОЙ на плоской пластине (изображенной горизонтальной линией). Вблизи передней кромки пластины течение ламинарное (слоистое). За точкой перехода (соответствует вертикальной штриховой линии) течение турбулизуется. Одна из важных проблем аэродинамики - определение положения точки перехода, которое зависит от характеристик шероховатости поверхности, толщины и формы тела, а также от турбулентности внешнего течения и ряда других факторов.
Рисунок 6 показывает, что течение в пограничном слое слоистое (ламинарное) вблизи точки его зарождения (около передней кромки тела), но постепенно завихряется (становится турбулентным) ниже по течению. Одной из важных проблем аэродинамики является определение положения точки перехода от ламинарного течения к турбулентному. Турбулентный пограничный слой намного толще ламинарного, и их толщины зависят от числа Рейнольдса Re, определяемого как произведение величины rv/m на расстояние от передней кромки x. Толщина пограничного слоя d дается следующими соотношениями:
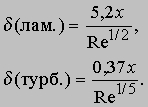
Так, на расстоянии x = 1 м от передней кромки при v = 10 м/с, r = 1,23 кг/м3, m = 1,73 x 10-5 кг/мЧс толщина ламинарного пограничного слоя составляет 0,62 x 10-2 м, а толщина турбулентного пограничного слоя - 2,5 x 10-2 м. Таким образом, турбулентный пограничный слой в четыре раза толще ламинарного; тем не менее в обоих случаях эти толщины относительно малы. Чтобы ускорить воздух в пограничном слое, к нему нужно приложить некоторую силу, и реакция на эту силу является силой сопротивления, которая называется сопротивлением трения. Коэффициенты сопротивления трения для ламинарного и турбулентного пограничных слоев даются формулами
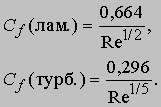
Если при условиях, указанных выше, вычислить силу трения, действующую на единицу площади, то окажется, что турбулентное трение в 25 раз больше ламинарного. Следовательно, для уменьшения силы сопротивления трения, действующей на самолет, необходимо сохранять ламинарный режим течения в пограничном слое. Кроме сопротивления трения, существует еще сопротивление формы, действующее на тело, помещенное в поток. Возникновение силы сопротивления этого типа разъясняется на рис. 7, который показывает, что среднее давление на фронтальной части поверхности летательного аппарата выше, чем в набегающем потоке, а на теневой части поверхности оно меньше давления в набегающем потоке. Суммируя все силы давления, получим сопротивление формы, которое для плохо обтекаемого тела, такого, как показанный на рис. 7 цилиндр, в сотни раз превышает сопротивление трения. Напротив, для хорошо обтекаемого тела, такого, как крыло при малых углах атаки, сопротивление формы меньше, чем сопротивление трения.
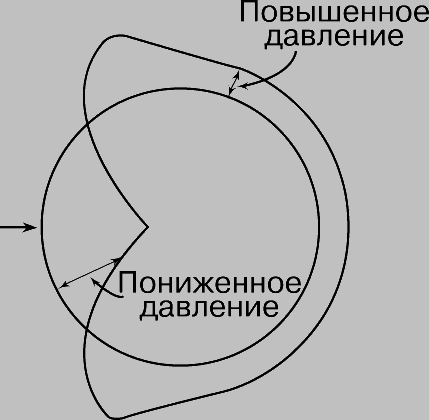
Рис. 7. СОПРОТИВЛЕНИЕ ФОРМЫ цилиндра в сотни раз выше, чем у хорошо обтекаемого тела, вытянутого вдоль линий тока. Среда, движущаяся в направлении, указанном стрелкой (слева направо), создает повышенное давление на поверхности тела, обращенной к набегающему потоку. На тыльной части тела создается пониженное давление.
Когда угол атаки крыла превышает некоторое критическое значение (заключенное в диапазоне от 12 до 15°), поток отрывается от верхней поверхности; происходит срыв потока с крыла. Он сопровождается резким падением подъемной силы и ростом сопротивления крыла. На рис. 8,а,б показаны картины линий тока около крыла до и после срыва потока. При малых углах атаки с увеличением этого угла коэффициент подъемной силы возрастает, а затем, вследствие срыва потока, проходит через максимум и резко уменьшается.
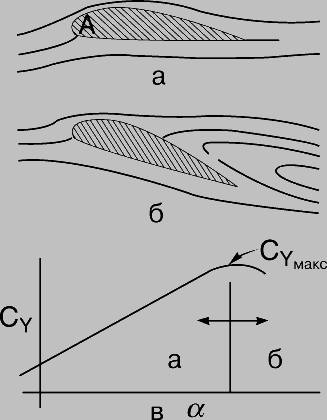
Рис. 8. СРЫВ ПОТОКА на крыле. Линии тока при безотрывном обтекании крыла (а) непрерывно огибают как нижнюю, так и верхнюю поверхности крыла, создавая подъемную силу. Если угол атаки крыла становится слишком большим, то течение отрывается от верхней поверхности (б) и подъемная сила резко уменьшается (в). а - безотрывное обтекание; б - срыв потока; в - CYMAX.
Самолет совершает посадку при большом угле атаки, при котором коэффициент подъемной силы близок к максимальному значению. Чем больше этот максимум, тем меньше посадочная скорость, и по этой причине на самолете используются различные специальные устройства для увеличения максимальной подъемной силы (средства механизации крыла). Чтобы "затянуть" срыв на более высокие углы атаки и, следовательно, увеличить максимальную подъемную силу, используют предкрылки, закрылки и отсос воздуха из пограничного слоя через поверхность (рис. 9).
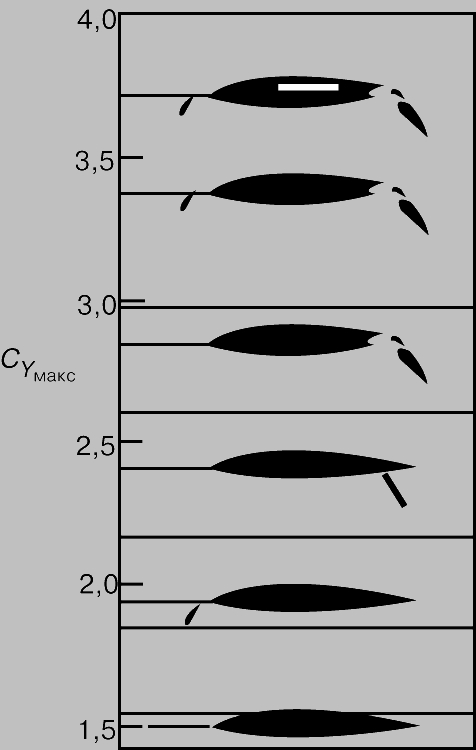
Рис. 9. КРЫЛЬЯ и различные устройства для увеличения подъемной силы (средства механизации крыла), расположенные в порядке возрастания (снизу вверх) коэффициента максимальной подъемной силы CYMAX : крыло без механизации; крыло с предкрылком; крыло с закрылком; крыло с двухщелевым закрылком; крыло с предкрылком и двухщелевым закрылком; крыло с предкрылком, двухщелевым закрылком и отсосом воздуха с верхней поверхности. Последний вариант создает наибольшую подъемную силу при больших углах атаки, которые используются при посадке самолета.
СЖИМАЕМЫЕ ТЕЧЕНИЯ
Если скорость движения тела (или воздуха относительно неподвижного тела) становится сравнимой со скоростью звука, то плотность воздуха в течении изменяется, и в коэффициентах аэродинамических сил проявляется влияние сжимаемости. Это влияние можно охарактеризовать с помощью числа Маха. Рассмотрим сначала тонкое тело с заостренным носком, такое, как игла или лезвие бритвы, при нулевом угле атаки. Создаваемые носком такого тела возмущения давления малы, и эти возмущения распространяются во все стороны от носка со скоростью звука a, равной 340 м/с при стандартной температуре 288 К (15° С). Рассмотрим два режима полета и две волновые диаграммы, иллюстрирующие распространение возмущений (волн) давления. Диаграмма рис. 10,а соответствует дозвуковому полету (с M < 1), а рис. 10,б - сверхзвуковому полету (с M > 1). Тело, движущееся со скоростью v, проходит расстояние AB за время t, так что AB = vt. За это же время волна проходит расстояние at и уходит вперед относительно тела в случае дозвукового полета. При сверхзвуковом полете волна отстает от тела, и ее фронт, касательный к окружностям распространения возмущений, образует угол b с направлением движения тела. Так как угол ACB прямой, то
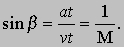
Можно видеть, что все возмущения давления образуют волновой фронт, наклоненный под углом b, который тем меньше, чем больше число Маха. Волны, генерируемые заостренными тонкими телами, называются волнами Маха, в отличие от ударных волн, рассматриваемых ниже, и угол b называется углом Маха.
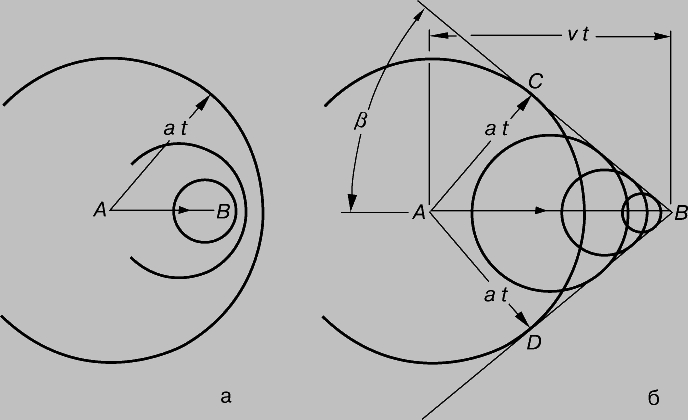
Рис. 10. ВОЛНОВЫЕ СТРУКТУРЫ, генерируемые тонким заостренным телом, перемещающимся из точки A в точку B с дозвуковой (а) или сверхзвуковой (б) скоростью. При дозвуковой скорости полета возмущения давления, распространяющиеся со скоростью звука в виде круговых волн, движутся перед телом. При сверхзвуковой скорости полета тело движется быстрее, чем волны. Фронты волны изображаются линиями BC и BD, касательными к круговым волнам.
Существуют волны давления двух типов: волны сжатия и волны разрежения. При переходе через волну сжатия происходит сжатие воздуха, и, следовательно, его плотность и давление увеличиваются. Обратная картина наблюдается в волне разрежения, при прохождении через которую имеет место разрежение воздуха, приводящее к уменьшению плотности и давления. Математический анализ уравнений течения показывает, что если образуется некоторая совокупность следующих друг за другом волн сжатия, то происходит усиление головной волны, так как последующие волны догоняют ее и сливаются с ней. Образующаяся при этом интенсивная волна называется ударной, и ее свойства отличаются от свойств более слабых волн Маха. Так, последовательность волн разрежения не улавливается головной волной, и, следовательно, ударная волна всегда является волной сжатия. Напомним, что до сих пор рассматривалось тонкое заостренное тело; затупленное тело большой толщины при сверхзвуковой скорости движения порождает сильные возмущения, т.е. ударные волны, а не волны Маха. Ударная волна движется со скоростью, превышающей скорость звука, и чем больше интенсивность волны (т.е. чем больше изменения плотности и давления в ней), тем быстрее она движется. (Например, ударная волна, возникающая при взрыве атомной бомбы, в начале своего пути перемещается со скоростью, составляющей несколько миллионов километров в час.) Угол между фронтом ударной волны и направлением течения больше угла Маха, так как скорость перемещения этой волны больше скорости звука a. Следующий пример дает количественное представление об образовании ударных волн и волн Маха. При M = 2 волна, генерируемая телом клиновидной формы (рис. 11), имеет характеристики, сходные с характеристиками волн Маха, если угол при вершине клина меньше 8°. Если этот угол больше 8°, то образуется ударная волна. На рис. 11 также приведено распределение давления на поверхности клина. При переходе через ударную волну в вершине клина давление скачкообразно увеличивается и остается постоянным до встречи с веером волн разрежения, порождаемым обтеканием угла B. Затем оно снова принимает постоянное значение, сохраняющееся до тех пор, пока не достигается ударная волна, исходящая из точки C. Линия тока abcdef состоит из прямолинейных участков, концы которых соответствуют пересечениям с волнами, генерируемыми изломами поверхности тела. Форма этой линии тока сильно отличается от формы соответствующей линии в дозвуковом течении (рис. 8), в котором линии тока начинают искривляться еще перед телом и остаются гладкими при изменении своей формы, вызванном присутствием тела.
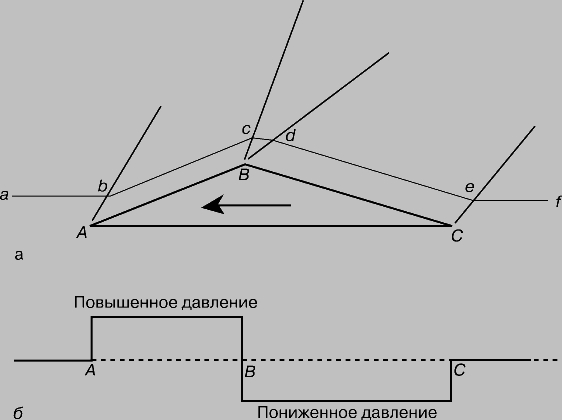
Рис. 11. КЛИНОВИДНОЕ КРЫЛО в сверхзвуковом потоке (а) и давления на участках AB и BC крыла (б).
Система волн, изображенная на рис. 11, кардинально изменяется, если угол при вершине клина превышает критическое значение, величина которого возрастает с числом Маха. При этом ударная волна, генерируемая носком тела, искривляется и отходит от тела вперед. Возникает отсоединенная ударная волна. Например, если при M = 2 угол клина больше 23°, то ударная волна будет отсоединенной. При угле клина, равном 23°, образуется присоединенная ударная волна, если M > 2, и отсоединенная, если M < 2. При M = 5 критический угол увеличивается до 41°. Аналогичные явления имеют место при обтекании тел с коническими носовыми частями, однако для конуса критический угол при фиксированном числе Маха больше, чем для клина.
Иллюстрированный энциклопедический словарь
АЭРОДИНАМИКА (от аэро... и греческого dynamis - сила), наука о законах движения газов и взаимодействии их с твердыми телами. Сложилась в 1-й четверти 20 в. в связи с потребностями развивающейся авиации в аналитическом определении подъемной силы летательного аппарата, сопротивления воздушной среды его движению, тяги воздушного винта и т.п. Различают аэродинамику внешнюю (обтекание "безграничным" потоком газа крыла самолета, лопастей воздушного винта и др.) и внутреннюю (движение газа в аэродинамических трубах, газотурбинных двигателях и др.).
Практический толковый словарь
авто обтекаемость авто
Слитно. Раздельно. Через дефис
Орфографический словарь
Словарь ударений
Формы слов для слова аэродинамика
а́эродина́мика, а́эродина́мики, а́эродина́мик, а́эродина́мике, а́эродина́микам, а́эродина́мику, а́эродина́микой, а́эродина́микою, а́эродина́миками, а́эродина́миках
Синонимы к слову аэродинамика
Морфемно-орфографический словарь
Словарь галлицизмов русского языка
АЭРОДИНАМИКА и, ж. aérodynamique f. Научная дисциплина, изучающая законы движения воздуха и других газов и их взаимодействие с движущимися в них телами. БАС-2. <Аэрометрия> разделяется на Аэростатику, Пневматику и Аэродинамику. Ян. 1 296. - Лекс. Ян. 1803: аэродинамика; Даль: аэродина/мика, аэродина/мический.