МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ - раздел молекулярной физики, рассматривающий многие свойства веществ исходя из представлений о быстром хаотическом движении огромного числа атомов и молекул, из которых эти вещества состоят. Молекулярно-кинетическая теория концентрирует внимание не на различиях между отдельными типами атомов и молекул, а на том общем, что имеется в их поведении. Еще древнегреческие философы, первыми высказывавшие атомистические идеи, полагали, что атомы находятся в непрерывном движении. Количественный анализ этого движения попытался дать Д.Бернулли в 1738. Принципиальный вклад в развитие молекулярно-кинетической теории был сделан в период с 1850 по 1900 Р.Клаузиусом в Германии, Л.Больцманом в Австрии и Дж.Максвеллом в Англии. Эти же физики заложили основы статистической механики - более абстрактной дисциплины, занимающейся изучением того же предмета, что и молекулярно-кинетическая теория, но без построения детальных, а потому менее общих моделей. Углубление статистического подхода в начале 20 в. связано главным образом с именем американского физика Дж.Гиббса, который считается одним из основоположников статистической механики. Революционные идеи были привнесены в эту науку также М.Планком и А.Эйнштейном. В середине 1920-х годов классическая механика окончательно уступила место новой, квантовой, механике. Она дала импульс развитию статистической механики, не прекращающемуся до сих пор.
МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ТЕПЛОТЫ
Известно, что нагретые тела, остывая, отдают часть своей теплоты более холодным телам. До 19 в. считалось, что теплота - это некая жидкость (теплород), перетекающая от одного тела к другому. Одним из главных достижений физики 19 в. стало то, что теплота стала рассматриваться просто как одна из форм энергии, а именно - кинетическая энергия атомов и молекул. Такое представление распространяется на все вещества - твердые, жидкие и газообразные. Частицы нагретого тела движутся быстрее, чем холодного. Например, солнечные лучи, нагревая нашу кожу, заставляют ее молекулы колебаться быстрее, и мы ощущаем эти колебания как тепло.
На холодном ветру молекулы воздуха, сталкиваясь с молекулами поверхности нашего тела, отбирают у них энергию, и мы ощущаем холод. Во всех случаях, когда тепло передается от одного тела к другому, движение частиц в первом из них замедляется, во втором ускоряется, а энергия частиц второго тела увеличивается ровно на столько, на сколько уменьшается энергия частиц первого. Многие знакомые нам тепловые явления можно непосредственно объяснить с помощью молекулярно-кинетической теории. Поскольку теплота порождается беспорядочным движением молекул, можно повышать температуру тела (увеличивать запас теплоты в нем) не за счет подвода тепла, а, например, с помощью трения: молекулы трущихся поверхностей, соударяясь друг с другом, начинают двигаться более интенсивно, и температура поверхностей повышается. По той же причине нагревается кусок железа, когда по нему бьют молотом. Еще одно тепловое явление - увеличение давления газов при нагревании. С повышением температуры скорость движения молекул увеличивается, они чаще и сильнее ударяются о стенки сосуда, в котором газ находится, что проявляется в повышении давления. Постепенное испарение жидкостей объясняется тем, что их молекулы одна за другой переходят в воздух, при этом первыми улетучиваются самые быстрые из них, а у тех, которые остаются, энергия в среднем оказывается меньше. Вот почему при испарении жидкостей с влажной поверхности она охлаждается. Математический аппарат, построенный на молекулярно-кинетической теории, позволяет анализировать эти и многие другие эффекты, исходя из уравнений движения молекул и общих положений теории вероятностей. Предположим, что мы подняли резиновый мяч на некоторую высоту, а затем выпустили его из рук. Мяч ударится об пол, а затем несколько раз подскочит, каждый раз на меньшую высоту, чем перед этим, поскольку при ударе часть его кинетической энергии превращается в теплоту. Такой удар называется частично упругим. Кусок свинца совсем не отскакивает от пола - при первом же ударе в теплоту превращается вся его кинетическая энергия, и температура куска свинца и пола слегка повышается. Такой удар называют абсолютно неупругим. Удар, при котором вся кинетическая энергия тела сохраняется, не превращаясь в тепло, называется абсолютно упругим. В газах при столкновении атомов и молекул друг с другом происходит лишь обмен их скоростями (мы не рассматриваем здесь случай, когда в результате столкновений частицы газа взаимодействуют - вступают в химические реакции); суммарная кинетическая энергия всей совокупности атомов и молекул не может при этом превратиться в теплоту, поскольку она уже ею является. Непрерывное движение атомов и молекул вещества называется тепловым движением. В жидкостях и твердых телах картина более сложная: помимо кинетической энергии необходимо учитывать и потенциальную энергию взаимодействия частиц.
Тепловое движение в воздухе. Если воздух охладить до очень низкой температуры, то он превратится в жидкость, при этом объем образовавшейся жидкости будет очень мал. Например, при ожижении 1200 см3 атмосферного воздуха получаются 2 см3 жидкого воздуха. Основное допущение атомной теории состоит в том, что размеры атомов и молекул при изменении агрегатного состояния вещества почти не изменяются. Следовательно, в атмосферном воздухе молекулы должны находиться друг от друга на расстояниях, гораздо больших, чем в жидкости. Действительно, из 1200 см3 атмосферного воздуха более 1198 см3 занимает пустое пространство. Молекулы воздуха движутся хаотически в этом пространстве с очень высокими скоростями, постоянно сталкиваясь друг с другом наподобие бильярдных шаров.
Давление газа или пара. Рассмотрим прямоугольный сосуд, в единице объема которого содержится n молекул газа массой m каждая. Нас будут интересовать только те молекулы, которые ударяются об одну из стенок сосуда. Выберем ось x так, чтобы она была перпендикулярна этой стенке и рассмотрим молекулу, у которой составляющая скорости v вдоль выбранной нами оси равна vx. При ударе молекулы о стенку сосуда ее импульс в направлении оси x изменится на величину -2mvx. В соответствии с третьим законом Ньютона таков же будет импульс, переданный стенке. Можно показать, что если все молекулы движутся с одинаковыми скоростями, то с единицей площади стенки в 1 с сталкивается (1/2) nvx молекул. Чтобы убедиться в этом, рассмотрим пограничный слой газа вблизи одной из стенок, заполненный молекулами с одинаковыми величинами v и vx (рис. 1). Предположим, что толщина этого слоя настолько мала, что большинство молекул пролетают его без столкновений. Молекула А долетит до стенки в момент времени t = l /vx ; к этому времени о стенку ударится ровно половина молекул из пограничного слоя (другая половина движется от стенки). Их число определяется плотностью газа и объемом пограничного слоя площадью А и толщиной l: N = (1/2) nAl. Тогда число молекул, ударившихся о единичную площадку за 1 с, составит N/At = (1/2) nvx, и полный импульс, переданный этой площадке за 1 с, будет равен (1/2) nvx Ч2mvx = nmvx2. На самом деле составляющая vх неодинакова для разных молекул, поэтому величину vx2 следует заменить ее средним значением
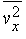
Если молекулы движутся хаотически, то среднее всех vх равно среднему для vy и vz, так что
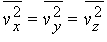
и
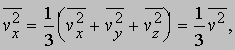
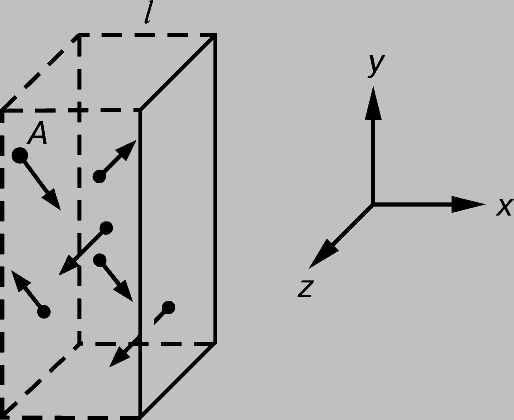
Рис. 1. ДАВЛЕНИЕ ГАЗА на стенки сосуда можно найти, рассматривая импульс, передаваемый молекулами стенкам.
где - среднее для всех молекул значение v2. Удары молекул о стенку так быстро следуют один за другим, что последовательность передаваемых импульсов воспринимается как постоянное давление Р. Величину Р можно найти, если вспомнить, что давление - это сила, действующая на единицу площади, а сила, в свою очередь, - это скорость изменения импульса. Следовательно, Р равно скорости изменения импульса, приходящегося на единицу площади, т.е.
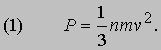
Такое же соотношение мы получим, если вместо случайного движения молекул во всех направлениях будем рассматривать движение одной шестой их числа перпендикулярно каждой из шести граней прямоугольного сосуда, считая, что каждая молекула обладает кинетической энергией
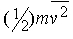
.
Закон Бойля - Мариотта. В формуле (1) через n обозначено не полное число молекул, а число молекул в единице объема. Если то же число молекул поместить в половину объема (не изменив при этом температуру), то величина n удвоится, при этом удвоится и давление, если v2 не зависит от плотности. Иначе говоря, при постоянной температуре давление газа обратно пропорционально объему. Английский физик Р. Бойль и французский физик Э. Мариотт экспериментально установили, что при низких давлениях это утверждение справедливо для любого газа. Таким образом, закон Бойля - Мариотта можно объяснить, сделав разумное предположение, что при низких давлениях скорость молекул не зависит от n.
Закон Дальтона. Если в сосуде находится смесь газов, т.е. имеются несколько разных сортов молекул, то импульс, передаваемый стенке молекулами каждого сорта, не зависит от того, присутствуют ли молекулы других сортов. Таким образом, согласно молекулярно-кинетической теории, давление смеси двух или большего числа идеальных газов равно сумме давлений, которые создавал бы каждый из газов, если бы занимал весь объем. В этом и состоит закон Дальтона, которому подчиняются газовые смеси при низких давлениях.
Скорости молекул. Формула (1) позволяет оценить среднюю скорость молекул газа. Так, атмосферное давление на уровне моря составляет примерно 106 дин/см2 (0,1 МПа), а масса 1 см3 воздуха равна 0,0013 г. Подставив эти значения в формулу (1), мы получим для скорости молекул очень большую величину:
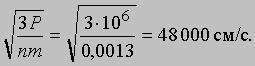
На большой высоте над уровнем моря, где атмосфера очень разрежена, молекулы воздуха за секунду могут перемещаться на огромные расстояния, не сталкиваясь друг с другом. У поверхности Земли наблюдается иная картина: за 1 с каждая молекула сталкивается с другими молекулами в среднем ок. 800 миллионов раз. Она описывает в высшей степени изломанную траекторию, и в отсутствие воздушных потоков через одну секунду с высокой вероятностью оказывается на расстоянии всего 1-2 см от того места, где она находилась в начале этой секунды.
Закон Авогадро. Как мы уже говорили, воздух при комнатной температуре имеет плотность примерно 0,0013 г/см3 и создает давление МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ106 дин/см2. Газообразный водород, плотность которого при комнатной температуре равна всего лишь 0,00008 г/см3, тоже создает давление в 106 дин/см2. Согласно формуле (1), давление газа пропорционально числу молекул в единице объема и их средней кинетической энергии. В 1811 итальянский физик А.Авогадро выдвинул гипотезу, согласно которой равные объемы различных газов при одинаковых температуре и давлении содержат одинаковое число молекул. Если эта гипотеза верна, то из соотношения (1) получим, что для разных газов при указанных выше условиях величина (1/2) mv2 одинакова, т.е. одинакова средняя кинетическая энергия молекул. Этот вывод вполне согласуется с молекулярно-кинетической теорией
(см. также ТЕПЛОТА).
Масса 1 см3 водорода мала не потому, что в данном объеме присутствует меньше молекул, а потому, что масса каждой молекулы водорода в несколько раз меньше массы молекулы азота или кислорода - газов, из которых в основном состоит воздух. Установлено, что число молекул любого газа в 1 см3 при 0° С и нормальном атмосферном давлении равно 2,687*10 19.
Средняя длина свободного пробега. Важной величиной в молекулярно-кинетической теории газов является среднее расстояние, пробегаемое молекулой между двумя столкновениями. Эта величина называется средней длиной свободного пробега и обозначается через L. Вычислить ее можно следующим образом. Представим себе, что молекулы - это сферы радиусом r ; тогда их центры при столкновении будут находиться на расстоянии 2r друг от друга. При своем движении молекула "задевает" все молекулы в пределах поперечного сечения площадью p (2r)2 и, перемещаясь на расстояние L, она "заденет" все молекулы в объеме 4pr2L, так что среднее число молекул, с которыми она столкнется, будет равно 4pr2Ln. Чтобы найти L, нужно принять это число равным 1, откуда
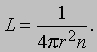
Из этого соотношения можно прямо найти радиус молекулы, если известна величина L (ее можно найти из измерений вязкости газа; см. ниже). Величина r оказывается порядка 10-8 см, что согласуется с результатами других измерений, а L для типичных газов при обычных условиях составляет от 100 до 200 диаметров молекул. В таблице приведены значения L для атмосферного воздуха на разной высоте над уровнем моря.
РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ПО СКОРОСТЯМ
В середине 19 в. происходило не только развитие молекулярно-кинетической теории, но и становление термодинамики. Некоторые понятия термодинамики оказались полезными и для молекулярно-кинетической теории - это в первую очередь абсолютная температура и энтропия.
Тепловое равновесие. В термодинамике свойства веществ рассматриваются в основном исходя из представления о том, что любая система стремится к состоянию с наибольшей энтропией и, достигнув такого состояния, не может самопроизвольно выйти из него. Такое представление согласуется с молекулярно-кинетическим описанием поведения газа. Совокупность молекул газа обладает некоторой суммарной энергией, которая может быть распределена между отдельными молекулами огромным числом способов. Каким бы ни было начальное распределение энергии, если газ предоставить самому себе, то энергия быстро перераспределится и газ придет в состояние теплового равновесия, т.е. в состояние с наибольшей энтропией. Попытаемся сформулировать это утверждение более строго. Пусть N (E) dЕ - это число молекул газа с кинетической энергией в интервале от E до Е + dE. Независимо от начального распределения энергии газ, предоставленный сам себе, придет в состояние теплового равновесия с характерной функцией N (E), соответствующей установившейся температуре. Вместо энергий можно рассматривать скорости молекул. Обозначим через f (v) dv число молекул со скоростями, лежащими в интервале от v до v + dv. В газе всегда найдется некоторое число молекул со скоростями в интервале от v до v + dv. Уже мгновение спустя ни одна из этих молекул не будет обладать скоростью, лежащей в указанном интервале, поскольку все они претерпят одно или несколько столкновений. Но зато другие молекулы со скоростями, ранее значительно отличавшимися от v, в результате столкновений приобретут скорости, лежащие в интервале от v до v + dv. Если газ находится в стационарном состоянии, то число молекул, которые приобретут скорость v, через достаточно большой промежуток времени будет равно числу молекул, скорость которых перестанет быть равной v. Только в этом случае функция n (v) может оставаться постоянной. Это число, разумеется, зависит от распределения молекул газа по скоростям. Форму этого распределения в покоящемся газе установил Максвелл: если всего имеется N молекул, то число молекул со скоростями в интервале от v до v + dv равно
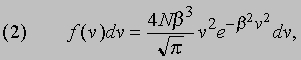
где параметр b зависит от температуры (см. ниже).
Газовые законы. Приведенные выше оценки для средней скорости молекул воздуха на уровне моря соответствовали обычной температуре. Согласно молекулярно-кинетической теории, кинетическая энергия всех молекул газа и есть та теплота, которой он обладает. При более высокой температуре молекулы движутся быстрее и газ содержит больше теплоты. Как следует из формулы (1), если объем газа постоянен, то с ростом температуры его давление повышается. Именно так ведут себя все газы (закон Шарля). Если же газ нагревать при постоянном давлении, то он будет расширяться. Установлено, что при низком давлении для любого газа объемом V, содержащим N молекул, произведение давления на объем пропорционально абсолютной температуре:
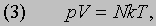
где T - абсолютная температура, k - константа. Из закона Авогадро следует, что величина k одинакова для всех газов. Она называется постоянной Больцмана и равна 1,38*10 -14 эрг/К. Сравнив выражения (1) и (3), нетрудно заметить, что полная энергия поступательного движения N молекул, равная (1/2) Nmv2, пропорциональна абсолютной температуре и равна
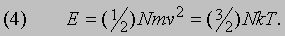
С другой стороны, проинтегрировав выражение (2), получим, что полная энергия поступательного движения N молекул равна 3Nm /4b 2. Отсюда
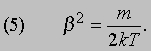
Подставив выражение (5) в формулу (2), можно найти распределение молекул по скоростям при любой температуре T. Молекулы многих распространенных газов, например азота и кислорода (основных компонентов атмосферного воздуха), состоят из двух атомов, а их молекула напоминает по форме гантель. Каждая такая молекула не только движется поступательно с огромной скоростью, но и очень быстро вращается. Помимо энергии поступательного движения, N молекул обладают энергией вращательного движения NkT, так что полная энергия N молекул равна (5/2) NkT.
Экспериментальная проверка распределения Максвелла. В 1929 появилась возможность непосредственно находить распределение молекул газа по скоростям. Если в стенке сосуда, содержащего газ или пар при определенной температуре, проделать маленькое отверстие или прорезать узкую щель, то молекулы будут вылетать через них наружу, каждая со своей скоростью. Если отверстие ведет в другой сосуд, из которого откачан воздух, то большинство молекул до первого столкновения успеют пролететь расстояние в несколько сантиметров. В установке, схематически изображенной на рис. 2, имеется сосуд V, содержащий газ или пар, молекулы которого вылетают через щель S1; S2 и S3 - щели в поперечных пластинах; W1 и W2 - два диска, насаженных на общий вал R. В каждом диске прорезано несколько радиальных щелей. Щель S3 расположена так, что, если бы не было дисков, вылетевшие из щели S1 и прошедшие сквозь щель S2 молекулы пролетали бы и сквозь щель S3 и попадали на детектор D. Если одна из щелей диска W1 окажется напротив щели S2, то молекулы, пролетевшие сквозь щели S1 и S2, пройдут и сквозь щель диска W1, но их задержит диск W2, насаженный на вал R так, что его щели не совпадают со щелями диска W1. Если диски неподвижны или медленно вращаются, то молекулы из сосуда V не попадают в детектор D. Если же диски быстро вращаются с постоянной скоростью, то некоторые из молекул проходят сквозь оба диска. Нетрудно понять, какие молекулы смогут преодолеть оба препятствия, - те, которые преодолеют расстояние от W1 до W2 за время, необходимое для смещения щели диска W2 на нужный угол. Например, если все щели диска W2 повернуты на угол 2° относительно щелей диска W1, то в детектор попадут молекулы, которые пролетают от W1 до W2 за время поворота диска W2 на 2°. Изменяя частоту вращения вала с дисками, можно измерять скорости молекул, вылетающих из сосуда V, и построить их распределение. Полученное таким образом распределение хорошо согласуется с максвелловским.
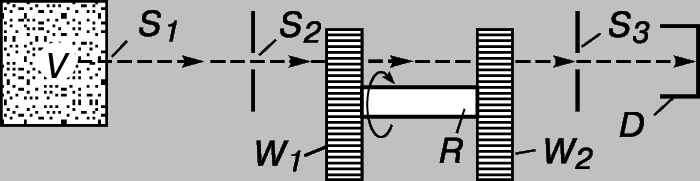
Рис. 2. СХЕМА УСТАНОВКИ для исследования распределения молекул газа по скоростям.
Броуновское движение. В 19 в. метод измерения скоростей молекул, описанный выше, еще не был известен, но одно явление позволяло наблюдать непрестанное тепловое движение молекул в жидкости. Шотландский ботаник Р.Браун (в прежней транскрипции - Броун) в 1827, наблюдая под микроскопом за частицами цветочной пыльцы, взвешенными в воде, обнаружил, что они не стоят на месте, а все время движутся, словно что-то толкает их то в одну, то в другую сторону. Позднее было высказано предположение, что хаотическое движение частиц вызвано непрерывным тепловым движением молекул жидкости, а точные исследования движения, получившего название броуновского, подтвердили правильность этой гипотезы
(см. БРОУНОВСКОЕ ДВИЖЕНИЕ).
Теплоемкость газа или пара. Количество теплоты, необходимое для повышения температуры некоторого количества вещества на 1 градус, называется его теплоемкостью. Из формулы (4) следует, что если температуру газа повысить при постоянном объеме от T до T + 1, то энергия поступательного движения увеличится на (3/2) Nk. Вся тепловая энергия одноатомного газа есть энергия поступательного движения. Следовательно, теплоемкость такого газа при постоянном объеме Cv = (3/2) Nk, а теплоемкость на одну молекулу составляет (3/2) k. Теплоемкость N двухатомных молекул, обладающих еще и энергией вращательного движения kT, равна Cv = (5/2) Nk, а на одну молекулу приходится (5/2) k. В обоих случаях теплоемкость не зависит от температуры, а тепловая энергия дается выражением
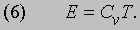
Давление насыщенного пара. Если налить немного воды в большой закрытый сосуд, в котором есть воздух, но отсутствуют водяные пары, то некоторое ее количество немедленно испарится и частички пара начнут распространяться по всему сосуду. Если объем сосуда очень велик по сравнению с объемом воды, то испарение будет идти до тех пор, пока вся вода не превратится в пар. Если же воды налито достаточно много, то испарится не вся она; скорость испарения будет постепенно уменьшаться и в конце концов процесс остановится - произойдет насыщение объема сосуда водяными парами. С позиций молекулярно-кинетической теории это объясняется следующим образом. Время от времени та или иная молекула воды, находящаяся в жидкой среде вблизи поверхности, получает от соседних молекул достаточно энергии, чтобы вырваться в паровоздушную среду. Здесь она сталкивается с другими такими же молекулами и с молекулами воздуха, описывая весьма замысловатую зигзагообразную траекторию. В своем движении она также ударяется о стенки сосуда и о поверхность воды; при этом она может отскочить от воды или поглотиться ею. Пока вода испаряется, число молекул пара, захватываемых ею из паровоздушной среды, остается меньше числа молекул, покидающих воду. Но наступает момент, когда эти величины уравниваются - устанавливается равновесие, и давление пара достигает насыщения. В таком состоянии число молекул в единице объема пара над жидкостью остается постоянным (конечно, если постоянна температура). Такая же картина наблюдается и для твердых тел, но для большинства тел давление пара становится ощутимым только при высоких температурах.
КОЛЕБАНИЯ АТОМОВ В ТВЕРДЫХ ТЕЛАХ И ЖИДКОСТЯХ
Рассматривая под микроскопом хорошо сохранившуюся древнегреческую или древнеримскую гемму, можно увидеть, что ее детали остались такими же четкими, какими они, по-видимому, были, когда гемма только что вышла из рук изготовившего ее мастера. Ясно, что за огромное время лишь очень немногие атомы смогли "вырваться" с поверхности камня, из которого сделана гемма, - в противном случае ее детали со временем потеряли бы четкость. Большинство атомов твердого тела могут совершать только колебательные движения относительно некоторого фиксированного положения, и с повышением температуры лишь увеличиваются средняя частота этих колебаний и их амплитуда. Когда вещество начинает плавиться, поведение его молекул становится похожим на поведение молекул жидкости. Если в твердом теле каждая частица колеблется в небольшом объеме, занимающем в пространстве фиксированное положение, то в жидкости и сам этот объем медленно и беспорядочно перемещается, а вместе с ним перемещается и колеблющаяся частица.
ТЕПЛОПРОВОДНОСТЬ ГАЗА
В любом неравномерно нагретом теле теплота передается от более теплых его частей к более холодным. Это явление называется теплопроводностью. Используя молекулярно-кинетическую теорию, можно найти скорость, с которой газ проводит тепло. Рассмотрим газ, заключенный в прямоугольный сосуд, верхняя поверхность которого имеет более высокую температуру, чем нижняя. Температура газа в сосуде постепенно понижается при переходе от верхних слоев к нижним - в газе существует температурный градиент. Рассмотрим тонкий горизонтальный слой газа АВ, имеющий температуру Т (рис. 3), и соседний слой CD с несколько более высокой температурой, T ў. Пусть расстояние между АВ и CD равно средней длине свободного пробега L. Согласно формуле (4), средняя энергия молекулы в слое АВ пропорциональна температуре Т, а в слое CD - температуре T'. Рассмотрим молекулу из слоя АВ, которая сталкивается с другой молекулой в точке А, после чего движется без столкновений до точки С; с большой вероятностью она попадет в слой CD с энергией, соответствующей слою АВ. И наоборот, молекула из слоя CD, движущаяся без столкновений из точки D в точку В, с большой вероятностью попадет в слой АВ с большей энергией, соответствующей слою CD, откуда она вылетела. Ясно, что при таких столкновениях от CD к АВ передается больше энергии, чем от АВ к CD, - от более теплого слоя к более холодному идет непрерывный поток тепла. Такая же картина наблюдается для всех слоев в газе.
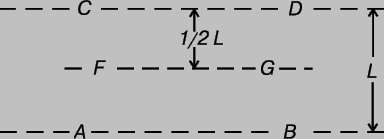
Рис. 3. АНАЛИЗ ПОВЕДЕНИЯ МОЛЕКУЛ в соседних слоях жидкости или газа при наличии градиента температуры или скорости.
Скорость распространения тепла можно вычислить с достаточно хорошей точностью, даже если пренебречь тем, что длина свободного пробега одних молекул больше, а других - меньше средней. Рассмотрим плоскость FG, параллельную плоскостям АВ и CD и проходящую посредине между ними (рис. 3), и выделим единичную площадку этой плоскости. Если в единице объема имеется n молекул, движущихся со средней скоростью с, то за 1 с (1/2) nc молекул пересекут FG снизу вверх и перенесут энергию (1/2) ncE ; такое же число молекул пересечет FG сверху вниз и перенесет энергию (1/2) ncEў, где E и Еў - средние энергии молекул при температурах Т и Т'. Таким образом, если бы оба потока молекул двигались перпендикулярно плоскости FG, то разность перенесенных энергий была бы равна (1/2) nc (Е' - Е). Но молекулы пересекают FG под всевозможными углами, и, чтобы учесть это, указанную величину следует умножить на 2/3. Используя соотношение (6), получим
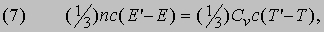
где Cv - теплоемкость n молекул, содержащихся в единице объема. При переходе от CD к АВ, находящихся друг от друга на расстоянии L, температура понижается на (Т' - Т) и если dT/dz - градиент температуры в направлении, перпендикулярном плоскости FG, то
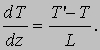
Подставляя разность температур, выраженную через градиент, в формулу (7), получаем, что полная энергия, переносимая через единичную площадку за 1 с, равна
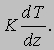
Величина K, описываемая выражением K = (1/3)CvcL,
называется коэффициентом теплопроводности газа.
ВЯЗКОСТЬ ГАЗА
Если измерять скорость течения реки на разной глубине, то можно обнаружить, что у дна вода почти неподвижна, а чем ближе к поверхности, тем быстрее она движется. Таким образом, в речном потоке имеется градиент скорости, аналогичный рассмотренному выше градиенту температуры; при этом благодаря вязкости каждый выше расположенный слой увлекает за собой соседний, лежащий под ним. Такая картина наблюдается не только в жидкостях, но и в газах. Используя молекулярно-кинетическую теорию, попытаемся определить вязкость газа. Предположим, что газ течет слева направо и что в горизонтальном слое CD на рис. 3 скорость течения больше, чем в слое АВ, расположенном непосредственно под CD. Пусть, как и прежде, расстояние между плоскостями равно средней длине свободного пробега. Молекулы газа быстро движутся по всему объему по хаотическим траекториям, но на это хаотическое движение накладывается направленное движение газа. Пусть u - скорость потока газа в слое АВ (в направлении от А к В), а u' - несколько большая скорость в слое CD (в направлении от C к D). Помимо импульса, обусловленного хаотическим движением, молекула в слое АВ обладает импульсом mu, а в слое CD - импульсом muў. Молекулы, переходящие без столкновений из АВ в CD, переносят в слой CD импульс mu, соответствующий слою АВ, тогда как частицы, попадающие из CD в АВ, смешиваются с молекулами из АВ и приносят с собой импульс mu'. Следовательно, из CD в АВ через единичную площадку плоскости FG за 1 с постоянно переносится импульс, равный
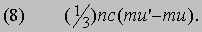
Поскольку скорость изменения импульса равна силе, мы получили выражение силы, приходящейся на единицу площади, с которой один слой действует на другой: более медленный слой тормозит более быстрый, а тот, напротив, увлекая за собой более медленный слой, ускоряет его. Аналогичные силы действуют между соседними слоями во всем объеме текущего газа. Если du/dz -градиент скорости в газе в направлении, перпендикулярном FG, то
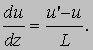
Величина nm в формуле (8) есть масса газа в единице объема; если обозначить эту величину через r, то сила, приходящаяся на единицу площади, будет равна
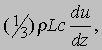
где коэффициент (1/3)rLc - вязкость газа. Из последних двух разделов статьи следуют два вывода. Первый состоит в том, что отношение вязкости к теплопроводности равно r/Cv. Второй вытекает из приведенного ранее выражения для L и состоит в том, что вязкость газа зависит только от его температуры и не зависит от давления и плотности. Правильность обоих выводов с высокой точностью подтверждена экспериментально.
См. также
ЛИТЕРАТУРА
Гиршфельд Дж., Кертисс Ч., Берд Р. Молекулярная теория газов и жидкостей. М., 1961 Френкель Я.И. Кинетическая теория жидкостей. Л., 1975 Кикоин А.К., Кикоин И.К. Молекулярная физика. М., 1976