м.
1. Раздел геофизики, изучающий распределение в пространстве и изменение во времени магнитного поля Земли и связанные с ним геофизические процессы.
2. Магнитное поле Земли.
м.
1. Раздел геофизики, изучающий распределение в пространстве и изменение во времени магнитного поля Земли и связанные с ним геофизические процессы.
2. Магнитное поле Земли.
ГЕОМАГНЕТИ́ЗМ -а; м. [от греч. gē - Земля и magnētis (lithos) - магнитный (камень)].
1. Геофиз. Область изучения распределения в пространстве и изменения во времени магнитного поля Земли и связанных с ним геофизических процессов.
2. Магнитное поле Земли.
◁ Геомагни́тный, -ая, -ое. Г-ые бури. Г-ое поле. Г-ая карта.
* * *
геомагнети́зм - 1) магнитное поле Земли; 2) раздел геофизики, в котором изучаются распределение в пространстве и изменения во времени магнитного поля Земли, а также связанные с ним геофизические процессы в Земле и её магнитосфере.
* * *
ГЕОМАГНЕТИЗМ - ГЕОМАГНЕТИ́ЗМ,
1) магнитное поле Земли (см. МАГНИТНОЕ ПОЛЕ ЗЕМЛИ) .
2) Раздел геофизики (см. ГЕОФИЗИКА), в котором изучается распределение в пространстве и изменения во времени магнитного поля Земли, а также связанные с ним геофизические процессы в Земле и ее магнитосфере (см. МАГНИТОСФЕРА) .
ГЕОМАГНЕТИЗМ - 1) магнитное поле Земли.
2) Раздел геофизики, в котором изучается распределение в пространстве и изменения во времени магнитного поля Земли, а также связанные с ним геофизические процессы в Земле и ее магнитосфере.
ГЕОМАГНЕТИЗМ - земной магнетизм, магнитное поле Земли и околоземного космического пространства. Земля обладает магнитным полем дипольного типа, как будто бы в ее центре расположен гигантский полосовой магнит. Конфигурация этого поля медленно изменяется, вероятно в результате движения расплавленного материала во внешнем ядре Земли на глубинах более 2900 км. Главное магнитное поле обусловлено источниками, расположенными в глубинах Земли. На медленные вариации главного магнитного поля накладываются быстрые, но слабые изменения, вызванные электрическими токами в ионосфере. Электрические свойства ионосферы связаны с присутствием в ней заряженных частиц, возникающих при ионизации атмосферы солнечным излучением. Ветры, дующие в ионосфере в присутствии постоянного магнитного поля Земли, приводят к возникновению электрических токов, которые, в свою очередь, создают дополнительное изменяющееся магнитное поле. Кроме этих регулярных магнитных вариаций, наблюдаются также возмущения, обусловленные происходящими время от времени солнечными вспышками - источниками ультрафиолетовых и рентгеновских лучей и возмущенного потока заряженных частиц солнечного ветра. Эта радиация увеличивает ионизацию и вызывает дополнительные электрические токи в ионосфере. Временами солнечный ветер настолько эффективно взаимодействует с геомагнитным полем, что формирует кольцевой электрический ток на расстоянии в несколько радиусов земного шара; это приводит к уменьшению главного магнитного поля; такие магнитные возмущения ощущаются во всем мире, но наиболее сильно проявляются в полярных районах. В периоды сильных магнитных возмущений происходят особенно интенсивные полярные сияния, а также часто нарушается дальняя радиосвязь. Исследования магнитного поля Земли используются для изучения физического состояния глубоких недр и процессов, происходящих в высоких слоях атмосферы. Наблюдения магнитных вариаций проводятся на земной поверхности, в океанах, а также с воздуха и из космоса с помощью самолетов и спутников. Магнитное поле играет также важную роль в областях, отстоящих от поверхности Земли на тысячи и более километров; в их пределах интенсивный поток частиц, захваченных магнитным полем, создает серьезные проблемы для аэрокосмических исследований. Солнечные и галактические космические лучи, несмотря на их высокую энергию, отклоняются магнитным полем Земли до того, как попадут в пределы атмосферы.
См. также АТМОСФЕРА.
Историческая справка. Если полосовой магнит свободно подвесить на нити, прикрепленной к его центру, ось магнита в первом приближении сориентируется в направлении север - юг. Точно не известно, когда было впервые обнаружено такое свойство магнита. Возможно, китайцы были знакомы с ним уже в 1100, однако практическое использование этого явления началось лишь 200 лет спустя. В Западной Европе магнитный компас применяется в навигации с 1187. Основы науки о геомагнетизме были заложены в период между 13 и 16 столетиями. К середине 15 в. стало известно, что подвешенный магнит не всегда указывает точно на север. Первые сведения о наклонении направления земного магнитного поля относительно горизонтальной плоскости появились в середине 16 в. В 1600 У. Гильберт, придворный врач Елизаветы I, опубликовал знаменитый трактат О магните, магнитных телах и о большом магните - Земле. Новая физиология, доказанная множеством аргументов и опытов (De magnete, magneticisque corporibus et de magno magnete tellure. Physiologia nova; рус. перевод 1956), в котором описал свойства магнита и земного магнетизма. Он отметил, что Земля, по-видимому, является огромным сферическим магнитом. Вариации магнитного поля во времени были зафиксированы в 1635 Г. Геллибрандтом, профессором астрономии Грешам-Колледжа (Лондон). В 1701 астроном Э. Галлей опубликовал первую карту геомагнитного поля. В середине 18 в. была установлена связь между полярным сиянием и магнитными вариациями. В 19 в. К. Гаусс, внесший большой вклад в развитие знаний о геомагнетизме, усовершенствовал приборы для измерения магнитных вариаций и установил их в магнитной обсерватории в Геттингене, построенной в 1833 из немагнитных материалов. В 1834 Гаусс и В.Вебер приняли участие в программе Ф.Гумбольдта наблюдений за магнитными явлениями, которую одновременно проводили ок. 50 обсерваторий, входивших в Геттингенский магнитный союз. Гаусс обобщил магнитные данные и математически доказал гипотезу Гильберта о том, что источник главного (основного) магнитного поля находится внутри Земли.
Описание геомагнитного поля. В любой точке Земли магнитное поле исчерпывающим образом характеризуется его интенсивностью и направлением, угол которого с горизонтальной плоскостью называется магнитным наклонением (I). Если спроектировать поле на горизонтальную плоскость, направление в первом приближении будет ориентировано с севера на юг, но в общем случае будет образовывать некоторый угол с истинным направлением географического меридиана; это отклонение носит название магнитного склонения (D). Амплитуда, или напряженность, магнитного поля называется полной магнитной интенсивностью (F). Магнитное поле может быть представлено двумя взаимно перпендикулярными компонентами: горизонтальной (H) и вертикальной (Z). Если векторы, показывающие интенсивность и направление горизонтальной компоненты в различных точках Земли, нанести на карту, то видно, что они расходятся от точки вблизи Южного полюса и сходятся в точке вблизи Северного полюса. Эти точки называются соответственно Южным и Северным магнитными полюсами. На полюсах магнитное поле направлено вертикально. Линию, на которой магнитное поле направлено горизонтально, называют магнитным экватором. Магнитные полюсы не совпадают с географическими и весьма быстро перемещаются. Северный магнитный полюс находится в северных водах Канады. Его координаты в 1900 были 69° с.ш. и 97° з.д., в 1950 - 72° с.ш. и 96° з.д., в 1980 - 75° с.ш. и 100° з.д, а в 1985 - 77° с.ш. и 102° з.д. Южный магнитный полюс в 1985 имел координаты 65,5° ю.ш. и 139,5° в.д. Прямая линия, проведенная через эти магнитные полюсы, не проходит через центр Земли. Измерения геомагнитного поля показывают, что на поверхности Земли в целом оно может быть представлено как поле полосового магнита, помещенного в центре планеты. Его еще называют полем магнитного диполя; вне сферы оно имеет такую конфигурацию, как если бы сфера была однородно намагничена. Эта модель дает наилучшее (но далеко не идеальное) совпадение с действительным полем. Две точки, в которых ось диполя пересекает земную поверхность, называют геомагнитными полюсами. В начале 1990-х годов геомагнитный экватор был наклонен к географическому экватору на 12°. Северный геомагнитный полюс имел координаты 79° с.ш. и 70° з.д., а ось диполя отстояла от центра Земли на 460 км в направлении Тихого океана (18° с.ш., 148° в.д.). Полная магнитная напряженность на геомагнитных полюсах равняется примерно 0,6 гаусс, на магнитном экваторе напряженность примерно вдвое меньше.
Магнитные карты. Распределение геомагнитного поля у земной поверхности может быть представлено в виде изомагнитных линий, т.е. линий, вдоль которых значение конкретной компоненты остается постоянным. Карты склонения называются картами изогон (рис. 1). Магнитные карты основаны на многочисленных магнитных съемках, выполняемых на суше, на море и с воздуха. В США магнитные карты готовятся Береговой и геодезической службой и Военно-гидрографическим управлением.
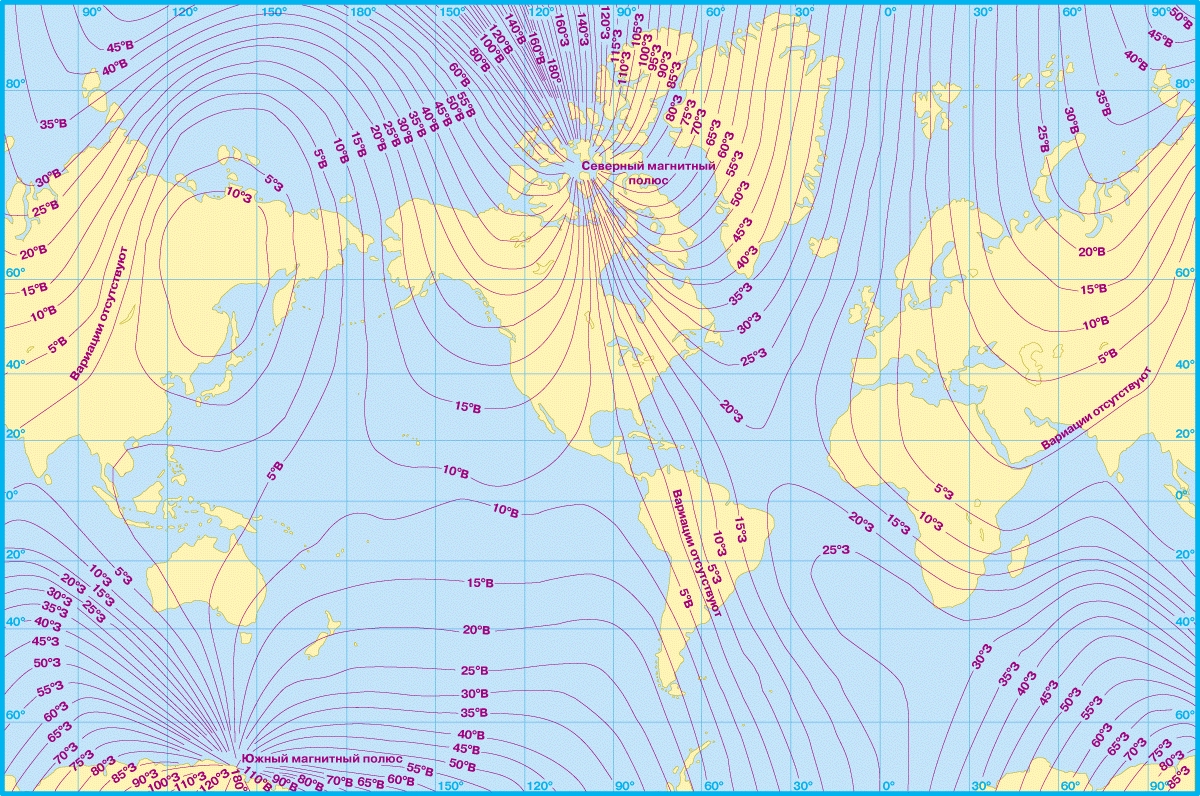
Рис. 1. МИРОВАЯ КАРТА ИЗОГОН
В дополнение к магнитным съемкам высокоточные наблюдения за магнитным полем Земли ведутся во всех частях мира в магнитных обсерваториях. Со спутников осуществляются магнитные съемки на больших высотах, где не существует влияния региональных магнитных аномалий, таких, как намагниченные тела в земной коре, например железные руды.
Магнитные измерения. В магнитных обсерваториях через регулярные интервалы времени определяют абсолютные значения магнитных элементов (а не их вариаций) с возможно большей точностью. Магнитное склонение D определяется путем измерения азимута (горизонтального направления) стрелочного магнита, свободно подвешенного на некрученой нити таким образом, что магнит располагается горизонтально. Азимут отсчитывается от направления на географический север, который устанавливается с помощью астрономических или геодезических наблюдений. Стандартными приборами магнитное склонение определяется с точностью 0,1'. Первоначально магнитное наклонение I определялось путем измерения наклона магнитной стрелки, центр которой закреплен на горизонтальной оси; эта ось ориентируется перпендикулярно магнитному меридиану таким образом, что стрелка может поворачиваться в плоскости меридиана. Однако точность этих измерений была невысокой, поэтому стали пользоваться индукционным наклономером, состоящим из круглой многовитковой катушки, которая вращается с большой скоростью вокруг оси, проходящей вдоль диаметра катушки. Ось прикрепляется к рамке таким образом, что ее ориентация может быть измерена. Этот метод основан на возникновении в катушке индуцированного электрического тока при изменении проходящего через нее магнитного потока. Если направление оси катушки не совпадает с направлением магнитного поля, то внутри катушки индуцируется переменный ток. Направление магнитного поля определяется в момент, когда гальванометр не показывает индуцированного тока во вращающейся катушке. С помощью индукционного наклонометра магнитное наклонение может быть установлено с точностью до 0,1'. Интенсивность горизонтальной составляющей измеряется методом, который разработал Гаусс. Измерения выполняются в два этапа. Вначале измеряется период крутильных колебаний свободно вращающегося в горизонтальной плоскости магнита; этот период зависит от напряженности геомагнитного поля H, а также от магнитного момента M и момента инерции магнита. Затем к магниту прикрепляют немагнитную полоску с известным моментом инерции, после чего эксперимент повторяют. Благодаря добавлению момента инерции период колебаний изменяется, что позволяет вычислить произведение MH. На втором этапе измеряют отклонение магнитной стрелки под влиянием земного магнитного поля и под действием поля магнита, использованного в первом эксперименте, получая отношения M/H. Комбинируя обе величины, MH и M/H, можно установить H. Сходным образом измеряют вертикальную компоненту Z. Если определено H и Z, магнитное наклонение может быть найдено из соотношения tg I = Z /H.
Протонный магнитометр. Его действие основано на ядерной прецессии (изменении ориентации оси вращения) вокруг направления магнитного поля. Ядра водорода (протоны), находящиеся в воде, под влиянием искусственного магнитного поля, ориентированного примерно под прямым углом к земному магнитному полю, поляризуются. Затем поляризующее магнитное поле внезапно выключается. Протоны начинают свободно прецессировать вокруг направления земного магнитного поля F до тех пор, пока ядерные спины не достигнут нового равновесного состояния. Прецессия протонов индуцирует небольшую электродвижущую силу в катушке. Частота f этого сигнала такая же, как частота прецессии протонов и связана с величиной магнитного поля F соотношением 2pf = gF, где g - гиромагнитное отношение протона, известное с высокой точностью. Измерение частоты сигнала в катушке позволяет определить общую магнитную интенсивность. Сконструированы также протонные магнитометры для измерения H и Z. При измерении каждого из этих компонентов используется пара колец Гельмгольца (катушки для создания чрезвычайно однородного магнитного поля) с тем, чтобы привести к нулевому значению компонент, который в данный момент не подлежит измерению.
Вековые магнитные вариации. Годовые средние значения магнитных элементов, измеренные в обсерваториях, и результаты магнитных съемок, выполненные с интервалом в несколько лет, показывают, что земное магнитное поле подвергается вековым (медленно меняющимся) вариациям. Эти вариации наносят на карты в виде линий равных значений годовых изменений (карты изовариаций, или изопор) определенных эпох. Изопоры образуют овалы вокруг регионов, где происходят быстрые годовые изменения. В течение одной или двух декад изопоры могут существенно изменяться. Их центры имеют тенденцию к дрейфу в западном направлении. Наблюдается также медленное вращение направления поля вокруг некоторого фиксированного направления. Например, наблюдения в Лондонской обсерватории показывают, что магнитное поле совершило почти три четверти оборота за последние 400 лет.
Палеомагнетизм. Изучение магнетизма, "сохраненного" в минералах и горных породах, обеспечивает информацию об истории земного магнитного поля в геологическом прошлом. Если горячее вещество охлаждается в магнитном поле от температуры выше точки Кюри (температура, выше которой намагниченное вещество теряет свою намагниченность) до более низких температур, его остаточная намагниченность будет сохранять направление внешнего магнитного поля, существовавшего при охлаждении. Поэтому сформировавшиеся из расплава минералы "запоминают" направление геомагнитного поля. Кроме того, при осадконакоплении намагниченные частицы в водных бассейнах ориентируются под воздействием земного магнитного поля. Эти феномены лежат в основе палеомагнетизма, но их интерпретация исключительно сложна, поскольку магнетизм пород не всегда стабилен. Палеомагнитные данные легли в основу теории дрейфа материков. В результате исследований разновозрастных горных пород было установлено, что их намагниченность отклоняется от направления современного магнитного поля. Таким образом, создается впечатление, что магнитные полюса в геологическом прошлом перемещались относительно поверхности Земли. Это интерпретируется как свидетельство того, что взаимное расположение материков в разные геологические эпохи менялось. Природа магнитного поля Земли и его вековых вариаций. Главное дипольное магнитное поле Земли можно было бы объяснить, если бы она была однородно намагничена. Однако намагниченность пород поверхностных слоев противоречит этому. Лабораторные эксперименты показывают, что точка Кюри понижается с увеличением давления. Поскольку давление и температура увеличиваются с глубиной, представляется весьма маловероятным, что ниже определенной глубины ферромагнитные вещества могут сохранять свою намагниченность. Хотя лабораторные эксперименты не полностью моделируют температуру и давление в глубоких слоях Земли, принято считать, что главное магнитное поле Земли не может быть обусловлено постоянной намагниченностью земного вещества. Сейсмические и другие геофизические данные показывают, что Земля обладает ядром (сходным по плотности с железом или железо-никелевым сплавом), которое находится на глубине ок. 2900 км и обнаруживает некоторые свойства жидкости. У.Эльзассер, Э.Буллард и другие ученые предположили, что в ядре происходят конвективные движения. Перемещение проводящего вещества в магнитном поле индуцирует электродвижущую силу, которая вызывает электрические токи, порождающие дополнительное магнитное поле подобно действию самовозбуждающейся динамо-машины. Магнитное поле вблизи центров векового хода может быть хорошо представлено изолированными диполями, расположенными вблизи поверхности "жидкого" ядра Земли. Относительно короткое время, за которое происходят вековые вариации, подтверждает, что их причина связана с движениями в ядре. Электрические токи, индуцируемые этими перемещениями вблизи поверхности ядра, вероятно, приводят к возникновению вековых вариаций.
Вариометры. В дополнение к абсолютным измерениям геомагнитного поля магнитные обсерватории ведут непрерывную запись компонентов H, D и Z, поскольку происходят регулярные и нерегулярные вариации магнитного поля. Амплитуда этих вариаций гораздо меньше, чем напряженность постоянного магнитного поля. Приборы для измерения вариаций называются вариометрами. Их действие основано на том, что изменения каждого магнитного элемента вызывают соответствующее отклонение магнитной стрелки, к которой прикрепляется зеркальце, а на него направляется свет от маленькой лампы. Отраженный луч падает на поверхность покрытого фотобумагой цилиндра, который вращается с постоянной скоростью вокруг своей оси. В вариометрах, одновременно измеряющих три компонента поля, фиксируются сразу три кривых на одной магнитограмме (рис. 2). Для регистрации вариаций различной амплитуды и частоты используют разные типы вариометров.
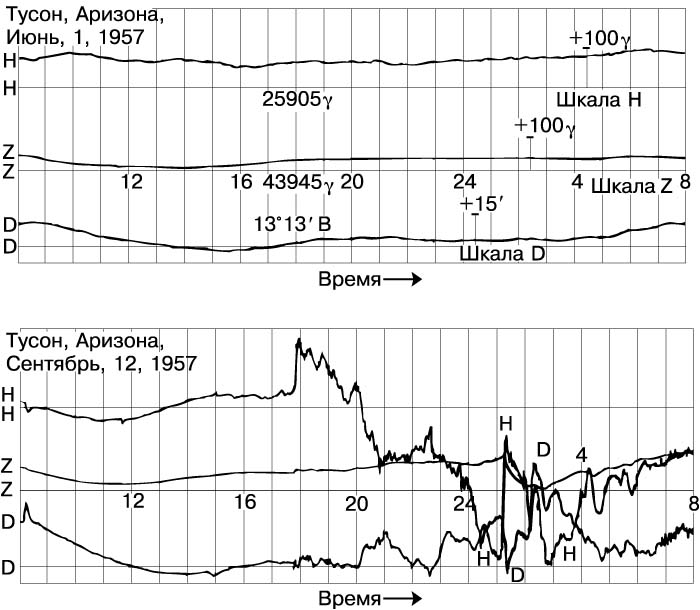
Рис. 2. МАГНИТОГРАММЫ ЯВЛЕНИЙ в земной атмосфере, полученные в Тусоне (Аризона, США). Верхняя магнитограмма показывает запись в магнитоспокойный день, нижняя - во время магнитной бури.
Квантовый магнитометр. Для наблюдений за быстропротекающими вариациями разработан магнитометр на парах рубидия. Этот прибор использует оптическую накачку (см. также ЗЕЕМАНА ЭФФЕКТ). Свет от рубидиевой лампы проходит через камеру, содержащую пары рубидия, и падает на фотоэлемент, регистрирующий интенсивность света. Магнитометр ориентируют так, чтобы луч света располагался почти параллельно магнитному полю. Если приложить переменное магнитное поле, создаваемое катушкой и имеющее частоту, соответствующую одному из зеемановских переходов в атомах рубидия, то увеличится поглощение за счет магнитного резонанса. Частота, соответствующая зеемановскому переходу, представляет собой известную функцию напряженности магнитного поля. Резонансная частота определяется частотой прилагаемого магнитного поля, что позволяет установить интенсивность магнитного поля. Магнитометр на парах рубидия приемлем для точных измерений быстро меняющихся вариаций магнитного поля, поскольку с его помощью может быть достигнута чувствительность порядка 0,02 гаммы (1 гамма = 10-5 гаусс = 10-9 тесла = 1 нТ). Для измерения абсолютных значений интенсивности используют протонный магнитометр.
Солнечные и лунные магнитные вариации. В соответствии с характером записи вариаций на магнитограмме выделяются "магнито-спокойные" и "магнито-возмущенные" дни. Эти магнитные возмущения гораздо более часты и интенсивны в полярных широтах.
Даже в идеально спокойных условиях записи на одной станции магнитные элементы H, D и Z систематически изменяются в зависимости от времени. Эти вариации носят название солнечно-суточной спокойной магнитной вариации и обозначаются Sq; здесь S показывает, что вариация зависит от местного времени обсерватории (т.е. от ее долготы относительно Солнца), а индекс q означает "спокойный". К северу и югу от экватора вплоть до 30° вариация Sq горизонтальной составляющей H соответственно увеличивается (в северном направлении) в течение дневного времени с максимумом вблизи полудня и уменьшается (в южном направлении) в ночное время; фаза вариации меняется на обратную к северу или югу от экваториального пояса. В северном полушарии Sq склонения D имеет направление на восток в утренние часы и на запад - в послеполуденное время; то же самое относится к вертикальной составляющей Z, которая уменьшается к ночи. Эти изменения D и Z меняют свой знак на обратный к югу от экватора. Если рассматривать все три элемента совместно, Sq имеет амплитуду, гораздо большую днем, чем ночью, что указывает на то, что Sq возникает в результате электрических токов, текущих в ионосфере. Электрические токи, ответственные за возникновение Sq, измеряются с помощью геофизических ракет, запускаемых вблизи экватора. Осредненные за месяц или год величины амплитуд Sq меняются в соответствии с изменением солнечной активности; они наибольшие, когда на Солнце наблюдается максимум пятен. Амплитуда Sq и, до некоторой степени, ее глобальное распределение ежедневно меняются; тем не менее в этих изменениях не наблюдается простого следования за солнечной активностью. Имеются и другие регулярные вариации, наложенные на Sq и меняющиеся в зависимости от лунного времени. Эти вариации, названные "лунно-суточными вариациями" (L), представлены главным образом регулярными полусуточными изменениями магнитного поля. Их амплитуда гораздо меньше, чем амплитуда Sq, например, вариация Sq горизонтальной составляющей H колеблется в пределах 30 гамм в низких широтах; колебания L - лишь ок. 3 гамм. Вариация L, в отличие от Sq, почти не выражена на магнитограммах (за исключением геомагнитного экватора, где ее величина необычно велика). Ее можно выделить лишь на основе тонкого математического анализа, в котором Sq и другие вариации подвергаются осреднению. Хотя L варьирует в зависимости от лунного времени, в основном она изменяется в дневные часы, когда электропроводность ионосферы максимальна. Следовательно, вариация L обязана электрическим токам, индуцируемым приливными движениями в нижних слоях ионосферы. В пределах узкого пояса над магнитным экватором Sq значительно возрастает в полуденные часы. Этот эффект обусловлен существованием "электроджета" - концентрированного электрического тока, текущего в пределах узкого пояса в ионосфере. Лунно-суточная вариация L возрастает с большей скоростью, чем Sq. Полагают, что экваториальный электроджет, текущий с запада на восток, возникает вследствие повышения электропроводности в направлении поперек магнитного поля (которое в этой области направлено горизонтально).
Магнитные бухты. Часто наблюдаются магнитные вариации, при которых линия записи H на магнитограмме своим очертанием напоминает бухту, образованную береговой линией. "Магнитные бухты" имеют максимальную амплитуду и наиболее часто наблюдаются в авроральных зонах (зонах полярных сияний) с ночной стороны Земли, по одной в каждом полушарии; их центры отстоят от геомагнитных полюсов на 23°. Типичная магнитная бухта указывает на интенсивный электроджет в ионосфере в западном направлении, протекающий через авроральную зону в ранние утренние часы (по местному времени), и более слабый электроджет, текущий в восточном направлении в поздние вечерние часы. Рассеянные токи от этих авроральных электроджетов распространяются над всей Землей и возбуждают магнитные бухты гораздо меньшей интенсивности в низких широтах. Мощные магнитные возмущения в авроральных зонах, называемые полярными штормами, тесно связаны с областью распространения полярных сияний и других полярных возмущений.
Влияние солнечных вспышек. В результате наблюдений за Солнцем были обнаружены неожиданные вспышки вблизи солнечных пятен. Одновременно с ними регистрируются возмущения на магнитограммах станций, расположенных на дневной стороне Земли. В земном магнитном поле солнечная вспышка вызывает неожиданное увеличение Sq длительностью 20-30 мин, поэтому эффект солнечной вспышки обозначают Sqa, где значок a указывает на увеличение интенсивности. В момент вспышки возрастает поток жесткого излучения от Солнца; это приводит к увеличению ионизации, росту электропроводности ионосферы и усилению электрического тока, вызывающего Sq. Резкое увеличение ионизации в более низких областях ионосферы вызывает заметное поглощение радиоволн и перерывы радиосвязи на большие расстояния.
Магнитная буря. Особенно интенсивные магнитные возмущения, распространяющиеся на весь земной шар, называют магнитными бурями. Некоторые магнитные бури начинаются неожиданно и почти одновременно по всей Земле, а другие развиваются постепенно. Признаком внезапно начинающейся магнитной бури служит резкое изменение всех трех магнитных элементов на магнитограмме. Горизонтальный компонент H внезапно увеличивает интенсивность, чему иногда предшествует небольшой отрицательный импульс. При внезапном начале бури амплитуда вариации максимальна в авроральных зонах и уменьшается по направлению к экватору; увеличение Sq и L наблюдается в пределах узкого пояса на магнитном экваторе в дневные часы. После внезапного начала бури линия записи горизонтального компонента H в течение нескольких часов обычно располагается выше уровня, предшествовавшего буре; этот этап (положительных значений) рассматривается как первая или начальная фаза. Значения H составляют от 10 до 20 гамм в средних широтах. За этой фазой следует существенное уменьшение до значений значительно ниже нормальных. Падение амплитуды на несколько десятков гамм во время бури средней интенсивности отвечает ее главной фазе. Максимальное отклонение достигается через 12 ч. Вслед за этим значительным уменьшением происходит медленное возвращение к нормальному уровню, которое обычно длится несколько дней. Эти особенности представляют собой осредненные характеристики магнитных бурь в средних и низких широтах; характеристики отдельных бурь могут существенно отличаться от средних. Крупные магнитные бури проходят эти фазы быстрее, чем слабые. По мере приближения к авроральной зоне на изменения магнитного поля, связанные с магнитной бурей, накладываются магнитные бухты. Изменения поля здесь гораздо более нерегулярные и интенсивные, чем в низких широтах; вариации во время бурь могут достигать нескольких тысяч гамм. В пределах полярных шапок (околополярные области внутри авроральной зоны) степень возмущения несколько меньше, чем в авроральной зоне, но гораздо более сильная, чем на низких широтах. Вариации в высоких широтах свидетельствуют о существовании интенсивных и концентрированных авроральных электроджетов, которые обычно направлены на восток перед "магнитной полночью" и на запад - после нее. Магнитная полночь определяется как время, когда Солнце располагается над магнитным меридианом, противоположным тому, на котором располагается станция; различие между локальной полночью и магнитной полночью зависит от положения станции (и в некоторой степени от времени года), это различие весьма незначительно в низких широтах, но в высоких широтах может достигать более одного часа. Электроджет, направленный к западу, гораздо сильнее ориентированного на восток; общая сила тока для бури средней интенсивности составляет 300 000 ампер и даже более во время максимума после магнитной полночи. Часто магнитные бури происходят через 1-2 дня после солнечной вспышки из-за прохождения Земли через поток частиц, выброшенных Солнцем. Исходя из времени запаздывания, скорость такого корпускулярного потока оценивают в несколько миллионов км/ч. Теория магнитных бурь была развита С. Чапменом, В. Ферраро, Х. Альфвеном, С. Зингером, А. Десслером, Е. Паркером и другими. Когда на некотором расстоянии от Земли поток солнечных частиц - протонов и электронов - сталкивается с земным магнитным полем, это вызывает "магнитный удар", который в виде сильной гидромагнитной ударной волны проходит через окружающий Землю электропроводящий газ. Внезапное начало магнитной бури означает приход гидромагнитной ударной волны. Солнечный газ, обволакивая Землю, сжимает ее магнитное поле и, следовательно, увеличивает его интенсивность. Рост магнитного поля в начальной фазе магнитной бури происходит как следствие этого эффекта. Некоторые из солнечных частиц захватываются земным магнитным полем на расстоянии более 40 000 км от Земли. Когда движение заряженной частицы в магнитном поле ориентировано косо по отношению к магнитной силовой линии, она перемещается по спирали вокруг этой линии. По мере того, как она вторгается в область с интенсивным магнитным полем, составляющая ее скорости, параллельная вектору напряженности поля, постепенно уменьшается, а скорость вращения возрастает, при этом общая скорость остается постоянной. Когда параллельная полю составляющая скорости становится нулевой, частица как бы отражается и начинает двигаться назад вдоль силовой линии, продолжая спиралевидное вращение вокруг нее (точка, где происходит отражение, называется "точкой магнитного зеркала", по аналогии с обычным оптическим зеркалом, отражающим свет). Таким образом, захваченные магнитным полем заряженные частицы, вращаясь по спирали вокруг силовых линий, колеблются между двумя зеркальными точками, одна из которых расположена в северном, а другая - в южном полушарии. Магнитное поле ослабевает с увеличением расстояния от Земли, из-за чего увеличивается радиус кривизны спирального движения частиц вокруг силовых линий на внешней части траектории. К тому же магнитные силовые линии выгнуты наружу, поэтому колеблющиеся вдоль них частицы испытывают центробежное ускорение, направленное от Земли, что способствует увеличению радиуса кривизны траектории частицы в ее части, более удаленной от Земли по сравнению с более близкой к Земле. А поскольку протоны и электроны вращаются вокруг магнитных силовых линий в противоположных направлениях, эти эффекты вызывают дрейф протонов в западном направлении, а электронов - в восточном. Суммарная скорость дрейфа зависит от энергии частицы и угла, образованного вектором ее скорости с силовой линией, когда частица пересекает экватор. Эти два фактора лежат в некотором диапазоне, поэтому частицы имеют различные скорости дрейфа и, захваченные земным магнитным полем, быстро распределяются, формируя оболочку вокруг Земли. Западный дрейф протонов и восточный дрейф электронов есть не что иное, как электрический ток, "размазанный" по оболочке. Этот ток, имеющий повсюду западное направление, генерирует магнитное поле, направленное так, что оно ослабляет магнитное поле Земли. Этим можно объяснить особенности главной фазы магнитной бури.
Микропульсации. Они представляют собой быстрые колебания небольшой амплитуды, которые наблюдаются как в спокойные, так и в возмущенные периоды. В средних и низких широтах часто наблюдаются два условных класса микропульсаций: Pc и Pt. Микропульсации Pc продолжаются более или менее непрерывно в течение многих часов с периодом от 10 до 60 сек; их амплитуда составляет порядка 0,1 гамма. Pt состоят из рядов пульсаций с небольшой амплитудой, каждый ряд продолжается от 10 до 20 мин, индивидуальные пульсации имеют период от 40 с до нескольких минут и амплитуду ок. 0,5 гаммы. Пульсация Pc происходит наиболее часто в утренние часы. Pt часто ассоциируется с магнитными бухтами и наблюдается чаще всего ночью. При использовании более чувствительных приборов, чем обычные вариометры, выявляются пульсации с более короткими периодами. С достаточной надежностью наблюдались колебания с частотой 2 Гц, но, возможно, существуют пульсации и с большей частотой. Амплитуда быстрых пульсаций очень мала - порядка 0,1 гаммы или меньше. Для их измерения используется катушка с большим числом витков проволоки (до 20 000) или огромная проволочная петля, охватывающая площадь 50-75 км2, а также квантовые магнитометры. В авроральных зонах и вблизи них выявлены гигантские микропульсации с амплитудой, значительно большей, чем у Pc, достигающей нескольких десятков гамм. Огибающая гигантской микропульсации постепенно возрастает и уменьшается с периодом от одной до нескольких минут. В авроральной зоне также выявлены пульсации с периодами в несколько минут, некоторые из них состоят из нескольких почти синусоидальных колебаний, продолжающихся в течение нескольких часов. Наиболее часто они возникают в годы высокой солнечной активности. В авроральной зоне наблюдаются и более быстрые микропульсации с периодом от нескольких секунд до 30 с, связанные, по-видимому, с авроральной активностью. Феномен гигантских микропульсаций не вполне исследован. Высказывается предположение, что некоторые их типы обусловлены колебаниями магнитных силовых линий во внешней области атмосферы Земли.
Геомагнитное поле в высоких слоях атмосферы. С началом запуска ракет и спутников в высокие слои атмосферы геомагнитное поле стало предметом пристального интереса. Раньше полагали, что земное магнитное поле простирается на большие расстояния. Л.Бирман предположил, что хвосты комет, состоящие из ионов, вытягиваются в сторону от Солнца под напором непрерывно испускаемого им потока заряженных частиц. По его расчетам, плотность ион-электронных пар вблизи Земли составляет ок. 100/см3. Идея была поддержана Е.Паркером, который назвал этот непрерывный корпускулярный поток "солнечным ветром". По его расчетам, если солнечный ветер действительно существует, земное магнитное поле должно быть сосредоточено в ограниченной области вокруг Земли, размер и форма которой зависят от силы солнечного ветра. Согласно данным магнитометра, установленного на космическом аппарате "Пионер-1" (1958), граница земного магнитного поля в направлении Солнца находится на расстоянии ок. 80 000 км от Земли (магнитосфера Земли). За пределами этой зоны зарегистрировано магнитное поле интенсивностью порядка 10 нТ. В межзвездном пространстве существует магнитное поле порядка 0,1 нТ. Важное открытие было сделано группой ученых под рук. Дж. Ван Аллена в 1958. С помощью приборов, установленных на первом в США спутнике "Эксплорер-1", они обнаружили, что во внешней атмосфере Земли существует радиация высокой интенсивности. Измерения, проделанные с советских спутников под руководством С.Н.Вернова и А.Е.Чудакова (1958), выявили вторую зону радиации. Эти зоны получили название радиационных поясов, или поясов Ван Аллена. Первый пояс простирается от 960 до 8000 км над земной поверхностью; второй - от 16 000 до 64 000 км. В пределах внутреннего пояса имеются протоны с высокой энергией. Протоны малой энергии и электроны заполняют более обширную область. Захват заряженных частиц земным магнитным полем впоследствии был проверен в экспериментах "Аргус" (1958), когда с помощью ядерного взрыва на больших высотах во внешние слои атмосферы были искусственно введены электроны. Оказалось, что захваченные электроны остаются в тонкой оболочке магнитосферы в течение нескольких дней.
Земные токи. Земные, или теллурические, токи текут в приповерхностном слое земной коры. Косвенно об их существовании можно заключить на основе измерений потенциометром разности потенциалов между двумя электродами, помещенными в грунт. Измеренная разность потенциалов представляет собой электродвижущую силу, возникающую в результате электрических токов, величина которых зависит от сопротивления коры. Величина сопротивления (от 100 до нескольких миллионов и более ОмЧсм) зависит от геологической структуры и заметно меняется с глубиной. Поскольку верхний слой коры земной обладает электропроводностью, меняющееся магнитное поле индуцирует в нем электрические токи. Например, магнитная вариация Sq индуцирует глобальные земные токи. Поскольку сопротивление Земли не изотропно, земные токи обладают преимущественным направлением. Исследование земных токов в авроральных зонах служит хорошим индикатором полярных возмущений, а также полезны для изучения микропульсаций.
ЛИТЕРАТУРА
Акасору С., Пелмен С. Солнечно-земная физика, ч. 1-2, М., 1974-1975 Вакье В. Геомагнетизм в морской геологии. Л., 1976 Яновский Б.М. Земной магнетизм. Л., 1978 Белов К.П., Бочкарев Н.Г. Магнетизм на Земле и в космосе. М., 1983
ге́омагнети́зм, ге́омагнети́змы, ге́омагнети́зма, ге́омагнети́змов, ге́омагнети́зму, ге́омагнети́змам, ге́омагнети́змом, ге́омагнети́змами, ге́омагнети́зме, ге́омагнети́змах
- Магнитное поле Земли.
- Раздел геофизики, в котором изучается распределение в пространстве и изменения во времени магнитного поля Земли, а также связанные с ним геофизические процессы в Земле и её магнитосфере.
ге́омагнети́ческий, ге́омагнети́ческая, ге́омагнети́ческое, ге́омагнети́ческие, ге́омагнети́ческого, ге́омагнети́ческой, ге́омагнети́ческих, ге́омагнети́ческому, ге́омагнети́ческим, ге́омагнети́ческую, ге́омагнети́ческою, ге́омагнети́ческими, ге́омагнети́ческом, ге́омагнети́ческ, ге́омагнети́ческа, ге́омагнети́ческо, ге́омагнети́чески
Геомагни́тные координа́ты - широта Ф и долгота λ, определяющие положение точки на земной поверхности при рассмотрении явлений земного магнетизма. Широта Ф - угловое расстояние от геомагнитного экватора (в плоскости геомагнитного меридиана) до рассматриваемой точки; долгота λ - двугранный угол между плоскостями геомагнитного меридиана, проходящего через данную точку на поверхности Земли, и геомагнитного меридиана, проходящего через географический полюс.
* * *
ГЕОМАГНИТНЫЕ КООРДИНАТЫ - ГЕОМАГНИ́ТНЫЕ КООРДИНА́ТЫ, широта Ф и долгота L, определяющие положение точки на земной поверхности при рассмотрении явлений земного магнетизма (см. МАГНЕТИЗМ). Широта Ф - угловое расстояние от геомагнитного экватора (см. ЭКВАТОР ГЕОМАГНИТНЫЙ) (в плоскости геомагнитного меридиана (см. МЕРИДИАН ГЕОМАГНИТНЫЙ) ) до рассматриваемой точки; долгота L- двугранный угол между плоскостями геомагнитного меридиана, проходящего через данную точку на поверхности Земли, и геомагнитного меридиана, проходящего через географический полюс (см. ПОЛЮСЫ ГЕОГРАФИЧЕСКИЕ) .
ГЕОМАГНИТНЫЕ КООРДИНАТЫ - Широта Ф и долгота ? , определяющие положение точки на земной поверхности при рассмотрении явлений земного магнетизма. Широта Ф - угловое расстояние от геомагнитного экватора (в плоскости геомагнитного меридиана) до рассматриваемой точки; долгота ? - двугранный угол между плоскостями геомагнитного меридиана, проходящего через данную точку на поверхности Земли, и геомагнитного меридиана, проходящего через географический полюс.
Геомагни́тные по́люсы - точки пересечения магнитной оси Земли с её поверхностью. В первом приближении можно считать, что Земля является однородно намагниченным шаром, магнитная ось которого составляет угол около 11,5º с осью вращения Земли.
* * *
ГЕОМАГНИТНЫЕ ПОЛЮСЫ - ГЕОМАГНИ́ТНЫЕ ПО́ЛЮСЫ, точки пересечения магнитной оси Земли с ее поверхностью. В первом приближении можно считать, что Земля является однородно намагниченным шаром, магнитная ось которого составляет угол ок. 11,5° с осью вращения Земли (см. ЗЕМНАЯ ОСЬ) .
ГЕОМАГНИТНЫЕ ПОЛЮСЫ - точки пересечения магнитной оси Земли с ее поверхностью. В первом приближении можно считать, что Земля является однородно намагниченным шаром, магнитная ось которого составляет угол ок. 11,5. с осью вращения Земли.
прил.
1. соотн. с сущ. геомагнетизм, связанный с ним
2. Свойственный геомагнетизму, характерный для него.
3. Связанный с изучением геомагнетизма.
ге́омагни́тный, ге́омагни́тная, ге́омагни́тное, ге́омагни́тные, ге́омагни́тного, ге́омагни́тной, ге́омагни́тных, ге́омагни́тному, ге́омагни́тным, ге́омагни́тную, ге́омагни́тною, ге́омагни́тными, ге́омагни́тном, ге́омагни́тен, ге́омагни́тна, ге́омагни́тно, ге́омагни́тны, ге́омагни́тнее, поге́омагни́тнее, ге́омагни́тней, поге́омагни́тней
геомагнитофо́н
(см. гео... + магнитофон) геофон, усиливающий и регистрирующий трудноуловимые звуковые волны в горных породах; примен. при горноспасательных работах в шахтах.
- Приёмник звуковых волн, снабжённый специальной приставкой для регистрации трудноуловимых звуков в подземных горных выработках.
геомант - землегадатель по сделанным наудачу точкам
Ср. Монастырки знали, что сама их патронесса (Ментенон), труся смерти, запиралась с бродячими гадальщицами на картах и с астрологами... и прибегала к открытиям геомантов, к заклинателям беса и толкователям снов.
Данилевский. На Индию. 1, 2.
Ср. Geomancie (γη, земля - μαντεύειν, гадать) - гаданье, геомантия.
См. патрон.
ГЕОМАНТИЯ - ГЕОМА́НТИЯ (от гео- и греч. manteia, гадание), способ гадания, широко распространившийся в Европе с конца 13 в., основанный на интерпретации различных знаков на земной поверхности. Эта эзотерическая традиция возникла на Ближнем Востоке, потом распространилась в Африке и Европе. Европейцы позаимствовали этот способ гадания у арабов, которые узнавали будущее, интерпретируя фигуры или точки, случайным образом вычерченные острой палочкой на земле или песке. Геомантия являлась единственным гаданием, разрешенным законами шариата (см. ШАРИАТ). Постепенно в Западной Европе сложилась отдельная магическая система предсказаний, основанных на прочтении шестнадцати символов-элементов, различаемых на земной поверхности, а для определения результата главное значение имеет четность или нечетность количества нанесенных точек или линий. Форма рисунка часто фиксировалась при помощи камешков, количество и расположение которых определяло четыре линии, формирующие символ.
Геомантия является западным аналогом восточной бинарной системы гадания, известной как Ицзин (см. ИЦЗИН). В геомантии используются 16 основных символов, каждый из которых состоит из четырех линий, сформированных точками, число линий может быть четным или нечетным (Народ - Путь - Союз - Тюрьма - Удачная судьба - Неудачная судьба - Прибыль - Убыток - Печаль - Радость - Красный - Белый - Девочка - Мальчик - Голова - Хвост). Как и в гадании Ицзин, в геомантии 16 символов интерпретируются при помощи особой системы соответствий, в частности 16 символов изначально классифицировались при помощи планет и знаков Зодиака. Каждый из 16-ти символов состоит из двух верхних и двух нижних линий, образуя четыре биграммы. Верхняя биграмма является отправной точкой в гадании, поскольку в геомантии верхняя линия олицетворяет начало, в нижняя - конец. В этом состоит отличие геомантии от системы Ицзин, в которой гексаграммы начинаются с нижней линии и заканчиваются верхней.
ГЕОМАНТИЯ (греч. geomanteia, от ge - земля, и manteia - гадание). Гадание по проведенным на песке линиям и точкам.
Á сущ см. Приложение II
Сведения о старой норме ударения:
Неудивительно, если вы произносите данное слово по-иному. Ударение на третьем слоге, соответствующее греческому языку-источнику, ср. γεωμέτρης, долгое время приводилось словарями как вариант нормы. Вы также можете попадать под влияние аналогии: геоме́трия - геоме́тр. Отличное от современной нормы ударение встречается у поэтов:
Скажи мне, чертежник пустыни,
Арабских песков геоме́тр,
Ужели безудержность линий
Сильнее, чем дующий ветр?
О. Э. Мандельштам, «Скажи мне, чертежник пустыни...»
геоме́тр, геоме́тры, геоме́тра, геоме́тров, геоме́тру, геоме́трам, геоме́тром, геоме́трами, геоме́тре, геоме́трах
- Математик с циркулем.
- И Евклид, и Лобачевский.
- Именно так древние греки называли просто землемера.
ГЕОМЕТРАЛЬНЫЙ ая, ое. géométral adj. <, лат. geometralis. Изображенный со всеми измерениями, но без перспективы. Михельсон 1877. Всякой архитектор делает планы и геометральные фасады. Баженов 119. План Геометральной, или по Руски плоскость земле мерная. Витр. (к). 14. - Лекс. Сл. 18: геометральный 1768.
Геометриза́ция месторожде́ния - комплекс работ по сбору, систематизации, математической обработке и графическому изображению данных о структурных и качественных особенностях месторождения полезного ископаемого.
* * *
ГЕОМЕТРИЗАЦИЯ МЕСТОРОЖДЕНИЯ - ГЕОМЕТРИЗА́ЦИЯ МЕСТОРОЖДЕ́НИЯ, комплекс работ по сбору, систематизации, математической обработке и графическому изображению данных о структурных и качественных особенностях месторождения полезного ископаемого (см. МЕСТОРОЖДЕНИЕ ПОЛЕЗНОГО ИСКОПАЕМОГО) .
ГЕОМЕТРИЗАЦИЯ МЕСТОРОЖДЕНИЯ - комплекс работ по сбору, систематизации, математической обработке и графическому изображению данных о структурных и качественных особенностях месторождения полезного ископаемого.
геометриза́ция недр
(см. геометрия) горн, составление маркшейдерских планов (см. маркшейдерия), характеризующих условия залегания, качество и структуру месторождения полезного ископаемого.
Геометрия - раздел математики, тесно связанный с понятием пространства; в зависимости от форм описания этого понятия возникают различные виды геометрии. Предполагается, что читатель, приступая к чтению этой статьи, обладает некоторыми представлениями об элементарной геометрии, а также о законах арифметики и алгебры.
См. также
Первый важный вопрос: как описать наше понятие пространства? В поисках ответа перед нами открывается несколько возможностей, но проще, а возможно, естественнее и полезнее воспользоваться для этого понятиями "точка" и "прямая". Оба они коренятся в процессе визуального восприятия. Точку можно мысленно представлять как "точку зрения", из которой ведется наблюдение, а прямую, определяемую двумя объектами, считать состоящей из множества точек зрения, при наблюдении из которых один объект заслоняет другой. При таком подходе вводится понятие "прямизны", которое воплощается в термине "прямая линия" (или просто "прямая"). Можно считать, что мы абстрагировали понятия "точка" и "прямая" из окружающего мира. В нашем повседневном опыте коренится еще одно представление - о расстоянии АВ между точками А и В. (Мы говорим также о "длине" отрезка АВ.) О расстоянии мы судим, сравнивая его с некоторым эталоном. Одна из возможных единиц длины - метр; изготовив копии с эталона метра, мы сравниваем расстояния и говорим, что расстояние АВ больше (>), равно (=) или меньше (
(эллиптический параболоид)
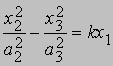
(гиперболический параболоид). Некоторые из этих поверхностей являются "линейчатыми". Это означает, что через каждую точку такой поверхности можно провести по крайней мере две прямые, целиком лежащие на этой поверхности; в результате получим два семейства прямых, любое из которых образует всю поверхность. Эти прямые называют образующими. Если мы ограничимся рассмотрением какой-нибудь одной плоскости, например, положив для этого в уравнении квадратичной поверхности x3 = 0, то получим уравнения конических сечений - кривых, по которым эти поверхности пересекают плоскость x3 = 0. Это - эллипс (частным случаем которого является окружность), гипербола и парабола
(см. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ; КОНИЧЕСКИЕ СЕЧЕНИЯ). Исследование геометрических мест точек, заданных уравнениями, порядок которых больше двух, значительно сложнее. В 1704 И.Ньютон (1643-1727) классифицировал кубические кривые, и с тех пор кривые и поверхности третьего и четвертого порядков стали предметом интенсивного изучения. Хотя методы Декарта существенно упростили идеи греческой геометрии, они же породили много новых трудностей. Некоторые из этих трудностей были преодолены с помощью средств, которыми располагал математический анализ 19 в. Справиться с другими удалось лишь позднее, когда была создана т. н. алгебраическая геометрия (см. АЛГЕБРАИЧЕСКАЯ ГЕОМЕТРИЯ). Интересно отметить, что аналитическая геометрия Ферма и Декарта появилась как раз в то время, когда И. Кеплер (1571-1630), исходя из многочисленных астрономических наблюдений, сделал вывод о том, что планеты движутся по эллипсам, в одном из фокусов которых расположено Солнце. Это подготовило почву для открытия Ньютоном закона всемирного тяготения. Природа даже тогда, когда речь шла о местоположениях далеких планет, соответствовала описанию человеком его представлений о пространстве! Нужно ли удивляться, что для Ньютона "абсолютное пространство по самой своей сущности, безотносительно к чему бы то ни было внешнему, остается всегда одинаковым и неподвижным". Для великого современника Ньютона Г. фон Лейбница (1646-1716) пространство было совокупностью всех возможных отношений расстояния. В следующем разделе мы будем понимать слово "пространство" в более ограниченном смысле.
Проективная геометрия. Наступление 17 в. ознаменовалось настоящим взрывом научной активности. В развитии математики началась новая эра; наряду с Декартом Ж. Дезарг (1593-1662) и Б. Паскаль (1623-1662) попытались по-новому и критически взглянуть на старую евклидову геометрию, чтобы понять, все ли ее результаты представимы в терминах одних лишь точек и прямых. К возникшей в результате такого критического пересмотра проективной геометрии можно подойти, вводя новую систему аксиом, но гораздо поучительнее рассмотреть наши предыдущие исходные допущения и попытаться понять, как их надлежит изменить. Если следовать зрительным восприятиям, то первое, что сразу подпадает под подозрение, - это постулат о параллельных прямых. Нам кажется, что такие прямые все-таки пересекаются в бесконечности. Предположим, что это действительно так, и дополним евклидову плоскость одной "идеальной точкой" или "бесконечно удаленной точкой", общей для любого множества параллельных прямых. Тогда утверждение о том, что прямые l и m параллельны, перейдет в утверждение о том, что прямые l и m пересекаются в бесконечности. Необходимо доказать, что все такие идеальные точки ведут себя так, как если бы они принадлежали "идеальной прямой", которая обладает всеми свойствами, которыми по предположению обладают обычные прямые. Доказательство этого утверждения основывается на знаменитой теореме Дезарга: если соответствующие вершины двух треугольников можно соединить тремя прямыми, пересекающимися в одной точке, то соответствующие стороны пересекаются в точках, лежащих на одной прямой, и обратно. Обосновав присоединение идеальных элементов к евклидовой плоскости, мы можем теперь сказать, что любые две прямые имеют точку пересечения, и в этом заключается основное отличие проективной геометрии. Аналогичным образом мы можем присоединить к трехмерному евклидову пространству "бесконечно удаленную плоскость" и построить проективное пространство любой размерности. Заметим, что теперь мы можем полностью отказаться от понятия "расстояние". Нужно подчеркнуть, что проективная геометрия не есть что-то абстрактное, практически не связанное с внешним миром. Рассмотрим произвольную точку Р и любую плоскость p, не проходящую через точку Р, в обычной евклидовой геометрии. Любая плоскость p1, проходящая через Р, пересекается с плоскостью p по некоторой прямой l1; в частности, плоскость pҐ , проходящая через точку Р и параллельная плоскости p, пересекается с p по прямой lҐ , бесконечно удаленной прямой, лежащей в плоскости p. Таким образом, существует взаимно однозначное соответствие между плоскостями, проходящими через точку Р, и прямыми, лежащими в плоскости p. Если воспользоваться интерпретацией точка = прямая, проходящая через Р, прямая = плоскость, проходящая через Р, то можно проверить, что все аксиомы проективной геометрии выполняются, а потому "пучок" прямых и плоскостей, проходящих через точку Р, образует проективную геометрию плоскости. Вклад Паскаля в геометрию заключается в том, что он показал проективную природу известных со времен Аполлония свойств конических сечений, которые позднее были переведены Декартом на алгебраический язык. Эта работа была завершена Ф. де Лаиром (1640-1718), и, хотя дальнейшее развитие проективной геометрии прервалось и затем продолжилось лишь в 19 в., начало критическому анализу понятия длины было положено.
Непрерывность. Понятие касательной к кривой восходит по крайней мере к Архимеду, но только после того, как Ферма и Ньютон осознали его значение для дифференциального исчисления, это понятие обрело удобную для приложений явную форму. Однако прошло немало лет, прежде чем О.Коши (1789-1857) придал строгость огромному числу теорем, разложениям в степенные ряды, решениям дифференциальных уравнений и т.п., что позволило математическому анализу занять в математике место, сравнимое с геометрией. Понятие числа точек на прямой ничему не соответствует в нашем опыте визуального восприятия пространства, и именно это привело Зенона Элейского к упомянутым выше комментариям. Есть два способа интерпретации понятия непрерывности в терминах интуитивных представлений об окружающем нас мире: 1) через скрупулезный анализ отношений между точками и прямыми и 2) в терминах движения, т.е. средствами математического анализа (см. МАТЕМАТИЧЕСКИЙ АНАЛИЗ).
Конечная геометрия. Хотя целые числа возникают не обязательно в связи с точками прямой, тем не менее естественно рассматривать их как числа, представляющие кратные некоторого единичного отрезка. Это позволяет придать рациональным числам геометрическую интерпретацию, известную еще древним грекам. Однако такой подход к числу недостаточно тонок и сталкивается с трудностями, на которые и указал Зенон; наша концепция пространства включает в себя понятие числа, но для определения чисел понятие пространства не подходит. Возвращаясь к аксиомам проективной геометрии
(см. ПРОЕКТИВНАЯ ГЕОМЕТРИЯ),
заметим, что они не содержат понятия длины и не имеют следствием бесконечность числа точек на прямой. То, что число точек на прямой может быть конечным, подтверждается следующим примером. Предположим, что под точками мы понимаем 15 символов (ab), (ac), (ad), (ae), (af), (bc), (bd), (be), (bf), (cd), (ce), (cf), (de), (df), (ef), где (ij) = (ji). Существуют 35 прямых, каждая из которых содержит три и только три из этих точек. Такие прямые можно разбить на два типа: 1) прямая типа I содержит три точки вида (аb), (bc), (ca); таких прямых 20; 2) прямая типа II содержит три точки вида (ab), (cd), (ef); таких прямых 15. Любая тройка точек, не принадлежащих ни к одному из этих двух типов, определяет некоторую плоскость; существуют 15 плоскостей, каждая из которых содержит семь точек и семь прямых. На прилагаемом рис. 5 показаны расположения точек и прямых на одной из этих плоскостей. (Заметим, что окружность представляет в конечной геометрии прямую.) Нетрудно проверить, что все аксиомы проективной геометрии выполняются, из чего мы заключаем, что они непротиворечивы, но такая геометрия не очень соответствует нашему представлению о пространстве. Чтобы перебросить мост между привычным понятием пространства и построенной нами геометрией, необходимо исследовать возможную связь между точками на прямой и числами арифметики.
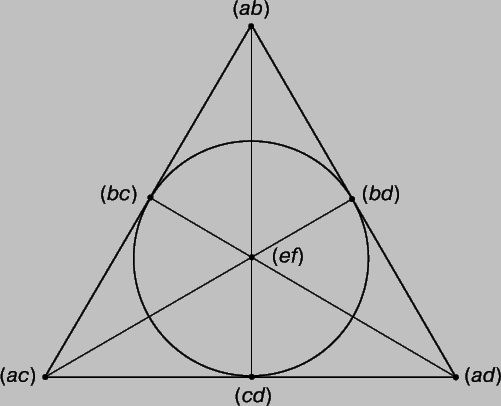
Рис. 5. ПЛОСКОСТЬ ОПРЕДЕЛЯЕТСЯ любыми тремя точками, не лежащими на одной прямой. Например, (ab), (ef), (bc) определяют одну плоскость.
Первым, кто предложил средства, позволяющие геометрически определять операции сложения и умножения, был немецкий математик К.Штаудт (1798-1867), но именно Д. Гильберт (1862-1943) продемонстрировал, что законы арифметики в их геометрической интерпретации зависят от двух теорем - Дезарга и Паппа. В случае конечной геометрии из теоремы Дезарга следует теорема Паппа, а потому если она верна, то верна и теорема Паппа. В этом случае и сложение, и умножение ассоциативны, коммутативны и дистрибутивны, и координаты, которые можно поставить в соответствие точкам на прямой, могут образовать конечное "поле". Если число точек на прямой бесконечно (например, если точки на прямой, за исключением бесконечно удаленной точки, могут быть поставлены во взаимно однозначное соответствие с рациональными числами), то "сложение" точек на прямой ассоциативно и коммутативно при условии, что выполняется теорема Дезарга. Если размерность n > 2, то это заведомо так. Однако из семи аксиом проективной геометрии теорема Паппа не следует; это означает, что умножение, будучи ассоциативным, необязательно коммутативно. При n = 2 теорема Дезарга может не выполняться, и "алгебра" точек на прямой еще более усложняется. Возможные недезарговы плоскости исследуются с 1902, но многое еще остается неизвестным. Если потребовать, чтобы для каждого действительного числа нашлась соответствующая ему точка на прямой, то мы получим т.н. "непрерывную" геометрию. Это требование выполняется введением дополнительного предположения, которое в свою очередь можно использовать для доказательства теоремы Паппа. Такая аксиома непрерывности описывает тот аспект нашего понятия пространства, который был Лейбницем охарактеризован как "лабиринт континуума". Тем не менее роль алгебры в геометрии стала очевидна, и в дальнейшем обе эти ветви математики стали нерасторжимы.
Дифференциальная геометрия. Определив касательную к плоской кривой в точке (y1, y2) с помощью "углового коэффициента" m = dy2/dy1, мы можем записать ее уравнение в виде
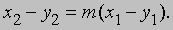
Записанное с помощью дифференциалов, это уравнение принимает вид
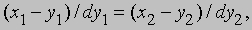
и его непосредственное обобщение приводит к уравнениям касательной к неплоской кривой в точке (y1, y2, y3):
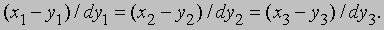
В то время как понятие углового коэффициента не допускает обобщения, понятие направляющего числа легко обобщается, и в качестве направляющих чисел рассматриваемой прямой можно принять дифференциалы. Уравнение соприкасающейся плоскости (плоскости касательных) к неплоской кривой задается определителем
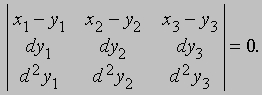
Все эти уравнения имеют явный вид, если рассматриваемое геометрическое место точек задано аналитически, например, параметрически формулами y1 = y1 (t), y2 = y2 (t), y3 = y3 (t). Дифференциальная геометрия стала самостоятельным разделом математики после того, как Б.Риман (1826-1866) заметил, что теорема Пифагора допускает дальнейшее обобщение, и предложил определять меру длины как
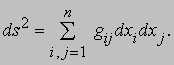
При n = 3 и gij = 1 (если i = j) и gij = 0 (если i № j) мы получаем евклидову геометрию в декартовых (прямоугольных) координатах; другие возможные выборы величин gij приводят к множеству новых геометрических систем, в частности, к геометрии специальной и общей теорий относительности. В конце 19 в. для разработки этих идей был изобретен тензорный анализ, который оказался одним из наиболее подходящих языков для современной физики. Таким образом, методы математического анализа привели нас к идеям, весьма отличным от тех, которые были известны древним грекам. В частности, огромное значение получило понятие "геодезической" - линии, целиком лежащей на поверхности и являющейся кратчайшим путем между двумя точками. Если уравнение некоторой поверхности записать в параметрическом виде: x1 = x1 (u,v), x2 = x2 (u,v), x3 = x3 (u,v), то геометрические места точек u = const, v = const называются "параметрическими кривыми" этой поверхности, а параметры (u,v) задают на этой поверхности "криволинейные координаты". На поверхности Земли мы определяем свое местонахождение, указывая "широту" и "долготу"; из этих двух систем параметрических кривых линии долготы являются большими кругами и, следовательно, геодезическими. В случае декартовой геометрии параметрическими кривыми служат прямые, параллельные осям координат, и все такие прямые - геодезические.
См. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ. Неевклидова геометрия. Смелое допущение Евклида о параллельных прямых, содержавшееся в его знаменитом пятом постулате, почти две тысячи лет было для математиков источником смутного беспокойства, но серьезные попытки доказать его на основе иных допущений были предприняты только в 18 в. И хотя они оказались безуспешными, математикам все же удалось показать, что постулат о параллельных Евклида эквивалентен требованию равенства суммы углов треугольника двум прямым углам, или, что то же, p радианам. Поэтому скорее психологическим, чем математическим прорывом стало осознание существования двух других возможных вариантов: 1) сумма углов треугольника всегда больше p; в этом случае параллельных прямых не существует, и любые две прямые пересекаются; 2) сумма углов треугольника всегда меньше p; в этом случае для любой точки Р, не лежащей на данной прямой l, существуют две прямые l' и l ", проходящие через Р и параллельные данной прямой l, и любая прямая, лежащая внутри угла, заключенного между l' и l ", не пересекается с l. Непротиворечивость второго варианта была осознана К. Гауссом (1777-1855), но впервые опубликована независимо друг от друга Я. Бойяи (1802-1860) и Н.И.Лобачевским (1792-1856) в 30-х годах 19 в. Риман был первым, кто понял, что первый вариант реализуется в сферической геометрии, развитой для нужд астрономии и мореплавания. Было бы ошибкой думать, будто математика на протяжении столетий не претерпела никаких изменений. Постижение тонких идей происходит медленно, и когда мы оглядываемся назад, в прошлое, наши величайшие достижения нередко представляются очень простыми. А. Кэли (1821-1895) и Ф. Клейн (1849-1925) прояснили связь между двумя упомянутыми вариантами, разработав в аналитической форме то, что ими было названо "эллиптической" и "гиперболической" геометриями. Евклидова геометрия является предельным случаем каждой из них, и это верно в отношении любой из аналитических формул таких геометрий. Большие круги (геодезические) на сфере, являющейся поверхностью постоянной положительной кривизны, играют роль прямых и порождают эллиптическую геометрию; аналогичным образом, на поверхности постоянной отрицательной кривизны геодезические порождают гиперболическую геометрию. Можно построить и другие наглядные и поучительные модели эллиптической и гиперболической геометрий, но важно сознавать, что все эти модели содержатся в более общем подходе Римана. Трудно переоценить философское значение этих идей. Человек словно снял темные очки и увидел свое представление о пространстве "при дневном свете", что открыло новые, более интересные и захватывающие возможности, чем он мог себе вообразить. То, что Гаусс предпринял попытку измерить сумму углов треугольника, образованного тремя горными вершинами в Германии, было естественным следствием его понимания того, что постулат Евклида о параллельных явился результатом выбора из ряда возможностей, хотя выбора, несомненно, наилучшего для наших повседневных нужд. И хотя Гауссу не удалось обнаружить никаких отклонений от p, выходящих за пределы допустимой экспериментальной ошибки, это отнюдь не положило конец попыткам предпринять аналогичные крупномасштабные измерения с помощью гигантских телескопов и электронных устройств (см. НЕЕВКЛИДОВА ГЕОМЕТРИЯ). В последние десятилетия наши представления о пространстве сильно изменились под воздействием повсеместного принятия в физике концепции "пространства-времени". Связывание воедино двух фундаментальных понятий вынуждает нас перенести все внимание с "положения" на "событие". Выбирая из многообразия римановых метрик некоторую, в чем-то более предпочтительную, мы может более удовлетворительным образом скоординировать результаты современной физики. См. ОТНОСИТЕЛЬНОСТЬ.
Понятие группы. Расцвет геометрических идей в 19 в. убедительно свидетельствовал о необычайной жизненности математических исследований в целом. Но, возможно, самым важным событием в развитии математического мышления в 19 в. стала постепенная кристаллизация понятия "группы" в алгебре и осознание его значения для геометрии. Древние греки вполне могли бы натолкнуться на эту идею, будь они более настойчивы в поиске внутреннего смысла симметрии. К проблеме симметрии можно подходить двояко. Если геометрическая фигура остается инвариантной относительно вращения или, более общо, относительно какого-нибудь "преобразования", то можно выписать некоторую систему уравнений, выражающих эти преобразования аналитически. Но возможен и другой подход: мы можем представить себе, что геометрическая фигура остается неизменной, а меняется избранный нами способ ее описания относительно системы координат. По существу речь идет о двух возможных способах интерпретации одного и того же преобразования, но иногда одна интерпретация бывает предпочтительнее другой. Если мы имеем в виду все возможные линейные преобразования, которые оставляют фигуру инвариантной, то говорим, что эти преобразования образуют "группу", которую абстрактно можно определить следующим образом. Если обозначить эти преобразования Т1, Т2 и т.д., а совокупность всех таких преобразований - G, то для любых двух преобразований Ti и Tj из G должны выполняться следующие условия: I. TiTj = Tk также принадлежит G; II. Ti (TjTk) = (TiTj)Tk (свойство ассоциативности); III. В G существует некоторое преобразование Т0, называемое тождественным преобразованием или единицей, такое, что TiT0 = T0Ti = Ti; IV. Для каждого Ti из G существует "обратное преобразование" Ti-1, такое, что TiTi-1 = Ti-1Ti = T0. Число g преобразований Т, содержащихся в G, называется "порядком" группы G. Существует 6 симметрий треугольника, они представлены на рис. 6. Нетрудно проверить, что если ограничиться только вращениями, то для тетраэдра g = 12, для куба и октаэдра g = 24, а для икосаэдра и додекаэдра g = 60. Если же кроме вращений допустить отражения и отражения с вращениями, то число g возрастет вдвое. То, что у куба и октаэдра должна быть одна и та же группа вращений, неудивительно, т.к. вершины одного многогранника служат центрами граней другого. Аналогичное утверждение справедливо относительно икосаэдра и додекаэдра. Эти фигура "двойственны" друг другу, тогда как тетраэдр "самодвойствен".
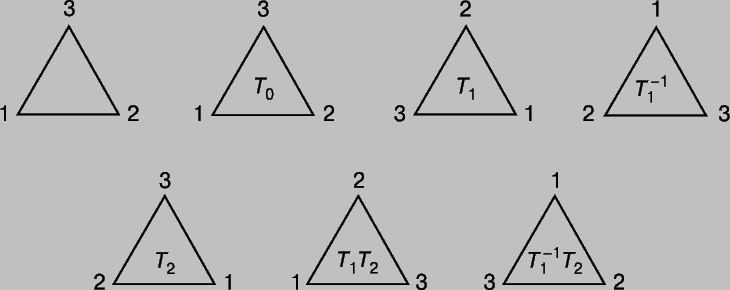
Рис. 6. ШЕСТЬ СИММЕТРИЙ ТРЕУГОЛЬНИКА. Любой из изображенных здесь треугольников может быть получен из первого соответствующим поворотом.
Все преобразования, о которых шла речь, линейны; они переводят точку в точку, прямую - в прямую и плоскость - в плоскость. Такие "коллинеации" имеют особое значение для описания нашего представления о пространстве, основанного на точках и прямых. Клейн первым понял, что множество всех линейных преобразований, оставляющих метрику инвариантной, позволяет адекватно описывать рассматриваемую геометрию, и это привело Клейна к классификации геометрий по их группам коллинеаций. В проективной геометрии метрика отсутствует, поэтому соответствующая ей группа называется "полной линейной группой". В евклидовой геометрии любое вращение оставляет инвариантной сумму квадратов координат, и соответствующая коллинеация называется "ортогональной"; т.к. комбинация двух ортогональных преобразований есть снова ортогональное преобразование, все ортогональные преобразования образуют "ортогональную группу". Параллельные переносы также оставляют метрику инвариантной, поэтому группа "перемещений фигуры как твердого тела" содержит ортогональную группу в качестве своей нормальной подгруппы. Такой подход к изучению геометрии был предложен Клейном в его Эрлангенской программе (1872), которая явилась большим шагом вперед, поскольку предлагала единую точку зрения на ранее существовавшие различные геометрии. Понятие группы получило дальнейшее развитие. До сих пор мы предполагали, что каждое преобразование линейно, но это ограничение несущественно, коль скоро каждое преобразование имеет обратное, которое однозначно определено. Исследование таких "бирациональных" преобразований в общем виде началось с работ Л. Кремоны (1830-1903). В 1870 было доказано, что любое бирациональное преобразование может быть порождено составными квадратичными преобразованиями. Важно подчеркнуть существование некоторых особых точек или геометрических мест, для которых взаимно однозначное соответствие нарушается; именно это обстоятельство порождает специфические проблемы алгебраической геометрии, над решением которых билось немало математиков.
См. также АЛГЕБРА АБСТРАКТНАЯ.
Топология. Общая теория групп преобразований была построена С. Ли (1842-1899), который почти в одиночку возделал огромную территорию математики, оказавшую впоследствии воздействие почти на все ее разделы. Что же касается влияния Ли на геометрию, то оно сказалось прежде всего на расширении самого смысла термина "геометрия", в результате чего граница между геометрией и анализом оказалась размытой. Та часть "ничейной земли", в которой алгебраический характер преобразования предается забвению, получила название "топологии". Топология имеет дело с взаимно однозначными и непрерывными преобразованиями, называемыми "гомеоморфизмами". Изучение топологических пространств позволило открыть множество красивейших теорем. С 1895, когда А.Пуанкаре впервые в явном виде рассмотрел гомеоморфные преобразования топологических пространств, и по сей день топология находится в состоянии интенсивного беспрецедентного развития. Поясним суть ее проблем на одном примере. Возьмем некоторую поверхность и будем ее рассматривать как резиновую пленку, которую можно сжимать и растягивать, но не рвать. Тогда никакие из разрешенных операций не могут преобразовать сферу в тор (бублик); число дыр в поверхности называется ее "родом" и является "топологическим инвариантом". Аналогичный инвариант существует и для односторонних поверхностей, таких как лист Мебиуса (см. также ТОПОЛОГИЯ). Существует масса примеров, когда к топологии обращаются в поисках новых, стимулирующих идей и подходов, чувствуя, что иначе "не пробиться", как, например, в теории контурного интегрирования Коши. Наше представление о пространстве - это наиболее изученная модель, позволяющая лучше всего понять те абстракции, которые и составляют суть математики в целом. Именно такая интерпретация слова "геометрия" позволила уяснить истинное значение этой науки и причину, по которой люди занимаются ее изучением на протяжении вот уже 2500 лет.
ГЕОМЕТРИЧЕСКАЯ АБСТРАКЦИЯ - ГЕОМЕТРИ́ЧЕСКАЯ АБСТРА́КЦИЯ, один из видов абстрактного искусства (см. АБСТРАКТНОЕ ИСКУССТВО), предпочитающий композиции, в основе которых - строгая ритмика геометрических или (в скульптуре) стереометрических фигур. Ее ранние варианты (отчасти орфизм (см. ОРФИЗМ) Р. Делоне (см. ДЕЛОНЕ Робер) и Ф. Купки (см. КУПКА Франтишек), а также супрематизм (см. СУПРЕМАТИЗМ) К. С. Малевича (см. МАЛЕВИЧ Казимир Северинович) и неопластицизм (см. НЕОПЛАСТИЦИЗМ) П. Мондриана (см. МОНДРИАН Пит)) сочетают рационализм с романтикой, тяготея к построению «абсолютных» красочно-графических монументальных символов, выражающих мистические законы космоса. В то же время геометрическая абстракция впитала в себя и технократический пафос конструктивизма (см. КОНСТРУКТИВИЗМ). Во второй половине 20 в. в таких течениях, как оп-арт (см. ОП-АРТ) и постживописная абстракция (см. ПОСТЖИВОПИСНАЯ АБСТРАКЦИЯ), геометрическая абстракция сохраняет свой «рационалистический мистицизм», еще теснее сближаясь с многообразной динамикой современной жизни.
ГЕОМЕТРИЧЕСКАЯ абстракция - один из видов абстрактного искусства, предпочитающий композиции, в основе которых - строгая ритмика геометрических или (в скульптуре) стереометрических фигур. Ее ранние варианты (отчасти орфизм Р. Делоне и Ф. Купки, а также супрематизм К. С. Малевича и неопластицизм П. Мондриана) сочетают рационализм с романтикой, тяготея к построению "абсолютных" красочно-графических монументальных символов, выражающих мистические законы космоса. В то же время геометрическая абстракция впитала в себя и технократический пафос конструктивизма. Во второй половине 20 в. в таких течениях, как оп-арт и постживописная абстракция, геометрическая абстракция сохраняет свой "рационалистический мистицизм", еще теснее сближаясь с многообразной динамикой современной жизни.
Геометри́ческая изомери́я - то же, что цис-транс-изомерия.
* * *
ГЕОМЕТРИЧЕСКАЯ ИЗОМЕРИЯ - ГЕОМЕТРИ́ЧЕСКАЯ ИЗОМЕРИ́Я, то же, что цис-транс-изомерия (см. ЦИС-ТРАНС-ИЗОМЕРИЯ).
ГЕОМЕТРИЧЕСКАЯ ИЗОМЕРИЯ - то же, что цис-транс-изомерия.
Геометри́ческая о́птика - раздел оптики, в котором распространение света в прозрачных средах рассматривается на основе представления о световом луче как линии, вдоль которой распространяется световая энергия. Законы геометрической оптики применяются для расчётов построения изображения при прохождении света через оптические системы.
* * *
ГЕОМЕТРИЧЕСКАЯ ОПТИКА - ГЕОМЕТРИ́ЧЕСКАЯ О́ПТИКА, раздел оптики, в котором распространение света в прозрачных средах рассматривается на основе представления о световом луче как линии, вдоль которой распространяется световая энергия. Законы геометрической оптики применяются для расчетов построения изображения при прохождении света через оптические системы.
ГЕОМЕТРИЧЕСКАЯ ОПТИКА - раздел оптики, в котором распространение света в прозрачных средах рассматривается на основе представления о световом луче как линии, вдоль которой распространяется световая энергия. Законы геометрической оптики применяются для расчетов построения изображения при прохождении света через оптические системы.
ГЕОМЕТРИЧЕСКАЯ ОПТИКА, раздел оптики, в котором распространение света в прозрачных средах описывается с помощью представления о световых лучах, а волновые и квантовые свойства не учитываются. Основные законы геометрической оптики - отражения света и преломления света на границе раздела 2 однородных сред - в основном достаточны для построения изображений оптических в оптических системах, а также для описания аберраций и методов их исправления. По аналогии с геометрической оптикой применяется также понятие геометрическая акустики.
преломление. лучепреломление.
преломить, -ся.
аберрация. астигматизм. дисторсия. кома.
каустика, каустическая поверхность.
фокус. фокальный.
диоптрия.
диоптрика.
увеличительный (# линза). <-> уменьшительный.
менисковые системы.
гомоцентрический пучок лучей.
параксиальный.
виньетирование.
эйконал.
анаморфоз. анаморфирование. анаморфоты.
растр. растровая оптика.
катоптрика.
Геометри́ческая прогре́ссия - последовательность чисел, из которых каждое следующее получается из предыдущего умножением на постоянное число q, называемое знаменателем геометрической прогрессии, например 2, 8, 32, 128, ..., q = 4.
* * *
ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ - ГЕОМЕТРИ́ЧЕСКАЯ ПРОГРЕ́ССИЯ, последовательность чисел, из которых каждое следующее получается из предыдущего умножением на постоянное число q, называемого знаменателем геометрической прогрессии, напр., 2, 8, 32, 128,..., q = 4.
ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ - последовательность чисел, из которых каждое следующее получается из предыдущего умножением на постоянное число q, называемого знаменателем геометрической прогрессии, напр., 2, 8, 32, 128,..., q = 4.
ГЕОМЕТРИЧЕСКАЯ РЕЗЬБА ПО ДЕРЕВУ - ГЕОМЕТРИ́ЧЕСКАЯ РЕЗЬБА́ ПО ДЕ́РЕВУ, один из самых древних и распространенных видов деревянной орнаментальной резьбы. Выполняется в виде выемок двух-, трех-, четырехгранной формы, которые в сочетании дают большое число разнообразных композиций. Главный инструмент резчика - резец со скошенным концом, так называемый «косячок».
Геометрическая резьба подразделяется на две основные разновидности: трехгранно-выемчатая резьба и ногтевидная (или скобчатая).
В основе первой лежит заглубленная внутрь трехгранная пирамидка, из которой формируются разнообразные орнаменты. Ногтевидная резьба получила свое название от полукруглого углубления - «ноготка», наносимого полукруглой стамеской. Сочетания «ноготков» дают более сложные узоры - листики, трилистники, глазки.
Орнаментика геометрической резьбы восходит к древним языческим символам. Например, один из наиболее распространенных элементов - розетка - был связан с культом солнца. Розетки и сияния присутствуют во всех композициях, выполненных в технике трехгранно-выемчатой резьбы. Геометрическая резьба использовалась в домовом декоре Русского Севера и при украшении прялок (см. ПРЯЛКА) и различных предметов домашней утвари - вальков, рубелей, трепал. Геометрический узор встречается на предметах из новгородских раскопок 10-12 веков. Подобные орнаменты украшают изделия западноевропейских ремесленников, мастеров Средней Азии.
В конце 19 века, на гребне волны интереса к народному искусству, геометрическую резьбу вновь начинают широко применять в архитектуре, при оформлении мебели и деталей интерьера. Эту технику использовали столярные мастерские в Талашкине (см. ТАЛАШКИНО), Абрамцеве (см. АБРАМЦЕВО), Нижнем Новгороде, эскизы для орнамента делали профессиональные художники. Сегодня геометрическая резьба применяется главным образом при отделке мелких бытовых предметов и в сувенирном производстве.
нареч. качеств.-обстоят.
1. В соответствии с законами и принципами геометрии [геометрия I 1.] как раздела математики, изучающего пространственные отношения и формы.
2. Геометрическим способом.
Геометри́чески неизменя́емая систе́ма (в строительной механике), система соединённых между собой тел (например, стержней, дисков), изменение формы которых невозможно без деформации материала. Все несущие конструкции зданий и сооружений являются геометрически неизменяемыми системами.
* * *
ГЕОМЕТРИЧЕСКИ НЕИЗМЕНЯЕМАЯ СИСТЕМА - ГЕОМЕТРИ́ЧЕСКИ НЕИЗМЕНЯ́ЕМАЯ СИСТЕ́МА, в строительной механике - система соединенных между собой тел (напр., стержней, дисков), изменение формы которых невозможно без деформации материала. Все несущие конструкции зданий и сооружений являются геометрически неизменяемыми системами.
ГЕОМЕТРИЧЕСКИ НЕИЗМЕНЯЕМАЯ система - в строительной механике - система соединенных между собой тел (напр., стержней, дисков), изменение формы которых невозможно без деформации материала. Все несущие конструкции зданий и сооружений являются геометрически неизменяемыми системами.
Геометри́ческие построе́ния - приёмы, позволяющие по графически данным элементам (точкам, прямым, окружностям) найти (построить) с помощью наперёд заданных средств другие элементы, связанные с данными некоторыми условиями. Наиболее известны построения с помощью циркуля и линейки (односторонней, без делений). В связи с этим типом геометрических построений возникли классические задачи древности: квадратура круга, трисекция угла и удвоение куба.
* * *
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ - ГЕОМЕТРИ́ЧЕСКИЕ ПОСТРОЕ́НИЯ, приемы, позволяющие по графически данным элементам (точкам, прямым, окружностям) найти (построить) с помощью наперед заданных средств другие элементы, связанные с данными некоторыми условиями. Наиболее известны построения с помощью циркуля и линейки (односторонней, без делений). В связи с этим типом геометрических построений возникли классические задачи древности: квадратура круга (см. КВАДРАТУРА КРУГА), трисекция угла и удвоение куба (см. УДВОЕНИЕ КУБА).
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ - приемы, позволяющие по графически данным элементам (точкам, прямым, окружностям) найти (построить) с помощью наперед заданных средств другие элементы, связанные с данными некоторыми условиями. Наиболее известны построения с помощью циркуля и линейки (односторонней, без делений). В связи с этим типом геометрических построений возникли классические задачи древности: квадратура круга, трисекция угла и удвоение куба.
прил.
1. соотн. с сущ. геометрия I 1., связанный с ним
2. Свойственный геометрии [геометрия I 1.], характерный для неё.
3. Образованный линиями и схематическими фигурами (треугольниками, окружностями, прямоугольниками и т.п.).
ГЕОМЕТРИ́ЧЕСКИЙ, геометрическая, геометрическое (научн.).
1. прил. к геометрия. Геометрическая теорема. Геометрические тела (шар, конус, пирамида, призма и др.). Геометрические фигуры (треугольник, квадрат, круг и др.).
2. Состоящий из линий, точек, геометрических фигур (спец.). Геометрический орнамент. Геометрический стиль. Геометрическая резьба.
ГЕОМЕТРИ́ЧЕСКИЙ -ая, -ое.
1. к Геоме́трия. Г-ая задача. Г-ая аксиома. Г-ая теорема. Г-ое понятие. Г-ая прогрессия.
2. Состоящий из линий, точек и схематических фигур (треугольников, конусов, кривых и т.п.). Г. орнамент.
◁ Геометри́чески, нареч. Г. расчерченные дорожки. Г. точно проложить улицы.
-ая, -ое.
1. прил. к геометрия.
Геометрическая задача. Геометрическая
аксиома. Геометрический метод.
2. Состоящий из линий, точек и схематических фигур (треугольников, конусов, кривых и т. п.).
Геометрический орнамент.
геометри́ческий, геометри́ческая, геометри́ческое, геометри́ческие, геометри́ческого, геометри́ческой, геометри́ческих, геометри́ческому, геометри́ческим, геометри́ческую, геометри́ческою, геометри́ческими, геометри́ческом, геометри́ческ, геометри́ческа, геометри́ческо, геометри́чески